[논문리뷰] Grounding Image Matching in 3D with MASt3R

arXiv 2024. [Paper] [Page] [Github]
Vincent Leroy, Yohann Cabon, Jérôme Revaud
Naver Labs Europe
14 Jun 2024

DUSt3R의 후속 논문

Introduction

본 논문에서는 DUSt3R가 실제로 매칭에 사용될 수 있지만, 시점 변화에 매우 robust함에도 불구하고 비교적 부정확하다는 점을 지적하였다. 이를 해결하기 위해, 저자들은 dense한 로컬 feature map을 예측하는 두 번째 head를 부착하고 infoNCE loss로 학습시키는 것을 제안하였다. 그 결과, 새로운 아키텍처인 MASt3R (Matching And Stereo 3D Reconstruction)는 여러 벤치마크에서 DUSt3R보다 성능이 뛰어나다.

저자들은 픽셀 정확도의 매칭을 얻기 위해, 여러 스케일에서 매칭을 수행하는 coarse-to-fine matching 방식을 제안하였다. 각 매칭 단계에는 dense feature map에서 reciprocal match들을 추출하는 것이 포함되는데, 이는 dense feature map 자체를 계산하는 것보다 훨씬 더 많은 시간이 소요된다. 저자들은 reciprocal match들을 찾는 더 빠른 알고리즘을 제안하였으며, 포즈 추정 품질을 개선하는 동시에 거의 100배 더 빠르다.

reciprocal match: 두 이미지 간의 feature point 매칭에서 상호 일치하는 대응점

Method

카메라 파라미터를 모르는 두 카메라로 촬영한 두 이미지 $I^1$과 $I^2$가 주어졌을 때, 픽셀 correspondence의 집합 \(\{(i, j)\}\)을 복구하고자 한다. 단순성을 위해 해상도가 같다고 가정하지만 해상도가 달라도 상관없으며, 최종 네트워크는 여러 종횡비 쌍을 처리할 수 있다.

1. The DUSt3R framework

DUSt3R는 이미지만으로 calibration과 3D 재구성 문제를 함께 해결하는 접근 방식이다. 두 개의 입력 이미지가 주어졌을 때, transformer 기반 네트워크는 로컬 3D 재구성을 예측하는데, 이는 두 개의 dense한 3D 포인트 클라우드 $X^{1,1}$과 $X^{2,1}$의 형태이며, 이를 pointmap이라 부른다.

Pointmap $X^{a,b} \in \mathbb{R}^{H \times W \times 3}$은 이미지 $I^a$의 각 픽셀 $i = (u, v)$와 카메라 $b$의 좌표계에서 표현된 3D 포인트 $X_{u,v}^{a,b} \in \mathbb{R}^3$ 사이의 dense한 2D-3D 매핑을 나타낸다. DUSt3R는 첫 번째 카메라의 좌표계에서 표현된 두 pointmap $X^{1,1}$과 $X^{2,1}$을 예측함으로써 calibration과 3D 재구성 문제를 동시에 효과적으로 해결한다.

세 개 이상의 이미지가 제공되는 경우, 추가로 global alignment를 통해 동일한 좌표계로 모든 pointmap을 병합한다. 본 논문에서 이 단계를 사용하지 않고 두 개의 이미지가 주어지는 경우로 제한하였다.

두 이미지는 모두 ViT를 사용하여 샴 방식으로 먼저 인코딩되어 두 가지 표현 $H^1$과 $H^2$가 생성된다.

\[\begin{aligned} H^1 &= \textrm{Encoder} (I^1) \\ H^2 &= \textrm{Encoder} (I^2) \end{aligned}\]

그런 다음, 두 개의 얽힌 디코더가 이러한 표현을 공동으로 처리하며, cross-attention을 통해 정보를 교환하여 시점과 장면의 글로벌 3D 형상 간의 공간적 관계를 이해한다. 이 공간 정보로 증강된 새로운 표현을 $H^{\prime 1}$과 $H^{\prime 2}$라 하자.

\[\begin{equation} H^{\prime 1}, H^{\prime 2} = \textrm{Decoder} (H^1, H^2) \end{equation}\]

마지막으로, 두 개의 예측 head는 인코더와 디코더에서 출력된 표현들을 concat해서 최종 pointmap과 신뢰도 맵을 예측한다.

\[\begin{aligned} X^{1,1}, C^1 &= \textrm{Head}_\textrm{3D}^1 ([H^1, H^{\prime 1}]) \\ X^{2,1}, C^2 &= \textrm{Head}_\textrm{3D}^2 ([H^2, H^{\prime 2}]) \end{aligned}\]

Regression loss

DUSt3R는 간단한 regression loss를 사용하여 fully-supervised 방식으로 학습된다.

\[\begin{equation} \ell_\textrm{regr} (v,i) = \| \frac{1}{z} X_i^{v,1} - \frac{1}{\hat{z}} \hat{X}_i^{v,1} \| \end{equation}\]

(\(v \in \{1, 2\}\)는 뷰, $i$는 GT 3D 포인트 $\hat{X}^{v,1} \in \mathbb{R}^3$이 정의된 픽셀)

원래 공식에서 정규화 factor $z$와 $\hat{z}$가 도입되어 재구성이 스케일에 불변하게 된다. $z$와 $\hat{z}$는 단순히 모든 유효한 3D 포인트에서 원점까지의 평균 거리로 정의된다.

Metric predictions

일부 경우에는 metric 스케일을 예측해야 하기 때문에, 스케일 불변성이 반드시 바람직한 것은 아니다. 따라서 저자들은 실제 pointmap이 metric으로 알려져 있을 때 예측된 pointmap에 대한 정규화를 무시하도록 regression loss를 수정하였다. 즉, 실제 pointmap이 metric일 때마다 $z = \hat{z}$로 설정하여 이 경우

\[\begin{equation} \ell_\textrm{regr} (v,i) = \frac{1}{\hat{z}} \| X_i^{v,1} - \hat{X}_i^{v,1} \| \end{equation}\]

가 된다. DUSt3R에서와 같이 최종 confidence-aware regression loss는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{conf} = \sum_{v \in \{1,2\}} \sum_{i \in \mathcal{V}^v} C_i^v \ell_\textrm{regr} (v,i) - \alpha \log C_i^v \end{equation}\]

2. Matching prediction head and loss

Pointmap에서 신뢰할 수 있는 픽셀 correspondence를 얻기 위한 표준 방법은 feature space에서 reciprocal match를 찾는 것이다. 이러한 방식은 극단적인 시점 변화가 있는 경우에도 DUSt3R가 예측한 pointmap에서 놀라울 정도로 잘 작동하지만, 결과 correspondence가 다소 부정확하여 최적이 아닌 정확도를 제공한다. 이는 regression이 본질적으로 노이즈의 영향을 받고 DUSt3R가 매칭을 찾기 위해 명시적으로 학습되지 않았기 때문에 당연한 결과이다.

Matching head

이러한 이유로 저자들은 두 개의 dense feature map $D^1, D^2 \in \mathbb{R}^{H \times W \times d}$를 출력하는 두 번째 head를 추가하는 것을 제안하였다.

\[\begin{aligned} D^1 &= \textrm{Head}_\textrm{desc}^1 ([H^1, H^{\prime 1}]) \\ D^2 &= \textrm{Head}_\textrm{desc}^2 ([H^2, H^{\prime 2}]) \end{aligned}\]

Head는 GELU activation function을 끼워 넣은 간단한 2-layer MLP로 구현된다. 마지막으로, 각 로컬 feature를 unit norm으로 정규화한다.

Matching objective

한 이미지의 각 local descriptor가 장면에서 같은 3D 포인트를 나타내는 다른 이미지의 descriptor와 일치하도록 장려하고자 한다. 이를 위해 GT correspondence \(\hat{\mathcal{M}} = \{(i,j) \vert \hat{X}_i^{1,1} = \hat{X}_j^{2,1}\}\)에 대한 infoNCE loss를 활용한다.

\[\begin{equation} \mathcal{L}_\textrm{match} = - \sum_{(i,j) \in \hat{\mathcal{M}}} \log \frac{s_\tau (i,j)}{\sum_{k \in \mathcal{P}^1} s_\tau (k,j)} + \log \frac{s_\tau (i,j)}{\sum_{k \in \mathcal{P}^2} s_\tau (i,k)} \\ \textrm{where} \quad s_\tau (i,j) = \exp (-\tau D_i^{1 \top} D_j^2), \; \mathcal{P}^1 = \{i \vert (i,j) \in \hat{\mathcal{M}}\}, \; \mathcal{P}^2 = \{j \vert (i,j) \in \hat{\mathcal{M}}\} \end{equation}\]

($\tau$는 temperature hyperparameter)

이 matching loss는 본질적으로 cross-entropy classification loss이다. Regression loss와 달리 네트워크는 근처 픽셀이 아닌 올바른 픽셀을 올바르게 얻는 경우에만 보상을 받는다. 이는 네트워크가 고정밀 매칭을 달성하도록 강력히 장려한다. 마지막으로 regression loss와 matching loss를 모두 결합하여 최종 학습 loss를 얻는다.

\[\begin{equation} \mathcal{L}_\textrm{total} = \mathcal{L}_\textrm{conf} + \beta \mathcal{L}_\textrm{match} \end{equation}\]

3. Fast reciprocal matching

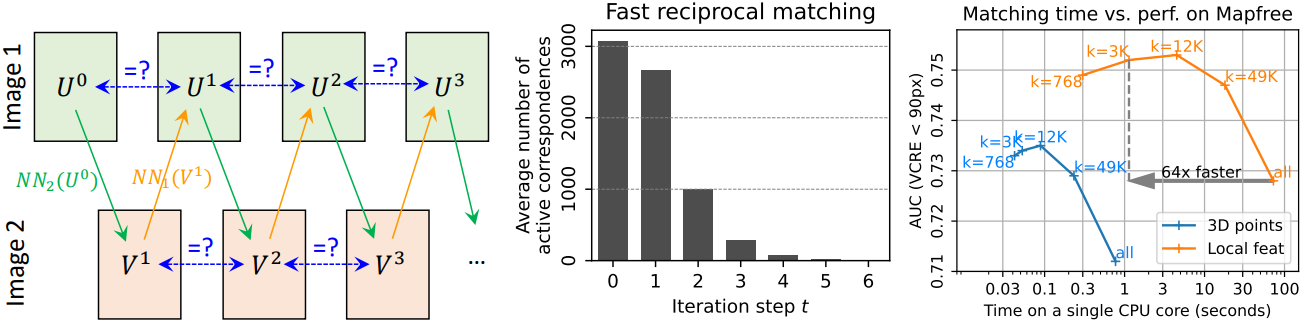
두 개의 예측된 feature map $D^1$과 $D^2$가 주어졌을 때, 서로의 상호 nearest neighbor, 즉 신뢰할 수 있는 픽셀 correspondence를 추출하는 것을 목표로 한다.

\[\begin{equation} \mathcal{M} = \{(i,j) \, \vert \, j = \textrm{NN}_2 (D_i^1), i = \textrm{NN}_1 (D_j^2)\} \\ \textrm{where} \quad \textrm{NN}_A (D_j^B) = \underset{i}{\arg \min} \| D_i^A - D_j^B \| \end{equation}\]

불행히도, reciprocal matching의 단순한 구현은 이미지의 모든 픽셀을 다른 이미지의 모든 픽셀과 비교해야 하기 때문에 $\mathcal{O}(W^2 H^2)$의 높은 계산 복잡도를 갖는다. Nearest-neighbor (NN) search를 최적화하는 것은 가능하지만, 이러한 종류의 최적화는 일반적으로 고차원 feature space에서 매우 비효율적이며 모든 경우에서 MASt3R이 $D^1$과 $D^2$를 출력하는 시간보다 수십 배 더 느리다.

Fast matching

따라서 저자들은 서브샘플링을 기반으로 한 더 빠른 접근 방식을 제안하였다. 이는 일반적으로 첫 번째 이미지 $I^1$의 그리드에서 정기적으로 샘플링되는 초기 $k$개의 픽셀 집합 \(U^0 = \{U_n^0\}_{n=1}^k\)에서 시작하는 반복 프로세스를 기반으로 한다. 그런 다음, 각 픽셀은 $I^2$의 NN에 매핑되어 $V^1$이 생성되고 결과 픽셀은 동일한 방식으로 $I^1$에 다시 매핑된다.

\[\begin{equation} U^t \mapsto [\textrm{NN}_2 (D_u^1)]_{u \in U^t} = V^t \mapsto [\textrm{NN}_1 (D_v^2)]_{v \in V^t} = U^{t+1} \end{equation}\]

그런 다음 reciprocal match들의 집합 \(\mathcal{M}_k^t = \{(U_n^t, V_n^t) \, \vert \, U_n^t = U_n^{t+1}\}\)을 수집한다. 다음 iteration에서는 이미 수렴한 픽셀을 필터링하여 제거한다.

\[\begin{equation} U^{t+1} := U^{t+1} \setminus U^t \end{equation}\]

마찬가지로 $t=1$에서 시작하여 $V^{t+1}$도 검증하고 필터링하여 비슷한 방식으로 $V^t$와 비교한다. 이 프로세스는 대부분의 대응이 안정된 쌍으로 수렴할 때까지 고정된 횟수만큼 반복된다. 수렴되지 않은 점의 수는 몇 번의 iteration 후 빠르게 0으로 감소한다. 마지막으로, 출력 correspondence 세트는 모든 \(\mathcal{M}_k^t\)을 concat하여 구성한다.

\[\begin{equation} \mathcal{M}_k = \cup_t \mathcal{M}_k^t \end{equation}\]

Theoretical guarantees

Fast matching의 전체 복잡도는 $\mathcal{O}(kWH)$이며, naive한 접근 방식보다 $WH/k \gg 1$배 더 빠르다. Fast matching 알고리즘은 전체 집합 $\mathcal{M}$의 부분 집합을 추출하는데, 이 부분 집합의 크기가 \(\vert \mathcal{M}_k \vert \le k\)로 제한된다.

4. Coarse-to-fine matching

입력 이미지 영역($W \times H$)에 대한 attention의 2차 복잡도로 인해 MASt3R는 긴 쪽이 512픽셀인 이미지만 처리한다. 더 큰 이미지는 학습하는 데 상당히 더 많은 컴퓨팅 파워가 필요하고 ViT는 아직 더 큰 해상도로 일반화되지 않았다. 결과적으로 고해상도 이미지는 축소해서 사용해야 하며, 그 후 결과 correspondence는 원래 이미지 해상도로 다시 확대된다. 이로 인해 성능 손실이 발생할 수 있으며, 때로는 위치 정확도 또는 재구성 품질 측면에서 상당한 저하를 일으킬 수 있다.

Coarse-to-fine matching은 저해상도 알고리즘으로 고해상도 이미지를 매칭하는 이점을 보존하기 위한 기술이다. 따라서 저자들은 MASt3R에 대한 이 아이디어를 탐구하였다.

1. 두 이미지의 축소된 버전에서 매칭을 수행한다. $k$개를 서브샘플링하여 얻은 coarse correspondence들의 집합을 \(\mathcal{M}_k^0\)이라 하자.
2. 각 전체 해상도 이미지에서 독립적으로 window crop의 그리드 $W^1, W^2 \in \mathbb{R}^{w \times 4}$를 생성한다. 각 window crop은 긴 쪽의 크기가 512이고, 인접한 window는 50% 겹친다.
3. 모든 window 쌍의 집합 $(w_1, w_2) \in W^1 \times W^2$에 대하여, \(\mathcal{M}_k^0\)의 대부분을 포함하는 부분 집합을 선택한다. 구체적으로, 90%의 correspondence를 포함할 때까지 greedy 방식으로 window 쌍을 하나씩 추가한다.

4. 각 window 쌍에 대해 독립적으로 매칭을 수행한다.

   \[\begin{aligned} D^{w_1}, D^{w_2} &= \textrm{MASt3R} (I_{w_1}^1, I_{w_2}^2) \\ \mathcal{M}_k^{w_1, w_2} &= \textrm{fast_reciprocal_NN} (D^{w_1}, D^{w_2}) \end{aligned}\]
5. 각 window 쌍에서 얻은 correspondence는 최종적으로 원본 이미지 좌표로 다시 매핑된 후 concat된다.

Experiments

• 데이터셋: Habitat, ARKitScenes, Blended MVS, MegaDepth, Static Scenes 3D, ScanNet++, CO3D-v2, Waymo, Mapfree, WildRgb, VirtualKitti, Unreal4K, TartanAir, 내부 데이터셋
• 학습 디테일
  • DUSt3R와 동일한 backbone 사용 (ViT-Large 인코더, ViT-Base 디코더더)
  • DUSt3R의 checkpoint로 가중치를 초기화
  • epoch: 35
  • learning rate: 0.0001 (cosine schedule)
  • DUSt3R와 동일하게 학습 이미지의 종횡비를 랜덤하게 선택 (긴 쪽의 크기가 512)
  • feature 차원: $d$ = 24
  • matching loss 가중치: $\beta$ = 1.0
  • matching loss 계산을 위한 GT는 이미지 쌍마다 4,096개의 correspondence를 샘플링

1. Map-free localization

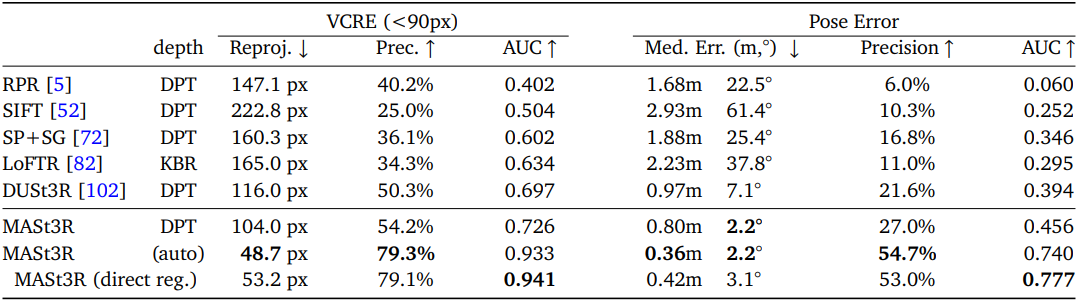
다음은 Map-free 데이터셋의 validation set에 대한 ablation 결과이다.

다음은 Map-free 데이터셋의 test set에 대한 SOTA와의 비교 결과이다.

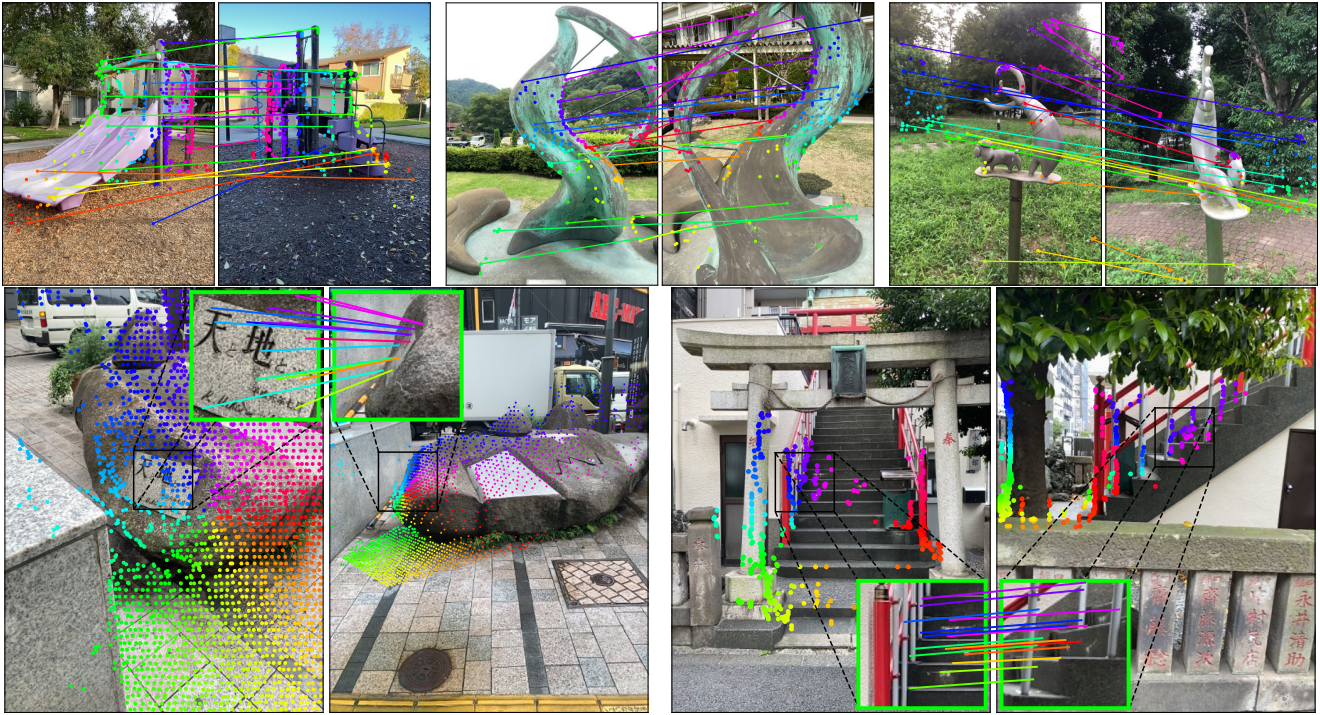
다음은 Map-free에서의 매칭 예시들이다.

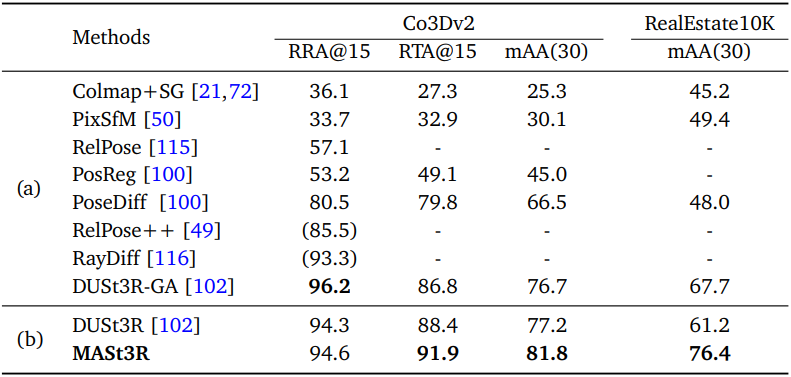
2. Relative pose estimation

다음은 CO3Dv2와 RealEstate10K에서의 멀티뷰 포즈 추정 성능을 비교한 표이다.

3. Visual localization

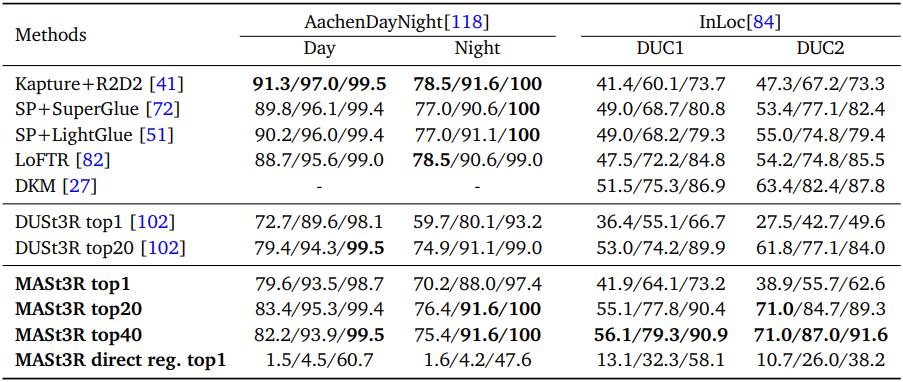
다음은 Aachen Day-Night과 InLoc에서의 visual localization 성능을 비교한 표이다.

다음은 Aachen Day-Night에서의 매칭 예시들이다.

다음은 InLoc에서의 매칭 예시들이다.

4. Multiview 3D reconstruction

다음은 DTU에서의 MVS 성능을 비교한 표이다.

다음은 DTU에서의 MVS 결과들이다.