[논문리뷰] Fast Training of Diffusion Models with Masked Transformers (MaskDiT)

arXiv 2023. [Paper] [Github]
Hongkai Zheng, Weili Nie, Arash Vahdat, Anima Anandkumar
NVIDIA | Caltech
15 Jun 2023

Introduction

Diffusion model은 특히 텍스트 입력으로 고품질의 다양한 이미지를 합성할 때 우수한 이미지 생성 성능으로 인해 가장 인기 있는 심층 생성 모델 클래스가 되었다. Diffusion model의 대규모 학습은 사실적인 이미지와 창의적인 예술을 생성하는 능력에 필수적이다. 그러나 diffusion model을 교육하려면 많은 양의 컴퓨팅 리소스와 시간이 필요하며, 이는 모델을 추가로 확장하는 데 있어 주요 한계점으로 남아 있다. 예를 들어 오리지널 Stable Diffusion은 256개의 A100 GPU에서 24일 이상 학습되었다. 인프라와 구현이 개선되면서 256개의 A100 GPU에서 학습 비용을 13일로 줄일 수 있지만 대부분의 연구자와 실무자는 여전히 접근할 수 없다. 따라서 diffusion model의 학습 효율성을 개선하는 것은 여전히 해결해야 할 문제이다.

Masked Training은 자연어 처리, 컴퓨터 비전, 시각 언어 이해와 같은 도메인에서 학습 효율성을 향상시키기 위해 널리 사용되었다. 마스킹된 학습은 특히 비전 애플리케이션에서 전체 학습 시간과 메모리를 크게 줄인다. 또한 masked training은 시각적 모양의 높은 중복으로 인해 모델이 마스킹되지 않은 패치에서 학습할 수 있으므로 representation learning 품질을 희생하지 않는 효과적인 self-supervised 기술이다. 여기에서 masked training은 패치에서 작동하기 때문에 transformer 아키텍처에 크게 의존하며 그 중 일부를 마스킹하는 것은 당연하다.

그러나 현재 diffusion model이 대부분 U-Net을 표준 네트워크 backbone으로 사용하기 때문에 masked training을 diffusion model에 직접 적용할 수 없다. U-Net의 convolution은 일반 고밀도 그리드에서 작동하므로 마스킹된 토큰을 통합하고 입력 패치의 랜덤 부분 집합으로 학습하는 것이 어렵다. 따라서 masked training 기법을 U-Net 모델에 적용하는 것은 간단하지 않다.

최근 몇 가지 연구들에서 diffusion model의 backbone으로 U-Net 아키텍처를 Vision Transformer (ViT)로 대체하면 표준 이미지 생성 벤치마크에서 유사하거나 더 나은 성능을 달성할 수 있음을 보여주었다. 특히 Diffusion Transformer (DiT)는 U-Net의 inductive bias에 의존하지 않고 ViT의 좋은 사례들을 계승하여 diffusion model에 대한 DiT backbone의 확장성을 보여주었다. 이는 대형 transformer 기반 diffusion model의 효율적인 학습을 위한 새로운 기회를 열어주었다. 그러나 표준 ViT와 유사하게 DiT 학습은 계산 비용이 많이 들고 수백만 번의 iteration이 필요하다. 최근 연구에서는 생성 성능을 개선하기 위해 DiT에 마스킹을 도입했지만 학습 중에 마스킹된 토큰과 완전한 토큰을 모두 인코딩하기 때문에 최대 용량 아키텍처의 학습 효율성을 개선하지 않았다. 실제로 step당 계산 및 메모리 비용은 원래 DiT보다 높다.

본 논문에서는 DiT의 transformer 구조를 활용하여 훨씬 더 빠르고 저렴한 학습을 위해 마스킹된 모델링을 활성화한다. 주요 가설은 이미지가 픽셀 space에 상당한 중복성을 포함한다는 것이다. 따라서 픽셀의 부분 집합에서 denoising score matching (DSM) loss를 최소화하여 diffusion model을 학습할 수 있다. Masked training에는 두 가지 주요 이점이 있다.

1. 이미지 패치의 부분 집합에 대해서만 학습할 수 있으므로 iteration당 계산 비용이 크게 줄어든다.
2. 특히 제한된 데이터 설정에서 학습 성능을 향상시킬 수 있는 여러 view로 학습 데이터를 보강할 수 있다.

본 논문은 이 가설에 따라 Masked Diffusion Transformer (MaskDiT)라고 하는 대형 transformer 기반 diffusion model을 학습시키는 효율적인 접근 방식을 제안한다. 먼저 transformer 인코더가 마스킹되지 않은 패치에서만 작동하고 가벼운 transformer 디코더가 전체 패치 세트에서 작동하는 비대칭 인코더-디코더 아키텍처를 채택한다. 그런 다음 두 부분으로 구성된 새로운 목적 함수를 설계한다.

1. DSM loss를 통해 마스킹되지 않은 패치의 score를 예측
2. 평균 제곱 오차(MSE) loss를 통해 입력의 마스킹된 패치를 재구성

이는 diffusion model이 마스킹되지 않은 패치에 overfitting되는 것을 방지하는 전체 이미지에 대한 글로벌한 지식을 제공한다. 단순화를 위해 학습 중 모든 diffusion timestep에 동일한 마스킹 비율 (ex. 50%)을 적용한다. 학습 후에는 학습과 inference 사이의 분포 격차를 줄이기 위해 마스킹 없이 모델을 fine-tuning하며 이로 인해 최소한의 오버헤드만 발생시킨다 (총 학습 비용의 6% 미만).

학습 이미지의 50% 패치를 무작위로 제거함으로써 iteration당 학습 비용을 2배로 줄인다. 본 논문이 제안한 새로운 아키텍처와 새로운 목적 함수를 통해 MaskDiT는 더 적은 학습 step으로 DiT와 유사한 성능을 달성할 수 있으므로 전체 학습 비용이 훨씬 더 적다. 클래스 조건부 ImageNet-256$\times$256 생성 벤치마크에서 MaskDiT는 guidance 없이 5.69의 FID를 달성하여 이전 diffusion model을 능가하고 guidance로 2.28의 FID를 달성하여 SOTA 방법들과 비슷한 성능을 보인다. FID 2.28의 결과를 달성하기 위해 MaskDiT 학습은 8개의 A100 GPU에서 273시간이 소요되며 이는 DiT 학습 시간의 31%에 불과하다.

Method

1. Preliminaries

Diffusion model

본 논문은 Score-based generative modeling through stochastic differential equations 논문을 따라 연속 시간 설정에서 forward process와 reverse process를 도입한다. Forward process에서 diffusion model은 SDE를 통해 실제 데이터 $x_0 \sim p_\textrm{data} (x_0)$를 noise 분포 \(x_T \sim \mathcal{N}(0, \sigma_\textrm{max}^2 I)\)로 diffuse한다.

\[\begin{equation} dx = f(x, t)dt + g(t) dw \end{equation}\]

여기서 $f$는 drift coefficient, $g$는 diffusion coefficient, $w$는 표준 Wiener process이며, 시간 $t$는 0에서 $T$로 흐른다. Reverse process에서는 다음과 같은 SDE로 샘플 생성이 가능하다.

\[\begin{equation} dx = [f(x, t) - g(t)^2 \nabla_x \log p_t (x)] dt + g(t) d \bar{w} \end{equation}\]

여기서 $\bar{w}$는 reverse-time Wiener process이다. 위의 reverse SDE는 probability flow ODE로 변환될 수 있다.

\[\begin{equation} dx = [f(x, t) - \frac{1}{2} g(t)^2 \nabla_x \log p_t (x)] dt \end{equation}\]

이 ODE는 모든 timestep $t$에서 SDE와 동일한 주변 분포를 가진다. 본 논문은 $f(x, t) := 0$, $g(t) := \sqrt{2t}$로 설정하여 EDM 공식을 따를 수 있다. 구체적으로, forward SDE는

\[\begin{equation} x = x_0 + n, \quad n \sim \mathcal{N}(0, t^2 I) \end{equation}\]

로 줄일 수 있으며, probability flow ODE는

\[\begin{equation} dx = -t \nabla_x \log p_t (x) dt \end{equation}\]

가 된다. Score function $s (x, t) := \nabla_x \log p_t (x)$를 학습하기 위해 EDM은 denoising function $D_\theta (x, t)$를 parameterize하여 다음과 같은 denoising score matching loss를 최소화한다.

\[\begin{equation} \mathbb{E}_{x_0 \sim p_\textrm{data}} \mathbb{E}_{n \sim \mathcal{N}(0, t^2 I)} \| D_\theta (x_0 + n, t) - x_0 \|^2 \end{equation}\]

그러면 추정된 score는 다음과 같다.

\[\begin{equation} \hat{s} (x, t) = \frac{D_\theta (x, t) - x}{t^2} \end{equation}\]

Classifier-free guidance

클래스 조건부 생성의 경우 classifier-free guidance (CFG)는 diffusion model의 생성 품질을 개선하기 위해 널리 사용되는 샘플링 방법이다. EDM 공식에서 클래스 조건부 denoising function을 $D_\theta (x, t, c)$로 표시하고, CFG는 수정된 denoising function을 정의한다.

\[\begin{equation} \hat{D}_\theta (x, t, c) = D_\theta (x, t) + w (D_\theta (x, t, c) − D_\theta (x, t)) \end{equation}\]

여기서 $w \ge 1$은 guidance scale이다. CFG 샘플링에 대한 unconditional model을 얻으려면 단순히 null 토큰 $\emptyset$을 사용하여 클래스 레이블 $c$를 대체할 수 있다.

\[\begin{equation} D_\theta(x, t) := D_\theta (x, t, \emptyset) \end{equation}\]

학습하는 동안 $c$를 고정 확률 \(p_\textrm{uncond}\)를 사용하여 null 토큰 $\emptyset$로 랜덤하게 설정한다.

2. Key designs

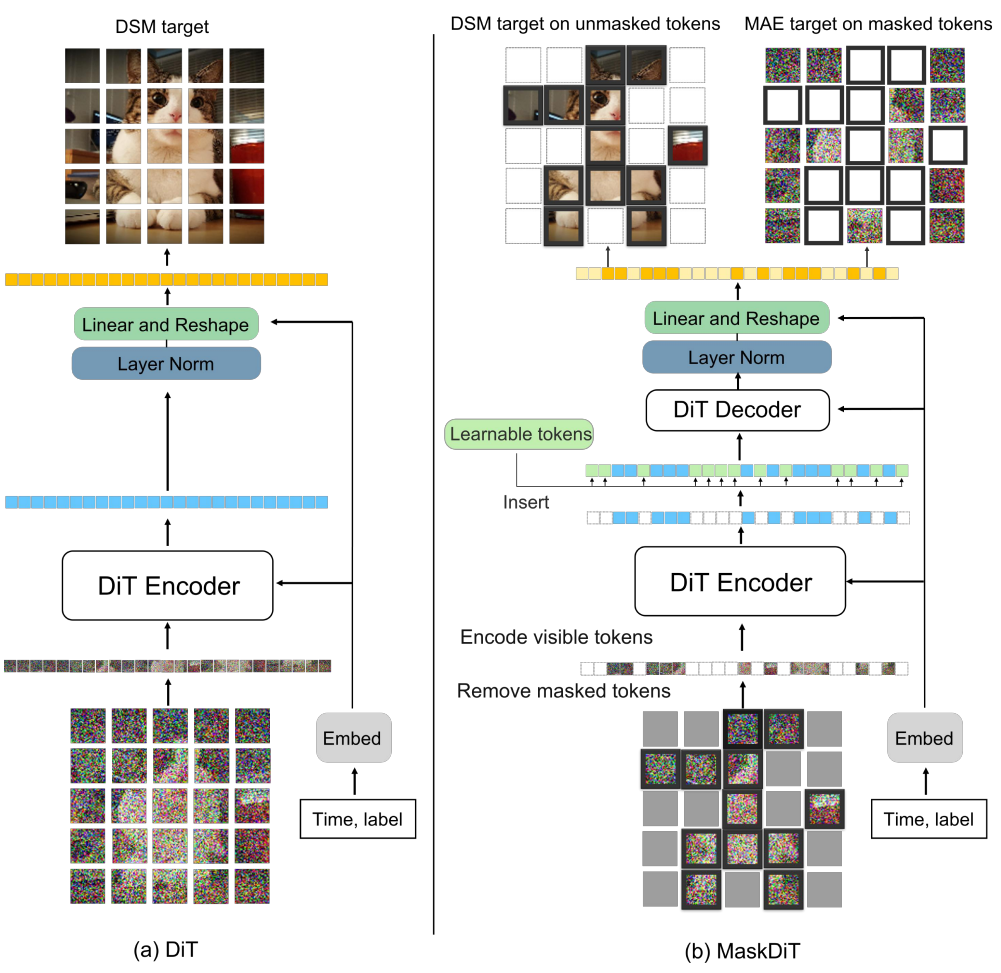
이미지 마스킹

깨끗한 이미지 $x_0$와 timestep $t$가 주어지면 먼저 Gaussian noise $n$을 추가하여 diffuse된 이미지 $x_t$를 얻는다. 그런 다음 $x_t$를 각각 패치 크기가 $p \times p$인 $N$개의 겹치지 않는 패치 그리드로 나눈다 (“patchify”). 해상도가 $H \times W$인 이미지의 경우

\[\begin{equation} N = \frac{HW}{p^2} \end{equation}\]

이다. 고정된 마스킹 비율 $r$을 사용하여 $\lfloor rN \rfloor$개의 패치를 랜덤하게 제거하고 나머지 $N − \lfloor rN \rfloor$개의 마스킹되지 않은 패치만 diffusion model에 전달한다. 단순화를 위해 모든 timestep에 대해 동일한 마스킹 비율 $r$을 유지한다. 높은 마스킹 비율은 계산 효율을 크게 향상시키지만 score 추정의 학습 신호를 감소시킬 수도 있다. $x_t$의 큰 중복성을 감안할 때 마스킹이 있는 학습 신호는 인접한 패치에서 마스킹된 패치를 외삽하는 모델의 능력로 보상될 수 있다. 따라서 좋은 성과와 높은 학습 효율성을 모두 달성하는 최적의 지점이 존재할 수 있다.

비대칭 인코더-디코더 backbone

Diffusion 백본은 diffusion model을 위한 표준 ViT 기반 아키텍처인 DiT를 기반으로 하며 약간의 수정이 있다. MAE와 유사하게 비대칭 인코더-디코더 아키텍처를 적용한다.

1. 인코더는 최종 linear projection layer가 없는 것을 제외하고 원래 DiT와 아키텍처가 동일하며 마스킹되지 않은 패치에서만 작동한다.
2. 디코더는 가벼운 MAE 디코더에서 채택된 또 다른 DiT 아키텍처이며 전체 토큰을 입력으로 사용한다.

DiT와 마찬가지로 인코더는 모든 입력 토큰에 추가된 표준 ViT 주파수 기반 위치 임베딩과 함께 linear projection으로 패치를 임베딩한다. 그런 다음 마스킹된 토큰은 나머지 인코더 레이어로 전달되기 전에 제거된다. 디코더는 새 마스크 토큰과 함께 인코딩된 마스킹되지 않은 토큰을 모두 입력으로 사용한다. 여기서 각 마스크 토큰은 학습 가능한 공유 벡터이다. 그런 다음 디코더에 전달하기 전에 모든 토큰에 동일한 위치 임베딩을 추가한다. 비대칭 디자인 (ex. DiT-XL/2의 파라미터가 9% 미만인 MAE 디코더)로 인해 마스킹은 iteration당 계산 비용을 크게 줄일 수 있다.

목적 함수

Diffusion model의 일반적인 학습과 달리 전체 토큰에 대해 denoising score matching을 수행하지 않는다. 이는 보이는 마스킹되지 않은 패치에만 의존하여 마스킹된 패치의 score를 예측하기 어렵기 때문이다. 대신 목적 함수를 두 가지 하위 task로 분해한다.

1. 마스킹되지 않은 토큰에 대한 score 추정 task
2. 마스킹된 토큰에 대한 보조 재구성 task

이진 마스킹 레이블을 \(m \in \{0, 1\}^N\)으로 표기하고, 교체 없이 $\lfloor rN \rfloor$개의 패치를 균일하게 샘플링하고 마스킹한다고 하자. 마스킹되지 않은 토큰의 denoising score matching loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{DSM} = \mathbb{E}_{x_0 \sim p_\textrm{data}, n \sim \mathcal{N}(0, t^2 I), m} \| (D_\theta ((x_0 + n) \odot (1 - m), t) - x_0) \odot (1 - m) \|^2 \end{equation}\]

여기서 $\odot$은 patchify된 이미지의 토큰 길이 차원으로의 element-wise 곱셈이며, $(x_0 + n) \odot (1 - m)$은 $D_\theta$가 마스킹되지 않은 토큰만 입력으로 취한다는 것을 나타낸다. MAE와 비슷하게 재구성 task는 마스킹된 토큰에서 MSE loss를 계산하여 수행된다.

\[\begin{equation} \mathcal{L}_\textrm{MAE} = \mathbb{E}_{x_0 \sim p_\textrm{data}, n \sim \mathcal{N}(0, t^2 I), m} \| (D_\theta ((x_0 + n) \odot (1 - m), t) - (x_0 + n)) \odot m \|^2 \end{equation}\]

여기서 목표는 마스킹된 각 패치의 픽셀 값을 예측하여 입력 $x_0 + n$을 재구성하는 것이다. 이 MAE 재구성 loss를 추가하면 masked transformer가 글로벌한 이미지를 전체적으로 이해하도록 촉진할 수 있다. 따라서 보이는 패치의 로컬한 부분 집합에 \(\mathcal{L}_\textrm{DSM}\)이 overfitting되는 것을 방지할 수 있다고 가정할 수 있다.

전체 목적 함수는 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{DSM} + \lambda \mathcal{L}_\textrm{MAE} \end{equation}\]

여기서 hyperparameter $\lambda$는 score 예측 loss와 MAE 재구성 loss 사이의 균형을 제어하며, $\lambda$가 너무 크면 표준 DSM 업데이트에서 학습을 벗어나도록 하므로 너무 클 수 없다.

Unmasking tuning

모델이 마스킹된 이미지에 대해 학습되지만 표준 클래스 조건부 설정에서 고품질의 전체 이미지를 생성하는 데 사용할 수 있다. 그러나 저자들은 masked training이 원래 DiT 학습보다 CFG 샘플링의 성능이 항상 더 나쁘다는 것을 관찰했다. Unconditional model (클래스 레이블 $c$를 null 토큰 $\emptyset$로 설정)은 클래스 정보에 의존하지 않고 부분적으로 보이는 토큰만으로 score를 예측하기 어렵기 때문이다.

학습과 inference 사이의 격차를 더 좁히기 위해 masked training 후 최소한의 추가 비용으로 더 작은 batch size와 learning rate를 사용하여 모델을 fine-tuning한다. 또한 저자들은 unmasking tuning 중에 두 가지 다른 마스킹 비율 schedule을 살펴보았다.

1. zero-ratio schedule: 모든 튜닝 step에서 마스킹 비율을 $r = 0$으로 설정
2. cosine-ratio schedule: 현재 step $i$와 전체 튜닝 step 수 $n_\textrm{tot}$에 대하여 \(r = 0.5 \cos^4 ( (\pi i)/(2 n_\textrm{tot}) )\)으로 설정

이 unmasking tuning 전략은 CFG 샘플링의 더 나은 성능을 위해 약간 더 많은 학습 비용을 사용한다.

Experiments

• 데이터셋: ImageNet 256$\times$256
• 모델 설정
  • DiT와 마찬가지로 LDM 프레임워크 사용
  • LDM의 오토인코더는 Stable Diffusion의 사전 학습된 VAE를 사용 (downsampling factor 8)
  • Diffusion model
    • 인코더: DiT-XL/2를 사용
    • 디코더: MAE와 동일한 아키텍처 사용, 시간 및 클래스 임베딩에 adaptive layer norm block 추가
• 학습 디테일
  • Optimizer: AdamW
  • Learning rate = $10^{-4}$, weight decay 없음, EMA decay = 0.9999
  • DIT와 동일한 초기화 전략 사용
  • 마스킹 비율 = 50%, $\lambda = 0.1$, \(p_\textrm{uncond} = 0.1\)
  • Batch size = 1024
  • Unmasking tuning: learning rate = $5 \times 10^{-4}$로 변경
  • 모든 학습은 8개의 A100 GPU와 80GB 메모리에서 진행

1. Training efficiency

다음은 ImageNet 256$\times$256에서 SOTA diffusion model과 생성 성능을 비교한 그래프이다.

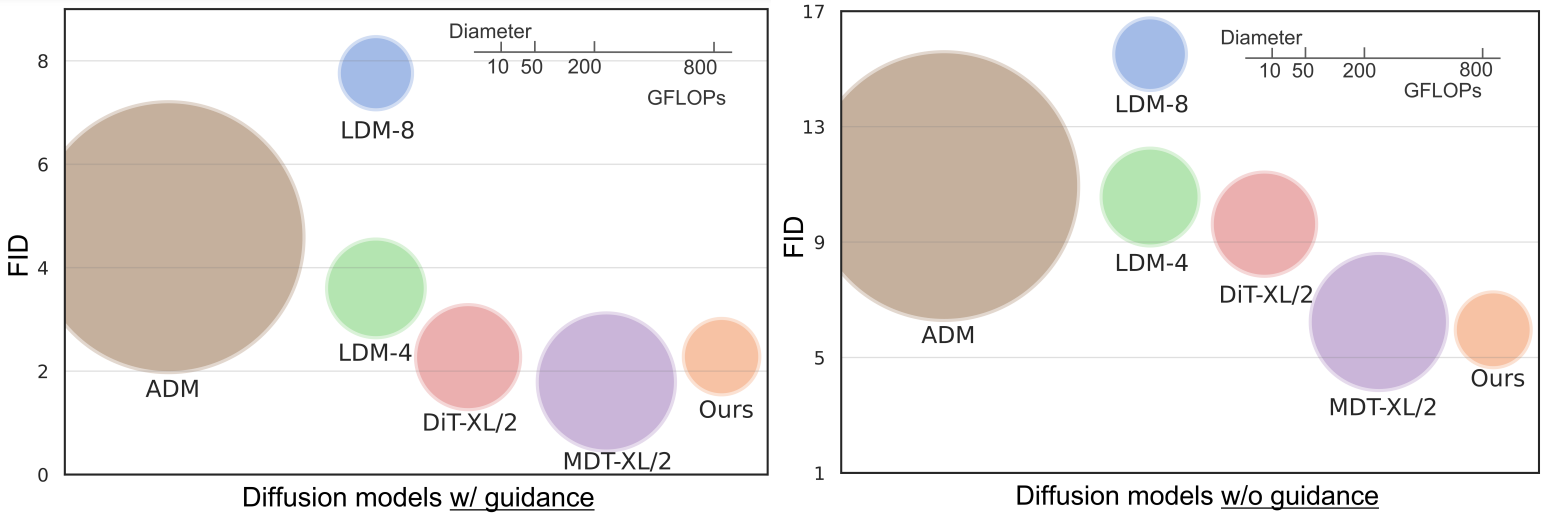
다음은 학습 시간과 GPU당 메모리 사용량을 비교한 그래프이다.

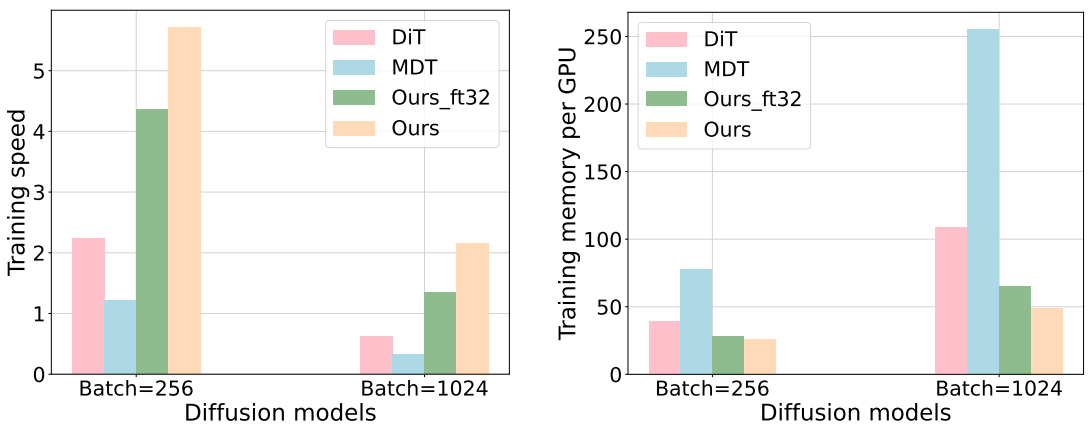
다음은 학습 시간에 따른 FID를 비교한 그래프이다.

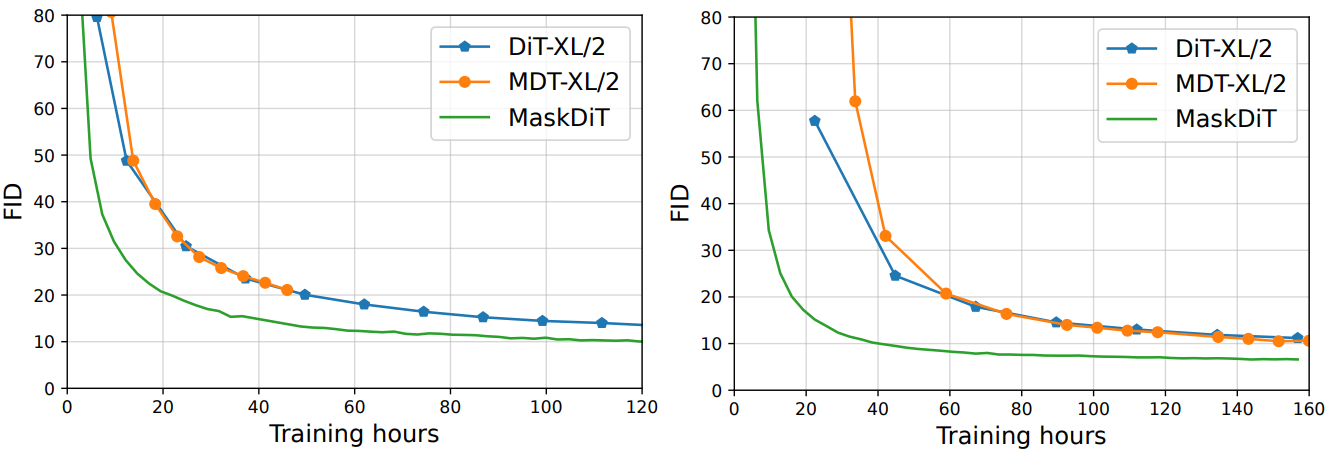
2. Comparison with state-of-the-art

다음은 클래스 조건부 ImageNet 256$\times$256에서 SOTA 모델들과 비교한 표이다.

다음은 MaskDiT로 생성한 샘플들이다. 위는 CFG를 사용하지 않은 샘플, 아래는 CFG ($w = 1.5$)를 사용한 샘플들이다.

3. Ablation studies

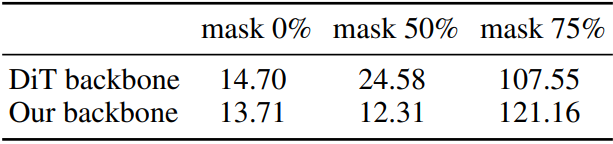
다음은 마스킹 비율과 diffusion backbone에 대한 영향을 나타낸 표이다.

다음은 MAE 재구성에 대한 영향을 나타낸 표이다.

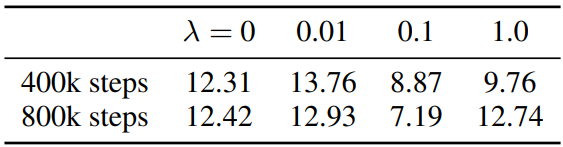
다음은 DSM 디자인에 대한 영향을 나타낸 표이다.

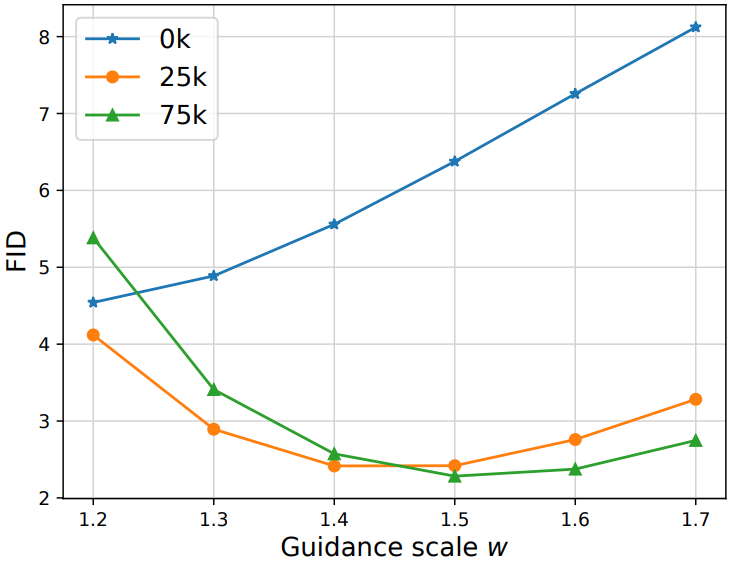
다음은 unmasking tuning step 수와 guidance scale $w$에 따른 FID을 나타낸 그래프이다.

Limitations

1. CFG를 사용할 때 SOTA FID를 달성하기 위해 여전히 몇 step의 unmasking tuning이 필요하다.
2. 좋은 unconditional diffusion model을 생성하지 못한다.
3. 제한된 계산 리소스로 인해 DiT-XL/2를 제외한 다른 diffusion transformer를 탐색하지 않았다.