[논문리뷰] Repurposing Diffusion-Based Image Generators for Monocular Depth Estimation (Marigold)

CVPR 2024 (Oral). [Paper] [Page] [Github]
Bingxin Ke, Anton Obukhov, Shengyu Huang, Nando Metzger, Rodrigo Caye Daudt, Konrad Schindler
ETH Zurich
4 Dec 2023

Introduction

Monocular depth estimation은 이미지를 depth map으로 변환하는 것, 즉 모든 픽셀의 범위 값을 회귀하는 것을 목표로 한다. 이 task는 3D 장면 구조가 필요할 때마다 사용되며 직접적인 범위나 스테레오 측정을 사용할 수 없다. 분명히 3D 세계에서 2D 이미지로의 projection을 undo하는 것은 기하학적으로 잘못된 문제이며 일반적인 객체 모양 및 크기, 장면 레이아웃, occlusion 패턴 등과 같은 사전 지식의 도움을 통해서만 해결될 수 있다. 즉, monocular depth에는 암시적으로 장면 이해가 필요하며, 딥러닝의 출현이 성능의 비약을 가져온 것은 우연이 아니다.

Depth estimation은 요즘 image-to-image translation으로 캐스팅되며 쌍을 이루고 잘 정렬된 RGB 및 깊이 이미지 컬렉션을 사용하여 supervised 방식으로 학습된다. 이러한 유형의 초기 방법은 학습 데이터에 의해 정의된 좁은 도메인, 주로 실내 또는 운전 장면으로 제한되었다.

최근에는 광범위한 장면에 걸쳐 기존 모델으로 사용하거나 소량의 데이터를 사용하여 특정 시나리오에 맞게 fine-tuning할 수 있는 일반적인 depth estimator를 학습시키는 연구가 진행되었다. 이러한 모델들은 일반적으로 MiDAS가 일반성을 달성하기 위해 처음 사용한 전략, 즉 여러 도메인의 다양한 RGB-D 데이터셋에서 샘플링한 데이터로 고용량 모델을 학습하는 전략을 따른다. 최근에는 convolution 인코더-디코더 네트워크에서 점점 더 크고 강력한 ViT로 이동했으며, 시각적 세계에 대한 더 많은 지식을 축적하고 결과적으로 더 나은 depth map을 생성하기 위해 점점 더 많은 데이터와 추가 task에 대한 학습이 포함되었다. 중요한 것은 깊이에 대한 시각적 단서는 장면 내용뿐만 아니라 일반적으로 모르는 camera intrinsics에 따라 달라진다. 일반적인 실제 depth estimation의 경우 affine-invariant depth(즉, 글로벌 오프셋 및 스케일까지의 깊이 값)를 추정하는 것이 선호되는 경우가 많다. 이는 “스케일 바” 역할을 할 수 있는 알려진 크기의 객체 없이도 결정할 수 있다.

최신 이미지 diffusion model은 특히 다양한 도메인에 걸쳐 고품질 이미지를 생성하기 위해 인터넷 스케일의 이미지 컬렉션에 대해 학습되었다. Monocular depth estimation의 초석이 실제로 시각적 세계에 대한 포괄적이고 백과사전적인 표현이라면 사전 학습된 diffusion model에서 광범위하게 적용 가능한 depth estimator를 도출하는 것이 가능해야 한다. 본 논문에서는 이 옵션을 탐색하고 depth estimation을 위해 모델을 적용하기 위한 fine-tuning 프로토콜과 함께 Stable Diffusion 기반의 LDM인 Marigold를 개발했다. 사전 학습된 diffusion model의 잠재력을 활용하는 열쇠는 latent space를 그대로 유지하는 것이다. 저자들은 이것이 denoising U-Net만을 수정하고 fine-tuning함으로써 효율적으로 수행될 수 있음을 발견했다. Stable Diffusion을 Marigold로 전환하려면 RGB-D 합성 데이터와 며칠의 GPU 학습만이 필요하다. 이미지의 diffusion prior에 힘입어 Marigold는 탁월한 zero-shot 일반화를 보여주며, 실제 depth map을 보지 않고도 여러 실제 데이터셋에서 SOTA 성능을 달성하였다.

Method

1. Generative Formulation

조건부 diffusion 생성 task로 monocular depth estimation을 제시하고 Marigold를 학습시켜 깊이 $\mathbf{d} \in \mathbb{R}^{W \times H}$에 대한 조건부 분포 $D(\mathbf{d} \; \vert \; \mathbf{x})$를 모델링한다. 여기서 조건 $\mathbf{x} \in \mathbb{R}^{W \times H \times 3}$은 RGB 이미지이다.

조건부 분포의 \(\mathbf{d}_0 := \mathbf{d}\)에서 시작하는 forward process에서는 레벨 \(t \in \{1, \ldots, T\}\)에서 Gaussian noise를 점차적으로 추가하여 다음과 같이 noisy한 샘플 \(\mathbf{d}_t\)를 얻는다.

\[\begin{equation} \mathbf{d}_t = \sqrt{\vphantom{1} \bar{\alpha}_t} \mathbf{d}_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon \\ \textrm{where} \quad \epsilon \sim \mathcal{N} (0,I), \; \bar{\alpha}_t = \prod_{s=1}^t (1 - \beta_s) \end{equation}\]

여기서 \(\{\beta_1, \ldots, \beta_T\}\)는 $T$ step의 프로세스에 대한 variance schedule이다. Reverse process에서는 학습된 파라미터 $\theta$로 parameterize된 조건부 denoising 모델 $\epsilon_\theta (\cdot)$가 \(\mathbf{d}_t\)에서 점차적으로 noise를 제거하여 \(\mathbf{d}_{t-1}\)을 얻는다.

학습 시에는 학습 세트에서 데이터 쌍 $(\mathbf{x}, \mathbf{d})$를 가져와서 $\mathbf{d}$에 임의의 시간 간격 $t$에서 샘플링된 noise $\epsilon$를 더하고 noise 추정치 \(\hat{\epsilon} = \epsilon_\theta (\mathbf{d}_t, \mathbf{x}, t)\)를 계산하고 목적 함수를 최소화하여 파라미터 $\theta$가 업데이트된다. 표준 denoising 목적 함수 $\mathcal{L}$은 DDPM을 따라 다음과 같이 주어진다.

\[\begin{equation} \mathcal{L} = \mathbb{E}_{\mathbf{d}_0, \epsilon \sim \mathcal{N}(0,I), t \sim \mathcal{U}(T)} \| \epsilon - \hat{\epsilon} \|_2^2 \end{equation}\]

Inference 시에는 정규 분포 변수 \(\mathbf{d}_T\)에서 시작하여 학습된 denoiser \(\epsilon_\theta (\mathbf{d}_t, \mathbf{x}, t)\) θ(dt, x, t)를 반복적으로 적용하여 \(\mathbf{d} := \mathbf{d}_0\)가 재구성된다.

데이터에 직접 작동하는 diffusion model 모델과 달리 latent diffusion model(LDM)은 저차원 latent space에서 diffusion step을 수행하여 계산 효율성과 고해상도 이미지 생성에 대한 적합성을 제공한다. Latent space 압축 및 데이터 공간과의 정렬을 가능하게 하기 위해 latent space는 denoiser와 독립적으로 학습된 VAE의 bottleneck에 구성된다. 공식을 latent space로 변환하기 위해 주어진 depth map $\mathbf{d}$에 대해 대응되는 latent code는 인코더 $\mathcal{E}$에 의해 제공된다.

\[\begin{equation} \mathbf{z}^{(\mathbf{d})} = \mathcal{E}(\mathbf{d}) \end{equation}\]

Depth latent code가 주어지면 depth map은 디코더 $\mathcal{D}$를 사용하여 복구될 수 있다.

\[\begin{equation} \hat{\mathbf{d}} = \mathcal{D}(\mathbf{z}^{(\mathbf{d})}) \end{equation}\]

컨디셔닝 이미지 $\mathbf{x}$도 자연스럽게 $\mathbf{z}^{(\mathbf{x})} = \mathcal{E}(\mathbf{x})$로 latent space로 변환된다. 이제 denoiser는 latent space에서 학습된다.

\[\begin{equation} \epsilon_\theta (\mathbf{z}_t^{(\mathbf{d})}, \mathbf{z}^{(\mathbf{x})}, t) \end{equation}\]

Inference 절차에는 디코더 $\mathcal{D}$가 추정된 latent \(\mathbf{z}_0^\mathbf{d}\)에서 데이터 $\hat{\mathbf{d}}$를 재구성하는 단계가 추가된다.

\[\begin{equation} \hat{\mathbf{d}} = \mathcal{D} (\mathbf{z}_0^{(\mathbf{d})}) \end{equation}\]

2. Network Architect

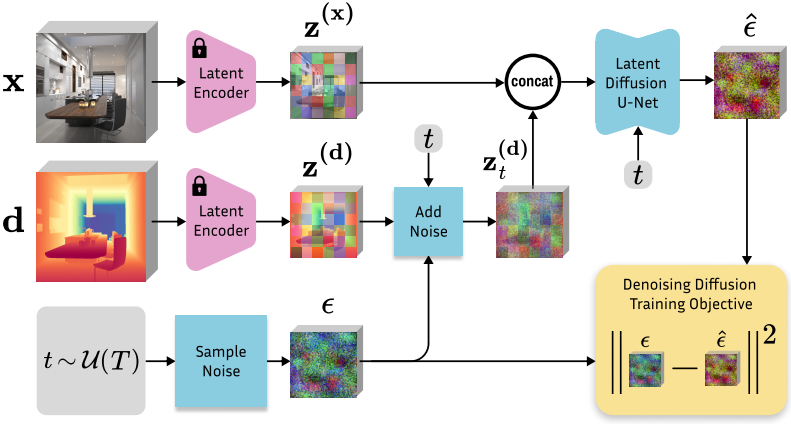
본 논문의 주요 목표 중 하나는 학습 효율성이다. Diffusion model은 종종 학습하는 데 극도로 자원 집약적이기 때문이다. 따라서 LAION-5B에서 매우 좋은 이미지 prior를 학습한 사전 학습된 Stable Diffusion v2를 기반으로 모델을 기반으로 한다. 모델 구성 요소를 최소한으로 변경하여 이를 이미지로 컨디셔닝된 depth estimator로 전환한다. 위 그림에는 fine-tuning 절차의 개요이다.

Depth encoder and decoder

조건부 denoiser를 학습시키기 위해 고정된 VAE를 사용하여 이미지와 해당 depth map을 latent space로 인코딩한다. 3채널(RGB) 입력용으로 설계된 인코더가 1채널 depth map을 수신한다는 점을 고려하여 depth map을 3개 채널로 복제하여 RGB 이미지로 시뮬레이션한다. 이때 깊이 데이터의 데이터 범위는 affine-invariant를 활성화하는 데 중요한 역할을 한다. 저자들은 VAE 또는 latent space 구조를 수정하지 않고도 무시할 수 있는 오차로 사용하여 인코딩된 latent code에서 depth map을 재구성할 수 있음을 확인했다.

\[\begin{equation} \mathbf{d} \approx \mathcal{D}(\mathcal{E}(\mathbf{d})) \end{equation}\]

Inference 시에는 diffusion이 끝난 후 depth latent code를 한 번 디코딩하고 3개 채널의 평균을 depth map 예측으로 사용한다.

Adapted denoising U-Net

Latent denoiser \(\epsilon_\theta (\mathbf{z}_t^{(\mathbf{d})}, \mathbf{z}^{(\mathbf{x})}, t)\)의 컨디셔닝을 구현하기 위해 이미지 latent code와 depth latent code를 feature 차원을 따라 하나의 입력 \(\mathbf{z}_t = \textrm{cat}(\mathbf{z}_t^{(\mathbf{d})}, \mathbf{z}_t^{(\mathbf{x})})\)로 concatenate한다. 그런 다음 latent denoiser의 입력 채널은 확장된 입력 \(\mathbf{z}_t\)를 수용하기 위해 두 배가 된다. 첫 번째 레이어의 activation 크기의 팽창을 방지하고 사전 학습된 구조를 최대한 충실하게 유지하기 위해 입력 레이어의 가중치 텐서를 복제하고 해당 값을 2로 나눈다.

3. Fine-Tuning Protocol

Affine-invariant depth normalization

저자들은 ground-truth depth map $\mathbf{d}$가 VAE의 입력 값 범위와 일치하도록 깊이가 주로 $[-1, 1]$ 범위에 속하도록 선형 정규화를 구현하였다. 이러한 정규화는 두 가지 목적으로 사용된다.

1. 원래의 Stable Diffusion VAE를 사용하는 규칙이다.
2. 데이터 통계와는 독립적으로 표준 affine-invariant depth 표현을 강제한다.

모든 장면은 극단적인 깊이 값을 가진 근거리 및 원거리 평면으로 경계를 설정해야 한다. 정규화는 다음과 같이 계산된 affine 변환을 통해 달성된다.

\[\begin{equation} \tilde{\mathbf{d}} = \bigg( \frac{\mathbf{d} - \mathbf{d}_2}{\mathbf{d}_{98} - \mathbf{d}_2} - 0.5 \bigg) \times 2 \end{equation}\]

여기서 \(\mathbf{d}_2\)와 \(\mathbf{d}_{98}\)은 각 깊이 맵의 2% 및 98% 백분위수에 해당한다. 이 정규화를 통해 Marigold는 순수 affine-invariant depth estimation에 집중할 수 있다.

Training on synthetic data

실제 깊이 데이터셋은 캡처 장비의 물리적 제약과 센서의 물리적 특성으로 인해 깊이 값이 누락되는 문제가 있다. 특히 LiDAR 레이저 빔의 방향을 바꾸는 반사 표면은 잡음과 픽셀 누락의 불가피한 원인이다. 일반화를 달성하기 위해 다양한 실제 데이터셋을 활용한 이전 연구들과 달리 본 논문은 합성 깊이 데이터셋으로만 학습하였다. 깊이 정규화 근거와 마찬가지로 이 결정에는 두 가지 객관적인 이유가 있다.

1. 첫째, 합성 깊이는 본질적으로 dense하고 완전하다. 즉, 모든 픽셀에는 유효한 ground-truth 깊이 값이 있으므로 이러한 데이터를 VAE에 공급할 수 있으며, VAE는 유효하지 않은 픽셀이 있는 데이터를 처리할 수 없다.
2. 합성 깊이는 렌더링 파이프라인에서 보장되는 가장 깨끗한 형태의 깊이이다. 합성 깊이는 가장 깨끗한 예제를 제공하고 짧은 fine-tuning 프로토콜 동안 기울기 업데이트의 잡음을 줄인다.

따라서 남은 우려 사항은 합성 데이터와 실제 데이터 사이의 충분한 다양성 또는 도메인 격차로, 이로 인해 일반화 능력이 제한되는 경우가 있다. 합성 데이터셋을 선택하면 인상적인 zero-shot transfer가 가능해진다.

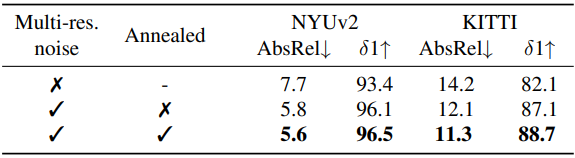
Annealed multi-resolution noise

저자들은 표준 DDPM 공식에 비해 더 빠르게 수렴하고 성능을 크게 향상시키기 위해 multi-resolution noise와 annealed schedule의 조합을 사용하였다. Multi-resolution noise는 서로 다른 스케일의 여러 랜덤 Gaussian noise 이미지를 겹쳐서 구성되며 모두 U-Net 입력 해상도로 업샘플링된다. 제안된 annealed schedule은 $t = T$의 multi-resolution noise와 $t = 0$의 표준 Gaussian noise 사이를 보간한다.

4. Inference

Latent diffusion denoising

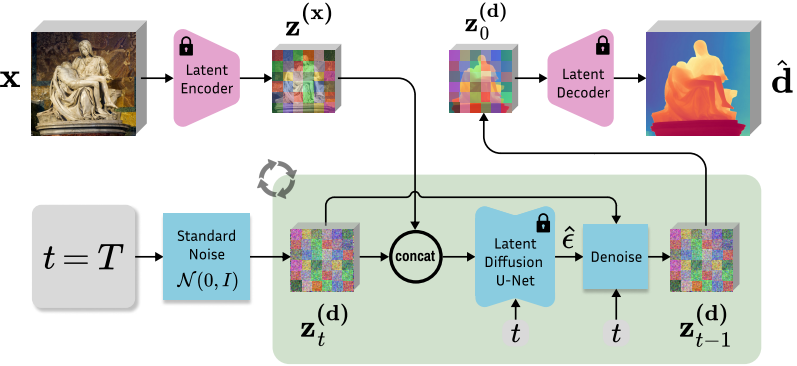
전체 inference 파이프라인은 위 그림과 같다. 입력 이미지를 latent space로 인코딩하고, latent depth를 표준 Gaussian noise로 초기화하고, fine-tuning과 동일한 schedule로 점진적으로 denoising한다. 저자들은 비록 모델이 multi-resolution noise에 대해 학습되었음에도 불구하고 표준 Gaussian noise로 초기화하는 것이 multi-resolution noise를 사용하는 것보다 더 나은 결과를 제공한다는 것을 경험적으로 발견했다. 저자들은 가속화된 inference를 위해 step을 재조정하여 non-Markovian 샘플링을 수행하는 DDIM의 접근 방식을 따른다. 최종 depth map은 VAE 디코더를 사용하여 latent code에서 디코딩되고 채널을 평균 내어 후처리된다.

Test-time ensembling

Inference 파이프라인의 확률론적 특성으로 인해 \(\mathbf{z}_T^{(\mathbf{d})}T\)의 초기 Gaussian noise에 따라 예측이 다양해진다. 본 논문은 이를 활용하여 동일한 입력에 대해 여러 inference pass를 결합할 수 있는 앙상블 방식을 제안하였다. 각 입력 샘플에 대해 inference를 $N$번 실행할 수 있다. 이러한 affine-invariant depth 예측 \(\{\hat{\mathbf{d}}_1, \ldots, \hat{\mathbf{d}}_N\}\)을 집계하려면, 반복적으로 scale \(\hat{s}_i\)와 shift \(\hat{t}_i\)를 공동으로 추정한다.

제안된 목적 함수는 스케일링 및 이동된 예측의 각 쌍 \((\hat{\mathbf{d}^\prime}_i, \hat{\mathbf{d}^\prime}_j)\) 사이의 거리를 최소화한다. 여기서 \(\hat{\mathbf{d}^\prime} = \hat{\mathbf{d}} \times \hat{s} + \hat{t}\)이다. 각 최적화 step에서 픽셀별 중앙값 $\mathbf{m} (x, y) = \textrm{median} (\hat{\mathbf{d}^\prime}_1 (x, y), \ldots, \hat{\mathbf{d}^\prime}_N (x, y))$을 취하여 병합된 depth map $\mathbf{m}$을 계산한다. 추가 정규화 항 $\mathcal{R}$이 추가되어 자명한 해으로의 축소를 방지하고 $\mathbf{m}$의 unit scale을 적용한다. 따라서 목적 함수는 다음과 같다.

\[\begin{equation} \min_{s_1, \ldots, s_N, t_1, \ldots, t_N} \bigg( \sqrt{ \frac{1}{b} \sum_{i=1}^{N-1} \sum_{j=i+1}^N \| \hat{\mathbf{d}^\prime}_i - \hat{\mathbf{d}^\prime}_j \|_2^2 } + \lambda \mathcal{R} \bigg) \\ \textrm{where} \quad \mathcal{R} = \vert \min (m) \vert + \vert 1 − \max(m) \vert, \quad b = \frac{N(N-1)}{2} \end{equation}\]

여기서 $b$는 이미지 쌍의 가능한 조합 수를 나타낸다. 공간 정렬을 위한 반복적인 최적화 후에 병합된 깊이 $\mathbf{m}$은 앙상블 예측으로 사용된다. 이 앙상블 단계에는 독립적인 예측을 정렬하기 위한 ground truth가 필요하지 않다. 이 방식은 $N$에 따라 계산 효율성과 예측 품질 사이의 유연한 trade-off를 가능하게 한다.

Experiments

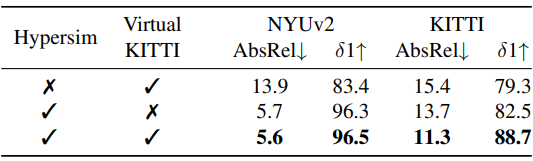
• 학습 데이터셋: Hypersim, Virtual KITTI
• 구현 디테일
  • backbone: Stable Diffusion v2
  • scheduler
    • 학습: DDPM, 1000 steps
    • inference: DDIM, 50 steps
  • 앙상블에서 사용하는 샘플 수: 10
  • iteration: 18,000
  • batch size: 32 (gradient accumulation step: 16)
  • optimizer: Adam (learning rate: $3 times 10^{-5}$)
  • augmentation: random horizontal flipping
  • 학습은 Nvidia RTX 4090 GPU 1개에서 2.5일 소요

1. Evaluation

다음은 SOTA affine-invariant depth estimator와 여러 zero-shot 벤치마크에서 비교한 표이다.

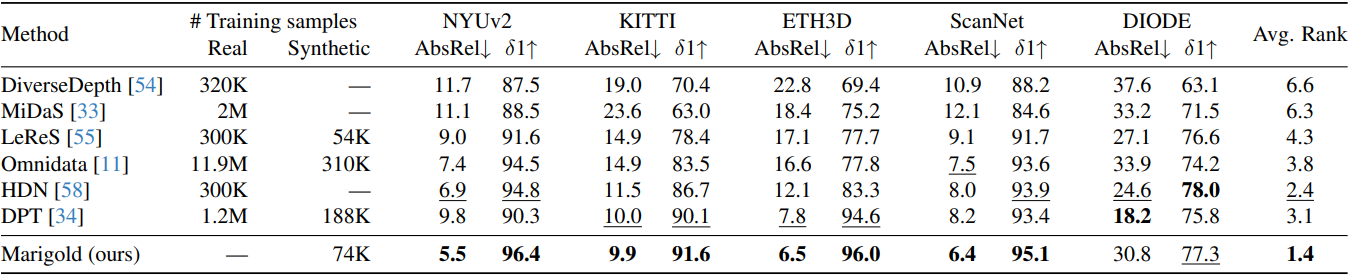
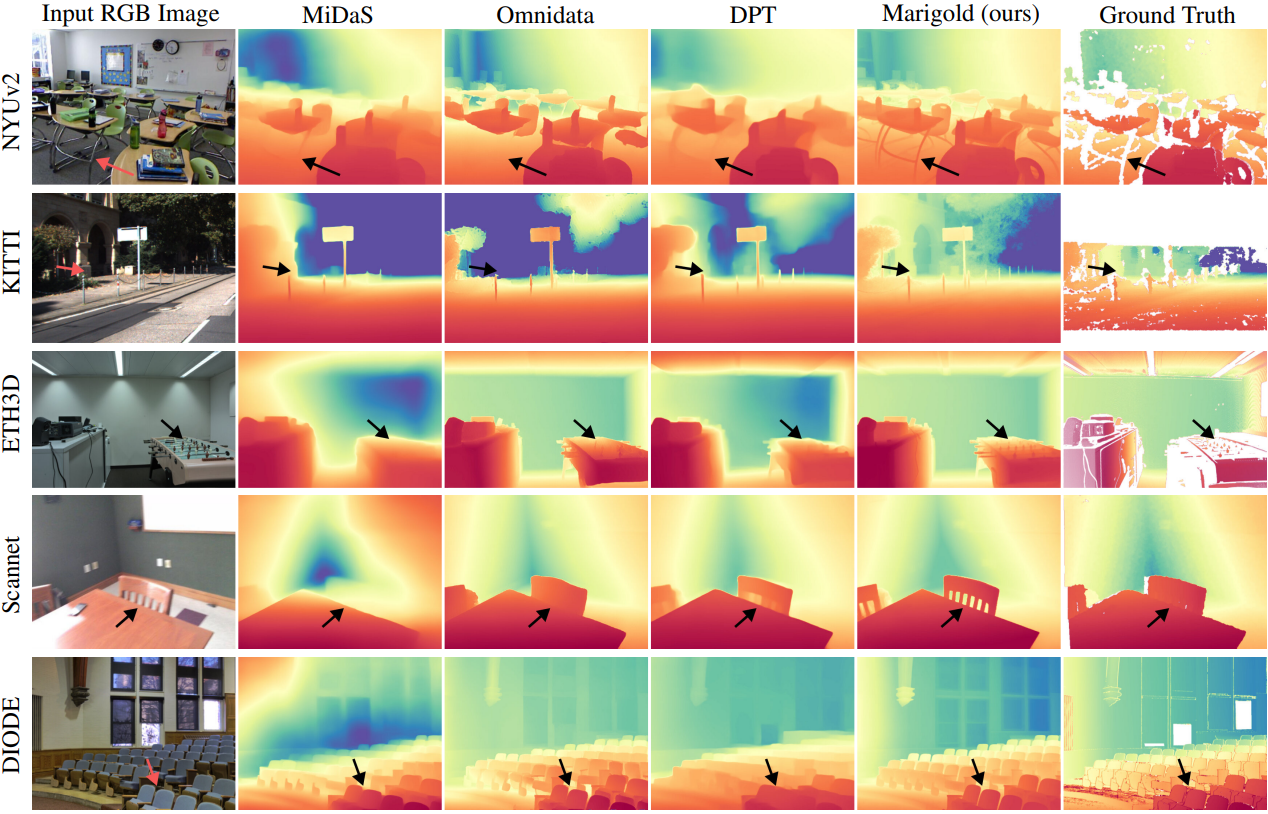
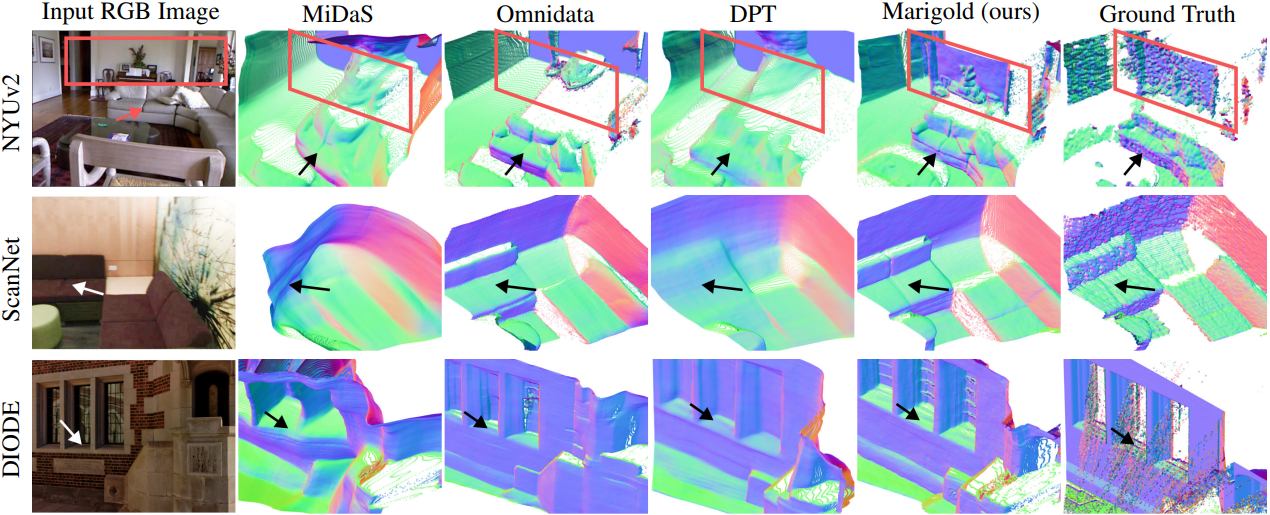
다음은 여러 데이터셋에서 monocular depth estimation 방법들과 비교한 결과이다.

2. Ablation Studies

다음은 학습 noise에 대한 ablation 결과이다.

다음은 학습 데이터셋에 대한 ablation 결과이다.

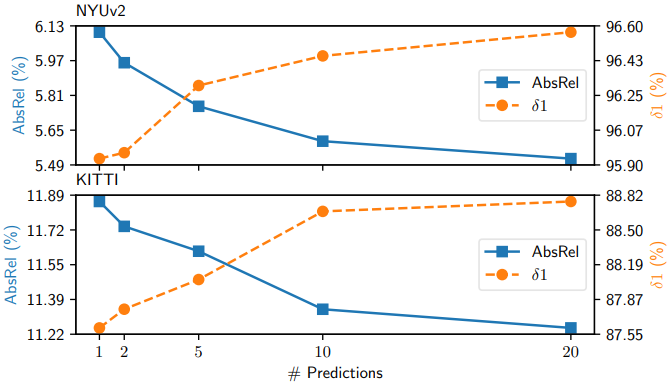
다음은 앙상블 크기에 대한 ablation 결과이다.

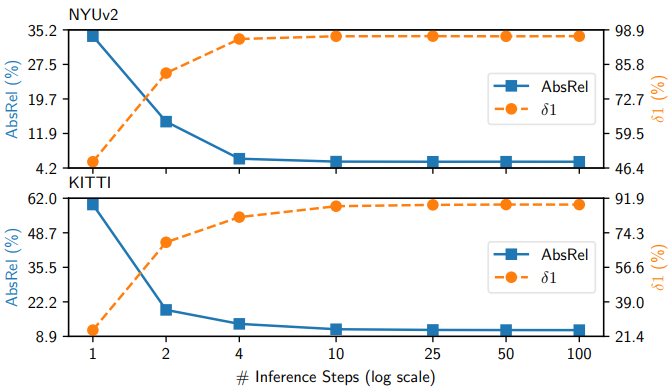
다음은 denoising step에 대한 ablation 결과이다.