[논문리뷰] Autoregressive Image Generation without Vector Quantization

NeurIPS 2024 (Spotlight). [Paper] [Github]
Tianhong Li, Yonglong Tian, He Li, Mingyang Deng, Kaiming He
MIT CSAIL | Google DeepMind | Tsinghua University
17 Jun 2024

Introduction

Autoregressive model은 자연어 처리에서 생성 모델에 대한 사실상의 솔루션이다. Autoregressive model은 이전 단어를 입력으로 사용하여 시퀀스의 다음 단어나 토큰을 예측한다. 언어의 discrete한 특성을 감안할 때 이러한 모델의 입력과 출력은 discrete-valued space에 있다. 이러한 일반적인 접근 방식은 autoregressive model이 본질적으로 discrete한 표현과 연결되어 있다는 널리 퍼진 믿음으로 이어졌다.

결과적으로, autoregressive model을 continuous-valued 도메인, 특히 이미지 생성으로 일반화하는 연구는 데이터를 discrete하게 만드는 데 집중되었다. 일반적으로 채택된 전략은 vector quantization (VQ)로 얻은 유한한 vocabulary를 포함하는 이미지에서 discrete-valued tokenizer를 학습시키는 것이다. 그런 다음 autoregressive model은 언어 모델과 유사하게 discrete-valued token space에서 작동한다.

본 논문에서는 다음 질문을 다루는 것을 목표로 한다.

Autoregressive model을 VQ 표현과 결합하는 것이 필요한가?

저자들은 autoregressive한 특성, 즉 이전 토큰을 기반으로 다음 토큰을 예측하는 것이 ​​값이 discrete하든 continuous하든 무관하다는 점에 주목하였다. 필요한 것은 loss function으로 측정하고 샘플을 추출하는 데 사용할 수 있는 토큰별 확률 분포를 모델링하는 것이다. Discrete-valued 표현들은 범주형 분포로 편리하게 모델링할 수 있지만 개념적으로 필요하지는 않다. 토큰별 확률 분포에 대한 대체 모델이 제시되면 VQ 없이 autoregressive model에 접근할 수 있다.

이러한 관찰을 바탕으로, 저자들은 continuous-valued 도메인에서 작동하는 diffusion process에 의해 토큰별 확률 분포를 모델링하는 것을 제안하였다. 즉, 임의의 확률 분포를 표현하기 위한 diffusion model의 원리를 활용한다.

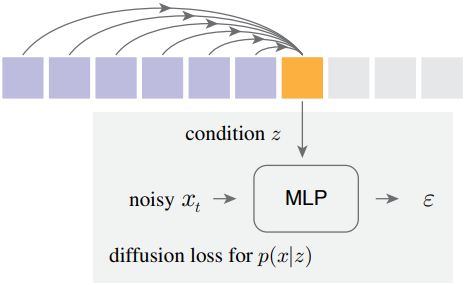
구체적으로, 각 토큰에 대한 벡터 $z$를 autoregressive하게 예측하는데, 이는 denoising network (ex. 작은 MLP)의 조건으로 사용된다. Diffusion process를 통해 출력 $x$에 대한 분포 $p(x \vert z)$를 표현할 수 있다. 이 작은 denoising network는 autoregressive model과 공동으로 학습되며, continuous-valued 토큰을 입력 및 타겟으로 한다. 개념적으로, 각 토큰에 적용된 이 작은 prediction head는 $z$의 품질을 측정하기 위한 loss function처럼 작동한다. 이 loss function을 Diffusion Loss라고 한다.

본 논문의 접근 방식은 discrete-valued tokenizer의 필요성을 제거한다. VQ tokenizer는 학습시키기 어렵고 기울기 근사 전략에 민감하며, 재구성 품질이 continuous-valued tokenizer에 비해 떨어진다. 즉, autoregressive model이 더 높은 품질의 tokenizer의 이점을 누릴 수 있도록 한다.

저자들은 표준 autoregressive model과 masked generative model을 일반화된 autoregressive 프레임워크로 통합하였다. 개념적으로 masked generative model은 알려진 토큰을 기반으로 다음 토큰을 예측하는 autoregressive한 특성을 유지하면서도 무작위 순서로 여러 출력 토큰을 동시에 예측한다. 이를 통해 Diffusion Loss와 함께 원활하게 사용할 수 있는 masked autoregressive (MAR) 모델이 탄생하였다.

Diffusion Loss는 VQ tokenizer의 필요성을 없애고 생성 품질을 개선하며, 다양한 유형의 tokenizer에 유연하게 적용할 수 있다. 또한, 시퀀스 모델의 빠른 속도의 이점을 누린다. Diffusion Loss를 적용한 MAR 모델은 ImageNet 256$\times$256에서 2.0보다 작은 강력한 FID를 달성하면서 하나의 이미지를 0.3초 미만의 속도로 생성할 수 있다. 최고 모델은 1.55 FID를 기록하였다.

Method

본 논문의 이미지 생성 접근법은 토큰화된 latent space에서 작동하는 시퀀스 모델이다. 그러나 VQ tokenizer (ex. VQ-VAE)를 기반으로 하는 이전 방법과 달리, 본 논문은 continuous-valued tokenizer를 사용하는 것을 목표로 한다. 저자들은 시퀀스 모델을 continuous-valued 토큰과 호환되게 만드는 Diffusion Loss를 제안하였다.

1. Rethinking Discrete-Valued Tokens

먼저, autoregressive model에서 discrete-valued 토큰의 역할을 다시 살펴보자. 다음 위치에서 예측할 GT 토큰을 $x$라 하자. Vocabulary 크기가 $K$인 discrete tokenizer를 사용하면 $x$를 0과 $K-1$ 사이의 정수로 표현할 수 있다. Autoregressive model은 continuous한 $D$차원 벡터 $z \in \mathbb{R}^D$를 생성한 다음 $K$-way classifier 행렬 $W \in \mathbb{R}^{K \times D}$로 projection한다. 개념적으로 이 공식은 $p(x \vert z) = \textrm{softmax}(Wz)$ 형태의 범주형 확률 분포를 모델링한다.

생성 모델링의 맥락에서 이 확률 분포는 두 가지 필수적인 속성을 보여야 한다.

1. 추정된 분포와 실제 분포 간의 차이를 측정할 수 있는 loss function
2. Inference 시에 분포 $x \sim p(x \vert z)$에서 샘플을 추출할 수 있는 sampler

범주형 분포의 경우 loss function으로 cross-entropy loss를 사용하며, $p(x \vert z) = \textrm{softmax}(W z / \tau)$로 샘플을 추출한다.

이 분석은 discrete-valued 토큰이 autoregressive model에 필요하지 않다는 것을 시사한다. 대신, 실제로 필요한 것은 분포 모델링을 위한 loss function과 sampler이다.

2. Diffusion Loss

Diffusion model은 임의의 분포를 모델링하는 효과적인 프레임워크를 제공한다. 그러나 모든 픽셀 또는 모든 토큰의 공동 분포를 나타내는 diffusion model의 일반적인 용도와 달리, 본 논문의 경우 diffusion model은 각 토큰의 분포를 나타내는 용도로 사용된다.

다음 위치에서 예측할 GT 토큰을 continuous-valued 벡터 $x \in \mathbb{R}^d$라 하자. Autoregressive model은 이 위치에서 벡터 $z \in \mathbb{R}^D$를 생성한다. 목표는 $p(x \vert z)$를 모델링하는 것이다. Loss function과 sampler는 diffusion model에 따라 정의할 수 있다.

Loss function

확률 분포 $p(x \vert z)$의 loss function은 다음과 같다.

\[\begin{equation} \mathcal{L} (z, x) = \mathbb{E}_{\epsilon, t} [\| \epsilon - \epsilon_\theta (x_t \vert t, z) \|^2] \\ \textrm{where} \; \epsilon \sim \mathcal{N} (0, I), \; x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x + \sqrt{1 - \bar{\alpha}_t} \epsilon \end{equation}\]

Noise 추정기 \(\epsilon_\theta\)는 작은 MLP 네트워크이다. 조건 벡터 $z$가 autoregressive model에서 생성된다는 점에 주목할 가치가 있다. $z = f(\cdot)$의 gradient는 위 식의 loss function에서 전파된다. 개념적으로 위 식은 네트워크 $f(\cdot)$를 학습하기 위한 loss function이다.

Denoising network가 작기 때문에 주어진 $z$에 대해 $t$를 여러 번 샘플링할 수 있다. 이는 $z$를 다시 계산하지 않고도 loss function의 활용도를 개선하는 데 도움이 된다. 저자들은 각 이미지에 대해 학습하는 동안 $t$를 4번 샘플링하였다.

Sampler

Inference 시에는 분포 $p(x \vert z)$에서 샘플을 추출해야 한다. 샘플링은 reverse process를 통해 수행된다.

\[\begin{equation} x_{t-1} = \frac{1}{\sqrt{\alpha_t}} \bigg( x_t - \frac{1 - \alpha_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t \vert t, z) \bigg) + \sigma_t \delta, \quad \delta \sim \mathcal{N} (0,I) \end{equation}\]

$x_T \sim \mathcal{N} (0, I)$로 시작하여 $x_0 \sim p(x \vert z)$를 만족하는 샘플 $x_0$를 생성한다.

범주형 분포를 사용할 때, autoregressive model은 샘플 다양성을 제어하기 위해 temperature $\tau$를 사용할 수 있으며, $\tau$는 autoregressive 생성에서 중요한 역할을 한다.

저자들은 Diffusion Models Beat GANs on Image Synthesis 논문에서 제시된 temperature sampling을 채택하였다. 개념적으로는 score function이 $\frac{1}{\tau} \nabla_x \log p(x \vert z)$인 확률 $p(x \vert z)^{\frac{1}{\tau}}$에서 샘플링하는 방법이다. 실제로는 \(\epsilon_\theta\)를 $\tau$로 나누거나 noise를 $\tau$로 scaling한다. 저자들은 후자의 옵션을 채택하여 sampler에서 $\sigma_t \delta$를 $\tau$로 scaling하였다. 직관적으로 $\tau$는 noise 분산을 조정하여 샘플 다양성을 제어한다.

3. Diffusion Loss for Autoregressive Models

토큰 시퀀스 \(\{x^1, x^2, \ldots, x^n\}\)이 주어지면, autoregressive model은 생성 문제를 next token prediction으로 공식화한다.

\[\begin{equation} p (x^1, \ldots, x^n) = \prod_{i=1}^n p (x^i \, \vert \, x^1, \ldots, x^{i-1}) \end{equation}\]

네트워크는 조건부 확률 \(p (x^i \, \vert \, x^1, \ldots, x^{i-1})\)을 나타내는 데 사용되며, $x^i$는 continuous-valued일 수 있다. 이 식을 두 부분으로 다시 쓸 수 있다. 먼저 이전 토큰에서 작동하는 네트워크 (ex. Transformer)로 조건 벡터 \(z^i = f(x^1, \ldots, x^{i-1})\)를 생성한다. 그런 다음 $p(x^i \vert z^i)$로 다음 토큰의 확률을 모델링한다. Diffusion Loss를 $p(x^i \vert z^i)$에 적용할 수 있다. Gradient는 $f(\cdot)$의 파라미터를 업데이트하기 위해 $z^i$로 역전파된다.

4. Unifying Autoregressive and Masked Generative Models

MaskGIT, MAGE와 같은 masked generative model은 autoregressive, 즉 다음 토큰 예측의 광범위한 개념으로 일반화될 수 있다.

Bidirectional attention은 autoregression을 수행할 수 있다.

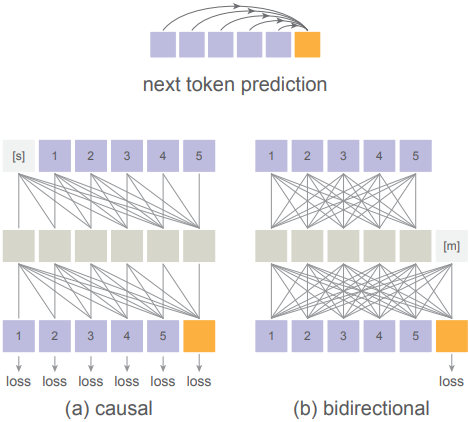
Transformers를 사용할 때 autoregressive model은 causal attention에 의해 널리 구현되지만, bidirectional attention에 의해서도 수행될 수 있다. Autoregressive의 목표는 이전 토큰을 고려하여 다음 토큰을 예측하는 것이다. 이전 토큰이 다음 토큰과 통신하는 방식을 제한하지 않는다.

Masked Autoencoder (MAE)에서 한 것처럼 bidirectional attention을 채택할 수 있다. 구체적으로, 먼저 알려진 토큰에 MAE 스타일 인코더를 적용한다. 그런 다음 인코딩된 시퀀스를 마스크 토큰들과 concat하고 이 시퀀스를 MAE 스타일 디코더에 매핑한다. 마스크 토큰의 위치 임베딩을 통해 디코더는 어떤 위치를 예측해야 하는지 알 수 있다. Causal attention과 달리 여기서 loss는 알려지지 않은 토큰에서만 계산된다.

MAE 스타일에서는 알려진 모든 토큰이 서로를 볼 수 있도록 허용하고, 알려지지 않은 모든 토큰이 알려진 모든 토큰을 볼 수 있도록 허용한다. 이 full attention은 causal attention보다 토큰 간에 더 나은 통신을 도입한다. Inference 시에는 이 bidirectional attention을 사용하여 단계당 하나 이상의 토큰을 생성할 수 있으며, 이는 일종의 autoregressive이다. 그 대신, causal attention의 key-value (kv) cache를 사용하여 inference 속도를 높일 수 없다. 하지만 여러 토큰을 함께 생성할 수 있으므로 생성 단계를 줄여 inference 속도를 높일 수 있다. 토큰 간에 full attention은 품질을 크게 개선하고 더 나은 속도/정확도 trade-off를 제공한다.

무작위 순서의 autoregressive model

Masked generative model에 연결하기 위해 무작위 순서의 autoregressive model을 고려한다. 모델은 무작위로 섞인 시퀀스를 받게 된다. 이 무작위 순서는 각 샘플마다 다르다. 이 경우, 예측할 다음 토큰의 위치는 모델에서 접근 가능해야 한다. MAE와 유사한 전략을 채택하여, 디코더 레이어에 위치 임베딩을 추가한다. 이 위치 임베딩은 섞이지 않은 위치에 해당하며, 예측할 위치를 알려준다. 이 전략은 causal attention과 bidirectional attention 모두에 적용 가능하다.

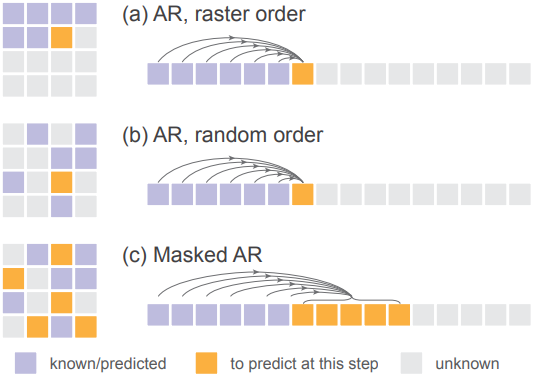
위 그림에 표시된 대로, 무작위 순서의 autoregressive model는 한 번에 하나의 토큰이 생성되는 특별한 형태의 masked generation처럼 작동한다.

Masked autoregressive models

Masked generative model은 알려진/예측된 토큰을 기반으로 토큰의 랜덤한 부분집합을 예측한다. 이는 토큰 시퀀스를 무작위 순서로 섞은 다음 이전 토큰을 기반으로 여러 토큰을 예측하는 것으로 공식화할 수 있다. 개념적으로 이는 autoregressive하며 조건부 분포를 추정하는 것으로 쓸 수 있다.

\[\begin{equation} p(\{x^i, x^{i+1}, \ldots, x^j\} \, \vert \, x^1, \ldots, x^{i-1}) \end{equation}\]

이 autoregressive model을 다음과 같이 쓸 수 있다.

\[\begin{equation} p(x^1, \ldots, x^n) = p(X^1, \ldots, X^K) = \prod_{k=1}^K p (X^k \, \vert \, X^1, \ldots, X^{k-1}) \\ \textrm{where} \; X^k = \{x^i, x^{i+1}, \ldots, x^j\} \end{equation}\]

여기서 $X^k$는 $k$번째 단계에서 예측할 토큰 세트이다. 이는 본질적으로 “next set-of-tokens prediction”이며 따라서 autoregressive의 일반적인 형태이기도 하다. 이 변형을 Masked Autoregressive (MAR) 모델이라고 한다. MAR은 여러 토큰을 동시에 예측할 수 있는 무작위 순서 autoregressive model이다.

MAR은 각 토큰의 확률 분포에 적용된 temperature $\tau$로 토큰을 샘플링한다. 반면 MAGE는 예측할 토큰의 위치를 ​​샘플링하기 위해 temperature를 적용한다. 이는 완전히 무작위한 순서가 아니므로 학습과 inference 사이에 차이가 생긴다.

Experiments

• 데이터셋: ImageNet 256$\times$256

1. Properties of Diffusion Loss

다음은 diffusion loss와 cross-entropy loss를 비교한 표이다.

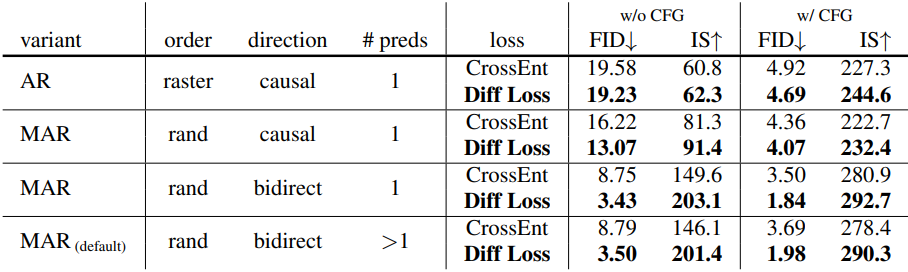
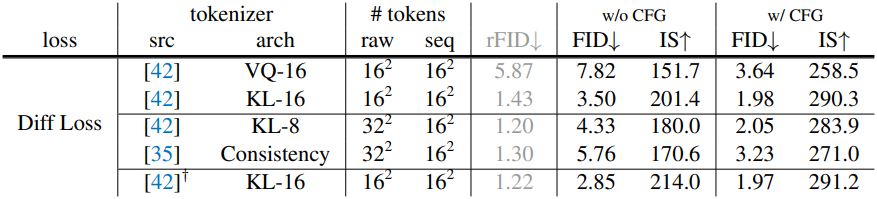
다음은 여러 tokenizer에서의 성능을 비교한 표이다.

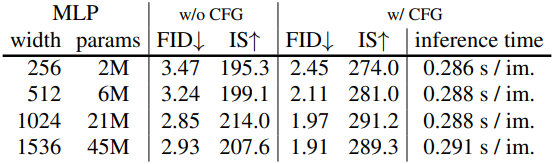
다음은 denoising MLP의 크기에 따른 성능을 비교한 표이다. Inference time은 전체 생성 모델을 포함한 시간이다.

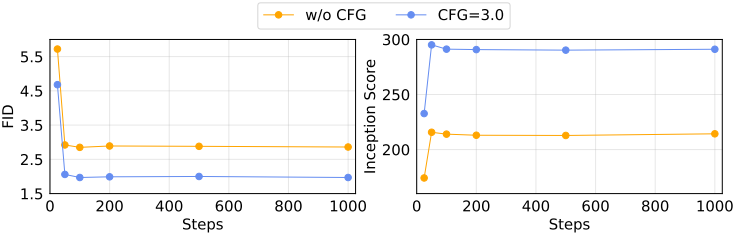
다음은 sampling step 수에 따른 성능을 비교한 그래프이다.

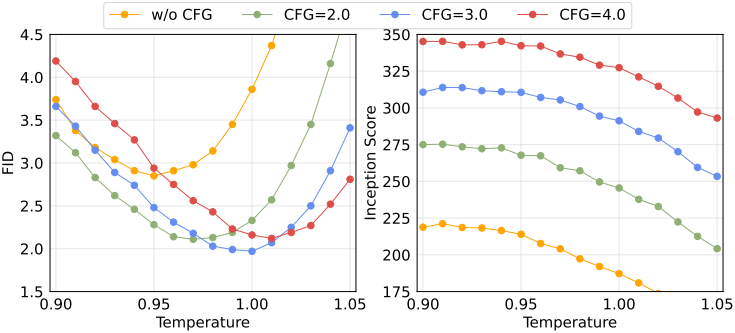
다음은 temperature $\tau$에 따른 성능을 비교한 그래프이다.

2. Properties of Generalized Autoregressive Models

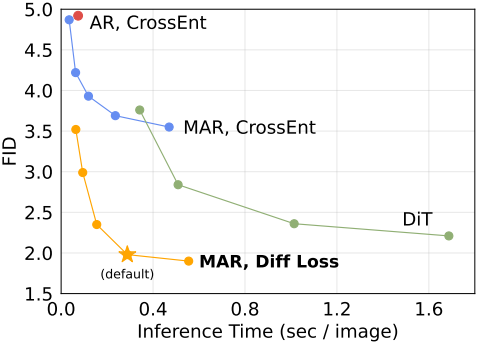
다음은 속도와 정확도 사이의 trade-off를 다른 방법들과 비교한 그래프이다.

3. Benchmarking with Previous Systems

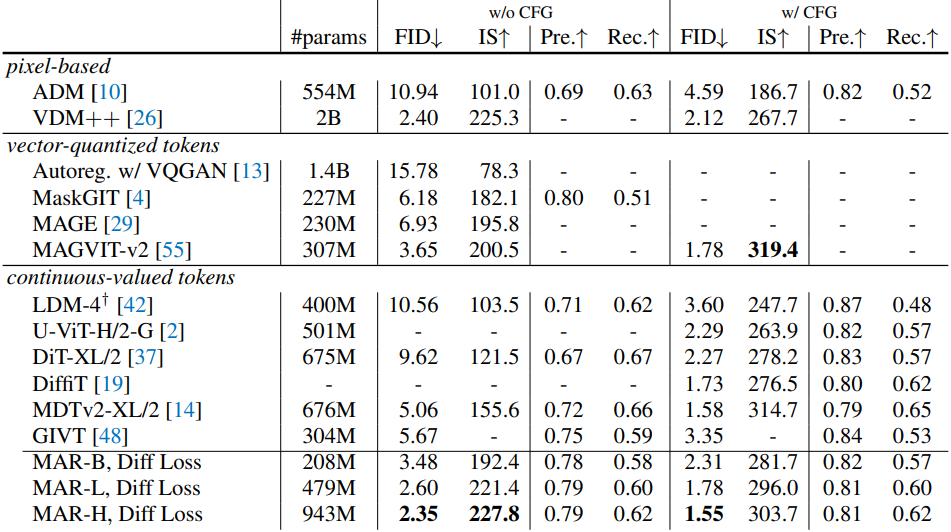
다음은 다른 방법들과 성능을 비교한 표이다.

다음은 Diffusion Loss를 사용한 MAR-H의 생성 예시들이다.