[논문리뷰] Mani-GS: Gaussian Splatting Manipulation with Triangular Mesh

CVPR 2025. [Paper] [Page] [Github]
Xiangjun Gao, Xiaoyu Li, Yiyu Zhuang, Qi Zhang, Wenbo Hu, Chaopeng Zhang, Yao Yao, Ying Shan, Long Quan
The Hong Kong University of Science and Technology | Tencent | Nanjing University
28 May 2024

Introduction

최근 3DGS는 높은 충실도와 빠른 렌더링 성능으로 인해 미분 가능한 렌더링 분야에서 큰 주목을 받고 있다. 그러나 명시적인 3D 표현임에도 불구하고, 고품질 렌더링을 유지하면서 3DGS를 효과적으로 조작할 수 있는 방법이 부족하다.

본 논문은 3DGS 조작을 가능하게 하고 고품질의 사실적인 렌더링을 달성하는 방법을 제안하였다. 핵심 통찰력은 삼각형 메쉬를 프록시로 사용하여 3DGS를 조작하는 것이며, 이를 통해 3DGS 자체 적응을 통해 메쉬 조작을 3DGS로 직접 전송할 수 있다. 본 논문의 방법을 사용하면 고품질의 결과로 큰 변형, 로컬한 조작, soft body simulation이 가능하며, 다양한 유형의 조작에 대한 다양한 알고리즘을 설계할 필요도 없다.

메쉬를 통해 제어 가능한 3DGS 조작을 달성하기 위한 직관적인 접근 방식은 GS를 삼각형에 완벽하게 배치하고 GS를 충분히 얇게 만드는 것이다. 메쉬 조작 후 GS는 SuGaR에서 사용된 것처럼 부착된 삼각형에 따라 rotation 및 위치를 자동으로 조정한다. 그러나 SuGaR는 메쉬 형상의 정확성에 크게 의존하며 메쉬 렌더링의 결함을 물려받는다. 특히 부정확한 부분의 경우 SuGaR는 렌더링 중에 누락된 부분을 다시 칠하거나 중복된 부분을 제거할 수 없다.

재구성 과정에서 연결된 Gaussian의 위치에 offset을 추가하는 것은 메쉬 부정확성을 보상하는 좋은 해결책처럼 보일 수 있다. 그러나 이 고정 offset은 조작 후 변형된 공간에 잘 일반화될 수 없다. 본 논문에서는 각 삼각형에 대한 로컬 좌표계를 정의하는 것을 제안하였다. 이를 local triangle space라고 한다. 그런 다음 각 삼각형에 Gaussian을 바인딩하고, 연결된 local triangle space에서 rotation, 위치, scaling을 포함한 Gaussian 속성을 최적화한다.

메쉬 조작 시, local triangle space의 속성은 변경되지 않지만, 글로벌한 Gaussian 위치, scaling 및 rotation은 제안된 공식에 따라 자체 적응적으로 조정된다. 결과적으로, 렌더링 품질을 유지하면서 삼각형 메쉬를 사용하여 3DGS를 조작할 수 있다. Gaussian이 삼각형 외부에서 자유롭게 설정되므로, Gaussian이 부정확한 메쉬에 바인딩된 경우에도 고충실도 조작을 지원할 수 있으며, 메쉬 정확도가 다소 낮아도 잘 작동한다.

Method

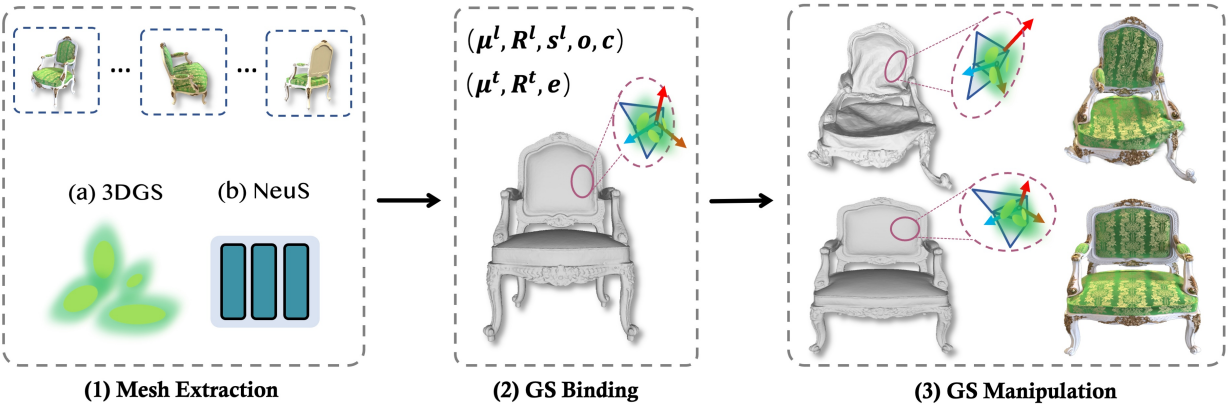
1. Mesh Extraction

저자들은 다양한 메쉬 추출 및 재구성 기법을 사용하였다.

Marching Cube: 인접한 Gaussian들의 alpha 값을 marching cube 샘플링 포인트들의 밀도 값으로 요약한다. 이 방법을 사용하여 추출된 메쉬는 얇고 작은 구조를 종종 무시한다.
Screened Poisson Reconstruction: 3DGS를 포인트 클라우드의 한 유형으로 보고, Poisson reconstruction 알고리즘을 사용하여 메쉬를 추출한다. 3D Gaussian은 재구성을 위한 normal 벡터를 갖지 않기 때문에, 3D Gaussian에 대해 추가적인 normal 속성 $\textbf{n}$을 할당하고, depth map에서 도출된 normal로 학습시킨다. Nomral 속성을 사용하여 3DGS를 학습한 후, Screened poisson reconstruction 재구성 알고리즘을 사용하여 메쉬를 추출할 수 있다.
Neural Implicit Surfaces: NeuS를 활용하여 암묵적 표현으로부터 고품질 표면을 추출한다. NeuS 메쉬는 삼각형 수가 많아 학습 속도와 inference 속도 모두에 부정적인 영향을 미친다. 메쉬 decimation 기법을 사용하여 삼각형 수를 약 30만 개로 줄인다.

2. Binding Gaussian Splatting on Mesh

3DGS는 명시적인 3D 표현임에도 불구하고, 고품질 렌더링을 유지하면서 3DGS를 효과적으로 조작할 수 있는 방법이 현재로서는 부족하다. 본 논문의 주요 목표는 3DGS를 메쉬 삼각형과 연결하여 메쉬 편집 후 3DGS 및 렌더링 결과를 조작할 수 있도록 하는 것이다.

$K$개의 vertex $\{\textbf{v}_i\}_{i=1}^K$와 $M$개의 삼각형 $\{\textbf{f}_i\}_{i=1}^M$을 갖는 삼각형 메쉬 $\textbf{T}$가 주어졌을 때, 본 논문의 목표는 메쉬 삼각형에 바인딩된 3DGS 모델을 구성하고 각 Gaussian 속성 $\{\boldsymbol{\mu}_i, \textbf{q}_i, \textbf{s}_i, o_i, \textbf{c}_i\}$를 최적화하는 것이다.

주어진 메쉬 $\textbf{T}$의 세 vertex $(\textbf{v}_1, \textbf{v}_2, \textbf{v}_3)$으로 구성된 각 삼각형 $\textbf{f}$에 대해, 이 삼각형에 3개의 Gaussian을 초기화한다. 구체적으로, 초기화된 Gaussian의 평균 위치 $\boldsymbol{\mu}$는 다음과 같다.

\[\begin{equation} \boldsymbol{\mu} = (w_1 \textbf{v}_1 + w_2 \textbf{v}_2 + w_3 \textbf{v}_3) \end{equation}\]

($\textbf{w} = (w_1, w_2, w_3)$은 삼각형에 부착된 각 Gaussian의 미리 정의된 중심 좌표, $w_1 + w_2 + w_3 = 1$)

메쉬 위의 Gaussian

직관적인 방법은 SuGaR와 같이 삼각형에 3DGS를 완벽하게 연결하는 것이다. Rotation 행렬을 $\textbf{R} = \{\textbf{r}_1, \textbf{r}_2, \textbf{r}_3\}$, scaling 벡터를 $\textbf{s} = (s_1, s_2, s_3)$이라 하면, SuGaR는 $s_1 = \epsilon \approx 0$으로 설정하여 메쉬에서 평평한 Gaussian 분포를 갖는 3DGS를 학습시킨다. $\textbf{r}_1$은 연결된 삼각형의 normal 벡터 $\textbf{n}$으로 정의된다. Gaussian은 학습 가능한 scaling factor가 2개뿐이며, quaternion이 아닌 학습 가능한 2D rotation이 1개뿐이어서 Gaussian을 평평하게 유지하고 메쉬 삼각형과 정렬한다.

이 바인딩 전략은 메쉬 정확도에 크게 의존하므로 복잡한 물체 렌더링을 모델링할 때 3DGS의 유연성이 제한된다. 메쉬 정확도가 낮으면 형상이 누락되거나 중복된 부분을 보상할 수 없다. 반대로, 메쉬 정확도가 높더라도 실제 값과 차이가 있는 경우, 부정확한 메쉬와 멀티뷰 이미지 간의 시점 불일치로 인해 흐릿한 효과가 발생하는 경향이 있다. 전반적으로 이러한 바인딩 전략은 메쉬 렌더링의 단점을 그대로 이어받는다.

오프셋이 있는 메쉬 위의 Gaussian

추출된 메쉬의 부정확성을 보완하기 위해 Gaussian 3D 평균 $\boldsymbol{\mu}$에 offset $\Delta \boldsymbol{\mu}$를 추가하는 것이 더 좋을 것이다. 이렇게 하면 Gaussian이 부착된 삼각형 $\textbf{f}$에서 벗어날 수 있다. 재구성된 정적 물체의 렌더링 품질은 향상될 수 있지만, 이 offset 필드는 일반화되지 않는다. 3DGS 간의 상대적 위치가 일치하지 않아 조작된 물체에 노이즈가 많고 예상치 못한 렌더링 왜곡이 발생할 수 있다.

Triangle Shape Aware Gaussian Binding and Adaption

조작 후 고충실도 렌더링 결과를 유지하기 위해서는, 3D 평균과 rotation 모두에서 local rigidity를 유지하고 Gaussian 행렬 간의 상대적 위치를 유지하는 것이 핵심이다. 핵심은 각 triangle space에서 로컬 좌표계를 정의하는 것이다.

Triangle space의 첫 번째 축 방향은 첫 번째 edge의 방향으로 정의되며, 두 번째 축 방향은 삼각형의 normal 방향으로 정의된다. 세 번째 축 방향은 첫 번째 축과 두 번째 축의 외적으로 정의된다. 그러면 삼각형 좌표계의 rotation은 다음과 같다.

\[\begin{equation} \textbf{R}^t = [\textbf{r}_1^t, \textbf{r}_2^t, \textbf{r}_3^t] = [\frac{\textbf{v}_2 - \textbf{v}_1}{\| \textbf{v}_2 - \textbf{v}_1 \|}, \textbf{n}^t, \frac{\textbf{v}_2 - \textbf{v}_1}{\| \textbf{v}_2 - \textbf{v}_1 \|} \times \textbf{n}^t] \\ \textrm{where} \; \textbf{n}^t = \frac{(\textbf{v}_2 - \textbf{v}_1) \times (\textbf{v}_3 - \textbf{v}_1)}{\| (\textbf{v}_2 - \textbf{v}_1) \times (\textbf{v}_3 - \textbf{v}_1) \|} \end{equation}\]

($\textbf{v}_1$, $\textbf{v}_2$는 각각 첫 번째와 두 번째 vertex 위치)

그런 다음, 원래 3DGS의 글로벌 위치와 rotation 대신 triangle space에서 Gaussian의 로컬 위치 $\boldsymbol{\mu}^l$과 로컬 회전 $\textbf{R}^l$을 최적화한다. 그러면 3DGS의 글로벌 rotation, scale, 위치는 다음과 같다.

\[\begin{equation} \textbf{R} = \textbf{R}^t \textbf{R}^l, \quad \textbf{s} = \textbf{s}^l, \quad \boldsymbol{\mu} = \textbf{R}^t \boldsymbol{\mu}^l + \boldsymbol{\mu}^t \end{equation}\]

($\boldsymbol{\mu}^t$는 각 삼각형 중심의 글로벌 좌표)

실제로는 $N$개의 로컬 Gaussian을 초기화하고, 초기화된 위치가 삼각형 상에 균일하게 위치하는 각 Gaussian에 대해 바인딩한다.

이러한 바인딩 전략을 통해 3DGS는 메쉬 조작 후 Gaussian의 상대적 위치와 rotation을 유지하면서 삼각형 밖으로 이동할 수 있다. 그러나 메쉬 조작 후에는 삼각형 중심뿐만 아니라 삼각형 모양도 변경된다. 변경된 삼각형 모양에 따라 로컬 Gaussian 위치와 scaling도 그에 따라 조정되어야 한다.

\[\begin{equation} \textbf{R} = \textbf{R}^t \textbf{R}^l, \quad \textbf{s} = \beta \textbf{e} \textbf{s}^l, \quad \boldsymbol{\mu} = \textbf{e} \textbf{R}^t \boldsymbol{\mu}^l + \boldsymbol{\mu}^t \end{equation}\]

($\beta$는 hyperparameter, $\textbf{e} = [e_1, e_2, e_3]$는 adaption vector)

첫 번째 축은 첫 번째 edge를 따라가므로, $e_1$은 삼각형 첫 번째 edge의 길이 $l_1$으로 설정한다. 두 번째 축은 normal 방향을 따라가므로, $e_2 = 0.5 (e1 + e3)$로 설정한다. 세 번째 축은 첫 번째 edge에 수직이므로, $e_3$는 두 번째와 세 번째 모서리의 평균 길이인 $0.5 (l_2 + l_3)$로 설정한다.

3. Manipulate Gaussian Splatting through Mesh

모델 학습 및 메쉬 조작이 완료되면, 앞서 설명한 방법으로 3DGS를 즉시 조작하고 적응시킨다. 메쉬 조작 중에 local triangle space의 속성은 변경되지 않는다. 삼각형 rotation, 위치, edge 길이는 즉시 계산될 수 있다. 따라서 글로벌 Gaussian 위치, scaling, rotation을 적응적으로 조정할 수 있다.

Experiments

구현 디테일
- 3만 iteration 동안 3DGS 학습 후 메쉬 추출
- 추출된 메쉬로 초기화한 Gaussian을 2만 iteration 동안 학습
- GPU: NVIDIA A100 1개

1. Evaluation

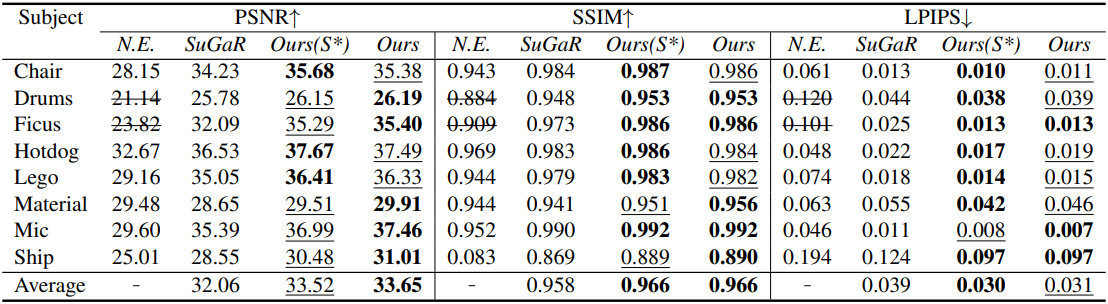
다음은 NeRF Synthetic 데이터셋에 대한 비교 결과이다.

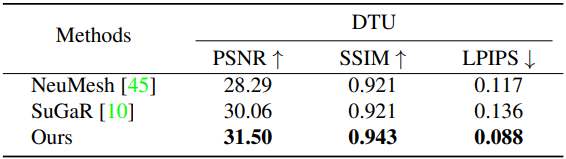
다음은 DTU 데이터셋에 대한 비교 결과이다.

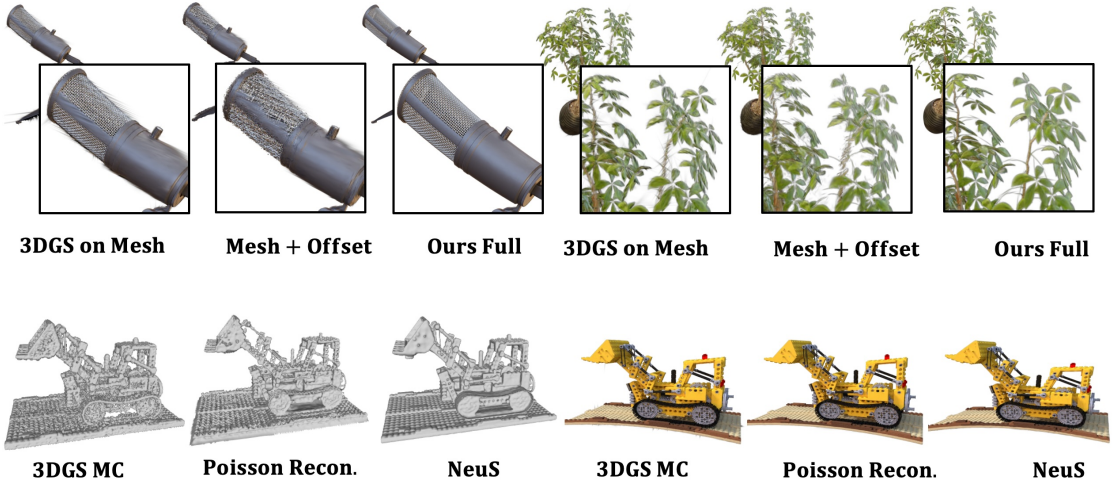
다음은 부정확한 메쉬에 대한 바인딩 결과를 비교한 것이다.

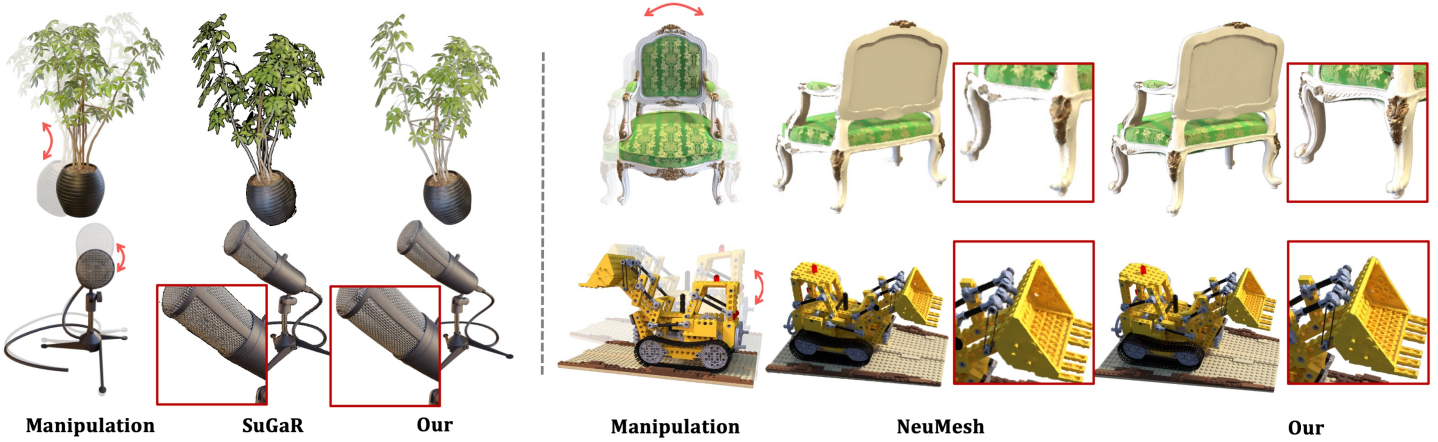
다음은 조작 후의 렌더링 결과를 비교한 것이다.

다음은 (위) 로컬한 조작과 (아래) soft body simulation의 예시들이다.

2. Ablation Study

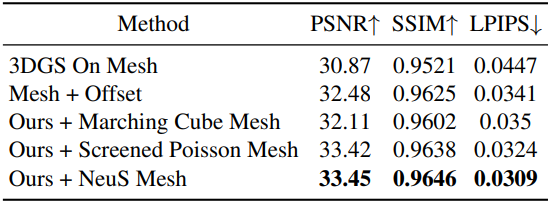
다음은 바인딩 전략과 메쉬 추출 방법에 대한 ablation 결과이다.

JiYeop Kim