[논문리뷰] Make-A-Shape: a Ten-Million-scale 3D Shape Model
ICML 2024. [Paper] [Page] [Github]
Ka-Hei Hui, Aditya Sanghi, Arianna Rampini, Kamal Rahimi Malekshan, Zhengzhe Liu, Hooman Shayani, Chi-Wing Fu
The Chinese University of Hong Kong | Autodesk AI Lab
12 Nov 2024

Introduction
3D 생성 모델을 학습하면 고유한 과제가 발생한다.
- 3D의 추가 차원은 변수의 수를 늘려 학습에 더 많은 파라미터와 메모리를 요구한다. 특히, U-Net 기반 diffusion model은 GPU의 처리 능력을 초과하는 메모리 집약적 feature map을 생성하므로 학습 시간이 크게 늘어난다.
- 3D 데이터는 상당한 입출력 부담을 준다. 대규모 모델 학습은 데이터 저장을 위해 클라우드 서비스에 의존하므로 3D 데이터를 처리하면 저장 비용이 크게 증가하고 각 학습 iteration에 대한 데이터 다운로드 시간이 길어진다.
- 3D shape은 2D 이미지와 달리 불규칙하고 sparse하다. 대규모 학습을 위해 3D shape을 효율적으로 표현하는 방법은 여전히 미해결 문제이다.
본 논문은 1천만 개의 3D shape들로 학습된 대규모 모델을 생성할 수 있도록 효율적인 학습과 압축된 3D 표현을 목표로 하였다. 먼저, 3D shape을 압축적으로 인코딩하면서도 coarse 계수와 detail 계수를 모두 고려할 수 있는 새로운 3D 표현인 wavelet-tree 표현을 설계했다. 저자들은 고주파 디테일을 효과적이고 효율적으로 캡처할 수 있는 대규모 모델 학습을 가능하게 하는 여러 기법을 설계했다.
- Subband 계수 필터링: 정보가 풍부한 계수를 선택적으로 유지하여, shape을 압축적이면서도 포괄적으로 표현할 수 있게 한다.
- Subband 계수 패킹: 이러한 계수를 diffusion model에서 사용하기 적합한 압축된 그리드 형식으로 재구성한다.
- Subband 적응형 학습 전략: 학습 과정에서 coarse 계수와 detail 계수 간의 균형을 효과적으로 유지한다.
또한 저자들은 포인트 클라우드, voxel, 이미지와 같은 다양한 입력 모달리티를 수용할 수 있는 다양한 컨디셔닝 메커니즘을 개발했다. 따라서, 새로운 표현 방식은 압축적이면서도 대부분의 shape 정보를 충실하게 유지할 수 있으며, 동시에 대규모 생성 모델의 효과적인 학습을 가능하게 한다. 이 방법을 Make-A-Shape이라고 부른다.
Make-A-Shape는 이전 연구들에 비해 몇 가지 명확한 장점을 가지고 있다.
- Wavelet-tree 표현은 매우 표현력이 뛰어나 최소한의 손실로 shape을 인코딩할 수 있다. 예를 들어, $256^3$ 그리드는 1초 안에 인코딩될 수 있으며, IoU는 99.56%이다.
- Wavelet-tree 표현은 압축적이며 입력 변수의 수가 적고, 추가 오토인코더 학습이 필요하지 않으며, 더 높은 품질을 갖는다.
- 빠른 스트리밍과 학습이 가능하다.
- 단일/다중 뷰 이미지, 포인트 클라우드, 저해상도 voxel과 같은 다양한 모달리티로 컨디셔닝할 수 있어 다양한 다운스트림 애플리케이션을 구현할 수 있다.
- 빠른 생성을 지원하여 고품질 shape을 생성하는 데 불과 몇 초가 걸린다.
Method
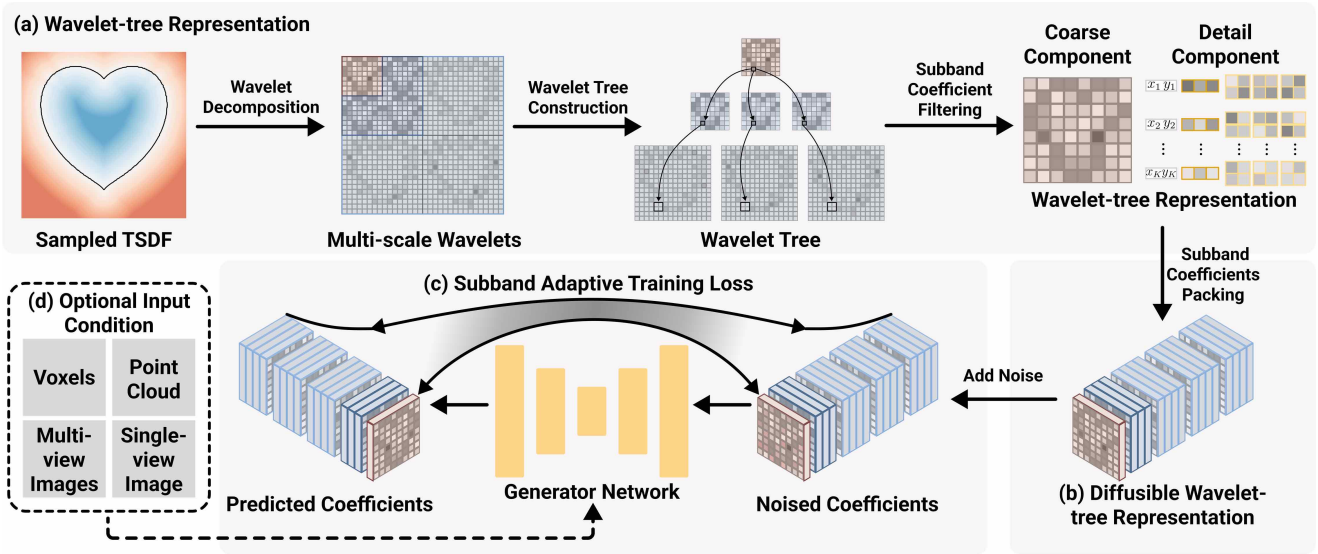
1. Wavelet-tree representation
저자들은 wavelet-tree 표현이라고 불리는 새롭고 효율적이며 표현력이 뛰어난 3D 표현을 공식화하였다. 먼저 3D shape을 해상도 $256^3$의 TSDF로 변환한 다음 웨이블릿 변환을 사용하여 TSDF를 coarse 계수 $C_0 \in \mathbb{R}^{46^3}$과 detail 계수 $D_0 \in \mathbb{R}^{(2^d - 1) \times 46^3}$, $D_1 \in \mathbb{R}^{(2^d - 1) \times 76^3}$, $D_2 \in \mathbb{R}^{(2^d - 1) \times 136^3}$으로 분해한다. 여기서 $d$는 차원을 나타낸다. 3차원에서 각 $D_i$는 $2^3 − 1 = 7$개의 볼륨의 집합이며, 이를 subband volume이라고 한다.
위 그림은 2차원으로 설명한 것이다. 여기서 $d = 2$이고 각 $D_i$는 $2^2 − 1 = 3$개의 subband volume을 갖는다. Coarse 계수 $C_0$는 저주파 성분을 인코딩하고 전체 3D 토폴로지를 나타내는 반면, detail 계수는 고주파 정보를 포함한다. 중요한 점은 이 표현이 손실 없어 역 웨이블릿 변환을 통해 TSDF로의 전단사 변환이 가능하다는 것이다.
웨이블릿 계수 트리
웨이블릿 계수 간의 관계를 활용한다. $C_0$(부모)의 각 coarse 계수는 $D_0$(자식)의 연관된 detail 계수에 계층적으로 연결된다. 이 부모-자식 관계는 후속 레벨 (ex. $D_0$에서 $D_1$로)을 반복하여 $C_0$의 계수를 루트로 하고 동일한 부모를 공유하는 계수를 형제로 하는 웨이블릿 계수 트리를 만든다.
손실이 없음에도 불구하고, 웨이블릿 계수는 $D_1$, $D_2$와 같은 여러 개의 고해상도 계수 볼륨을 포함하는데, 이는 컴팩트하지 않고 데이터 로딩과 모델 학습 모두에서 비효율적일 수 있어 대규모 학습에 대한 확장성이 떨어진다.
저자들은 표현을 더 컴팩트하게 만들고 입출력 및 학습 부담을 덜어주기 위해, 웨이블릿 계수에 대한 여러 경험적 연구를 수행했고 네 가지 주요 관찰 결과를 확인했다.
- Shape 재구성을 위한 각 계수의 유의도는 크기와 양의 상관 관계가 있다. 계수의 크기가 threshold 아래로 떨어지면 자식은 크기가 작아 shape에 최소한으로 기여할 가능성이 높다. (1,000개의 무작위 shape의 $D_0$ subband에서 계수의 96.1% 이상이 이 가설을 충족)
- 형제 계수의 크기는 양의 상관 관계가 있다. (1,000개의 무작위 shape에서 0.35의 양의 상관 관계)
- $C_0$에는 형제보다 더 많은 shape 정보가 포함되어 있다. $C_0$의 계수는 대부분 0이 아니며 평균 크기는 2.2인 반면, $D_0$의 detail 계수의 평균 크기는 0에 훨씬 더 가깝다.
- $D_2$의 대부분 계수는 중요하지 않다. 역 웨이블릿 변환에서 이를 0으로 설정함으로써 99.64% IoU로 TSDF를 충실하게 재구성할 수 있다.
Subband 계수 필터링
위의 결과를 바탕으로, 전처리로서 subband 계수 필터링 접근법을 도입하여 충실하고 컴팩트한 wavelet-tree 표현을 구축한다.
- $C_0$: 모든 계수를 보존
- $D_2$: 모든 계수를 삭제
- $D_0$, $D_1$: 가지고 있는 정보에 따라 선택적으로 유지
- $D_0$의 서브밴드에서 각 좌표를 평가하여 ‘정보’ 척도로 가장 큰 크기를 가진 좌표를 선택
- 상위 $K = 16384$개의 정보 좌표 $X_0$와 이와 연관된 형제 계수 $D_0^\prime$만 유지
- $X_0$가 주어지면 각 위치에서 $D_1$의 $(2^d − 1) 2^d$개의 자식을 유지하고 나머지 덜 중요한 계수를 버림으로써 정보가 풍부한 또 다른 계수 집합 $D_1^\prime$을 생성
위의 절차는 $C_0$, $X_0$, $D_0^\prime$, $D_1^\prime$의 네 부분으로 구성된 wavelet-tree 표현을 생성한다. 이는 상당한 압축 (크기를 1/15로 줄임)과 인상적인 평균 IoU 99.56%를 달성할 뿐만 아니라 스트리밍과 로딩 속도를 44.5% 향상시켜 대규모 학습에 중요하다. 특히 이 프로세스는 일회성 전처리 단계이므로 수백만 개의 3D shape을 처리하고 클라우드에 저장하는 데 효율적이다.
2. Diffusable Wavelet-tree Representation
위의 표현은 데이터 스트리밍에는 효율적이지만, 규칙적인 구조($C_0$)와 불규칙한 구조($X_0$, $D_0^\prime$, $D_1^\prime$)가 혼합되어 diffusion model을 학습하는 동안에는 여전히 어려움이 있다.
간단한 방법 중 하나는 multi-branch 네트워크를 사용하여 이를 diffusion 대상으로 직접 처리하는 것이다. 그러나 이 방법은 수렴 문제를 나타내어 모델 학습이 붕괴된다.
두 번째 방법은 $D_0^\prime$, $D_1^\prime$을 로드하여 좌표에 따라 $D_0$, $D_1$과 같은 크기의 0으로 초기화된 볼륨에 다시 할당하는 것이다. 그러면 파생된 볼륨 \(\hat{D}_0 \in \mathbb{R}^{(2^d - 1) \times 46^3}\), \(\hat{D}_1 \in \mathbb{R}^{(2^d - 1) \times (2^d) \times 46^3}\)을 공간 해상도가 큰 그리드에 단순하게 배열할 수 있다. 그러나 diffusion model에 일반적으로 사용되는 U-Net 아키텍처를 이러한 공간적으로 큰 구조에 사용하면 메모리 집약적인 feature map이 생성되어 메모리 부족 문제가 발생하고 GPU 활용이 비효율적으로 발생한다.
Subband 계수 패킹
\(\hat{D}_1\)을 reshape하여 $C_0$, \(\hat{D}_0\)과 동일한 공간 해상도인 $46^3$을 가질 수 있도록 $(2^d − 1)(2^d)$개의 채널을 갖도록 한다. 그런 다음, 채널 차원에서 $C_0$, \(\hat{D}_0\), reshape된 \(\hat{D}_1\)을 concat하여 diffusion 가능한 wavelet-tree 표현 $x_0 \in \mathbb{R}^{2^{2d} \times 46^3}$을 사용한다. 이 전략은 대략적으로 세제곱 차수의 속도 향상을 가져오며, 동일한 네트워크 아키텍처에 적용했을 때 약 64배의 GPU 메모리 사용량 감소를 기대할 수 있다.
3. Subband Adaptive Training Strategy
$x_0$를 생성하기 위해 diffusion model $f_\theta (x_t, t)$를 학습시킨다. DDPM에 따라 $x_0$에 MSE loss를 직접 적용하면 $C_0$, \(\hat{D}_0\)및 \(\hat{D}_1\)의 불균형한 채널 차원으로 인해 불균형한 loss 가중치가 발생할 수 있다. 게다가, 이 세 볼륨에 동일한 loss 가중치를 할당하더라도 성능이 여전히 만족스럽지 않다.
이러한 문제를 해결하기 위해, 나머지 detail 계수들과 균형을 유지하면서 진폭이 큰 detail 계수를 우선시하는 subband 적응형 학습 전략을 도입한다.
\(\hat{D}_{0,j}\)를 \(\hat{D}_0\)의 subband 중 하나라고 하면, 정보가 풍부한 좌표 세트 \(Y_{0,j}\)를 선택한다.
\[\begin{equation} Y_{0,j} = \{y \vert y \in \hat{D}_{0,j}, \hat{D}_{0,j}[y] > \max (\hat{D}_{0,j})/32\} \end{equation}\]그런 다음 모든 subband의 좌표 세트를 \(Y_0 = \cup_{j=0}^{2^d - 1} Y_{0,j}\)로 합친다. 여기에는 중요한 detail 계수의 위치가 기록된다. \(\hat{D}_1\)의 경우, $Y_0$를 가장 유익한 좌표로 채택한다.
Loss는 다음과 같다.
\[\begin{equation} L_\textrm{MSE} (C_0) + \frac{1}{2} \sum_{i \in \{0,1\}} \sum_{j=0}^{2^d - 1} [L_\textrm{MSE} (\hat{D}_{i,j} [Y_0]) + L_\textrm{MSE} (\hat{D}_{i,j} [Z_0])] \end{equation}\](\(\hat{D}_{i,j} [Y_0]\)는 \(\hat{D}_{i,j}\)의 정보가 풍부한 계수, $Z_0$는 여집합 \(\hat{D}_0 \backslash Y_0\)에서 무작위로 샘플링된 부분집합)
$Z_0$의 크기가 $Y_0$의 크기와 같도록 보장하여 이러한 좌표에서 네트워크 예측에 대한 supervision을 제공하며, 이 접근 방식은 덜 중요한 계수가 동일한 양의 supervision을 받도록 보장한다.
효율적인 loss 계산
PyTorch에서 효율적인 코드 컴파일을 위해 고정 크기의 바이너리 마스크를 사용하여 좌표 집합을 표현한다. 이를 통해 생성 대상과 네트워크 예측을 모두 마스킹하여 MSE loss를 계산할 수 있으므로 불규칙한 연산이 필요 없다.
4. Conditional Generation
본 논문의 프레임워크는 다양한 모달리티에 걸쳐 조건부 생성을 수용하도록 확장될 수 있다. 이를 달성하기 위해 주어진 조건을 일련의 latent 벡터로 변환하는 각 모달리티에 대해 서로 다른 인코더를 사용한다. 그런 다음 이러한 벡터는 여러 컨디셔닝 메커니즘을 사용하여 생성기에 주입된다. 또한 더 큰 효과를 경험적으로 입증한 classifier-free guidance 메커니즘을 사용한다.
Experiments
- 데이터셋: ModelNet, ShapeNet, SMPL, Thingi10K, SMAL, COMA, House3D, ABC, Fusion 360, 3D-FUTURE, BuildingNet, DeformingThings4D, FG3D, Toys4K, ABO, Infinigen, Objaverse, ObjaverseXL (Thingiverse and GitHub)
- 학습 디테일
- optimizer: Adam
- learning rate: 0.0001
- batch size: 96
- exponential moving average: 0.9999
- iteration: 입력 조건에 따라 200만 ~ 400만
- GPU: A10G 48개
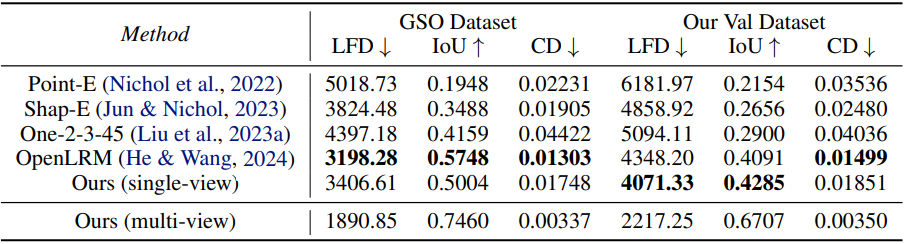
1. Quantitative Comparison with Existing Large Generative Models
다음은 image-to-3D 성능을 다른 방법들과 비교한 것이다.

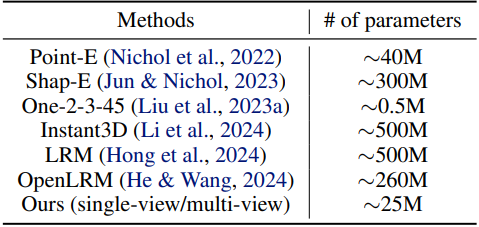
다음은 모델의 파라미터 수를 비교한 표이다.
2. Conditional generation
다음은 단일 이미지를 조건으로 생성한 예시들이다.

다음은 멀티뷰 이미지를 조건으로 생성한 예시들이다.

다음은 포인트 클라우드를 조건으로 생성한 예시들이다.

다음은 voxel을 조건으로 생성한 예시들이다.

3. 3D Shape Completion
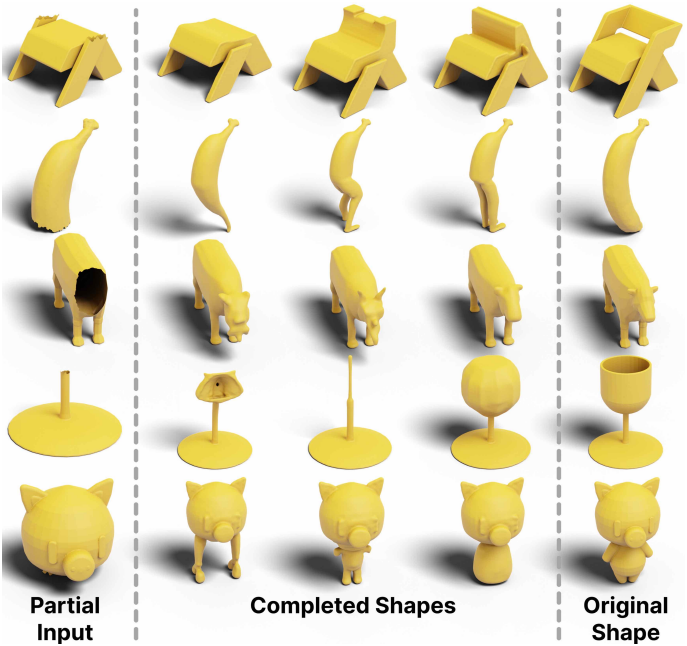
다음은 부분적인 3D 입력으로부터 zero-shot으로 완전한 3D shape을 생성한 예시들이다.
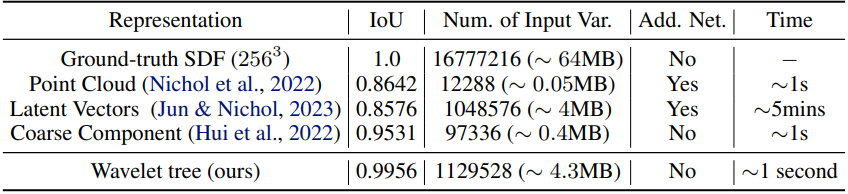
4. Ablation Studies
다음은 ablation 결과이다.