[논문리뷰] Reconstructing and Simulating Dynamic 3D Objects with Mesh-adsorbed Gaussian Splatting

arXiv 2024. [Paper] [Page]
Shaojie Ma, Yawei Luo, Yi Yang
Zhejiang University
3 Jun 2024

Introduction

3D 재구성과 3D 시뮬레이션은 서로 관련이 있지만 뚜렷한 목적이 있다. 재구성에는 다양한 장면에 적응할 수 있는 유연한 3D 표현이 필요한 반면 시뮬레이션에는 변형을 효과적으로 모델링하기 위한 구조화된 표현이 필요하다. 이러한 이중 요구 사항은 통합 프레임워크에 상당한 과제를 안겨준다.

본 논문은 이를 해결하기 위해 Mesh-adsorbed Gaussian Splatting (MaGS)을 제안하였다. MaGS는 3D Gaussian이 메쉬 표면에 떠 있도록 제한하여 3D Gaussian의 렌더링 유연성과 메쉬의 공간적 일관성을 결합한 하이브리드 메쉬-Gaussian 3D 표현을 만든다.

메쉬 변형 외에도 메쉬와 Gaussian 간의 상대적 움직임을 모델링하기 위한 학습 가능한 Relative Deformation Field (RDF)를 추가로 제안하였다. 이러한 설계는 일반적으로 메쉬와 Gaussian의 상대적 위치가 고정된 다른 방법과 다르다. 학습 가능한 RDF를 통해 메쉬와 3D Gaussian 간의 상대적 변위를 허용함으로써 MaGS는 동적 물체 재구성 중 렌더링 정확도와 변형 합리성 간의 trade-off를 피하였다.

시뮬레이션 측면에서 MaGS는 메쉬 내에서 as-rigid-as-possible (ARAP) prior를 확장하여 각 3D Gaussian의 상대적 동작을 캡처하여 더 복잡한 변형을 처리한다. 메쉬, 3D Gaussian, RDF를 공동 최적화함으로써 MaGS는 높은 렌더링 정확도와 사실적인 변형을 모두 달성하였다.

Methodology

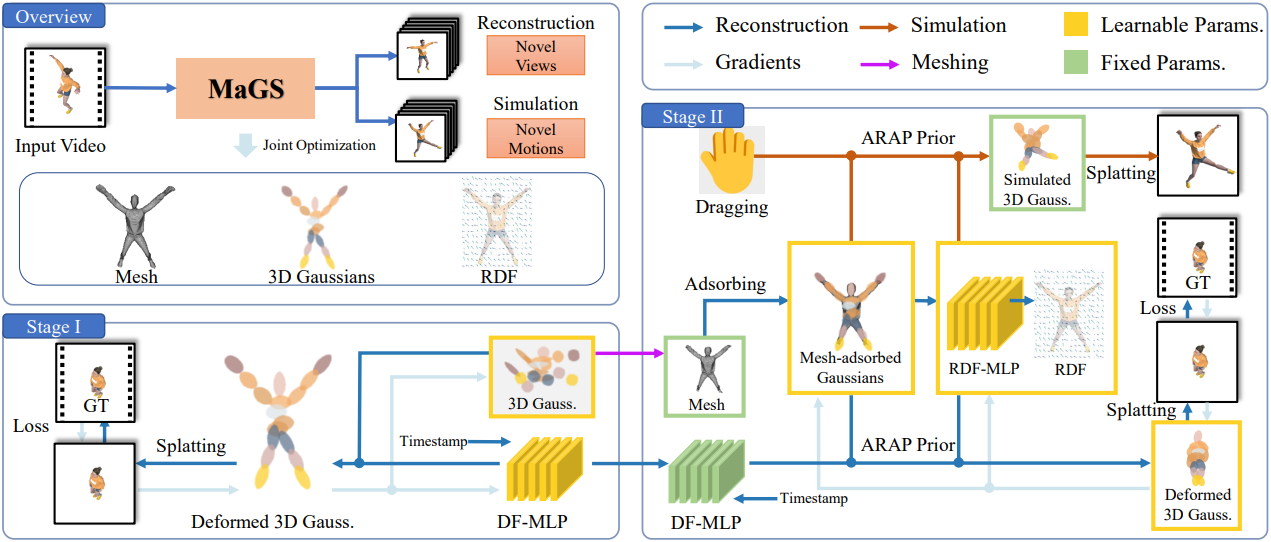
1. Stage I: Mesh Extraction and Deformation Field Estimation

1단계에서는 동영상(monocular)에서 동적 물체의 대략적인 모양과 변형을 모델링하는 것으로 시작한다. 구체적으로, 3D Gaussian을 무작위로 초기화하고 deformation field를 사용하여 각 Gaussian의 시간적 변화를 나타낸다. DF-MLP라 부르는 MLP를 사용하여 0번째 프레임에서 $t$번째 프레임까지 이러한 deformation field를 예측한다. 시간 0에서의 초기 Gaussian $G_g$에 대해 3D Gaussian을

\[\begin{equation} \{G_g (T = 0) : \mu_g, q_g, s_g, \sigma_g, c_g\} \end{equation}\]

로 정의한다. 시간 $t$에서 deformation field는 변화를 예측하는 데 도움이 된다.

\[\begin{equation} (\delta \mu, \delta q, \delta s, \delta \sigma, \delta c) = \mathcal{D} (\mathcal{E}_p (\mu_g), \mathcal{E}_t (t)) \end{equation}\]

(\(\mu_g\)는 시간 0에서의 Gaussian의 평균, $\mathcal{E}$는 시간과 좌표를 임베딩하는 함수)

예측된 변형은 초기 3D Gaussian에 적용되어 시간 $t$에서의 Gaussian을 얻으며, 그 결과

\[\begin{equation} \{G_g (T = t) : \mu_g + \delta \mu, q_g \times \delta q, s_g + \delta s, \sigma_g + \delta \sigma, c_g + \delta c\} \end{equation}\]

가 된다. 변형된 Gaussian은 스플래팅을 사용하여 렌더링되고, Gaussian 파라미터와 DF-MLP를 최적화하기 위해 렌더링된 뷰와 GT 동영상 프레임 간의 loss가 계산된다.

3D Gaussian에서 대략적인 메쉬를 설정하기 위해 SuGaR를 사용한다. SuGaR는 3D Gaussian에서 렌더링한 depth map에서 포인트 클라우드를 추정한 다음 재구성을 위해 Marching Cubes 알고리즘을 적용한다.

2. Stage II: Mesh-adsorbed Gaussian Splatting

Mesh-adsorbed Gaussian

메쉬와 3D Gaussian 간의 연결을 설정하기 위해 Mesh-adsorbed 3D Gaussian 표현을 도입하였다. 삼각형 메쉬 기반을 활용하는데, 여기서 초기 메쉬 $M$의 각 면 $m$은 vertex \(v_{1..3} \subset \mathbb{R}^3\)으로 구성된다. 변형되지 않은 원래 Mesh-adsorbed Gaussian의 경우 3D Gaussian의 중심이 메쉬에 위치하도록 초기화하고 다음 공식을 사용하여 $m$에 흡착된 Gaussian $g$의 $\mu$를 계산한다.

\[\begin{equation} \mu = \frac{v_1 \times \mathcal{F}(\alpha_1) + v_2 \times \mathcal{F} (\alpha_2) + v_3 \times \mathcal{F} (\alpha_3)}{\mathcal{F} (\alpha_1) + \mathcal{F} (\alpha_2) + \mathcal{F} (\alpha_3)} \\ \textrm{where} \; \mathcal{F} (x) = \frac{1}{e^{-x} + 1} \in (0, 1) \end{equation}\]

여기서 \(\alpha_{1..3} \subset \mathbb{R}^3\)은 메쉬에서 Gaussian의 배치를 지시하는데, 랜덤한 값으로 초기화된 학습 가능한 파라미터이다. 이 표현은 Gaussian이 메쉬 중심 근처에 흡착되고 학습을 통해 상대적 위치가 반복적으로 변경되도록 한다. $\alpha$는 렌더링 정확도를 개선하기 위해 3D Gaussian을 정확하게 배치하도록 최적화된다.

다른 방법과 달리, MaGS는 메쉬가 변형될 때 3D Gaussian이 면에 고정되지 않고 그 위에 떠 있을 수 있도록 한다. 적응적 호버링을 위해, RDF를 사용하여 메쉬가 변형될 때 메쉬에서 Gaussian의 호버링을 나타내는 위치에 따른 값 \(\Delta_\alpha\)와 \(\Delta_\mu\)를 계산한다. 변형된 Mesh-adsorbed Gaussian의 경우 $\mu$를 계산할 때 다음과 같이 호버링을 고려해야 한다.

\[\begin{equation} \mu = \frac{v_1 \times \mathcal{F} (\alpha_1^\prime) + v_2 \times \mathcal{F} (\alpha_2^\prime) + v_3 \times \mathcal{F} (\alpha_3^\prime)}{\mathcal{F} (\alpha_1^\prime) + \mathcal{F} (\alpha_2^\prime) + \mathcal{F} (\alpha_3^\prime)} + \Delta_\mu \\ \textrm{where} \; \alpha_i^\prime = \alpha_i + \Delta_{\alpha_i} \end{equation}\]

또한 Gaussian의 모양은 변형 중에 변경된다. 변형 전후의 $m$의 면적 변화 비율에 따라 $g$의 scaling $s_g$를 업데이트한다.

\[\begin{equation} s_g^\prime = s_g \cdot \frac{\vert (v_2^\prime - v_1^\prime) \times (v_3^\prime - v_1^\prime) \vert}{\vert (v_2 - v_1) \times (v_3 - v_1) \vert} \end{equation}\]

($v$와 $v^\prime$은 각각 변형 전과 변형 후 $m$의 vertex, $s_g^\prime$은 변형 후의 scaling 파라미터)

Rotation $q_g$의 경우, Gram-Schmidt process를 사용하여 변형 전후 메쉬의 orthogonal basis $\mathcal{O}$와 $\mathcal{O}^\prime$를 계산한다.

\[\begin{aligned} \mathcal{O} &= \textrm{GramSchmidt} (v_2 - v_1, v_3 - v_1, (v_2 - v_1) \times (v_3 - v_1)) \\ \mathcal{O}^\prime &= \textrm{GramSchmidt} (v_2^\prime - v_1^\prime, v_3^\prime - v_1^\prime, (v_2^\prime - v_1^\prime) \times (v_3^\prime - v_1^\prime)) \end{aligned}\]

그런 다음 $\mathcal{O}$를 $\mathcal{O}^\prime$로 상대적으로 변환하는 rotation $R^\ast$를 계산한다. 업데이트된 rotation은 \(q_g^\prime = q_g R^\ast\)로 계산된다.

전체 프로세스가 미분 가능하므로 렌더링 오차의 역전파를 통해 메쉬와 메쉬에 붙은 3D Gaussian을 함께 최적화할 수 있다.

Local-Rigid Deformation (Mesh Deformation)

DF-MLP의 가중치 형태로 제시된 1단계에서 얻은 변형 정보는 대략적이고 부정확하다. 제약 조건이 없기 때문에 변형 네트워크가 특정 위치에서 매끄럽지 않아 변형 중에 특정 위치의 점이 불연속적으로 발생한다. 이 정보를 사용하여 Mesh-adsorbed Gaussian들을 직접 가이드하여 변형하면 좋은 결과를 얻을 수 없다.

이 문제를 해결하기 위해 먼저 Mesh-adsorbed Gaussian들의 현재 메쉬에 Poisson disk sampling을 적용하여 균일하게 분포된 핸들 세트를 얻는다. 변형 중에 핸들과 타겟 타임스탬프 $t$를 DF-MLP로 전달하여 핸들들의 변형된 위치를 얻는다. 그런 다음 ARAP를 사용하여 나머지 다른 점들의 위치를 계산한다.

변형 전후의 핸들 좌표는 ARAP 알고리즘에 입력된다. ARAP 방법은 local rigid transformation을 허용하면서 메쉬 면들의 왜곡을 최소화하여 변형된 메쉬를 계산한다. 이는 이웃 vertex 간의 상대 거리를 가능한 한 보존하는 일련의 최적화 문제를 해결하여 달성된다. 구체적으로 ARAP 에너지 함수는 다음과 같이 정의된다.

\[\begin{equation} E_\textrm{ARAP} (V^\prime) = \sum_{i=1}^n \sum_{(i,j) \in E} \| (V_i^\prime - V_j^\prime) - R_i (V_i - V_j) \|^2 \end{equation}\]

($V$는 원래 vertex 위치, $V^\prime$는 변형된 vertex 위치, $E$는 edge 집합, $R_i$는 vertex $i$에 가장 적합한 rotation matrix)

이 방법을 통해 대략적인 변형 정보만 제공하는 변형 네트워크에 대한 의존도를 줄여 최종 결과에 미치는 오차의 영향을 줄인다.

Relative Deformation Fields (3D Gaussians Deformation)

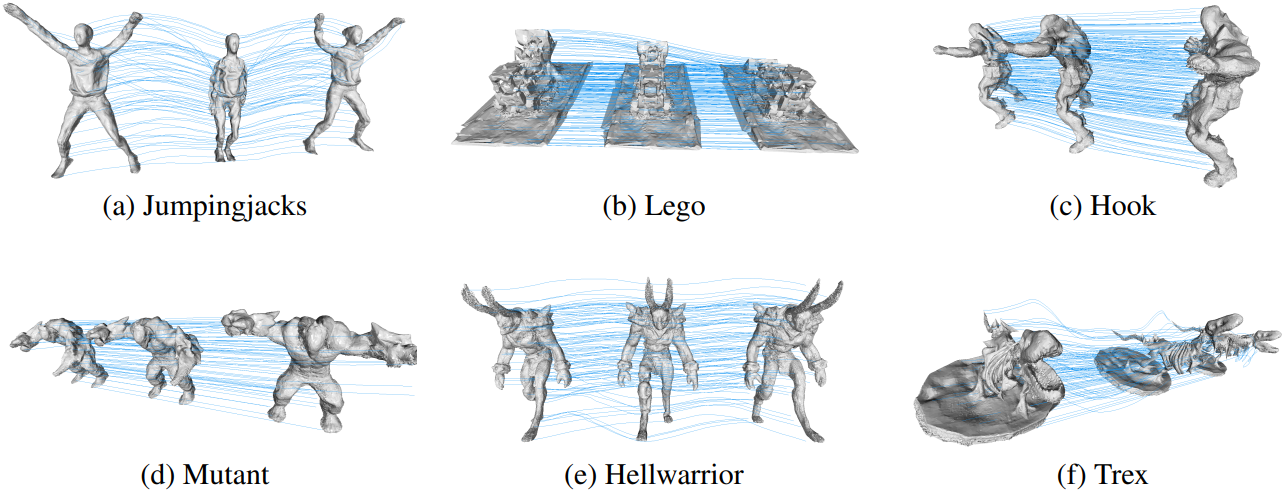
ARAP deformation을 적용하면 메쉬가 비교적 자연스러운 동작을 얻을 수 있지만, ARAP는 local rigidity 가정에 의존한다. 실제 시나리오에서는 종종 이 가정을 엄격히 준수하지 않아 렌더링 중에 정확도를 떨어뜨릴 수 있는 불일치가 발생한다. 이 문제를 해결하기 위해 학습 가능한 relative deformation field (RDF)를 도입하여 다양한 물체에서 각 3D Gaussian에 대해 보다 정확한 동작 모델링을 가능하게 한다.

RDF-MLP는 메쉬의 인코딩된 인덱스, 변형된 메쉬 좌표, 메쉬의 상대적 Gaussian 위치를 입력으로 사용하고, \(\Delta_\alpha\)와 \(\Delta_\mu\)를 출력한다. 이러한 조정을 통해 Gaussian은 고정되지 않고 변형된 메쉬에서 동적으로 호버링할 수 있으므로 메쉬 변형 프로세스의 적응성과 정확성이 향상된다.

네트워크 최적화 시에는 예측된 Gaussian 위치와 메쉬에서의 실제 위치 간의 차이를 최소화하여 non-rigid deformation field가 물체의 실제 동작을 정확하게 반영하도록 한다.

3. User-interactive Simulation

MaGS는 메쉬를 직접 수정하여 사용자 상호 작용 시뮬레이션 (ex. 드래그)을 가능하게 하며, 이를 통해 흡착된 3D Gaussian이 업데이트되어 빠른 렌더링이 가능하다.

1. ARAP 알고리즘을 사용하여 사용자의 동작에 따라 메쉬를 대략적으로 변형한다. 3D Gaussian은 이 변형을 따른다.
2. 변형된 Mesh-adsorbed Gaussian의 파라미터를 RDF-MLP에 입력하여 RDF를 얻고, 이를 통해 3D Gaussian의 위치를 ​​더 정밀하게 조정한다.

이러한 점진적 변형을 통해 MaGS는 물체 표현의 충실도를 유지하여 복잡한 변형에도 합리적이고 유연한 편집이 가능하다.

Experiments

• 데이터셋: D-NeRF, NeRF-DS

1. Quantitative Comparisons

다음은 합성 데이터셋에서의 정량적 평가 결과이다.

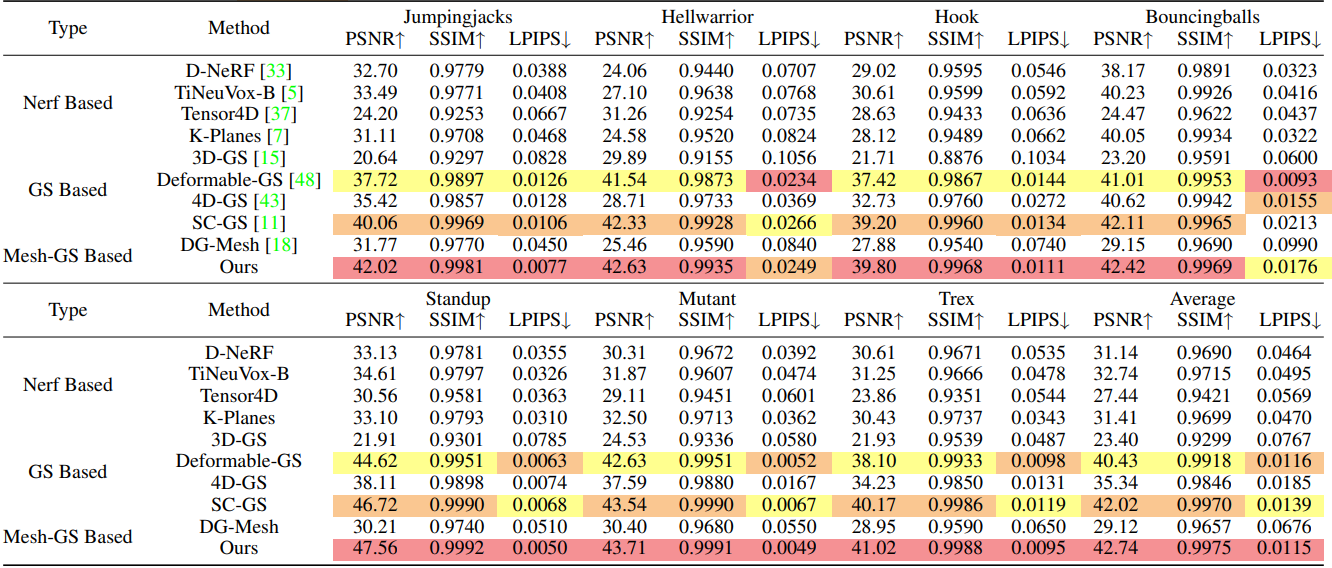
2. Qualitative Comparisons

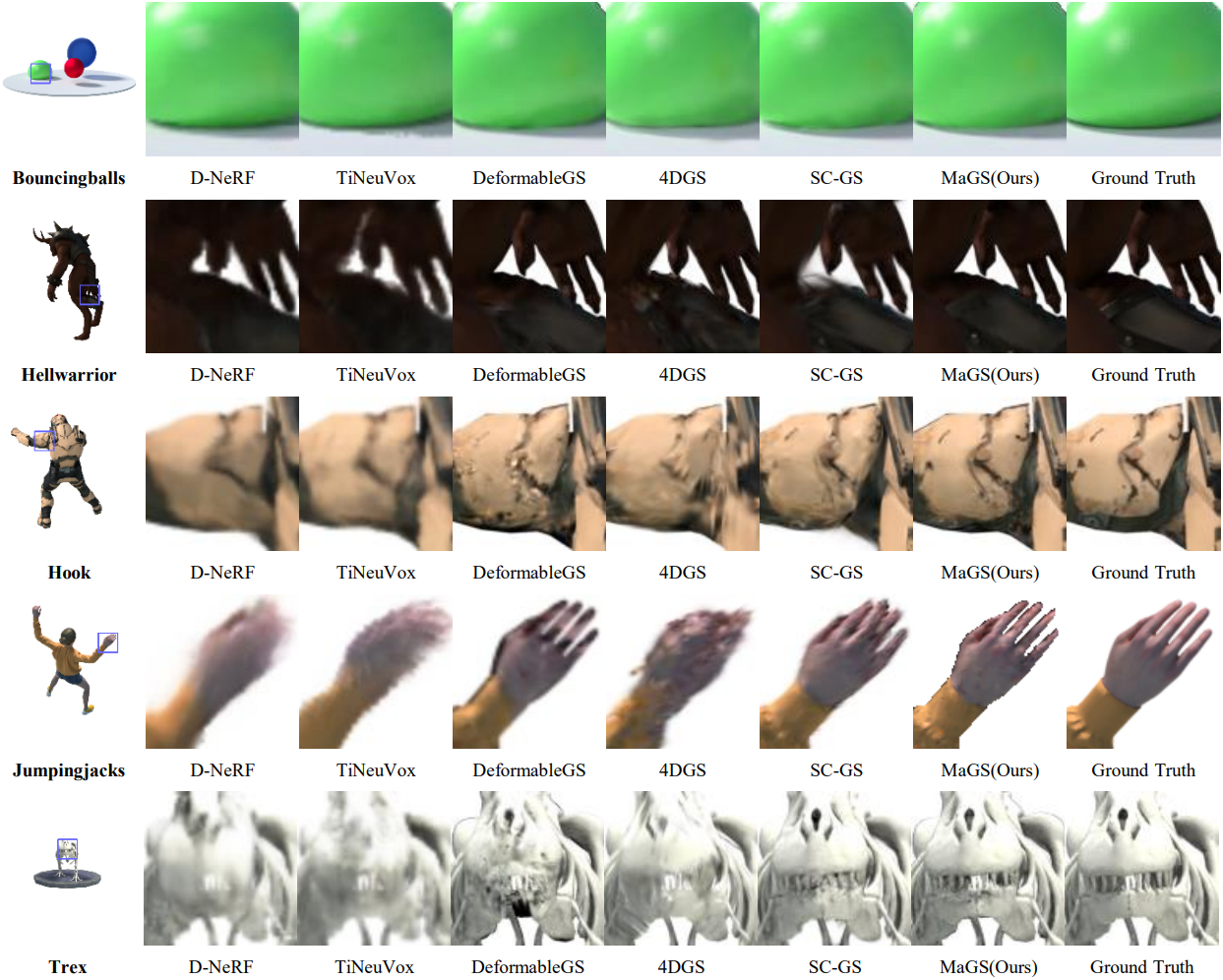
다음은 D-NeRF 데이터셋에서 정성적으로 비교한 결과이다. (렌더링 해상도: 800$\times$800)

다음은 드래그를 이용한 사용자 상호작용 편집 결과이다.

3. Ablation Studies

다음은 D-NeRF 데이터셋에서의 ablation 결과이다.