[논문리뷰] Masked Autoencoders Are Effective Tokenizers for Diffusion Models

ICML 2025 (Spotlight). [Paper] [Github]
Hao Chen, Yujin Han, Fangyi Chen, Xiang Li, Yidong Wang, Jindong Wang, Ze Wang, Zicheng Liu, Difan Zou, Bhiksha Raj
Carnegie Mellon University | AMD | The University of Hong Kong | Peking University | William & Mary
5 Feb 2025

Introduction

Diffusion model을 위한 좋은 latent space는 무엇일까? 초기 논문들에서는 주로 tokenizer로 VAE를 사용했는데, 이는 학습된 latent 코드가 KL 제약을 통해 비교적 매끄러운 분포를 따르도록 보장한다. VAE는 강력한 생성 결과를 제공할 수 있지만, 부과된 정규화로 인해 재구성에서 높은 픽셀 수준의 충실도를 달성하는 데 어려움을 겪는 경우가 많다. 반면, 일반 오토인코더(AE)를 사용한 최근의 방법들은 더 높은 충실도의 재구성을 생성하지만, 다운스트림 생성 task에 대해 충분히 구성되지 않았거나 너무 얽힌 latent space를 생성할 수 있다. 사전 학습된 모델로 latent 정렬을 활용하면 생성 성능을 더욱 향상시킬 수 있는 경우가 많다.

본 논문에서는 tokenizer가 학습한 latent 분포와 해당 latent space에서 작동하는 diffusion model의 학습 및 샘플링 동작 간의 상호작용을 조사하여 이 질문에 대한 답을 찾고자 한다. 구체적으로, 저자들은 Gaussian mixture model (GMM)을 latent space에 적용하여 AE, VAE, 그리고 최근 등장한 표현 정렬된 VAE를 연구하였다. 경험적으로, GMM mode가 적고 판별력이 더 뛰어난 feature를 가진 latent space가 diffusion loss를 감소시키는 경향이 있다. 이론적으로, GMM mode가 적은 latent 분포가 실제로 diffusion model의 loss를 줄이고 inference 과정에서 샘플링을 개선한다.

본 논문은 판별력이 뛰어난 latent space를 가진 AE에 대해 학습된 diffusion model이 SOTA 성능을 달성하기 때문에, AE를 Masked Autoencoder (MAE)로 학습시키는 것을 제안하였다. 구체적으로, tokenizer로 transformer 아키텍처를 채택하고, 인코더에서 이미지 토큰을 랜덤하게 마스킹한다. 이 토큰의 feature는 디코더에서 재구성되어야 한다. 높은 재구성 충실도를 가진 픽셀 디코더를 유지하기 위해, 일반적으로 이전 tokenizer로 학습되는 픽셀 디코더와 함께, 보이지 않는 토큰의 feature를 보이는 토큰에서 예측하여 표현을 학습하는 얕은 보조 디코더를 채택하였다. 얕은 보조 디코더는 학습 중에 사소한 계산 오버헤드를 발생시킨다. 이 디자인을 사용하면 마스킹된 이미지 패치를 재구성하는 MAE loss를 확장하여 HOG feature, DINOv2 feature, CLIP 임베딩, 텍스트가 포함된 BPE 인덱스 등 여러 타겟들을 동시에 예측할 수 있다.

또한 저자들은 흥미로운 분리 효과를 발견했다. 인코더에서 판별력이 뛰어나고 semantic하게 풍부한 latent space를 학습하는 능력과 디코더에서 높은 재구성 충실도를 달성하는 능력이 분리될 수 있다는 것이다. 특히, MAE 학습에서 높은 마스킹 비율은 즉각적인 픽셀 수준 품질을 저하시키는 경우가 많다. 그러나 AE의 인코더를 고정시켜 잘 정리된 latent space를 보존하고 디코더만 fine-tuning함으로써, 학습된 표현의 semantic 이점을 희생하지 않고도 강력한 픽셀 수준 재구성 충실도를 회복할 수 있다.

MAETok은 마스크 모델링을 사용하여 일반 AE를 학습함으로써 재구성 충실도와 판별력 있는 latent space 간의 상충 관계를 해결하였다. 이는 latent space의 구조가 VAE보다 diffusion 학습에 더 중요함을 보여준다. MAETok은 256$\times$256 및 512$\times$512 ImageNet 벤치마크에서 단 128개의 토큰만을 사용하여 향상된 rFID와 gFID를 달성하였다.

On the Latent Space and Diffusion Models

경험적 분석

Latent space와 생성 품질 간의 연관성에 대한 연구는 높은 수준의 직관에서 시작되었다. 최적의 diffusion model 파라미터와 tokenizer 디코더의 유사한 용량을 가정할 때, diffusion model의 생성 품질, 즉 학습된 latent 분포는 denoising 네트워크의 학습 loss에 의해 지배되는 반면, DDPM을 통한 diffusion model 학습의 효과는 latent space 분포 학습의 어려움에 크게 좌우된다. 특히, 학습 데이터 분포가 너무 복잡하고 충분히 판별력이 없는 경우, denoising 네트워크는 latent space의 이러한 얽힌 구조를 포착하는 데 어려움을 겪을 수 있으며, 결과적으로 생성 품질이 저하된다.

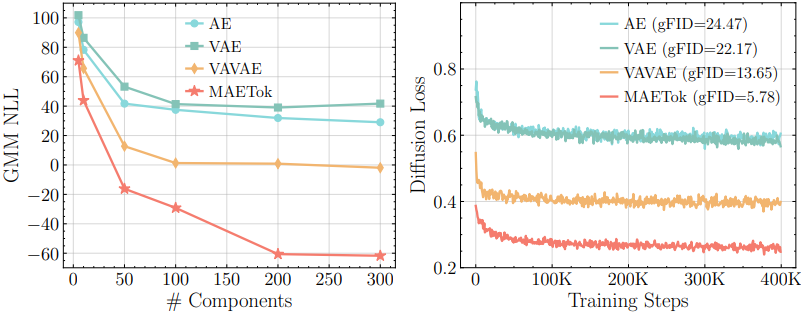
이러한 직관을 바탕으로, 저자들은 Gaussian mixture model (GMM)을 사용하여 latent space 표현의 mode 수를 평가하였다. 여기서 mode 수가 많을수록 구조가 더 복잡함을 나타낸다. 위 그림은 Gaussian 수에 따른 NLL과 diffusion loss를 비교한 결과이다. NLL이 낮을수록 피팅 품질이 더 우수함을 나타내며, mode 수가 적을수록 diffusion loss가 적고 gFID가 더 우수하다. 이를 통해 mode 수가 적고 따라서 더 분리되고 구별되는 feature를 가진 latent space가 학습 난이도를 줄이고 diffusion model의 생성 품질을 향상시킬 수 있음을 알 수 있다.

이론적 분석

데이터 분포를 $K$개의 Gaussian의 혼합으로 가정하자.

\[\begin{equation} p_0 = \frac{1}{K} \sum_{i=1}^K \mathcal{N} (\boldsymbol{\mu}_i^\ast, \textbf{I}) \end{equation}\]

각 mode의 norm이 어떤 상수 $B$로 제한된다고 가정하고, $d$를 데이터 차원, $T$를 총 timestep, $\epsilon$을 적절한 타겟 오차 파라미터라 하자. 데이터 분포와 생성 분포 사이의 KL divergence에서 $O(T \epsilon^2)$ 오차를 달성하기 위해, DDPM 알고리즘은 적어도 $n$개의 샘플을 사용해야 한다.

\[\begin{equation} n = \Theta \left(\frac{K^4 d^5 B^6}{\epsilon^2}\right), \quad \textrm{where} \; \max_i \| \boldsymbol{\mu}_i \| \le B \end{equation}\]

비교 가능한 생성 품질 O(T ϵ2 )을 달성하려면 mode가 더 많은 latent space가 더 큰 학습 샘플 크기를 필요로 하며, 이는 $O(K^4)$로 확장된다. 이는 유한한 수의 학습 샘플에서 mode가 더 많은 latent space가 더 나쁜 생성 결과를 생성하는 이유를 이론적으로 설명하는 데 도움이 된다. Latent space들의 분포는 비슷한 상한 $B$를 공유하며, 따라서 mode 수 $K$에 주로 영향을 받는다.

Method

VAE는 diffusion model에 반드시 필요하지 않을 수 있으며, 단순한 AE만으로도 판별 가능한 latent space로 인해 128개 토큰만으로 SOTA 생성 성능을 달성하기에 충분하다.

1. Architecture

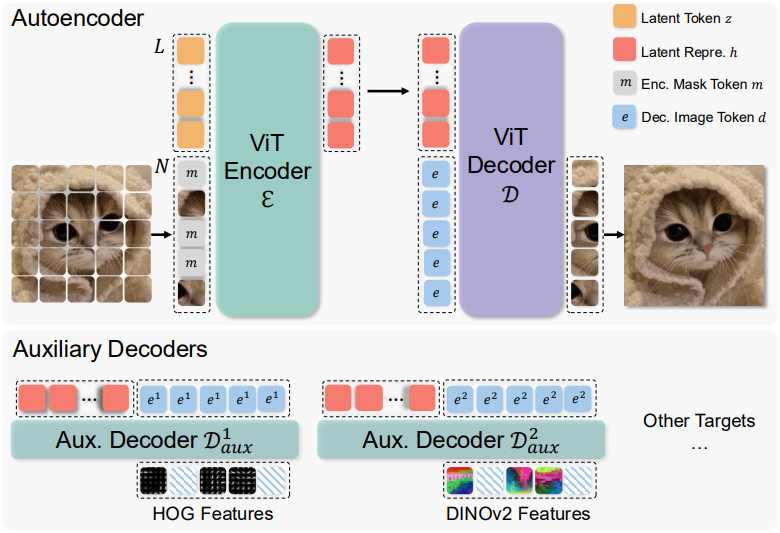
저자들은 학습 가능한 latent 토큰을 사용하는 최신 1D tokenizer 디자인을 기반으로 MAETok을 구축했다. 인코더 $\mathcal{E}$와 디코더 $\mathcal{D}$는 모두 ViT 아키텍처를 채택하지만, 이미지 토큰과 잠재 토큰을 모두 처리하도록 설계되었다.

인코더

인코더는 먼저 입력 이미지 $I \in \mathbb{R}^{H \times W \times 3}$을 미리 정의된 패치 크기 $P$에 따라 $N$개의 패치로 나눈다. 각 패치는 차원 $D$의 임베딩 벡터에 매핑되어 이미지 토큰 $\textbf{x} \in \mathbb{R}^{N \times D}$가 된다. 또한, $L$개의 학습 가능한 latent 토큰 $\textbf{z} \in \mathbb{R}^{L \times D}$를 정의한다. 인코더 transformer는 이미지 패치 임베딩과 latent 토큰을 concat하여 입력으로 받고, latent 토큰만으로 차원 $H$의 잠재 표현 $\textbf{h} \in \mathbb{R}^{L \times H}$를 출력한다.

\[\begin{equation} \textbf{h} = \mathcal{E} ([\textbf{x}; \textbf{z}]) \end{equation}\]

디코더

이미지를 재구성하기 위해 $N$개의 학습 가능한 이미지 토큰 집합 $\textbf{e} \in \mathbb{R}^{N \times H}$를 사용한다. 이 마스크 토큰들을 디코더의 입력으로 $\textbf{h}$와 concat하고, 마스크 토큰의 출력만 사용하여 재구성한다.

\[\begin{equation} \hat{\textbf{x}} = \mathcal{D}([\textbf{e}; \textbf{h}]) \end{equation}\]

그런 다음 $\hat{\textbf{x}} \in \mathbb{R}^{N \times D}$에 linear layer를 사용하여 픽셀 값을 예측하고 재구성된 이미지 $\hat{I}$를 얻는다.

위치 인코딩

공간 정보를 인코딩하기 위해, 인코더의 이미지 패치 토큰 $\textbf{x}$와 디코더의 이미지 토큰 $\textbf{e}$에 2D Rotary Position Embedding (RoPE)를 적용한다. 반면, latent 토큰 $\textbf{z}와 이에 대응하는 인코딩된 토큰 $\textbf{h}$는 특정 공간적 위치에 매핑되지 않으므로 표준 1D absolute position embedding을 사용한다. 이러한 디자인은 패치 기반 토큰이 2D 레이아웃 개념을 유지하는 동시에, 학습된 latent 토큰이 transformer 아키텍처 내에서 추상화된 feature 집합으로 처리되도록 한다.

학습 loss

표준 tokenizer loss를 사용하여 MAETok을 학습시킨다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{recon} + \lambda_1 \mathcal{L}_\textrm{percep} + \lambda_2 \mathcal{L}_\textrm{adv} \end{equation}\]

\(\mathcal{L}_\textrm{recon}\), \(\mathcal{L}_\textrm{percep}\), \(\mathcal{L}_\textrm{adv}\)는 각각 pixel-wise MSE loss, perceptual loss, adversarial loss이다. MAETok은 단순한 AE 아키텍처이므로 VAE에서처럼 posterior와 prior 사이의 variational loss가 필요하지 않아 학습이 간소화된다.

2. Mask Modeling

인코더에서의 토큰 마스킹

MAETok의 핵심 속성은 MAE의 원리에 따라 학습 과정에서 마스크 모델링을 도입하여 self-supervised 방식으로 더욱 판별적인 latent space를 학습한다는 것이다. 구체적으로, 바이너리 마스크 $M \in \mathbb{R}^N$에 따라 이미지 패치 토큰의 특정 비율을 랜덤하게 선택하고, 이를 인코더에 입력하기 전에 학습 가능한 마스크 토큰 $m \in \mathbb{R}^D$로 대체한다. 모든 latent 토큰은 마스킹되지 않은 이미지 토큰에 대한 정보를 더욱 집중적으로 집계하기 위해 유지되며, 디코더 출력에서 마스킹된 토큰을 재구성하는 데 사용된다.

얕은 보조 디코더

MAE에서는 마스킹된 이미지 토큰의 목표 feature를 나머지 토큰으로부터 예측하기 위해 얕은 디코더 또는 linear layer가 필요하다. 그러나 MAE를 tokenizer로 학습시키는 것이 목표이므로, 픽셀 디코더 $\mathcal{D}$는 이미지를 높은 충실도로 재구성할 수 있어야 한다. 따라서 $\mathcal{D}$를 $\mathcal{E}$와 유사한 용량으로 유지하고, 얕은 보조 디코더를 통합하여 추가 feature 타겟을 예측한다.

각 보조 디코더 \(\mathcal{D}_\textrm{aux}^j\)는 latent 표현 $\textbf{h}$를 입력으로 받아 자체 $\textbf{e}^j$와 concat하고, feature 타겟 $\textbf{y}^j \in \mathbb{R}^{N \times D^j}$의 재구성인 \(\hat{\textbf{y}}^j\)를 출력한다.

\[\begin{equation} \hat{\textbf{y}}^j = \mathcal{D}_\textrm{aux}^j ([\textbf{e}^j; \textbf{h}]; \theta) \end{equation}\]

마스크 $M$에 따라 마스킹된 토큰에서만 추가적인 MSE loss를 사용하여 AE와 함께 보조 디코더들을 학습시킨다.

\[\begin{equation} \mathcal{L}_\textrm{mask} = \sum_j \| M \otimes (\hat{\textbf{y}}^j - \textbf{y}^j) \|_2^2 \end{equation}\]

3. Pixel Decoder Fine-Tuning

마스크 모델링은 인코더가 더 나은 latent space를 학습하도록 유도하지만, 높은 마스킹 비율은 즉각적인 재구성을 저해할 수 있다. 이를 해결하기 위해 마스크 모델링으로 AE를 학습한 후, 인코더를 고정시켜 latent 표현을 보존하고, 적은 수의 추가 epoch 동안 픽셀 디코더만 fine-tuning한다. 이 과정을 통해 디코더는 깨끗한 이미지의 고정된 latent code에 더욱 잘 적응하여 마스크 학습 중 손실된 디테일을 복구할 수 있다. 이 단계에서는 모든 보조 디코더를 제거한다.

Experiments

• 구현 디테일
  • iteration: 50만
  • $L = 128$, $H = 32$
  • feature 타겟: HOG, DINO-v2-Large, SigCLIP-Large
  • 마스킹 비율: 40% ~ 60%
  • \(\lambda_1 = 1.0\), \(\lambda_2 = 0.4\)
  • 픽셀 디코더 fine-tuning
    • iteration: 5만
    • 마스킹 비율: 60%에서 0%로 선형적으로 감소

1. Design Choices of MAETok

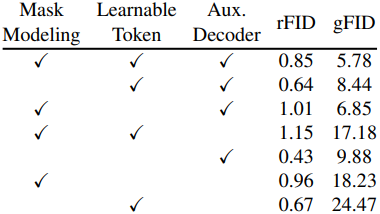
다음은 ImageNet 256$\times$256에서의 ablation 결과이다.

2. Latent Space Analysis

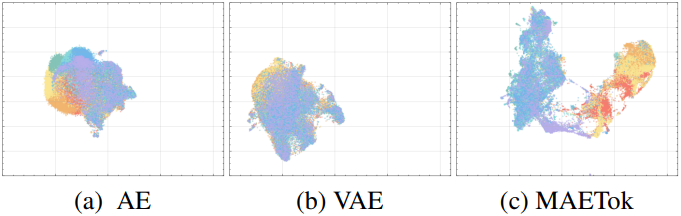
다음은 UMAP으로 학습된 latent space를 시각화하여 비교한 결과이다.

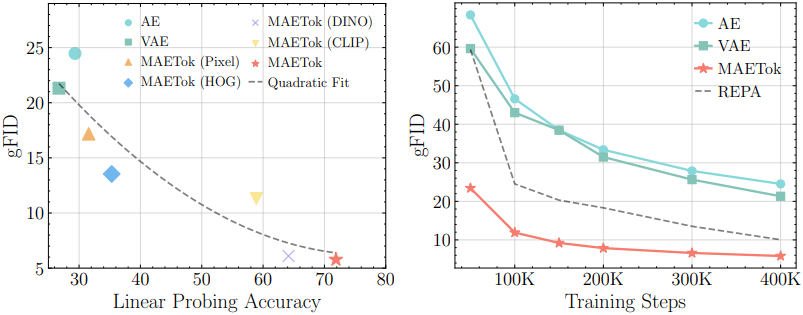
다음은 latent space에 대한 linear probing (LP) 정확도와 gFID를 비교한 결과이다. LP 정확도가 높을수록, 즉 latent space가 더 판별적일수록 diffusion model의 학습이 더 쉽고 더 빠르다.

3. Main Results

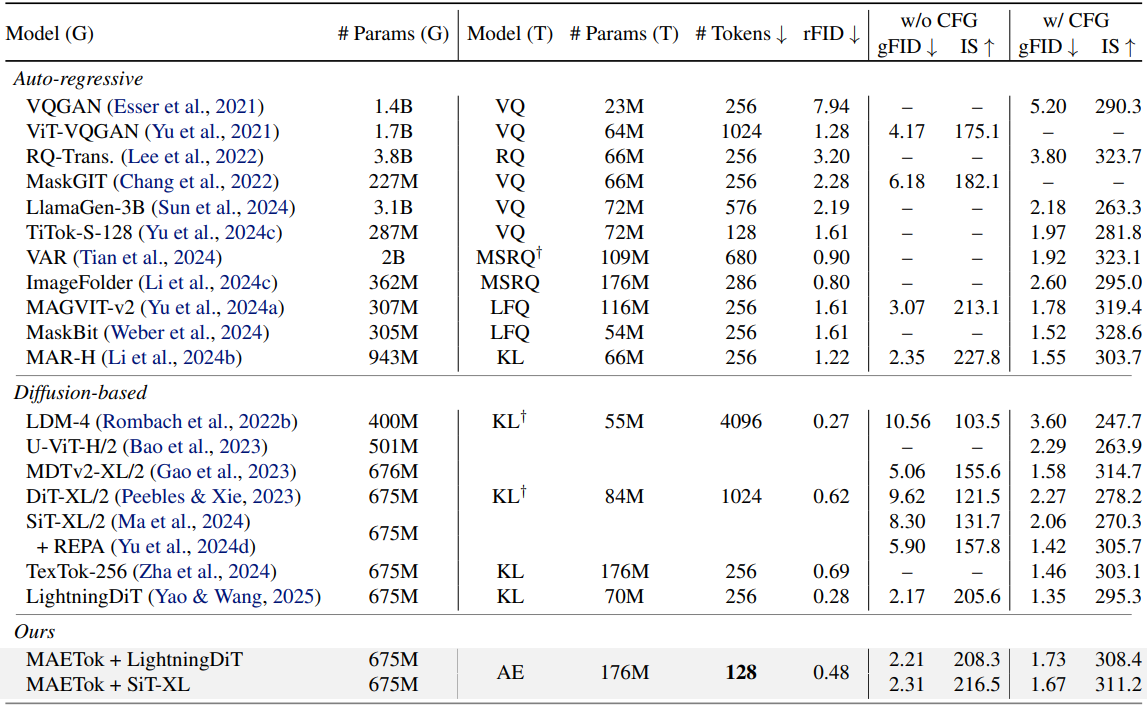
다음은 ImageNet 256$\times$256에서의 비교 결과이다.

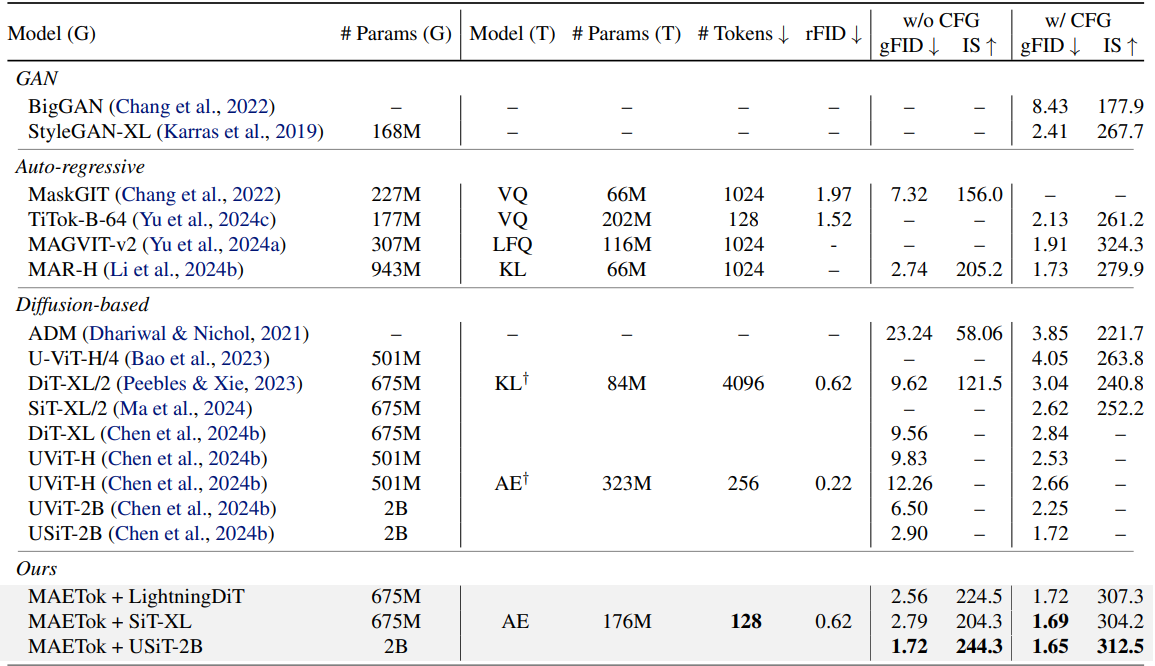
다음은 ImageNet 512$\times$512에서의 비교 결과이다.

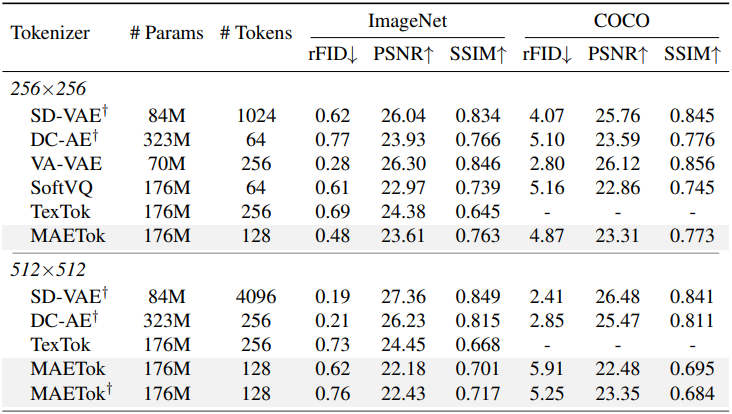
다음은 다양한 continuous tokenizer와의 비교 결과이다.

4. Discussion

다음은 unconditional generation 성능을 비교한 결과이다.

다음은 MAETok의 구성 요소에 대한 효과를 비교한 결과이다.