[논문리뷰] Competition and Attraction Improve Model Fusion

GECCO 2025. [Paper] [Github]
João Abrantes, Robert Tjarko Lange, Yujin Tang
Sakana AI
22 Aug 2025

Introduction

모델 병합(model merging)은 처음에는 시드 모델을 결합하기 위해 계수를 수동으로 조정하는 방식에 의존했다. 이 과정은 직관에 기반했으며, 특정 task의 성능을 최적화하기 위해 상당한 시행착오를 거쳐야 했다. 최근 진화 알고리즘은 최적의 계수를 자동으로 검색하여 이 과정을 간소화하여 병합 효율성을 크게 향상시켰다. 그러나 병합 전에 모델 파라미터를 고정된 집합으로 그룹화해야 하므로 잠재적인 조합에 대한 검색 공간이 제한된다. 이러한 한계를 해결하기 위해, 본 논문에서는 세 가지 주요 특징을 가진 진화 알고리즘인 Model Merging of Natural Niches (M2N2)를 제안하였다.

병합 경계의 진화

기존 방법은 각 시드 모델의 파라미터를 고정된 그룹(ex. 레이어)으로 분할하고 이러한 미리 정의된 경계 내에서 병합 계수를 최적화하여 탐색 범위를 제한하였다. 반면, M2N2는 유연한 분할점을 사용하여 파라미터를 분할하는 방식으로 두 모델을 한 번에 반복적으로 병합한다. 정적인 모델을 사용하는 대신, 진화하는 모델 아카이브를 유지한다. Generation 수가 증가함에 따라 M2N2는 더 광범위한 경계와 계수를 점진적으로 탐색하여 필요한 경우 점점 더 복잡한 조합을 가능하게 한다. 이처럼 점진적이고 선택적으로 복잡성을 증가시키면 계산 효율성을 유지하면서 더 광범위한 탐색이 가능하다.

다양성 관리

모델 병합에서 다양성 보존이 필수적이다. 그러나 어떤 특성을 다양성으로 유지해야 하는지 정의하는 것이 어렵다. 많은 방법들은 수동으로 지정된 다양성 metric을 필요로 하지만, 모델과 task의 복잡성이 증가함에 따라 효율적인 다양성 metric을 도출하는 것이 점점 더 어려워지고 있다. 대신, 제한된 자원에 대한 경쟁을 통해 고성능 모델의 다양성을 장려한다.

Attraction

본 논문에서는 모델의 상호 보완적인 강점을 기반으로 모델을 페어링하는 휴리스틱을 도입하여 효율성과 최종 모델 성능을 모두 향상시켰다. Mate selection은 유전 알고리즘에서 아직 충분히 연구되지 않은 영역이지만, 병합의 계산 비용이 증가함에 따라 점점 더 중요해지고 있다. M2N2는 이 요소의 중요성을 강조하고 이 분야의 추가 연구를 장려한다.

Method

모델 병합(model merging)의 목표는 모델 파라미터가 각각 \(\theta_i\)인 $K$개의 시드 모델 집합에서 병합된 모델에 대한 최적 파라미터 $\theta^\ast$를 찾는 것이다. 이를 통해 일반적으로 task 점수의 합이나 평균 형태로 나타나는 최적화 목표가 최대화된다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \max} \sum_{j=1}^N s (x_j \, \vert \, \theta) \\ \textrm{where} \; \theta = h_w (\theta_1, \ldots, \theta_K) \end{equation}\]

($h_w$는 모델 병합 함수, $s$는 특정 task의 score function, $x_j$는 task 예제, $N$은 예제 수)

M2N2에서는 병합 경계의 진화를 허용하기 위해 병합 함수 $h$에 대한 수정과 다양성을 촉진하기 위한 최적화 목표에 대한 조정을 제안하였다.

1. Eliminating Fixed Model Merging Boundaries

위 식에서 $\theta^\ast$를 찾는 것은 $h_w$에서 최적의 모델 병합 파라미터 $w$를 찾는 것으로 귀결된다. 저자들은 고정된 모델 병합 경계의 제약을 없애고 더 큰 유연성을 허용하기 위해, 이러한 경계를 혼합 파라미터와 함께 진화 과정에 포함시켰다.

구체적으로, M2N2는 $K$개의 시드 모델로 초기화된 모델 아카이브를 유지한다. 각 학습 단계에서 M2N2는 아카이브에서 두 모델 $A$와 $B$를 무작위로 선택하고, 모델 파라미터 공간에서 혼합 비율과 분할점을 결정하는 두 파라미터 $(w_m, w_s)$를 샘플링한다. 그런 다음, 다음 식을 사용하여 모델 $A$와 $B$를 병합하고, 아카이브에서 성능이 가장 나쁜 모델보다 새로 병합한 모델의 성능이 우수한 경우 새 모델을 아카이브에 삽입한다.

\[\begin{equation} h_\textrm{M2N2} (\theta_A, \theta_B, w_m, w_s) = \textrm{concat} (f_{w_m} (\theta_A^{< w_s}, \theta_B^{< w_s}), f_{1 - w_m} (\theta_A^{\ge w_s}, \theta_B^{\ge w_s})) \end{equation}\]

\(\theta^{< w_s}\)와 \(\theta^{\ge w_s}\)는 $w_s$를 기준으로 모델 파라미터를 분할한 것이고, \(f_t (\theta_A, \theta_B)\)는 \(\theta_A\)와 \(\theta_B\)를 $t$로 interpolation하는 SLERP 함수이다. 본 방법은 더 넓은 경계와 계수를 탐색하여 탐색 공간을 점진적으로 확장한다. 이러한 점진적인 복잡성 도입은 계산 용이성을 유지하면서도 더 넓은 범위의 가능성을 보장한다.

2. Encouraging Diversity via a Modified Optimization Goal

제한된 자원을 놓고 경쟁하는 것은 자연스럽게 다양성을 증진시켜, 경쟁이 덜한 자원을 활용할 수 있는 개인에게 유리하게 작용한다. 모든 예제의 점수 합이 최대화되는 최적화 목표의 맥락에서, 각 점수는 솔루션의 적합도에 기여하는 “자원”이다. 자원 공급을 제한함으로써 M2N2는 경쟁을 촉발하고, 이는 자연스럽게 새로운 틈새 시장을 차지하는 개인에게 유리하게 작용한다.

구체적으로, 모집단이 데이터 포인트 $x_j$에서 추출할 수 있는 총 적합도를 용량 $c_j$로 제한한다. 후보 솔루션이 데이터 포인트에서 도출하는 적합도의 양은 모집단의 총 점수에 대한 해당 점수에 비례한다. 수정된 최적화 목표는 다음과 같다.

\[\begin{equation} \theta^\ast = \underset{\theta}{\arg \max} \sum_{j=1}^N \frac{s (x_j \, \vert \, \theta)}{z_j + \epsilon} c_j \\ \textrm{where} \; z_j = \sum_{k=1}^P s (x_j \, \vert \, \theta_k) \end{equation}\]

($\epsilon$은 0으로 나눠지는 것을 방지하기 위한 작은 숫자, $P$는 아카이브 크기)

용량 $c_j$는 task에 따라 달라지며 여러 가지 방법으로 정의할 수 있다. 예를 들어, binary scoring task (즉, \(s(\cdot) \in \{0, 1\}\))에서는 간단히 $c_j = 1$로 설정한다. Reward가 0에서 1까지 continuous한 경우에는 \(c_j = \max_i s(x_j \vert \theta_i)\)로 정의하여 부분적으로 해결된 데이터 포인트(\(\max_i s(x_j \vert \theta_i) < 1\))가 완전히 해결된 데이터 포인트(\(\max_i s(x_j \vert \theta_i) = 1\))와 동일한 양으로 분배하지 않도록 한다.

3. Sampling Parents via Attraction

많은 진화 알고리즘은 두 부모의 장점을 결합하기 위해 crossover 연산을 사용한다. 모델 병합과 같은 더 비용이 많이 드는 crossover 연산을 사용함에 따라 배우자 선택 알고리즘의 중요성이 점점 더 커진다.

아카이브에서 성능이 가장 좋은 모델에 더 많은 샘플링 확률을 부여하는 기존 방식과 달리, M2N2는 부모 모델의 상보성을 고려하는 추가적인 고려 사항을 추가하였다. 구체적으로, 앞서 정의한 점수의 가중 합을 기반으로 첫 번째 부모 모델을 샘플링한 다음, 첫 번째 부모에 맞게 특별히 조정된 함수 $g$로 생성된 attraction score를 기반으로 두 번째 부모 모델을 샘플링한다. 아래 식은 attraction score의 정의이며, 모델 $A$의 성능이 떨어지는 데이터 포인트에서 성능이 좋은 모델 $B$를 선택하려는 욕구를 명확하게 표현하면서, 용량 $c_j$가 높고 경쟁 $z_j$가 낮은 리소스에 더 많은 우선권을 부여한다.

\[\begin{equation} g(\theta_A, \theta_B) = \sum_{j=1}^N \frac{c_j}{z_j + \epsilon} \max (s(x_j \, \vert \, \theta_B) - s(x_j \, \vert \, \theta_A), 0) \end{equation}\]

Experiments

1. Evolving MNIST classifier

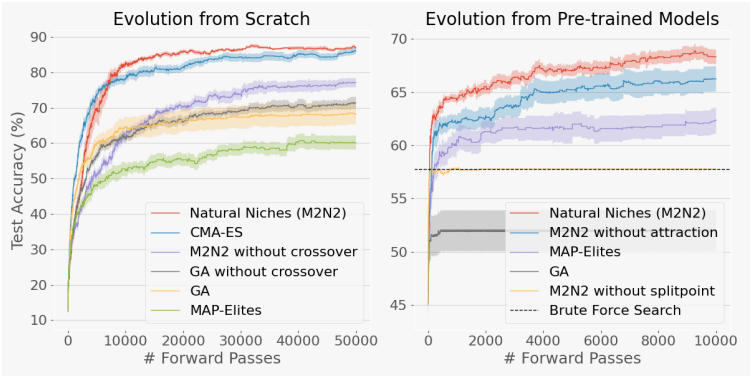
다음은 파라미터가 19,210개인 2-layer classifier에 대한 MNIST 실험 결과이다.

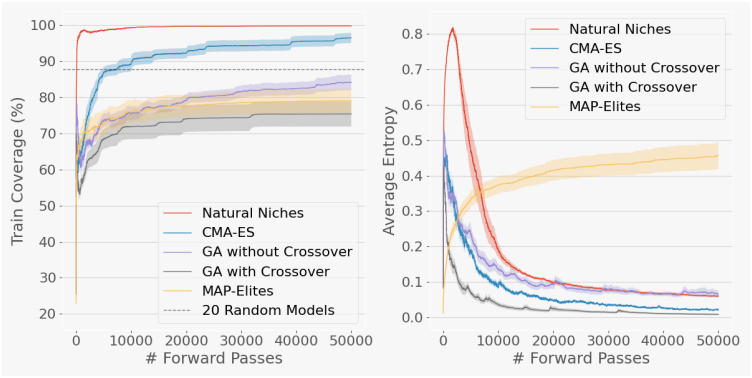
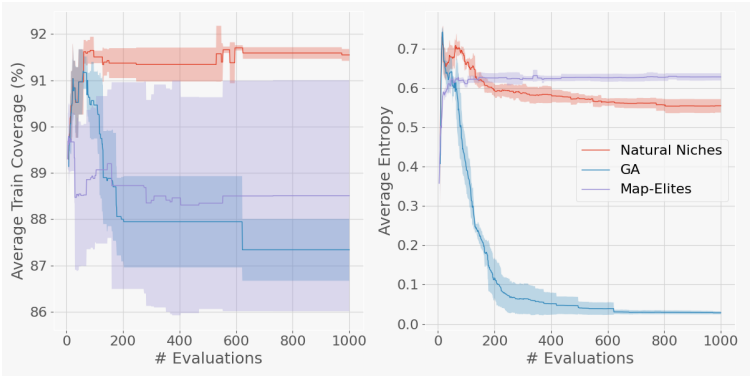
다음은 처음부터 진화시킨 classifier에 대한 다양성을 분석한 결과이다. 왼쪽 그래프는 아카이브에서 적어도 하나의 모델이 올바르게 레이블링될 수 있는 학습 데이터 포인트의 비율이다. 오른쪽 그래프는 학습 과정에서 아카이브 내의 모델에 대한 성능의 다양성을 엔트로피로 측정한 것이다.

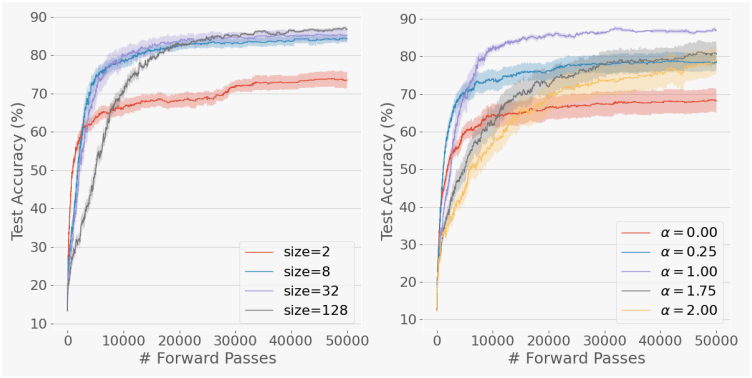
다음은 (왼쪽) 아카이브 크기 $P$에 따른 성능과 (오른쪽) $P = 20$일 때 아래 식에서 $\alpha$ 값에 따른 성능을 비교한 그래프이다.

\[\begin{equation} f(\theta_i) = \sum_{j=1}^N \frac{s (x_j \, \vert \, \theta_i)}{z_j^\alpha + \epsilon} c_j \end{equation}\]

2. Combining LLMs with Math and Agentic Skills

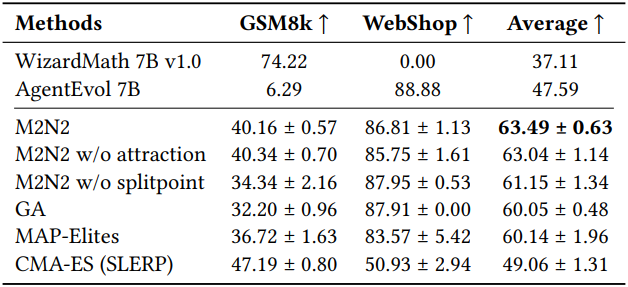
다음은 수학 전문 모델인 WizardMath-7B-V1.0과 에이전트 환경에 대한 전문 모델인 AgentEvol-7B를 병합한 다음, 수학 벤치마크인 GSM8k와 웹쇼핑 벤치마크인 WebShop에서의 성능을 측정한 결과이다.

다음은 MNIST classifier와 마찬가지로 병합된 LLM의 다양성을 분석한 결과이다.

3. Merging Diffusion-Based Image Generation Models

다음은 4개의 이미지 생성 모델을 병합한 결과이다. 구체적으로 일본어 프롬프트로 학습된 JSDXL과 영어 프롬프트로 학습된 SDXL 1.0, SDXL-PRO, Juggernaut-XL-v9을 병합하였다.

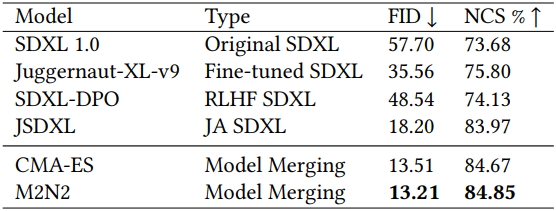
다음은 COCO 캡션에 대한 각 시드 모델과 병합된 모델의 생성 결과를 비교한 것이다.

다음은 일본어 프롬프트와 영어 프롬프트에 대한 각 시드 모델과 병합된 모델의 생성 결과를 비교한 것이다.

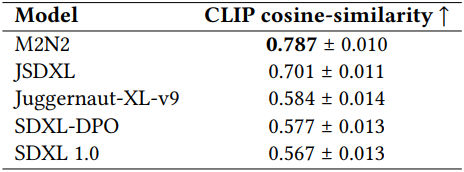
다음은 일본어 프롬프트와 영어 프롬프트로 각각 생성한 결과 사이의 CLIP feature 유사도를 비교한 표이다.

Limitations

모델 병합의 실현 가능성은 모델 간의 유사성 정도에 따라 크게 달라진다. Fine-tuning된 모델이 base model과 크게 다를 경우 병합에 실패하게 된다. 저자들은 분산된 state 표현을 가진 모델이 병합에 적합하지 않다는 가설을 세웠지만, 모델 호환성을 평가하는 표준화된 지표는 아직 확립되지 않았다.