[논문리뷰] LumiGauss: Relightable Gaussian Splatting in the Wild

WACV 2025. [Paper] [Github]
Joanna Kaleta, Kacper Kania, Tomasz Trzcinski, Marek Kowalski
Warsaw University of Technology | Sano Centre for Computational Medicine | Microsoft | IDEAS NCBR | Tooploox
6 Aug 2024

Introduction

본 논문에서는 야외에서 촬영한 이미지에 inverse graphics를 수행하기 위해 2DGS를 사용하는 방법인 LumiGauss를 제안하였다. 이전 방법들과 달리, LumiGauss는 고품질 렌더링을 유지하고 그래픽 엔진과 쉽게 통합할 수 있는 동시에 빠른 학습 및 inference 속도가 특징이다.

LumiGauss에서 빛은 environment map과 주어진 surfel을 비추는 environment map의 부분을 나타내는 radiance transfer function의 조합으로 모델링되며, 둘 다 spherical harmonics (SH)로 모델링된다. 이 접근 방식은 그림자를 모델링할 수 있지만 다른 물체에서 반사된 빛을 표현할 가능성도 있다.

LumiGauss의 출력은 학습 중에 사용할 수 있는 것 이상의 environment map을 사용하여 novel view synthesis와 relighting을 모두 가능하게 한다. 미리 계산된 radiance transfer가 제공하는 가능성을 활용하여 LumiGauss의 표현은 게임 엔진에 완벽하게 통합되어 빠르고 효율적인 relighting을 가능하게 한다.

Method

1. Preliminaries on Radiance Transfer

단순화된 형태의 렌더링 방정식은 벡터 \(\omega_o\)를 따라 점 $x$에서 나오는 빛 \(L(x, \omega_o)\)를 나타내는 적분 함수이다.

\[\begin{equation} L(x, \omega_o) = \int_s f_r (x, \omega_o, \omega_i) L_i (x, \omega_i) D (x, \omega_i) d \omega_i \end{equation}\]

($f_r (\cdot)$은 BRDF 함수, $L_i (x, \omega_i)$는 $\omega_i$에서 $x$로 들어오는 빛, $D(\cdot)$는 radiance transfer function)

직관적으로, $f_r (\cdot)$은 표면 재료를 나타내고, $L_i (x, \omega_i)$는 조명의 강도와 색상을 나타내며, $D(\cdot)$는 그림자 또는 다른 표면에서 오는 빛 반사를 고려하는 항이다. 이러한 함수들에 따라 렌더링 방정식은 간단하고 부정확한 조명 모델에서 매우 복잡하고 정확한 모델까지 다양할 수 있다.

Unshadowed model

위 렌더링 방정식으로 표현할 수 있는 반사 모델의 한 예는 난반사 모델로, dot product lighting이라고도 한다. Diffuse BRDF는 빛을 균일하게 반사하여 lighting을 뷰에 독립적으로 만들고 BRDF를 다음과 같이 단순화한다.

\[\begin{equation} L_D (x) = \frac{\rho (x)}{\pi} \int_s L_i (x, \omega_i) \max (n(x) \cdot \omega_i, 0) d \omega_i \end{equation}\]

($\rho$는 albedo, $n(x)$는 $x$에서의 normal)

들어오는 빛 \(L_i (x, \omega_i)\)는 여러 가지 방법으로 표현할 수 있다. 본 논문에서는 omnidirectional environment map으로 조명된다고 가정하였으며, 이 environment map은 $(n+1)^2$개의 계수를 가진 degree $n$의 spherical harmonics (SH)를 사용하여 parametrize된다. Environment map이 장면에서 무한히 멀리 떨어져 있기 때문에 빛은 위치에 독립적이며 따라서 렌더링 방정식이 더욱 단순화된다.

\[\begin{equation} L_U (x) = \frac{\rho (x)}{\pi} \int_s L_i (\omega_i) \max (n(x) \cdot \omega_i, 0) d \omega_i \end{equation}\]

SH로 parametrize된 조명을 사용하면 closed-form solution으로 적분을 계산할 수 있다.

Shadowed model

저자들은 unshadowed model 외에도 \(D(x, \omega_i)\)가 SH를 사용하여 parametrize되고 학습 데이터에서 학습되는 shadowed model을 제안하였다. \(D(x, \omega_i)\)에서 SH는 environment map의 각 방향에서 공간의 연관된 지점으로 도착하는 빛을 정량화하는 구면 신호를 나타낸다. Shadowed model은 다음과 같다.

\[\begin{equation} L_S (x) = \frac{\rho (x)}{\pi} \int_s L_i (\omega_i) D (x, \omega_i) d \omega_i \end{equation}\]

이 접근법은 그림자를 모델링하는 것 외에도, 장면 내 물체 사이의 빛의 inter-reflection을 모델링할 수 있는 잠재력을 가지고 있다.

Environment map과 radiance transfer function에 동일한 degree의 SH를 사용하면 위의 렌더링 방정식을 효율적으로 계산할 수 있다. SH는 직교성 덕분에 두 SH 기반 함수의 적분을 계수의 내적으로 단순화할 수 있다.

\[\begin{equation} L_S (x) = \frac{\rho (x)}{\pi} l \cdot d \end{equation}\]

($l \in \mathbb{R}^{(n+1)^2}$은 \(L_i (\omega_i)\)의 SH 계수, $d \in \mathbb{R}^{(n+1)^2}$은 \(D (x, \omega_i)\)의 SH 계수)

2. LumiGauss

LumiGauss는 야외에서 촬영한 $c \le C$개의 이미지 \(\{\mathcal{I}_c\}_{c=1}^C\)과 연관된 카메라 \(\{\mathcal{C}_c\}_{c=1}^C\)서 2D Gaussian을 사용하여 relighting 가능한 모델의 3D 표현을 생성한다. 본 논문의 목표는 rasterization 후 해당 이미지를 재생성하는 Gaussian 파라미터

\[\begin{equation} \mathcal{G} = \{t_k, R_k, s_k, o_k, \rho_k, d_k\}_{k=1}^K \end{equation}\]

를 찾는 것이다. 다음과 같은 목적 함수를 최소화하여 Gaussian을 최적화한다.

\[\begin{equation} \underset{\mathcal{G}, \mathcal{E}, \theta}{\arg \min} \mathbb{E}_{\mathcal{C}_c \sim \{\mathcal{C}_c\}} \ell_\textrm{rgb} (\mathcal{S} (\mathcal{C}_c \, \vert \, \mathcal{G}, \mathcal{E}, \theta), \mathcal{I}_c) + \mathcal{R} (\mathcal{G}) \end{equation}\]

(\(\mathcal{E} = \{e_c\}_{c=1}^C\))는 학습 가능한 environment embedding, \(\ell_\textrm{rgb}\)은 reconstruction loss, $\mathcal{S}$는 렌더링 함수, $\mathcal{R}$은 정규화 항)

2DGS와 대조적으로 각 Gaussian에 대해 기본 색상 $\rho$를 diffuse로 모델링하고 radiance transfer function $d$에 대해 SH 계수를 도입한다. 2DGS는 relighting을 가능하게 하는 부드러운 normal을 제공한다.

Relighting

야외 이미지의 다양한 조명 조건을 처리하기 위해 각 학습 이미지를 조명 조건을 인코딩하는 학습 가능한 latent code $e_c$와 연관시킨다. 이 임베딩을 사용하여 MLP를 통해 environment map 계수를 예측한다.

\[\begin{equation} l_c = \textrm{MLP} (e_c \vert \theta) \end{equation}\]

예측된 조명은 렌더링 프로세스에서 두 가지 방식, 즉 unshadowed와 shadowed 중 하나로 사용된다.

Unshadowed model

그림자가 없는 시나리오의 경우, 우리는 표면 normal 방향으로 반구에 걸쳐 빛을 적분한다. Normal $n_k$와 조명 파라미터 $l_c$가 주어진 각 Gaussian $G_k$에 대한 색상 $c_k$는 다음과 같다.

\[\begin{equation} c_k = \rho_k \odot \underbrace{n_k^\top M(l_k) n_k}_{\textrm{unshadowed irradiance}} \end{equation}\]

($M$은 environment map의 SH 파라미터에서 파생된 $4 \times 4$ 행렬)

이 간단하면서도 효과적인 모델은 이미 모델에 relighting 기능을 부여한다. 그러나 그림자를 올바르게 포착하지 못해 출력의 충실도가 제한된다.

Shadowed model

모델에서 그림자를 효과적으로 포착하기 위해 Gaussian의 출력 색상을 \(\tilde{c}_k\) c˜k로 재정의한다.

\[\begin{equation} \tilde{c}_k = \rho_k \odot \underbrace{\sum_{i=1}^{(n+1)^2} l_c^i \cdot d_k^i}_{\textrm{shadowed irradiance}} \end{equation}\]

그림자를 추가하면 더 정확한 relighting이 가능하다. 또한 inference 단계에서 그림자를 재구성하는 데 MLP가 필요하지 않아 렌더링 엔진에 직접 적용할 수 있다는 장점이 있다.

3. Physical constraints

2DGS에서 제안된 정규화는 Gaussian을 표면에 가깝게 유지하고 국소적으로 매끄럽게 만드는데, 이는 relighting 시나리오에서 매우 중요하다. 저자들은 이 외에도 물리적 빛 속성에 기반한 새로운 loss 항을 제안하였다.

Radiance transfer function $D_k$를 [0, 1] 범위 내로 제한한다. 여기서 0은 완전한 그림자를 나타내고 1은 조명에 완전히 노출된 것을 나타낸다.

\[\begin{equation} \ell_{0-1} = \mathbb{E}_k \mathbb{E}_{\omega_i} [\| \max (D_k (\omega_i), 1) - 1 \|_2^2 + \| \min (D_k (\omega_i), 0) \|_2^2] \end{equation}\]

또한 environment map이 항상 양의 값을 가지도록 제한한다.

\[\begin{equation} \ell_{+} = \mathbb{E}_k \mathbb{E}_{\omega_i} \| \min (L_c (\omega_i), 0) \|_2^2 \end{equation}\]

Shadowed radiance transfer는 unshadowed radiance transfer와 가깝게 유지되어야 한다. 그렇지 않으면 shadowed radiance transfer에 모든 방향의 빛이 포함되어 잘못된 relighting이 발생할 수 있다.

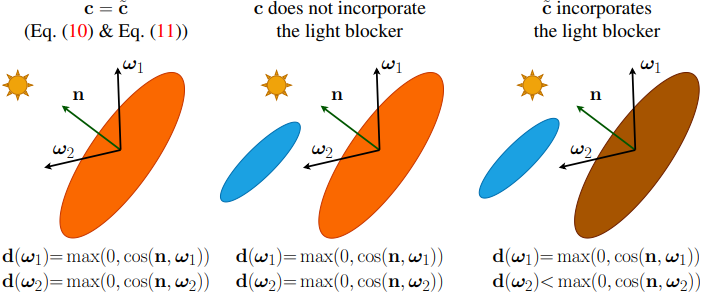
이 문제를 해결하기 위해 다음과 같은 loss function을 추가한다.

\[\begin{equation} \ell_{◐ \leftrightarrow ⭘} = \mathbb{E}_k \mathbb{E}_{\omega_i} \| \max (n_k \cdot \omega_i, 0) - D_k (\omega_i) \|_2^2 \end{equation}\]

적용된 transfer function은 본질적으로 그림자와 inter-reflection을 고려한다. 그림자 모델링에 특히 집중하고 shadowed radiance의 사용을 제한하기 위해 shadowed radiance가 unshadowed radiance보다 밝지 않도록 보장하는 loss function을 추가한다.

\[\begin{equation} \ell_{◐} = \mathbb{E}_k \mathbb{E}_{\omega_i} \| \max (D_k (\omega_i) - \max (n_k \cdot \omega_i, 0), 0) \|_2^2 \end{equation}\]

전체 정규화 항은 다음과 같다.

\[\begin{equation} \mathcal{R} (\mathcal{G}) = \lambda_1 \ell_{1-0} + \lambda_2 \ell_{+} + \lambda_3 \ell_{◐ \leftrightarrow ⭘} + \lambda_4 \ell_{◐} \end{equation}\]

4. Reconstruction

2DGS에서 제안된 splatting 알고리즘 $\mathcal{S}(\cdot)$을 사용하여 이미지를 렌더링한 후, 렌더링된 이미지를 ground-truth \(\{\mathcal{I}_c\}\)와 비교한다. Reconstruction loss \(\ell_\textrm{rgb}\)는 다음과 같다.

\[\begin{equation} \ell_\textrm{rgb} = \lambda_\textrm{rec} (◐) \ell_\textrm{rec} (⭘) + \lambda_\textrm{rec} (◐) \ell_\textrm{rec} (⭘) \\ \textrm{where} \; \ell_\textrm{rec} (\{◐,⭘\}) = \ell_1 (\{◐,⭘\}) + \lambda \ell_\textrm{D-SSIM} (\{◐,⭘\}) \end{equation}\]

($\lambda = 0.2$)

더 복잡한 shadowed model을 처음부터 학습시키면 local minima에 도달하므로, \(\lambda_\textrm{rec} (◐) = 0.0\)와 \(\lambda_\textrm{rec} (⭘) = 1.0\)으로 학습을 시작하여 unshadowed model만 학습시킨다. Unshadowed model이 수렴하면, \(\lambda_\textrm{rec} (◐) = 1.0\)으로 \(\lambda_\textrm{rec} (⭘)\)를 작은 값으로 전환하여 shadowed model이 unshadowed model로 설명할 수 없는 이미지의 그림자 부분을 설명하도록 한다.

Experiments

• 데이터셋: Shiny Blender, Glossy Synthetic, Ref-Real

1. Scene reconstruction and relightning

다음은 장면 재구성 및 relighting 예시들이다.

다음은 LumiGauss와 다른 방법들의 albedo, normal, relighting을 비교한 결과이다.

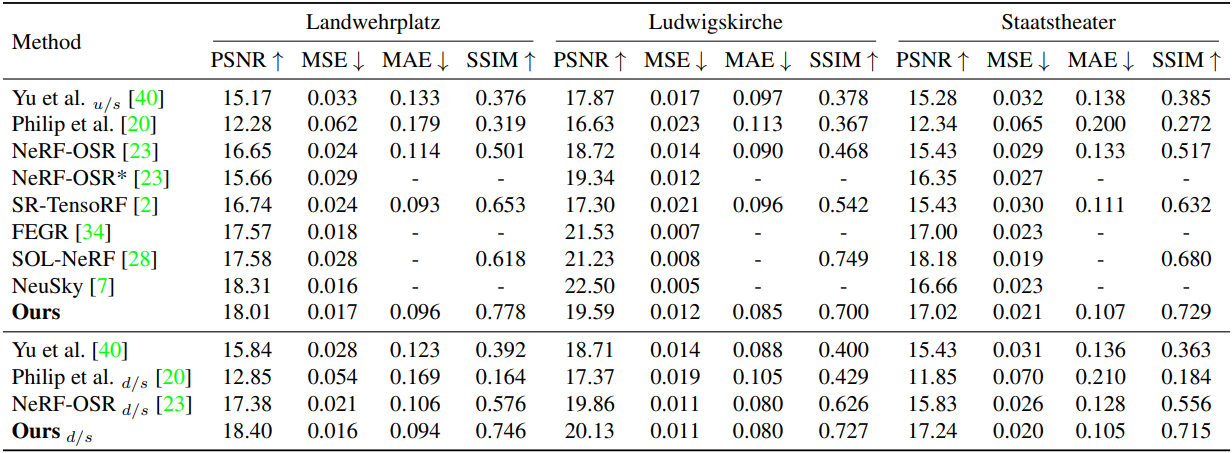
다음은 LumiGauss와 다른 방법들의 렌더링 품질을 비교한 결과이다. (u/s와 d/s는 각각 업샘플링, 다운샘플링)

다음은 environment map에 따른 shadowed model과 unshadowed model의 렌더링을 비교한 것이다. 그림자는 두 렌더링 결과의 차이로 계산되었다.

2. Ablations

다음은 ablation 결과이다. $\dagger$는 두 번째 학습 단계에서 \(\ell_{◐ \leftrightarrow ⭘}\)와 \(\ell_\textrm{rec} (⭘)\)를 생략한 경우이며, $\ddagger$는 첫 번째 학습 단계를 생략한 경우이다.

다음은 그림자 학습에 대한 ablation 결과를 시각화한 것이다.

3. Performance comparison

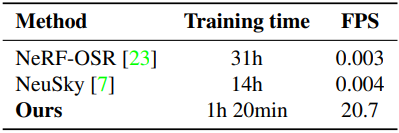
다음은 학습 시간과 inference 속도를 비교한 표이다.

Limitations

1. 뚜렷하고 빈번한 그림자가 있는 시나리오에서 albedo와 normal이 그림자를 시뮬레이션하려고 할 수 있다. 이는 그림자 학습에 어려움을 줄 수 있으며, 특히 여러 학습 이미지에서 그림자가 보일 때 normal의 정확한 표현을 방해할 수 있다.
2. 그림자는 창문과 같은 반사 표면에 부자연스럽게 나타날 수 있다.
3. SH 표현에 내장된 그림자 모델링을 자율 주행과 같은 동적 애플리케이션으로 확장하는 것이 간단하지 않다.