[논문리뷰] Latent Radiance Fields with 3D-aware 2D Representations
ICLR 2025. [Paper] [Page] [Github]
Chaoyi Zhou, Xi Liu, Feng Luo, Siyu Huang
Clemson University
13 Feb 2025

Introduction
2D latent space와 3D 표현 사이의 간극을 메우는 데에는 두 가지 주요 과제가 있다.
- 2D latent space에 존재하는 시점에 따라 다른 고주파 노이즈가 기하학적 일관성 부족과 불안정한 최적화를 초래한다.
- Latent feature에 RGB 기반 novel view synthesis (NVS) 방법을 적용함에 따라 발생하는 데이터 분포 변화는 사실적인 렌더링을 저해한다.
이러한 두 가지 문제를 해결하기 위해, 저자들은 오토인코더의 표현 능력을 최대한 보존하면서 3D 인식 능력을 latent space에 내장하고자 하였다. 또한 이러한 2D 표현을 기반으로 latent radiance field (LRF)을 구축하는 새로운 프레임워크를 제안하였다. 구체적으로, 이 프레임워크는 세 단계로 구성된다.
- VAE의 latent space에 대한 3D 인식을 향상시켜 2D 표현이 기하학적 일관성을 유지하도록 하는 correspondence 기반 오토인코딩 방법을 도입하였다.
- 3D 인식 능력이 생긴 2D 표현으로부터 3D 장면을 표현하는 LRF를 구축하여, 2D 표현을 3D 공간으로 확장하였다.
- NVS로 인한 데이터 분포 변화를 더욱 완화하고 렌더링된 2D 표현으로부터의 이미지 디코딩 성능을 향상시키기 위해 VAE-Radiance Field(VAE-RF) 정렬 방법을 도입하였다.
이렇게 생성된 3D-aware latent space와 LRF는 추가적인 fine-tuning 없이 기존 NVS 또는 3D 생성 파이프라인에 원활하게 통합되어 고품질의 사실적인 합성 결과를 얻을 수 있다.
Method
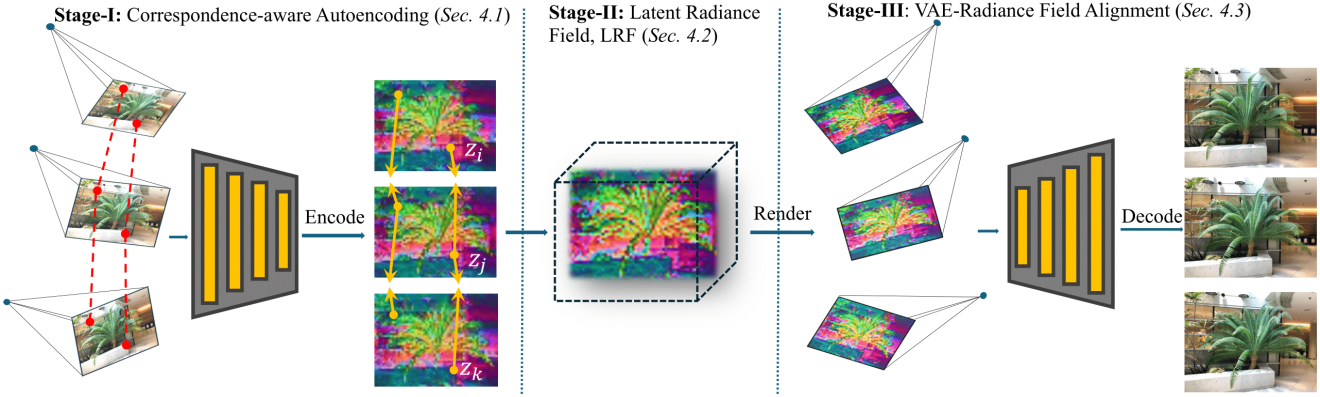
1. Correspondece-aware Autoencoding
첫 번째 단계는 기하학적 정보를 오토인코딩 과정에 통합하는 것이다. $K$개의 멀티뷰 이미지 \(\mathcal{I} = \{\textbf{I}_i\}_{i=1}^K, (\textbf{I}_i \in \mathbb{R}^{H \times W \times 3})\)가 주어졌을 때, VAE 인코더는 semantic 정보를 효과적으로 보존하면서 저차원 latent space에서 2D 표현 \(\mathcal{Z} = \{\textbf{Z}_i\}_{i=1}^K, (\textbf{Z}_i \in \mathbb{R}^{H^\prime \times W^\prime \times 4})\)를 추출한다.
그러나 기존의 대부분의 NVS 프레임워크는 렌더링된 latent space에서 사실적인 이미지를 재구성하는 데 실패하였다. 이는 주로 VAE 인코딩 과정에서 원본 이미지 공간 내의 멀티뷰 일관성이 크게 손상되기 때문이다. Latent space는 원본 RGB 공간을 압축된 latent space로 만들기 위해 대량의 고주파 노이즈를 포함하고 있다. 이로 인해 3D 공간에서 2D latent 표현을 재구성하는 데 심각한 어려움이 발생한다.
위의 문제를 해결하고 효과적인 latent 3D 재구성을 위해, 저자들은 멀티뷰 correspondence 일관성에서 영감을 얻었다. 구체적으로, 이미지 \(\textbf{I}_i\)의 점 $\textbf{x}i \in \mathbb{R}^2\(와 다른 이미지\)\textbf{I}_j\(의 점\)\textbf{x}_j \in \mathbb{R}^2\(는 fundamental matrix\)\textbf{F}{ij} \in \mathbb{R}^{3 \times 3}$$로 연결되어 다음과 같은 멀티뷰 제약 조건을 만족하는 경우 correspondence로 간주된다.
\[\begin{equation} \textbf{x}_j^\top \textbf{F}_{ij} \textbf{x}_i = 0 \end{equation}\]이 식은 이미지 공간 상의 correspondence 쌍이 서로 가까워야 3D 공간 최적화 과정에서 일관된 geometry를 보장할 수 있음을 나타낸다. 그렇지 않으면, local minima로 인한 아티팩트와 중복된 기하학적 표현이 3D 재구성 및 NVS의 품질을 저하시킬 수 있다.
이러한 점에 착안하여, 본 논문에서는 correspondence 일관성을 오토인코더 학습에 통합하는 계산 효율적인 전략을 제안하였다. 구체적으로, \(\mathcal{I} = \{\textbf{I}_i\}_{i=1}^K\)를 오토인코더에 입력하여 latent 표현 \(\mathcal{Z} = \{\textbf{Z}_i\}_{i=1}^K\)를 추출하고, latent space에서의 correspondence 일관성 loss를 다음과 같이 계산한다.
\[\begin{equation} \mathcal{L}_\textrm{corres} = \sum_{i=1}^K \sum_{j \in \mathcal{K} (i)} \lambda_{ij} \| \textbf{z}_i - \textbf{z}_j \|_1 \end{equation}\]\(\mathcal{L}_\textrm{corres}\)는 인코딩된 feature가 멀티뷰 이미지에서 파생된 correspondence 일관성을 따르도록 보장한다. \(\lambda_{ij}\)는 average pose error (APE)를 기반으로 하는 가중치로, APE는 이미지 \(\textbf{I}_i\)와 \(\textbf{I}_j\)의 카메라 포즈 사이의 Frobenius norm으로 계산된다.
VAE 학습 loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{StageI} = \mathcal{L}_\textrm{VAE} + \lambda_1 \mathcal{L}_\textrm{corres} + \lambda_2 \mathcal{L}_\textrm{reg} \end{equation}\]NVS 방법에서는 시점 의존적 정보를 효율적이고 robust하게 모델링하기 위해 spherical harmonics (SH)의 최대 degree를 항상 3으로 설정한다. 낮은 degree의 항은 장면의 albedo와 같은 저주파 정보를 주로 포착하는 데 사용되는 반면, 높은 degree의 항은 조명과 같은 고주파 시점 의존적 정보를 모델링하는 데 사용된다.
Latent space의 경우, latent code는 기본값과 고주파 노이즈의 조합으로 간주할 수 있다. 이러한 압축된 표현 방식 때문에 노이즈 양이 RGB 공간에 비해 크게 증가할 수 있으며, 이로 인해 SH 함수 계수가 다양한 시점의 정보를 모델링하는 데 어려움이 발생한다. 최대 degree가 고정되면 SH 함수 계수가 글로벌 최적값에 도달하기가 더 쉬워진다.

다행히 본 논문에서 제안하는 Lcorres는 고품질 이미지 생성 능력을 유지하면서 고주파 노이즈를 효과적으로 제거할 수 있어 최적화 과정이 더욱 안정적이고 기하학적 표현이 일관적이다. 위 그림은 correspondence-aware 인코딩이 2D latent space의 고주파 노이즈를 효과적으로 제거할 수 있음을 보여준다. 또한 FFT를 적용한 시각화 결과에서도 latent space에서 고주파 노이즈가 감소된 것을 확인할 수 있으며, 이는 2D feature를 3D latent field로 추출하는 데 효과적인 접근 방식임을 시사한다.
2. Latent Radiance Field
3D-aware한 2D 표현 fine-tuning을 기반으로, VAE의 2D latent space, 즉 latent radiance field (LRF)에 3D 표현을 직접 생성한다. 본 논문에서는 radiance field 표현의 예로 3DGS를 사용하였다.
3DGS와 마찬가지로 latent 3D Gaussian은 다음과 같이 구성된다.
\[\begin{equation} \mathcal{G} = \{(\boldsymbol{\mu}, \textbf{s}, \textbf{R}, \alpha, \textbf{SH}_f)_j\}_{1 \le j \le M} \end{equation}\]3DGS의 미분 가능한 rasterization 과정을 따라, 포인트 기반 알파 블렌딩을 사용하여 2D latent 표현을 rasterization한다.
\[\begin{equation} \textbf{Z} = \sum_{i \in \mathcal{N}} \textbf{z}_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_i) \end{equation}\]Rasterization 함수 $r$은 카메라 포즈 \(\textbf{P}_i\)에 따라 latent Gaussian 집합을 2D latent 표현으로 렌더링한다. 그런 다음 latent Gaussian 파라미터를 최적화하여 latent $\mathcal{Z}$를 최적으로 표현한다.
\[\begin{equation} \hat{\mathcal{G}} = \underset{\{(\boldsymbol{\mu}, \textbf{s}, \textbf{R}, \alpha, \textbf{SH}_f)\}}{\arg \min} \sum_{i=1}^N \mathcal{L}^f (r (\mathcal{G}, \textbf{P}_i), \textbf{Z}_i) \end{equation}\](\(\mathcal{L}^f\)는 \(\ell_1\) loss와 D-SSIM loss의 결합)
Correspondece-aware autoencoder는 3D 공간에서 기하학적으로 일관된 2D 표현을 보장하기 때문에 추가적인 geometry 일관성 제약 조건을 적용할 필요가 없다. 따라서 LRF는 2D latent 표현을 radiance field 표현으로 직접 재구성하여 새로운 시점에 대한 2D latent 표현의 효율적인 렌더링을 가능하게 한다.
3. VAE-Radiance Field Alignment
Correspondece-aware autoencoding은 VAE latent space의 3D 일관성을 향상시키지만, 뉴럴 렌더링의 비선형성으로 인해 LRF 분포는 여전히 VAE latent 분포와 차이가 발생하여, LRF 렌더링 결과를 VAE 디코더를 통해 이미지로 다시 디코딩할 때 성능이 저하된다.
본 논문에서는 이러한 문제를 해결하기 위해 radiance field 정보를 활용하여 VAE 디코더를 fine-tuning하는 방법을 제안하였다. 구축한 LRF를 이용하여 대량의 장면으로부터 LRF를 재구성하고, 이를 통해 latent 이미지 쌍 데이터셋을 생성할 수 있다. 이 데이터셋은 LRF로 렌더링된 2D latent 표현 \(\mathcal{Z} = \{\textbf{Z}_i\}_{i=1}^K\)와 이에 대응하는 GT 이미지 \(\mathcal{I} = \{\textbf{I}_i\}_{i=1}^K\)로 구성된다. 특히, 기존 NVS 방법의 주요 특징 중 하나가 학습 뷰에 overfitting되는 것이기 때문에, 이 데이터셋에는 LRF의 학습 뷰도 포함하였다.
VAE-RF 정렬 디코더 fine-tuning의 학습 loss는 다음과 같다.
\[\begin{equation} \mathcal{L}_\textrm{StageIII} = \lambda_\textrm{train} \| D (Z_\textrm{train}) - I_\textrm{train} \|_1 + \lambda_\textrm{novel} \| D (Z_\textrm{novel}) - I_\textrm{novel} \|_1 \end{equation}\](\(\lambda_\textrm{train} = \lambda_\textrm{novel} = 0.5\))
Experiments
1. Latent 3D reconstruction
다음은 여러 데이터셋에서 렌더링 결과를 비교한 것이다.

다음은 다양한 데이터셋에서의 이미지 NVS와 latent space NVS 결과를 비교한 것이다.
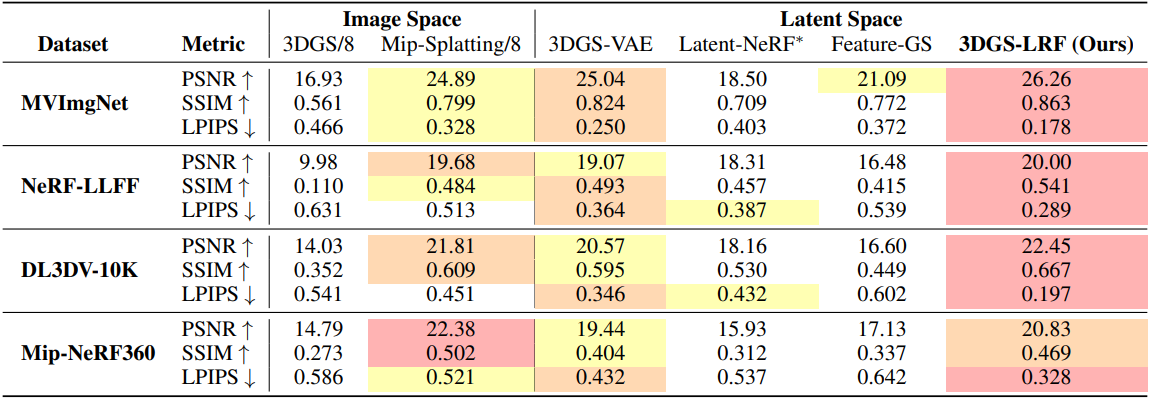
다음은 LLFF에서의 비교 결과이다. (3 view)
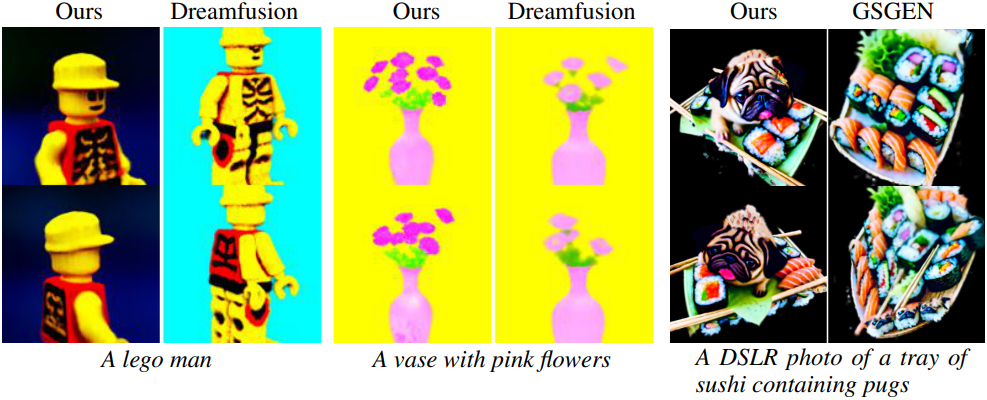
2. Text-to-3D generation
다음은 text-to-3D 생성 방법들과의 비교 결과이다.
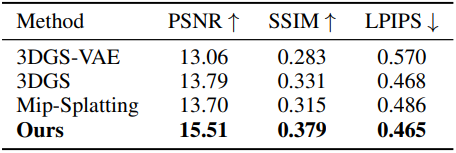
3. Ablation Study
다음은 fine-tuning 단계에 대한 ablation study 결과이다.

