[논문리뷰] Lotus: Diffusion-based Visual Foundation Model for High-quality Dense Prediction
ICLR 2025. [Paper] [Page] [Github]
Jing He, Haodong Li, Wei Yin, Yixun Liang, Leheng Li, Kaiqiang Zhou, Hongbo Zhang, Bingbing Liu, Ying-Cong Chen
HKUST(GZ) | University of Adelaide | Noah’s Ark Lab | HKUST
26 Sep 2024

Introduction
최근 연구에서는 zero-shot dense prediction을 위해 diffusion prior를 활용한다. 이러한 연구에서는 수십억 개의 이미지로 사전 학습된 Stable Diffusion과 같은 text-to-image diffusion model이 강력하고 포괄적인 visual prior를 가지고 있어 dense prediction 성능을 향상시킨다는 것을 보여주었다. 그러나 이러한 방법의 대부분은 더 적합한 diffusion 공식을 탐색하지 않고 dense prediction을 위해 사전 학습된 diffusion model을 직접 상속하였다. 이로 인해 종종 어려운 문제가 발생한다. 특히, 반복적인 denoising process와 앙상블 inferences로 인해 효율성이 심각하게 제한된다.
저자들은 diffusion 공식을 체계적으로 분석하여 사전 학습된 diffusion model을 dense prediction에 적합하게 하는 더 나은 공식을 찾으려고 노력했다. 분석 결과 몇 가지 중요한 결과가 도출되었다.
- Diffusion 기반 이미지 생성에 널리 사용되는 parameterization, 즉 noise 예측은 dense prediction에 적합하지 않다. 이는 초기 denoising step에서 유해한 예측 분산으로 인해 큰 예측 오차를 초래하며, 이는 이후 전체 denoising process에 걸쳐 전파되고 점점 오차가 커진다.
- Multi-step diffusion 공식은 계산 집약적이며 제한된 데이터와 리소스로 인해 최적이 아닌 경우가 많다. 이러한 요인은 diffusion prior를 dense prediction에 적용하는 것을 크게 방해하여 정확도와 효율성을 감소시킨다.
- 모델은 일반적으로 매우 디테일한 영역에서 모호한 예측을 출력하는 것으로 관찰되었다. 이러한 모호함은 catastrophic forgetting에 기인한다. 사전 학습된 diffusion model은 fine-tuning 중에 디테일한 영역을 생성하는 능력을 점차 잃는다.
분석 결과에 따라, 간단하면서도 효과적인 fine-tuning 프로토콜을 특징으로 하는 dense prediction을 위한 diffusion 기반 vision foundation model인 Lotus를 제안하였다. 먼저, Lotus는 주석을 직접 예측하도록 학습되어 표준 noise 예측과 관련된 유해한 분산을 방지한다. 다음으로, 순수 noise와 깨끗한 출력 사이가 1개의 timestep이 되도록 하여 모델 수렴을 촉진하고 제한된 고품질 데이터로 더 나은 최적화 성능을 달성하였다. 또한, 학습 및 inference 효율을 크게 향상시켰으며, task switcher를 통해 새로운 detail preserver를 구현하여 모델이 주석을 생성하거나 입력 이미지를 재구성할 수 있도록 하였다.
Lotus는 dense prediction 과정에서 입력 이미지의 세밀한 디테일을 더 잘 보존하여 효율성 저하, 추가 파라미터 필요성, 표면 텍스처의 영향 없이 더 높은 성능을 달성하였다.
Method
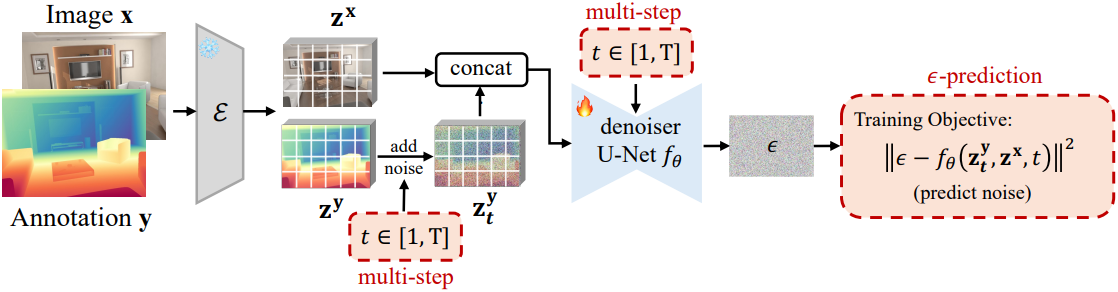
저자들은 위와 같은 구조로 최소한의 수정을 원래 diffusion 공식에 직접 적용하여 분석을 시작하였다. 이 시작점을 “Direct Adaptation”이라고 한다. Direct Adaptation은 만족스러운 성능을 달성하지 못하였다.
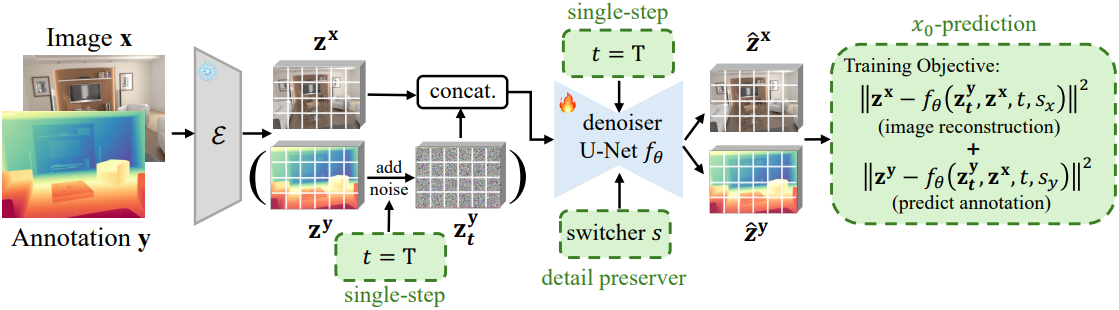
저자들은 적응 성능에 영향을 미치는 주요 요인을 단계별로 체계적으로 분석하였다.
1. Parameterization Types
Parameterization 유형은 매우 중요하다. Parameterization은 loss function을 결정할 뿐만 아니라 inference 과정에도 영향을 미친다.
\[\begin{aligned} \epsilon-\textrm{prediction}: & L_t^\epsilon = \| \epsilon - f_\theta^\epsilon (\textbf{z}_t^\textbf{y}, \textbf{z}^\textbf{x}, t) \|^2 x_0-\textrm{prediction}: & L_t^\textbf{z} = \| \textbf{z}^\textbf{y} - f_\theta^\textbf{z} (\textbf{z}_t^\textbf{y}, \textbf{z}^\textbf{x}, t) \|^2 \end{aligned}\]Inference 과정에서 예측된 깨끗한 샘플 \(\hat{\textbf{z}}_\tau^\textbf{y}\)는 parameterization에 따라 다르게 계산된다.
\[\begin{aligned} \epsilon-\textrm{prediction}: & \hat{\textbf{z}}_\tau^\textbf{y} = \frac{1}{\sqrt{\vphantom{1} \bar{\alpha}_\tau}} (\textbf{z}_\tau^\textbf{y} - \sqrt{1 - \bar{\alpha}_\tau} f_\theta^\epsilon (\textbf{z}_\tau^\textbf{y}, \textbf{z}^\textbf{x}, \tau)) \\ x_0-\textrm{prediction}: & \hat{\textbf{z}}_\tau^\textbf{y} = f_\theta^\textbf{z} (\textbf{z}_\tau^\textbf{y}, \textbf{z}^\textbf{x}, \tau) \end{aligned}\]일반적으로 이미지 생성의 표준은 $\epsilon$-prediction이다. 그러나 dense prediction task에서는 효과적이지 않다.
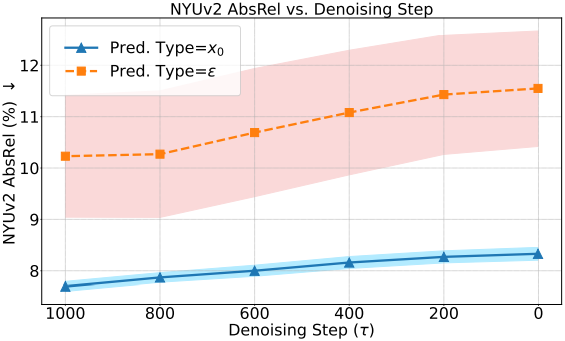
기존 논문들은 $\epsilon$-prediction이 특히 초기 denoising step(큰 $\tau$)에서 $x_0$-prediction에 비해 더 큰 픽셀 분산을 도입한다는 것을 보여주었다. 이 분산은 주로 noise 입력에서 발생한다. 구체적으로, 위의 $\epsilon$-prediction 식에서, $\tau \rightarrow T$일 때 \(\frac{1}{\sqrt{\vphantom{1} \bar{\alpha}_\tau}} \rightarrow +\infty\)이다. 따라서 \(f_\theta^\epsilon\)의 예측 분산이 상당히 증폭되어 예측된 \(\hat{\textbf{z}}_\tau^\textbf{y}\)의 분산이 커진다.
이와 대조적으로, $x_0$-prediction에는 모델 출력을 re-scaling하는 계수가 없어 초기 denoising step에서 \(\hat{\textbf{z}}_\tau^\textbf{y}\)가 더 안정적으로 예측된다. 이후 예측된 \(\hat{\textbf{z}}_\tau^\textbf{y}\)가 \(\textbf{z}_{\tau-1}^\textbf{y}\)의 계산에 사용된다.
\[\begin{equation} \textbf{z}_{\tau-1}^\textbf{y} = \sqrt{\vphantom{1} \bar{\alpha}_{\tau-1}} \hat{\textbf{z}}_\tau^\textbf{y} + \textrm{direction} (\textbf{z}_\tau^\textbf{y}) + \sigma_\tau \epsilon_\tau \end{equation}\]여기서 계수 \(\sqrt{\vphantom{1} \bar{\alpha}_{\tau-1}}\)은 두 parameterization에서 동일하고 다른 항들은 크기가 동일하다. 따라서 분산이 더 큰 $\epsilon$-prediction으로 예측된 \(\hat{\textbf{z}}_\tau^\textbf{y}\)는 denoising process에 더 큰 영향을 미친다. 이 과정은 반복적이기 때문에 이러한 영향은 지속적으로 유지되고 증폭될 수 있다.
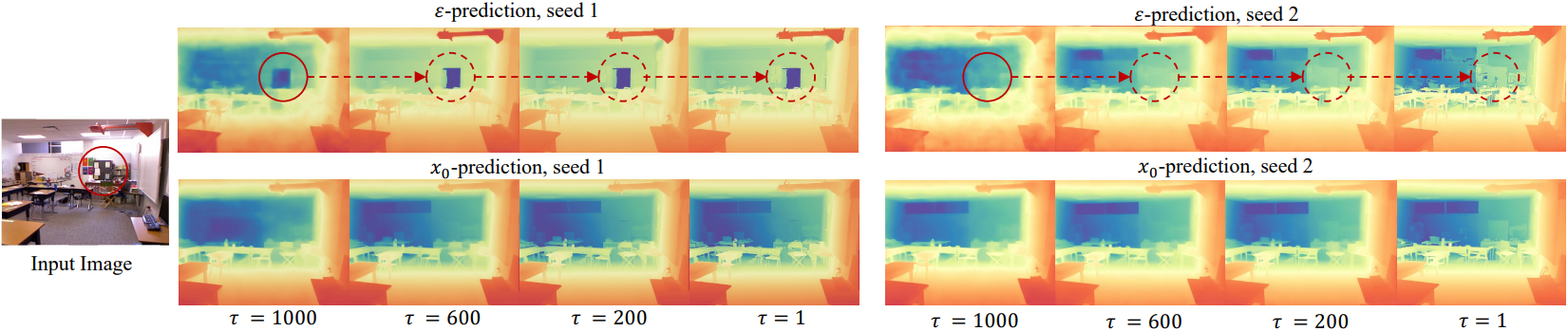
위 그림은 깊이 추정에서의 두 parameterization의 영향을 비교한 예시이다. $\epsilon$-prediction으로 예측된 depth map은 시드에 따라 상당히 달리지는 반면, $x_0$-prediction으로 예측된 depth map은 일관성이 더 높다. 분산이 크면 이미지 생성에 다양성이 높아지지만, dense prediction task에서는 예측이 불안정해져 상당한 오차가 발생할 가능성이 있다.
2. Number of Timesteps
$x_0$-prediction은 예측 품질을 향상시킬 수 있지만, multi-step diffusion 공식은 여전히 denoising process에서 예측된 오차의 확산을 초래한다. 이미지 생성과 같은 복잡한 task에서 여러 timestep을 사용하면 모델의 성능이 향상되며 최적화를 위해 일반적으로 대규모 학습 데이터가 필요하다. 그러나 dense prediction과 같이 대규모의 고품질 학습 데이터가 부족한 간단한 task의 경우, 여러 timestep을 사용하면 모델 최적화가 어려워질 수 있다. 또한, 학습 및 inference가 느리고 연산 집약적이어서 실제 적용이 어려워진다.
따라서 저자들은 사전 학습된 diffusion model을 더 적은 학습 timestep으로 fine-tuning하는 것을 제안하였다. 구체적으로, 원래 학습 timestep 집합이 \([1, T] = \{1, 2, \ldots, T\}\)로 정의될 때, 이 집합에서 파생된 부분 시퀀스를 사용하여 사전 학습된 diffusion model을 fine-tuning한다. 이 부분 시퀀스의 길이를 $T^\prime \le T$로 정의하며, 이 부분 시퀀스는 다음과 같이 원래 집합을 균등하게 샘플링하여 얻는다.
\[\begin{equation} \{t_i = i \cdot k \; \vert \; i = 1, 2, \ldots, T^\prime\} \end{equation}\]($k = T / T^\prime$는 샘플링 간격)
Inference 과정에서 DDIM은 $T^\prime \le 50$이면 동일한 하위 시퀀스를 사용하여 샘플의 noise를 제거하고, 그렇지 않으면 50개의 denoising step을 사용한다.
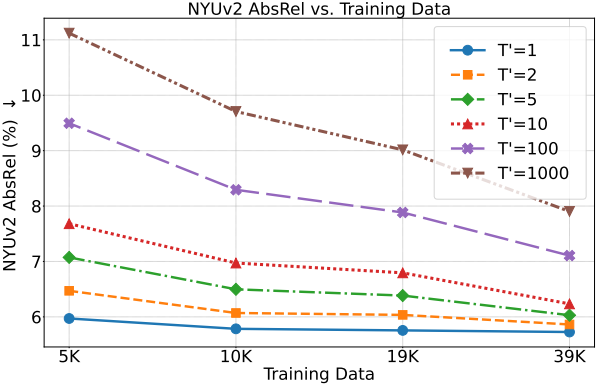
위 그림은 $x_0$-prediction에서 timestep의 수 $T^\prime$을 변화시켰을 때의 결과이다. 학습 데이터 규모에 관계없이 timestep 수가 줄어들수록 성능이 점진적으로 향상되고, 1개의 timestep으로 축소했을 때 최상의 결과를 얻었다.
Denoising step 수를 줄이면 diffusion model의 최적화 공간이 줄어들어, 더욱 효과적이고 효율적인 적응이 가능하다. 따라서 제한된 자원 하에서 더 나은 적응 성능을 위해, diffusion 공식의 학습 timestep 수를 하나로 줄이고 유일한 timestep $t$를 $T$로 고정한다. 또한, single-step 공식은 계산 효율이 훨씬 높으며, 유해한 오차 전파를 자연스럽게 방지하여 dense prediction에서 diffusion의 적응 성능을 더욱 향상시킨다.
3. Detail Preserver
위 설계의 효과에도 불구하고, 이 모델은 여전히 디테일한 영역의 처리에 어려움을 겪고 있다. 원래 diffusion model은 디테일한 이미지 생성에 탁월하다. 그러나 dense prediction에 적용하면 예상치 못한 catastrophic forgetting으로 인해 이러한 디테일한 이미지 생성 능력을 잃을 수 있다.
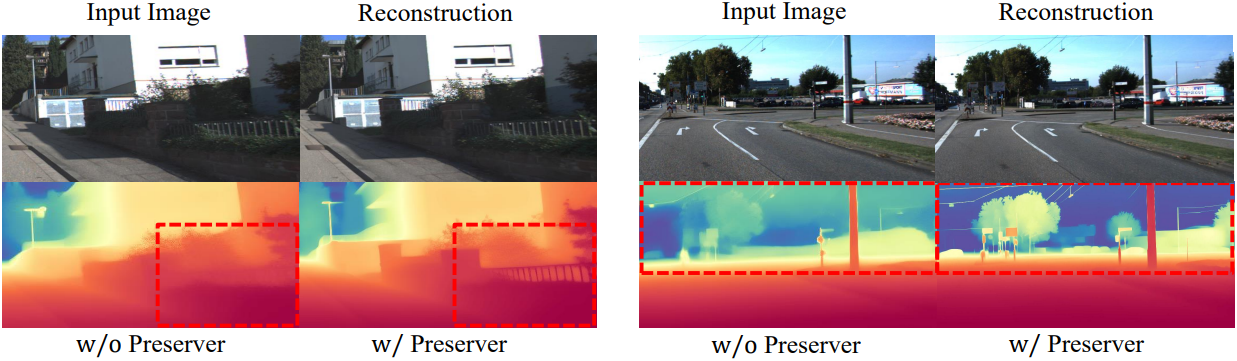
저자들은 입력 이미지의 풍부한 디테일을 보존하기 위해, Detail Preserver라는 새로운 정규화 전략을 도입했다. 구체적으로, task switcher \(s \in \{s_x, s_y\}\)를 활용하여 denoiser $f_\theta$가 주석을 생성하거나 입력 이미지를 재구성할 수 있도록 하였다. $s_y$가 선택되면 모델은 주석 예측에 집중한다. 반대로, $s_x$가 선택되면 모델은 입력 이미지를 재구성한다. Switcher $s$는 위치 인코더에 의해 인코딩된 1차원 벡터이며, 여기에 diffusion model의 시간 임베딩이 추가되어 상호 간섭 없이 원활한 도메인 전환을 보장한다. 이를 통해 diffusion model은 상세한 예측을 수행할 수 있어 더 나은 성능을 얻을 수 있다.
전반적으로 loss function $L_t$는 다음과 같다.
\[\begin{equation} L_t = \| \textbf{z}^\textbf{x} - f_\theta (\textbf{z}_t^\textbf{y}, \textbf{z}^\textbf{x}, t, s_x) \|^2 + \| \textbf{z}^y - f_\theta (\textbf{z}_t^\textbf{y}, \textbf{z}^\textbf{x}, t, s_y) \|^2 \end{equation}\]$t = T$이기 때문에 \(\textbf{z}_t^\textbf{y}\)는 순수한 Gaussian noise이다.
4. Stochastic Nature of Diffusion Model
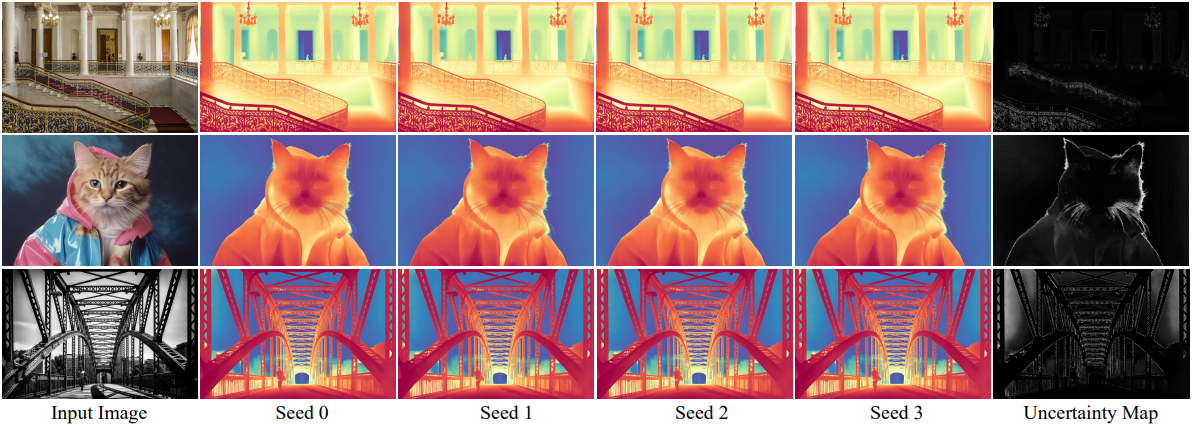
생성 모델의 주요 특징 중 하나는 확률적 특성으로, 이미지 생성 시 다양한 출력값을 생성할 수 있다는 점이다. Dense prediction과 같은 perception task에서 이러한 확률적 특성은 모델이 불확실성 맵을 사용하여 예측을 생성할 수 있도록 한다. 특히, 모든 입력 이미지에 대해 서로 다른 초기화 noise를 사용하여 여러 inference를 수행하고 이러한 예측을 종합하여 불확실성 맵을 계산할 수 있다. Lotus는 과도한 깜빡임(큰 분산)을 효과적으로 줄여 하늘, 물체 가장자리, 미세한 디테일과 같이 본질적으로 불확실한 영역에서만 더 정확한 불확실성 계산을 가능하게 한다.
대부분의 기존 perception model은 deterministic하다. 이러한 모델에 맞춰 noise 입력 \(\textbf{z}_t^\textbf{y}\)를 제거하고 인코딩된 이미지 feature \(\textbf{z}^\textbf{x}\)만을 U-Net denoiser에 입력할 수 있다. 이 모델은 여전히 좋은 성능을 보인다. Noise 입력을 사용하는 모델을 Lotus-G, noise 입력을 사용하지 않는 모델을 Lotus-D라고 부른다.
5. Inference
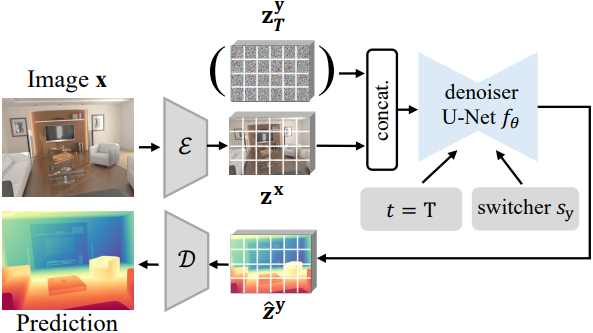
Inference 시에는 표준 Gaussian noise \(\textbf{z}_T^\textbf{y}\)로 주석 맵을 초기화하고, 입력 이미지를 latent code \(\textbf{z}^\textbf{x}\)로 인코딩한다. \(\textbf{z}_T^\textbf{y}\)와 \(\textbf{z}^\textbf{x}\)는 concat되어 U-Net denoiser에 입력된다. $t = T$로 설정하고 switcher를 $s_y$로 설정한다. 최종 주석 맵은 VAE 디코더를 통해 예측된 latent code에서 디코딩된다. Deterministic한 예측의 경우, Gaussian noise \(\textbf{z}_T^\textbf{y}\)를 제거하고 입력 이미지의 latent code만 U-Net에 입력한다.
Experiments
- 데이터셋: Hypersim (90%), Virtual KITTI (10%)
- Base model: Stable Diffusion V2
1. Quantitative Comparisons
다음은 zero-shot affine-invariant depth 추정 성능을 비교한 결과이다.
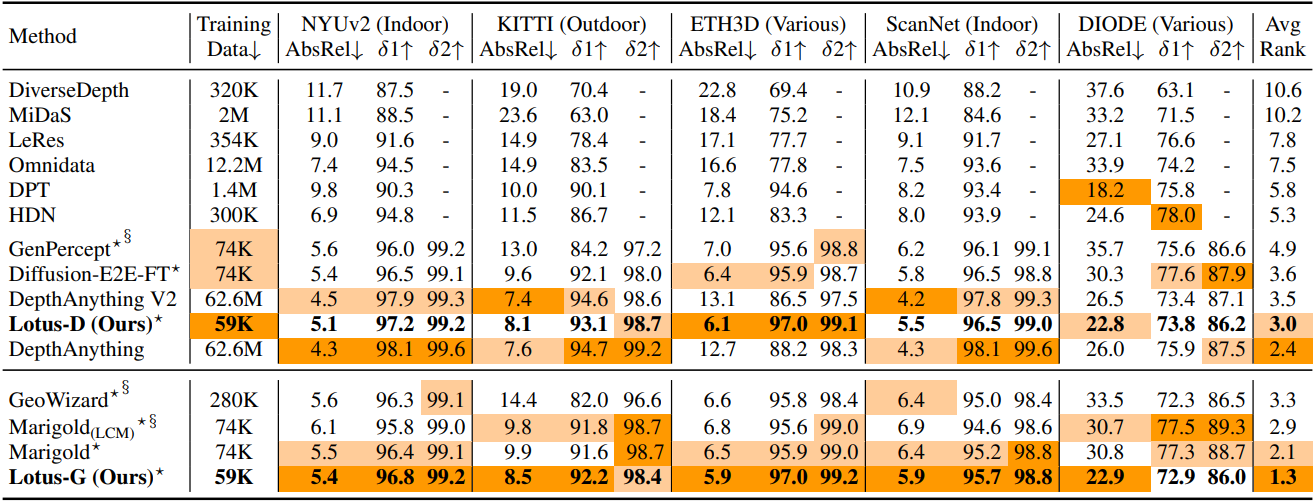
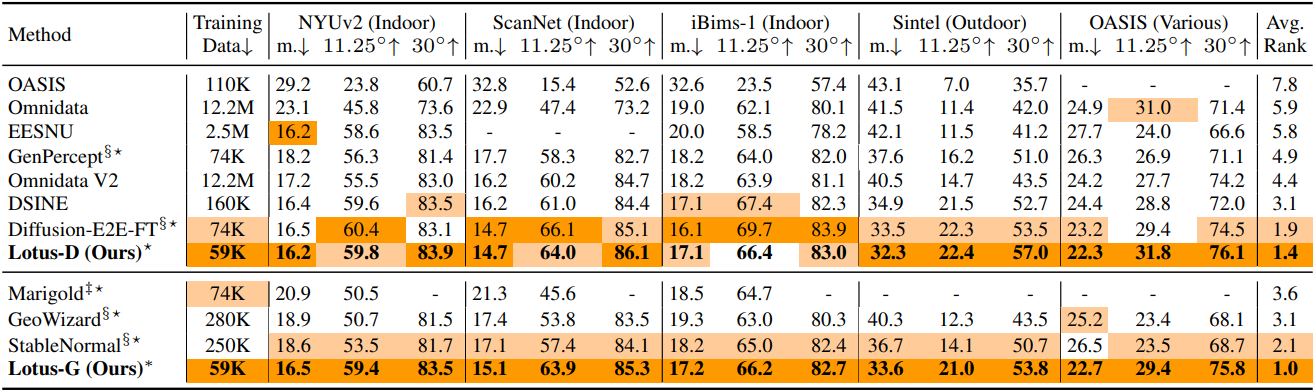
다음은 zero-shot normal 추정 성능을 비교한 결과이다.
2. Ablation Study
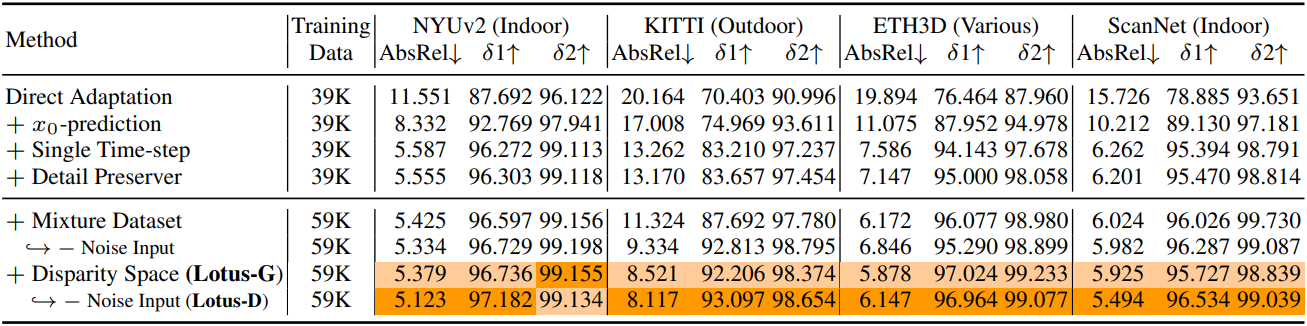
다음은 ablation study 결과이다.
다음은 detail preserver 유무에 따른 depth map을 비교한 예시이다.