[논문리뷰] LoRA3D: Low-Rank Self-Calibration of 3D Geometric Foundation Models

ICLR 2025 (Spotlight). [Paper] [Page]
Ziqi Lu, Heng Yang, Danfei Xu, Boyi Li, Boris Ivanovic, Marco Pavone, Yue Wang
NVIDIA Research | MIT | Harvard University | Georgia Institute of Technology | University of California, Berkeley | Stanford University | University of Southern California
10 Dec 2024

Introduction

최근, 많은 3D geometric foundation model들이 3D 재구성, 카메라 포즈 추정, 새로운 뷰 렌더링 등의 3D 컴퓨터 비전 task에 대한 잠재적 솔루션으로 등장했다. 이러한 모델들은 cross-view correspondence들을 빠르게 구축하고 sparse한 RGB 이미지들에서 3D 장면 형상을 직접 예측할 수 있다. 일반적으로 대규모 Transformer 사전 학습을 통해 광범위한 데이터로 일반화되기 때문에 새로운 task에서 강력한 zero-shot 성능을 보인다.

그러나 이러한 사전 학습된 모델의 성능은 어려운 상황에서 흔들릴 수 있다. 예를 들어, DUSt3R의 쌍별 재구성 정확도는 특정 영역이 하나의 시점에서만 관찰되는 경우에 상당히 저하된다. 이러한 성능 저하는 실제 3D 데이터의 분포를 완전히 표현하려면 훨씬 더 큰 규모의 데이터가 필요한 3D 형상 추론 task의 고유한 복잡성에 기인한다. 하지만, 실제 3D 데이터에 주석을 달기 어렵기 때문에 고품질 학습 데이터셋이 부족하여 사전 학습된 모델의 성능이 제한된다.

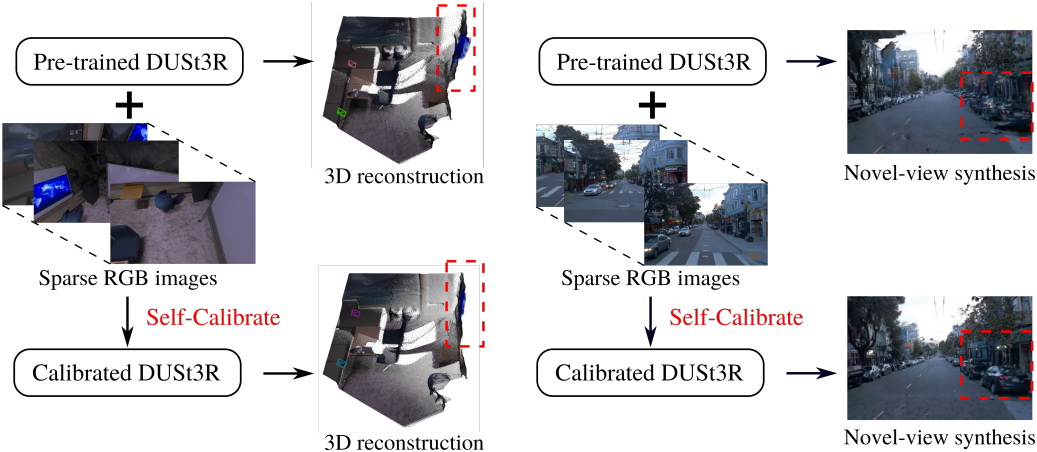
이 문제를 완화하기 위해, 본 논문은 효율적인 self-calibration을 제안하였다. Sparse한 RGB 이미지들만 사용하여 사전 학습된 3D foundation model을 대상 장면에 전문화하며, 수동 레이블링, 카메라 캘리브레이션, 또는 외부 prior가 필요하지 않다. 구체적으로, 3D 포인트 위치의 멀티뷰 일관성만을 활용하여 사전 학습된 모델의 예측을 정제하고 선택하여 pseudo-label을 생성한다. 저자들은 pseudo-label의 정확도를 보장하기 위해, 예측 신뢰도를 교정하는 동시에 멀티뷰 예측을 정렬하고 정제하는 robust한 global optimization 방법을 개발하였다. 교정된 신뢰도는 pseudo-label의 정확도와 강력하게 상관되므로, 사전 학습된 모델의 LoRA fine-tuning을 위한 높은 신뢰도의 데이터를 선택할 수 있게 해준다.

본 논문의 방법인 LoRA3D는 하나의 GPU에서 5분 안에 self-calibration 프로세스를 완료하고 최대 88%의 성능 향상을 제공할 수 있다.

Preliminaries

DUSt3R

DUSt3R는 RGB 이미지 쌍 $(I_i, I_j)$를 입력으로 사용하고 포인트 맵 $X^{i,i}, X^{j,i} \in \mathbb{R}^{H \times W \times 3}$과 신뢰도 맵 $C^{i,i}, C^{j,i} \in \mathbb{R}^{H \times W \times 1}$을 직접 예측한다.

\[\begin{equation} (X^{i,i}, C^{i,i}), (X^{j,i}, C^{j,i}) = \textrm{DUSt3R} (I_i, I_j) \end{equation}\]

$X^{i,i}, X^{j,i}$는 뷰 $i$와 뷰 $j$에 대한 포인트 맵으로, 둘 다 뷰 $i$의 카메라 좌표계에서 표현된다.

Recovering camera parameters

카메라 intrinsic은 예측된 포인트 맵에서 복구할 수 있다. 픽셀이 정사각형이고 principal point가 이미지 중심에 있는 핀홀 카메라 모델을 가정하면, 카메라 $i$의 초점 거리 $f_i$는 다음 최적화 문제를 풀어서 추정할 수 있다.

\[\begin{equation} f_i^\ast = \underset{f_i}{\arg \min} \sum_{p=1}^{HW} C_p^{i,i} \| ((u_p^\prime, v_p^\prime) - f_i \frac{(X_{p,0}^{i,i}, X_{p,1}^{i,i})}{X_{p,2}^{i,i}}) \| \\ \textrm{where} \; (u_p^\prime, v_p^\prime) = (u_p - W/2, v_p - H/2) \end{equation}\]

상대적인 카메라 포즈는 이미지 쌍 $(I_i, I_j)$와 $(I_j, I_i)$에 대한 예측을 비교하여 추정된다. 포인트 맵 $X^{i,i}$와 $X^{i,j}$를 사용하면 카메라 $i$에서 $j$로의 상대적 포즈 $T_{i,j} \in \textrm{SE}(3)$과 포인트 맵 스케일 \(\sigma_{i,j}\)를 추정할 수 있다.

\[\begin{equation} (T^{(i,j)}, \sigma^{(i,j)})^\ast = \underset{T^{(i,j)}, \sigma^{(i,j)}}{\arg \min} \sum_p C_p^{i,i} C_p^{i,j} \| \sigma^{(i,j)} T^{(i,j)} X_p^{i,i} - X_p^{i,j} \|^2 \end{equation}\]

Multi-view point map alignment

DUSt3R는 글로벌 포인트 맵 $\chi$와 변환된 예측 포인트 맵 사이의 3D-3D projection error를 최소화하여 초기 추정치를 정제한다.

\[\begin{equation} (\chi, T, \sigma)^\ast = \underset{\chi, T, \sigma}{\arg \min} \sum_{(i,j) \in \mathcal{E}} \sum_{v \in \{i,j\}} \sum_{p=1}^{HW} C_p^{v,i} \| \chi_p^v - \sigma^{(i,j)} T^{(i,j)} X_p^{v,i} \| \end{equation}\]

글로벌 포인트 맵 $\chi_p^v$는 depth back-projection을 통해 다음과 같이 나타낼 수 있다.

\[\begin{equation} \chi_p^v = T_v K_v^{-1} D_p (u_p, v_p, 1)^\top = T_v \frac{D_p}{f_v} (u_p^\prime, v_p^\prime, 1)^\top \end{equation}\]

($K_v$와 $T_v$는 뷰 $v$의 intrinsic과 extrinsic, $D_p$는 픽셀 $p$의 깊이 값)

따라서 최적화 문제는 다음과 같이 다시 쓸 수 있다.

\[\begin{equation} (T, \sigma, f, D)^\ast = \underset{T, \sigma, f, D}{\arg \min} \sum_{(i,j) \in \mathcal{E}} \sum_{v \in \{i,j\}} \sum_{p=1}^{HW} C_p^{v,i} \| T_v \frac{D_p}{f_v} (u_p^\prime, v_p^\prime, 1)^\top - \sigma^{(i,j)} T^{(i,j)} X_p^{v,i} \| \end{equation}\]

이미지 쌍별 포즈 $T^{(i,j)}$와 이미지별 포즈 $T_i$는 동일한 변환을 나타내지만 추가적인 최적화 유연성을 위해 별도로 존재한다. 최적화는 gradient descent로 진행되며, $\sigma^{(i,j)} = 0$을 피하기 위해 최적화 중에 \(\prod_{(i,j)} \sigma^{(i,j)} = 1\)이 적용된다.

Method

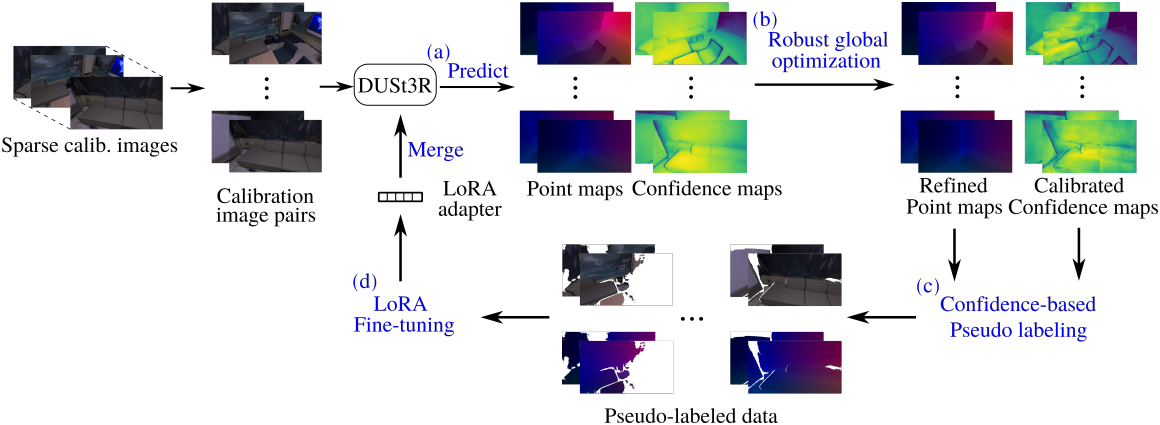
1. Self-calibration pipeline

먼저, 사전 학습된 DUSt3R를 사용하여 모든 이미지 쌍에 대한 포인트 맵과 신뢰도 맵을 예측하는 것으로 시작한다. 카메라 뷰가 적게 겹치는 경우에서 DUSt3R의 예측에는 오차와 outlier가 포함될 수 있으며 예측된 신뢰도는 예측의 정확도를 정확하게 반영하지 않을 수 있다. 따라서, pseudo-label 선택을 예측된 신뢰도에 직접 의존하면 모델 성능이 저하될 수 있다.

그러나 장면의 각 3D 포인트는 많은 카메라 뷰 쌍에 의해 공동 관찰된다. 즉, 정확한 DUSt3R 예측을 활용하여 부정확한 포인트 맵 예측을 정제하고 식별할 수 있다. 따라서, 저자들은 포인트 맵을 최적화하고 예측 신뢰도를 교정하기 위해 강력한 멀티뷰 포인트 맵 정렬 방법을 개발하였다. 그런 다음, 정제된 포인트 맵과 교정된 신뢰도를 사용하여 이미지 \(\{I_i\}_{i=1}^N\)에 pseudo-label을 만든 다음, pseudo-label이 생긴 데이터에 LoRA를 사용하여 사전 학습된 DUSt3R 모델을 fine-tuning하였다.

2. Robust multi-view point map alignment with confidence calibration

저자들은 글로벌 최적화에 예측된 신뢰도를 통합하여 robust한 멀티뷰 포인트 맵 정렬 방법을 개발하였다. 구체적으로, 원래 최적화 식에서 신뢰도 항 $C_p^{v,i}$최적화 가능한 가중치 항 $w_p^{v,i}$로 re-parameterize하여 각 포인트 예측이 최적화에 기여하는 정도를 자동으로 조정한다. 예측된 신뢰도는 부정확할 수 있지만 예측 정확도에 대한 정보는 여전히 있다. 따라서, 가중치가 예측 신뢰도에 가깝게 유지되도록 장려하고 자명한 해를 피하는 정규화 항을 도입하는 것이 목표이다.

저자들은 이 목표가 Geman-McClure robust M-estimator와 상당히 일치한다는 것을 발견했다. 이는 본질적으로 최소제곱 최적화에서 가중치가 1에 가깝도록 유도하는 정규화 항을 사용하는 방식이다. 이에 영감을 얻어, 저자들은 유사한 구조를 따르도록 정규화 항을 설계했다. 따라서 원래 최적화 식은 다음과 같이 다시 쓸 수 있다.

\[\begin{equation} (T, \sigma, f, D, \mathcal{W})^\ast = \underset{T, \sigma, f, D, \mathcal{W}}{\arg \min} \sum_{(i,j) \in \mathcal{E}} \sum_{v \in \{i,j\}} \sum_{p=1}^{HW} w_p^{v,i} \| e_p^{v,i} \| + \mu (\sqrt{w_p^{v,i}} - \sqrt{C_p^{v,i}})^2 \\ \textrm{where} \quad e_p^{v,i} = T_v \frac{D_p}{f_v} (u_p^\prime, v_p^\prime, 1)^\top - \sigma^{(i,j)} T^{(i,j)} X_p^{v,i} \end{equation}\]

Gradient back-propagation을 통해 위 식의 가중치를 업데이트하는 대신, 저자들은 빠른 신뢰도 재가중을 위한 closed-form 가중치 업데이트 규칙을 도출하였다.

\[\begin{equation} w_p^{v,i} = \frac{C_p^{v,i}}{(1 + \| e_p^{v,i} \| / \mu)^2} \end{equation}\]

이 업데이트 규칙을 사용하면 주기적으로 가중치 업데이트를 적용하는 동안 원래 최적화 문제를 여전히 풀 수 있다.

Residual error $e_p^{v,i}$가 낮은 포인트 예측, 즉 다른 이미지 쌍의 예측과 더 일관성이 있는 포인트 예측은 예측된 값과 유사한 신뢰도를 유지한다. 반면, 뷰 간에 일관되지 않은 포인트 예측은 신뢰도가 상당히 감소한다. 아래 그림에서 볼 수 있듯이, 이 방법은 지나치게 신뢰도가 높은 예측에 대한 신뢰도를 효과적으로 최소화하여 신뢰도가 포인트 추정 정확도와 더 긴밀하게 상관되며, 글로벌 최적화 및 pseudo-label 생성에 대한 더 나은 guidance를 제공한다.

3. Multi-view point map alignment

Pseudo-label을 만들기 위해 교정된 신뢰도와 최적화된 포인트 맵을 사용한다. 이미지 쌍에 대한 pseudo-label을 계산하려면 글로벌 최적화 결과를 로컬 이미지 쌍 좌표 프레임으로 변환해야 한다. 구체적으로, 최적화된 depth map $D_p$를 3D로 back-projection하고 포인트를 이미지 쌍 좌표 프레임으로 변환한다. 그런 다음, 신뢰도가 threshold \(w_\textrm{cutoff}\)보다 높은 포인트들을 pseudo-label로 유지한다.

\[\begin{equation} \tilde{X}_p^{j,i} = T_i^{\ast -1} T_j^\ast \frac{D_p^\ast}{f_j^\ast} (u_p^\prime, v_p^\prime, 1)^\top, \quad \textrm{where} \; p \in \{p \vert w_p^{\ast j,i} > w_\textrm{cutoff}\} \end{equation}\]

\(w_\textrm{cutoff} = 1.5\)로 설정하면 대부분의 장면에서 효과적으로 작동한다고 한다. 동적인 포인트는 멀티뷰 일관성 가정을 깨기 때문에 pseudo-label을 생성할 때 자동으로 필터링되며, 이로 인해 LoRA3D는 장면의 동적 물체에 robust하다.

4. Fine-tuning with LoRA

Pseudo-label이 생긴 데이터에 대하여, DUSt3R와 동일한 사전 학습 loss를 사용하여 LoRA를 포함한 사전 학습된 DUSt3R를 fine-tuning한다.사전 학습된 DUSt3R의 가중치는 고정되며, LoRA는 학습 가능한 rank decomposition 행렬을 Transformer 아키텍처 레이어에 주입하여 학습 가능한 파라미터 수를 크게 줄인다. 이는 self-calibration의 런타임 및 메모리 효율성을 개선하고, 사전 학습 데이터에 대한 catastrophic forgetting을 줄인다.

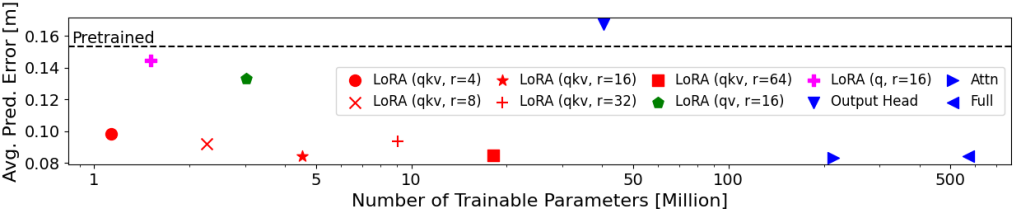
최적의 DUSt3R fine-tuning 전략을 찾기 위해, 저자들은 여러 테스트 장면에서 다양한 fine-tuning 옵션을 비교하기 위해 광범위한 실험을 수행했다. 위의 실험 결과에서 볼 수 있듯이, 모든 attention 가중치를 rank-16 LoRA로 fine-tuning하면 성능과 효율성 간에 최상의 균형을 이룰 수 있다. Attention이나 모든 가중치를 직접 fine-tuning하는 것과 비교했을 때, LoRA fine-tuning은 학습 가능한 파라미터 수를 99% 이상 줄이면서 동일한 성능을 보인다.

Rank-16 LoRA를 사용하여 10개의 이미지에 대한 fine-tuning은 batch size 2로 3.5분 이내에 수렴하며, fine-tuning 중 최대 GPU 메모리 사용량은 20GB 미만으로 유지된다. 각 LoRA 어댑터는 18MB 미만의 저장 공간이 필요하다.

Experiments

• Pretrain: 사전 학습된 DUSt3R
• Self-Calib: Pretrain에 self-calibration을 적용한 모델
• GT-FT: Pretrain을 GT 포인트맵으로 fine-tuning한 모델 (Self-Calib의 상한, oracle)

1. Results

다음은 Replica 데이터셋에서의 (위) 쌍별 재구성 결과와 (아래) 멀티뷰 재구성 결과이다.

다음은 (a, b) Replica와 (c, d) TUM RGBD의 장면에서 self-calibration 전후의 재구성 결과를 비교한 예시들이다.

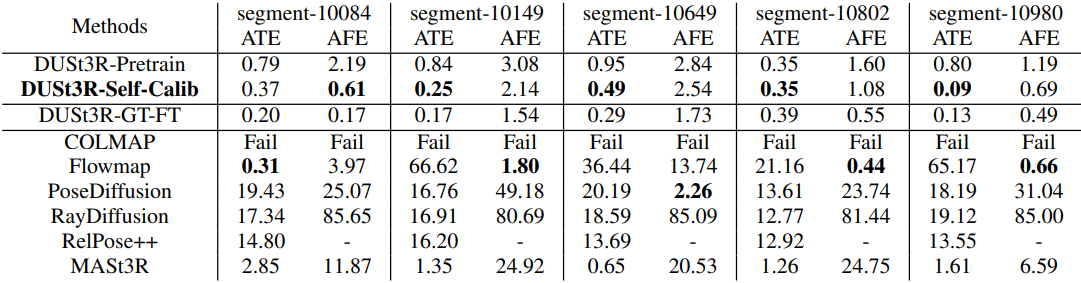
다음은 Waymo Open Dataset에서 absolute trajectory error (m)와 and average focal error (%)를 비교한 표이다.

다음은 DUSt3R self-calibration 전후의 InstantSplat에 의한 새로운 뷰 렌더링 결과이다. (Waymo Open Dataset)

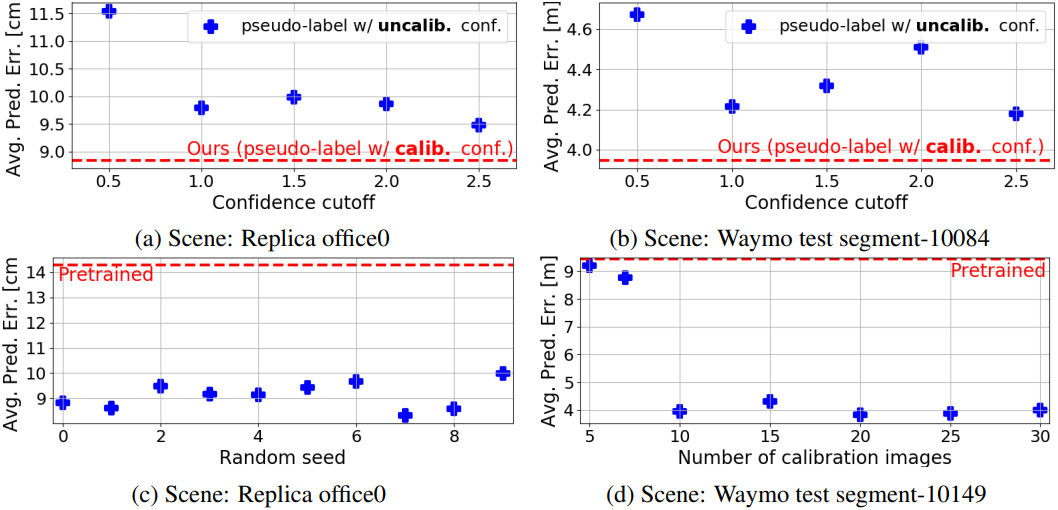
2. Ablation Study

다음은 ablation 결과이다. (a, b)는 교정되지 않은 신뢰도를 pseudo-label로 사용한 경우에 대한 비교이고, (c)는 랜덤 시드, (d)는 글로벌 최적화에 사용된 이미지의 수에 대한 비교이다.