[논문리뷰] LongNet: Scaling Transformers to 1,000,000,000 Tokens

arXiv 2023. [Paper] [Github]
Jiayu Ding, Shuming Ma, Li Dong, Xingxing Zhang, Shaohan Huang, Wenhui Wang, Nanning Zheng, Furu Wei
Microsoft Research | Xi’an Jiaotong University
5 Jul 2023

Introduction

최근 몇 년 동안 신경망 스케일링 트렌드가 나타났다. 깊이는 주로 기하급수적 표현을 위해 확장되어 많은 강력한 심층 네트워크를 생성한다. 그런 다음 sparse MoE model과 모델 병렬 처리 방식이 hidden 차원을 효율적으로 확대한다. 신경망의 시퀀스 길이는 무제한인 것이 바람직하다. 시퀀스 길이의 한계를 깨면 상당한 이점이 있다.

1. 모델에 큰 메모리와 receptive field를 제공하여 모델이 사람과 상호 작용하는 데 실용적이다.
2. 더 긴 컨텍스트에는 모델이 학습 데이터에서 활용할 수 있는 더 복잡한 인과 관계와 추론 경로가 포함된다. 대조적으로, 짧은 의존성은 더 허위 상관관계를 가지므로 일반화에 해롭다.
3. 매우 긴 컨텍스트는 모델이 치명적인 망각을 완화하는 데 도움이 될 수 있기 때문에 many-shot learning의 패러다임 전환이 될 가능성이 있는 in-context learning의 한계를 탐색할 수 있다.

시퀀스 길이를 확장하는 데 있어 가장 큰 과제는 계산 복잡도와 모델 표현성 사이의 적절한 균형을 맞추는 것이다. RNN 스타일 모델은 주로 길이를 늘리기 위해 구현된다. 그러나 순차적 특성으로 인해 학습 중 병렬화가 제한되며, 이는 긴 시퀀스 모델링에 필수적이다. 최근에는 상태 공간 모델이 시퀀스 모델링에 매력적이다. 학습 중에는 CNN으로 작동하고 테스트 시 효율적인 RNN으로 변환할 수 있다. 장거리 벤치마크에서는 좋은 성능을 발휘하지만 일반 길이에서의 성능은 주로 모델 표현력에 의해 제한되는 Transformer만큼 좋지 않다.

시퀀스 길이를 확장하는 또 다른 방법은 Transformer의 복잡도, 즉 self-attention의 2차 복잡도를 줄이는 것이다. Attention을 위해 sliding window나 convolution 모듈을 구현하는 것은 복잡도를 거의 선형으로 만드는 간단한 방법이다. 그럼에도 불구하고 이는 초기 토큰을 기억하는 능력을 희생하고 시퀀스 시작 부분의 프롬프트를 잊어버린다. Sparse attention은 attention 행렬을 희소화(sparsify)하여 계산을 줄이고 장거리 정보를 회상할 가능성을 보존한다. 예를 들어, 고정된 sparse 패턴을 사용하면 $O(N \sqrt{N} d)$의 시간 복잡도를 얻는다. 휴리스틱 패턴 외에도 학습 가능한 패턴은 sparse attention에 유용한 것으로 입증되었다. low-rank attention, 커널 기반 방법, 다운샘플링 접근 방식, recurrent model,검색 기반 방법을 포함하는 다른 효율적인 Transformer 기반 변형도 있다. 그러나 10억 개의 토큰으로 확장된 경우는 없다.

본 논문에서는 시퀀스 길이를 10억 개의 토큰으로 성공적으로 확장했다. 본 논문의 솔루션은 바닐라 Transformer의 attention을 dilated attention이라는 새로운 구성 요소로 대체하는 LongNet이다. 일반적인 디자인 원칙은 토큰 사이의 거리가 증가함에 따라 attention 할당이 기하급수적으로 감소한다는 것이다. LongNet은 선형 계산 복잡도와 토큰 간의 로그 의존성을 얻었다. 이는 제한된 attention 자원과 모든 토큰에 대한 접근성 사이의 모순을 다룬다. 구현 시 LongNet은 Transformer에 대한 기존 최적화 (ex. 커널 융합, quantization, 분산 학습)를 원활하게 지원하는 고밀도 Transformer로 변환될 수 있다. 선형 복잡도를 활용하여 LongNet은 노드 전체에 걸쳐 학습을 병렬화하여 분산 알고리즘을 통해 계산과 메모리의 제약을 깨뜨릴 수 있다. 이를 통해 거의 일정한 런타임으로 시퀀스 길이를 10억 토큰까지 효율적으로 확장할 수 있다.

LongNet

1. Preliminary

Transformers의 핵심은 qury, key, value 집합을 출력에 매핑하는 self-attention이다. 입력 $Q, K, V \in \mathbb{R}^{N \times d}$가 주어지면 출력 $O$를 다음과 같이 계산한다.

\[\begin{equation} O = \textrm{softmax} (QK^\top) V \end{equation}\]

Self-attention은 시퀀스 길이에 대한 2차 의존성으로 인해 긴 시퀀스에서 어려움을 겪는다. 하나의 query가 모든 key와 valye를 처리하므로 계산상의 비효율성이 발생한다.

Sparse attention은 query의 액세스를 key와 value의 부분 집합으로 제한하여 이 문제를 완화한다. Sparse attention의 핵심은 sparse attention 패턴 \(S \in \{0, 1\}^{N \times N}\)이며, 이는 query $Q$가 attend할 수 있는 특정 key와 value를 결정한다.

\[\begin{equation} O = \textrm{softmax} (QK^\top \odot \unicode{x1D7D9}_S ) V \end{equation}\]

예를 들어 sparse Transformer의 고정 패턴은 로컬 패턴과 strided 패턴으로 구성된다. 시퀀스는 길이가 l인 블록으로 나뉜다. 로컬 패턴을 사용하면 하나의 query가 동일한 블록 내의 토큰에 attend할 수 있는 반면, strided 패턴에서는 하나의 query가 각 블록의 마지막 $c$개의 토큰에 attend할 수 있다. 로컬 패턴 $S_i^{(1)}$과 strided 패턴 $S_2^{(2)}$는 다음과 같이 정의된다.

\[\begin{aligned} S_i^{(1)} &= \{ j \; \vert \; \lfloor j/l \rfloor = \lfloor i/l \rfloor \} \\ S_i^{(2)} &= \{ j \; \vert \; j \textrm{ mod } l \in \{t, t+1, \ldots, l \}\} \end{aligned}\]

2. Dilated Attention

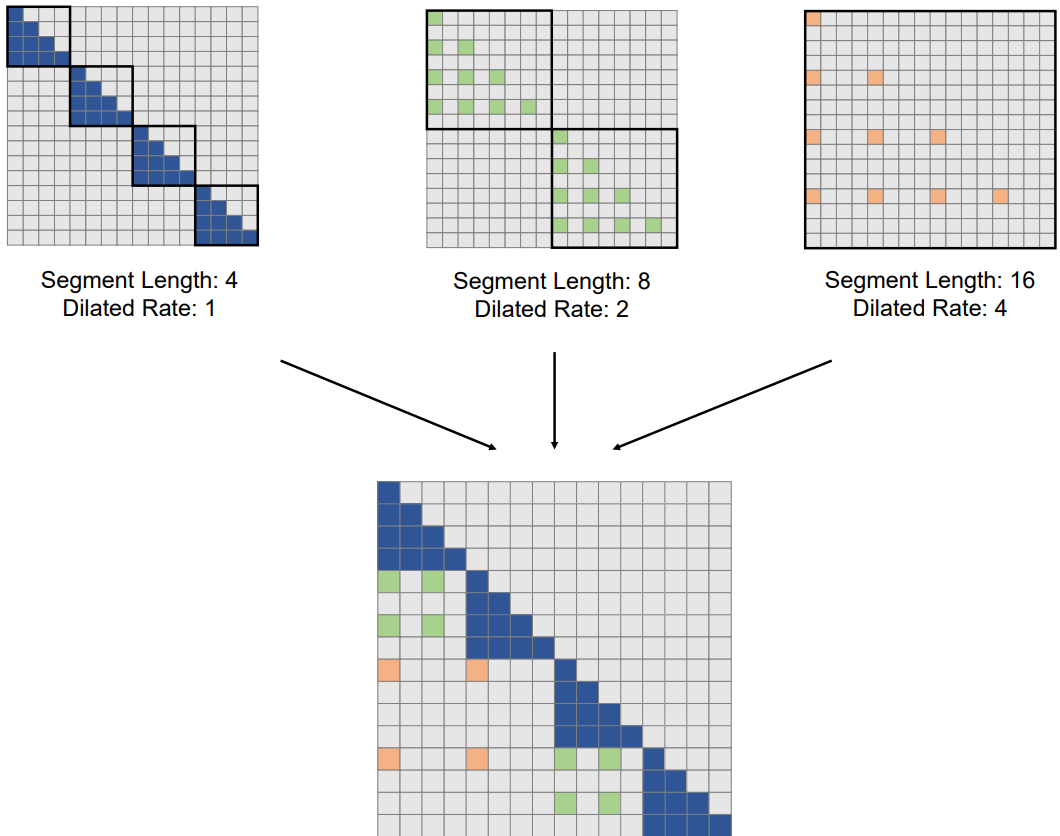
위 그림은 dilated attention의 개요를 보여준다. Dilated attention은 입력 $(Q, K, V)$를 세그먼트 길이 $w$와 동일하게 세그먼트 \(\{(\tilde{Q}_i, \tilde{K}_i, \tilde{V}_i)\}^{\frac{N}{w}}\)로 분할한다. 그런 다음 각 세그먼트는 간격 $r$을 사용하여 행을 선택하여 시퀀스 차원을 따라 sparsify된다. 계산은 다음과 같다.

\[\begin{equation} \tilde{Q}_i = [Q_{iw}, Q_{iw+r}, Q_{iw+2r}, \ldots, Q_{(i+1)w - 1}] \\ \tilde{K}_i = [K_{iw}, K_{iw+r}, K_{iw+2r}, \ldots, K_{(i+1)w - 1}] \\ \tilde{V}_i = [V_{iw}, V_{iw+r}, V_{iw+2r}, \ldots, V_{(i+1)w - 1}] \end{equation}\]

Sparsify된 세그먼트 \(\{(\tilde{Q}_i, \tilde{K}_i, \tilde{V}_i)\}^{\frac{N}{w}}\)는 병렬로 attention에 공급된 후 출력 O로 분산되고 concat된다.

\[\begin{equation} \tilde{O}_i = \textrm{softmax} (\tilde{Q}_i \tilde{K}_i^\top) \tilde{V}_i \\ \hat{O}_i = \{ \tilde{O}_{i,j} \vert j \textrm{ mod } r = 0; \; 0 \vert j \textrm{ mod } r \ne 0 \} \\ O = [\hat{O}_0, \hat{O}_1, \ldots, \hat{O}_{\frac{N}{w} - 1}] \end{equation}\]

구현에서 dilated attention은 입력 $(Q, K, V)$에 대한 gathering 연산과 출력 \(\tilde{O}_i\)에 대한 scattering 연산 사이에서 dense attention으로 변환될 수 있으므로 바닐라 attention에 대한 최적화를 직접 재사용할 수 있다. Dilated attention은 바닐라 attention에 비해 $\frac{N}{w} r^2$만큼 계산 비용을 크게 줄일 수 있다.

실제로 세그먼트 크기 $w$는 효율성을 위해 attention의 globality를 교환하는 반면, 크기 $r$을 사용한 dilation은 attention 행렬을 근사화하여 계산 비용을 줄인다. 장거리 정보와 단거리 정보를 모두 효율적으로 캡처하기 위해 다양한 dilation rate와 세그먼트 크기 \(\{r_i , w_i\}^k\)를 갖는 dilated attention의 혼합을 구현한다.

\[\begin{equation} O = \sum_{i=1}^k \alpha_i O \vert_{r_i, w_i} \\ \alpha_i = \frac{s_i}{\sum_j s_j} \end{equation}\]

여기서 $s_i$는 $O \vert_{r_i, w_i}$에 대한 attention softmax의 분모를 나타낸다. \(\{O \vert_{r_i, w_i}\}^k\)에 대한 계산은 계산 의존성이 없기 때문에 병렬이다. 실험에 따르면 attention softmax의 분모로 계산된 동적 가중치가 학습 가능한 고정 가중치보다 더 나은 것으로 나타났다. Query가 서로 다른 dilated attention의 key에 attend할 경우 dilated attention을 혼합하는 방법은 서로 다른 부분의 key를 수집하고 함께 softmax를 계산하는 것과 동일하다.

직관적으로 로컬 attention은 정확하게 계산되어야 하지만 글로벌 attention은 대략적으로 계산될 수 있다. 그러므로 더 큰 $r_i$로 더 큰 $w_i$를 설정한다. 또한, 최대 길이 $N$ 또는 attention 패턴 수 $k$에 도달할 때까지 각 attention에 대한 $w_i$를 점차적으로 늘린다.

\[\begin{equation} w = \{ w_0, w_1, \ldots, N \}^k \quad (w_i < w_{i+1} < N) \\ r = \{ 1, r_1, r_2, \ldots, r_k \}^k \quad (1 < r_i < r_{i+1}) \end{equation}\]

실제로 저자들은 exponential attentive field에 대한 기하학적 시퀀스로 $w$와 $r$을 설정했다.

3. Multi-Head Dilated Attention

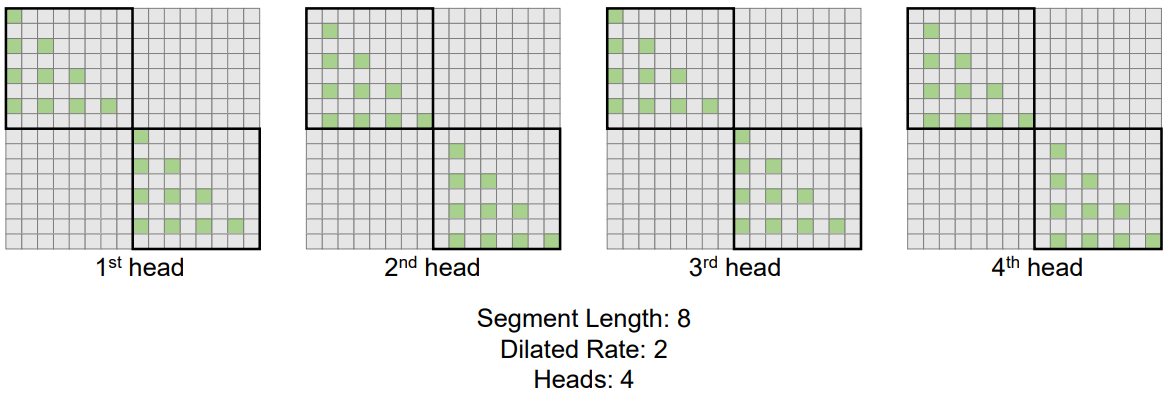
위 그림에서 볼 수 있듯이 query-key-value 쌍의 서로 다른 부분을 sparsify하여 서로 다른 head 간의 계산이 다르다. 구체적으로, $j$번째 헤드의 경우 $(Q, K, V)$를 선택할 때 오프셋 $s_j = j \textrm{ mod } r$이 존재한다.

\[\begin{equation} \tilde{Q}_i = [Q_{iw + s_j}, Q_{iw + s_j + r}, Q_{iw + s_j + 2r}, \ldots, Q_{(i+1)w + s_j - 1}] \\ \tilde{K}_i = [K_{iw + s_j}, K_{iw + s_j + r}, K_{iw + s_j + 2r}, \ldots, K_{(i+1)w + s_j - 1}] \\ \tilde{V}_i = [V_{iw + s_j}, V_{iw + s_j + r}, V_{iw + s_j + 2r}, \ldots, V_{(i+1)w + s_j - 1}] \end{equation}\]

바닐라 multi-head attention을 따라, 서로 다른 head의 출력이 최종 출력으로 concat된다. 나머지 계산은 단일 head 계산과 동일하게 유지된다.

4. Computational Complexity and Token Dependency

Dilation rate와 세그먼트 크기가 $(r, w)$인 dilated attention이 주어지면 각 query-key-value 쌍은 $(Q, K, V) \in \mathbb{R}^{N \times d}$에서 $(Q, K, V) \in \mathbb{R}^{\frac{w}{r} \times d}$로 sparsify된다. 따라서 attention 계산의 flops는 다음과 같이 추정된다.

\[\begin{equation} \textrm{FLOPs} = \frac{2N}{w} (\frac{w}{r})^2 d = \frac{2Nwd}{r^2} \end{equation}\]

이를 다양한 세그먼트 크기와 dilation rate의 dilated attention으로 확장한다. Flops은 다음과 같다.

\[\begin{equation} \textrm{FLOPs} = 2Nd \sum_{i=1}^k \frac{w_i}{r_i^2} \end{equation}\]

세그먼트 크기와 dilation rate의 대소관계를 사용하면 flops는 다음과 같이 계산된다.

\[\begin{equation} \textrm{FLOPs} = 2w_0 Nd \sum_{i=0}^{k-1} \frac{1}{\alpha^i} \le \frac{2 \alpha}{\alpha - 1} w_0 Nd \quad (\alpha > 1) \end{equation}\]

여기서 $w_0$는 미리 정의된 상수이고 $\alpha$는 기하학적 시퀀스 $w$와 $r$의 공통 비율이다. 따라서 dilated attention의 계산 복잡도는 $O(Nd)$에 가깝다.

또한 각 토큰의 정보는 최대 거리 $D$까지 전파될 수 있다.

\[\begin{equation} D = \sum_{i=0}^{l-1} w_i = w_0 \sum_{i=0}^{l-1} \alpha^i \approx \frac{w_0}{\alpha - 1} \alpha^l \end{equation}\]

여기서 $l$은 전파 경로의 길이이다. 따라서 $N$개의 토큰이 있는 시퀀스의 최대 경로 길이는 다음과 같이 추정할 수 있다.

\[\begin{equation} L \approx \log_\alpha \frac{N (\alpha - 1)}{w_0} \quad (\alpha > 1) \end{equation}\]

이는 토큰 의존성이 $O(\log N)$에 가깝다는 것을 증명한다.

LongNet as a Distributed Trainer: Scaling up to 1B Tokens

Dilated attention의 계산 복잡도가 $O(Nd)$로 크게 감소했음에도 불구하고 계산 및 메모리 제약으로 인해 단일 GPU 장치에서 시퀀스 길이를 백만 수준으로 확장하는 것은 불가능하다. 모델 병렬성, 시퀀스 병렬성, 파이프라인 병렬성과 같은 대규모 모델 학습을 위한 분산형 학습 알고리즘이 있다. 그러나 특히 시퀀스 차원이 매우 큰 경우 LongNet에는 충분하지 않는다.

1. Distributed Algorithm

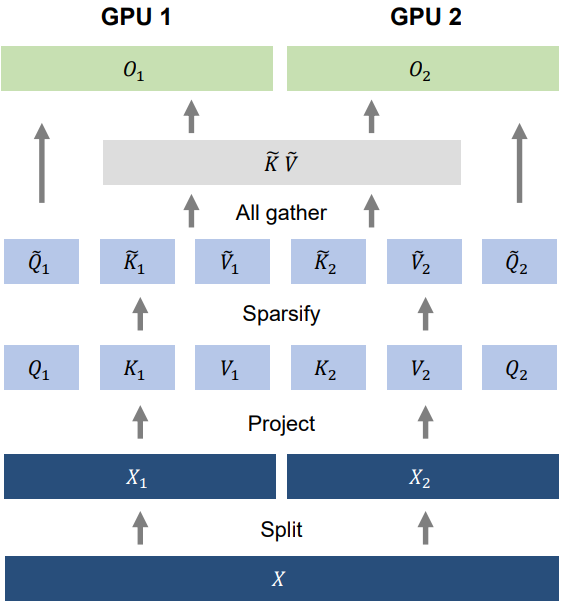
시퀀스 차원의 분산 학습을 위해 LongNet의 선형 계산 복잡도를 활용한다. 위 그림은 일반성을 잃지 않고 두 개의 GPU에 대한 분산 알고리즘을 제시하며 이는 임의의 수의 장치로 추가 확장될 수 있다. 시퀀스 차원을 따라 입력 시퀀스를 분할하는 것부터 시작한다. 각 시퀀스는 하나의 장치에 별도로 배치된다.

\[\begin{equation} X = [X_1, X_2] \end{equation}\]

그런 다음 두 장치의 query, key, value로 project된다.

\[\begin{equation} [Q_1, K_1, V_1] = [W_Q, W_K, W_V] X_1, \quad [Q_2, K_2, V_2] = [W_Q, W_K, W_V] X_2 \end{equation}\]

세그먼트 길이 $w_i \le l$ (여기서 $l$은 로컬 장치의 시퀀스 길이)에 대해 로컬하게 attention 계산한다. 세그먼트 길이 $w_i > l$의 경우 key와 value는 여러 장치에 분산된다. 따라서 attention을 계산하기 전에 key-value 쌍을 수집한다. \(\{Q, K, V\}\)를 \(\{\tilde{Q}, \tilde{K}, \tilde{V}\}\)로 sparsify한다. Key-value 쌍을 수집하기 위해 all-gather 연산이 구현된다.

\[\begin{equation} \tilde{K} = [\tilde{K}_1, \tilde{K}_2], \quad \tilde{V} = [\tilde{V}_1, \tilde{V}_2] \end{equation}\]

역방향의 all-gather 연산은 reduce-scatter 연산이 된다. 바닐라 attention과 달리 \(\tilde{K}_i\)와 \(\tilde{V}_i\)의 크기는 모두 시퀀스 길이 $N$에 독립적이므로 통신 비용이 일정하다.

마지막으로 로컬 query \(\tilde{Q}_i\)와 글로벌 key-value 쌍 ${\tilde{K}, \tilde{V}}$$을 사용하여 cross-attention을 계산한다.

\[\begin{equation} \tilde{O}_1 = \textrm{softmax} (\tilde{Q}_1 \tilde{K}^\top) \tilde{V}, \tilde{O}_2 = \textrm{softmax} (\tilde{Q}_2 \tilde{K}^\top) \tilde{V} \end{equation}\]

여러 장치에 걸쳐 출력을 concat하면 최종 attention 출력이 된다.

\[\begin{equation} \tilde{O} = [\tilde{O}_1, \tilde{O}_2] \end{equation}\]

위에 설명된 분산 알고리즘은 batch 차원을 분할하는 데이터 병렬 처리, hidden 차원을 분할하는 모델 병렬 처리, 레이어를 분할하는 파이프라인 병렬 처리를 비롯한 다른 병렬 처리와 직교한다.

2. Scaling up to 1B Tokens

저자들은 최신 분산 시스템을 통해 10억 토큰으로 확장할 수 있는 가능성을 확인하였다. 8000부터 GPU 메모리 한계까지 시퀀스 길이를 점진적으로 확장한다. Batch당 토큰 수를 10억 개로 유지하기 위해 batch size를 그에 따라 줄인다. 서로 다른 시퀀스 길이의 각 모델에는 최대 3개의 세그먼트 길이, 장치당 토큰 수, 시퀀스 길이가 있다. 저자들은 10개의 서로 다른 run에 대한 forward propagation의 평균 속도를 계산하였다.

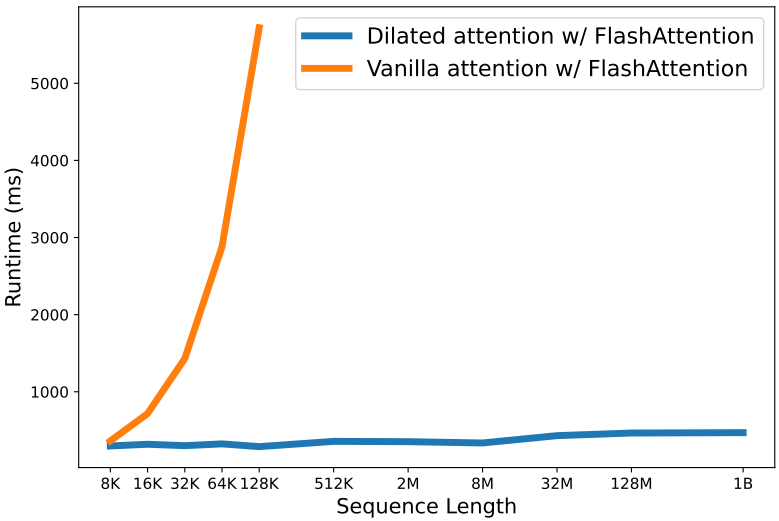
위 그림은 바닐라 attention과 dilated attention의 런타임을 비교한 그래프이다. 둘 다 메모리 절약과 속도 향상을 위해 FlashAttention Kernel로 구현된다. 이는 dilated attention이 거의 일정한 대기 시간으로 시퀀스 길이를 성공적으로 확장할 수 있음을 보여준다. 시퀀스 차원을 분할함으로써 분산 시스템을 활용하여 시퀀스 길이를 10억 개의 토큰으로 확장할 수 있다. 대조적으로, 바닐라 attention은 시퀀스 길이에 대한 2차 의존성으로 인해 어려움을 겪는다. 길이가 길어질수록 대기 시간이 극적으로 늘어난다. 또한 바닐라 attention은 시퀀스 길이 제한을 깨기 위한 분산 알고리즘이 없다. 이는 LongNet의 분산 알고리즘뿐만 아니라 선형 복잡도의 장점도 입증한다.

Experiments on Language Modeling

• 데이터셋: The Stack
  • 프로그래밍 언어 300개의 소스 코드 모음
  • tokenizer: tiktoken (cl100k_base 인코딩)
• 모델 디테일
  • backbone 아키텍처: Magneto (xPos 상대 위치 인코딩 사용)
  • hidden 차원: 768
  • attention head 수: 12
  • 디코더 레이어 수: 12
  • 세그먼트 길이: \(w = \{2048, 4096, 8192, 16384, 32768\}\)
  • dilation rate: \(r = \{1, 2, 4, 6, 12\}\)
• 학습 디테일
  • batch size: 50만 토큰
  • 학습 step 수: 30만

1. Results

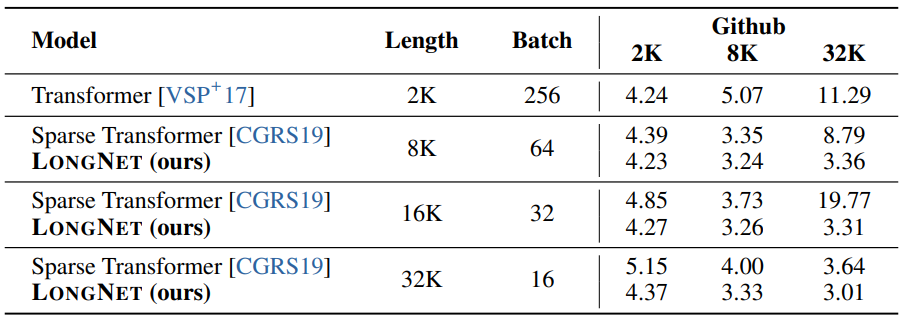
다음은 The Stack에서의 perplexity를 비교한 표이다.

2. Scaling Curves of Sequence Length

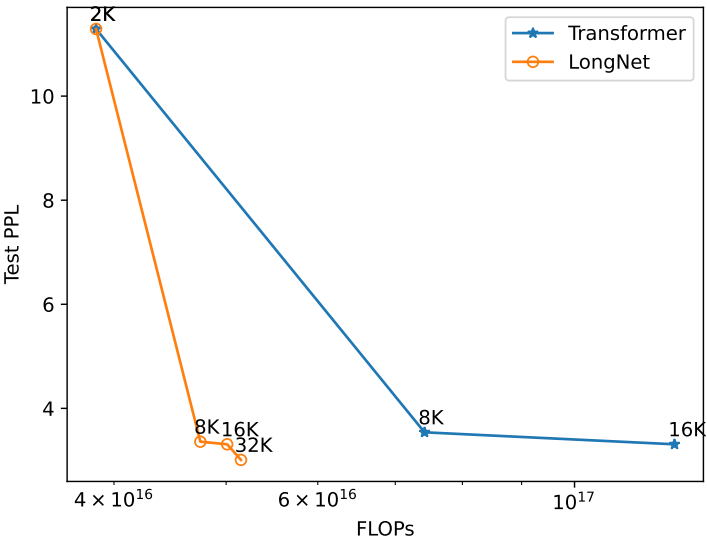
다음은 학습 중에 다양한 시퀀스 길이를 사용하는 LongNet과 dense Transformer의 테스트 perplexity를 비교한 그래프이다.

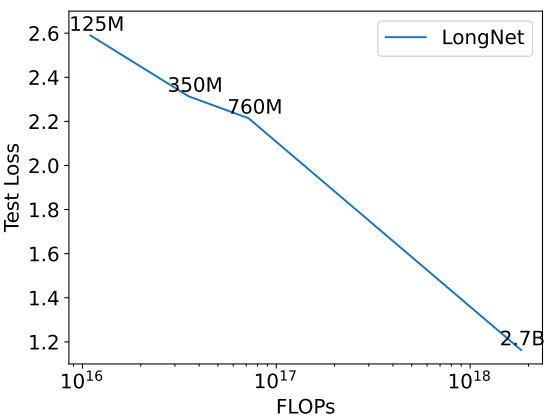
3. Scaling up Model Size

다음은 모델 크기에 따른 test loss를 비교한 그래프이다.

4. Long Context Prompting

다음은 여러 context window에 대한 test loss를 비교한 그래프이다.