[논문리뷰] LODGE: Level-of-Detail Large-Scale Gaussian Splatting with Efficient Rendering

arXiv 2025. [Paper] [Page]
Jonas Kulhanek, Marie-Julie Rakotosaona, Fabian Manhardt, Christina Tsalicoglou, Michael Niemeyer, Torsten Sattler, Songyou Peng, Federico Tombari
Google | CTU in Prague | Google DeepMind
29 May 2025

Introduction

3D Gaussian Splatting (3DGS)의 인기가 높아짐에 따라 이러한 3DGS를 더 크고 복잡한 장면에 적용하는 데 대한 관심이 높아지고 있다. 그러나 표준 방법은 그러한 대규모 환경에 잘 확장되지 않는다. 핵심 문제는 표현에 있다. 미세한 디테일을 캡처하려면 많은 수의 Gaussian이 필요하다. 결과적으로 장면의 먼 영역조차도 최종 렌더링 이미지에 거의 기여하지 않는 세밀한 형상을 나타내는 고밀도 Gaussian으로 채워진다. 이로 인해 최소한의 영향이나 전혀 눈에 띄는 영향이 없음에도 불구하고 많은 멀리 있는 Gaussian이 처리되므로 렌더링 중에 상당한 비효율성이 발생한다. 게다가 메모리 제한은 추가적인 과제를 야기한다. 모든 Gaussian을 동시에 GPU 메모리에 저장할 수 있는 것은 아니며, 특히 메모리가 심각하게 제한된 모바일 기기의 경우 문제가 된다.

컴퓨터 그래픽스에서는 이 문제가 level-of-detail (LOD) 전략을 사용하여 효과적으로 해결되었다. LOD는 게임 내 에셋이 카메라에서 멀리 떨어져 있을 때 저해상도 버전을 렌더링하고 카메라가 가까워지면 점진적으로 고해상도 버전으로 대체한다. 대규모 장면에서 3DGS에 대한 LOD를 제안하는 방법들이 있지만 주로 GPU 메모리에 로드되는 Gaussian 수를 제한하지 않고 렌더링 속도를 개선하는 데 중점을 두어 더 작은 장치에서 렌더링을 어렵게 만든다. 이러한 방법들은 종종 새 프레임마다 렌더링해야 하는 Gaussian들을 다시 계산해야 하므로 렌더링에 오버헤드가 추가된다. 더 중요한 것은 모든 다른 LOD의 모든 Gaussian이 항상 GPU 메모리에 있어야 한다는 것이다. 또한 기존 LOD 접근 방식은 좋은 품질과 성능을 달성하기 위해 각 장면에 대한 신중한 파라미터 조정이 필요하다.

본 논문의 방법은 대규모 장면의 렌더링 속도를 향상시키고 임베디드 기기에서 애플리케이션을 구동하기 위해 메모리에 필요한 Gaussian 수를 제한하도록 설계되었다. 기존의 LOD 기반 방법과 유사하게, 장면을 다양한 LOD를 가진 여러 Gaussian 집합으로 표현한다. 그러나 클러스터 중심을 중심으로 공간에 영역을 정의하는 것을 제안하였다. 각 영역은 미리 계산된 LOD에서 고정된 Gaussian 집합을 활성화하여 서로 다른 프레임 간의 오버헤드 계산을 방지한다.

Method

Preliminaries: Importance pruning

LOD 표현의 일부로 RadSplat에 도입된 importance pruning을 적용한다. 3DGS 학습 중에 많은 Gaussian은 불투명도가 감소하거나 앞에 있는 Gaussian이 불투명해지면 덜 눈에 띄게 된다. 3DGS는 불투명도가 낮은 Gaussian을 주기적으로 제거하지만, 가려진 Gaussian은 제거하지 않는다. RadSplat은 모든 학습 카메라의 모든 픽셀에 대한 Gaussian의 기여도에서 최대값을 취하여 각 Gaussian의 중요도 점수를 측정하는 것을 제안하였다. 중요도 점수가 특정 threshold보다 낮은 모든 Gaussian을 제거함으로써 렌더링에 거의 영향을 미치지 않고 Gaussian을 효과적으로 pruning할 수 있다. 이렇게 하면 렌더링이 더 빨라지고 메모리도 줄어든다. 학습 중에 RadSplat을 따라 두 번 pruning한다.

Level of Detail (LOD) representation

3D 장면을 다양한 LOD에 대응하는 여러 Gaussian 집합으로 표현한다. 장면의 원거리 영역은 최종 렌더링에 거의 기여하지 않는 많은 Gaussian으로 표현되는 경우가 많다. 그러나 이러한 Gaussian은 렌더러에서 여전히 계산되어야 하므로 과도한 메모리 사용 및 계산이 발생한다. 보이는 Gaussian이 많은 픽셀은 픽셀이 16$\times$16 패치들로 처리되는 방식으로 인해 렌더링 속도를 크게 저하시킬 수 있다. 따라서 주요 목표는 보이는 Gaussian이 많은 픽셀의 수를 줄이는 것이다.

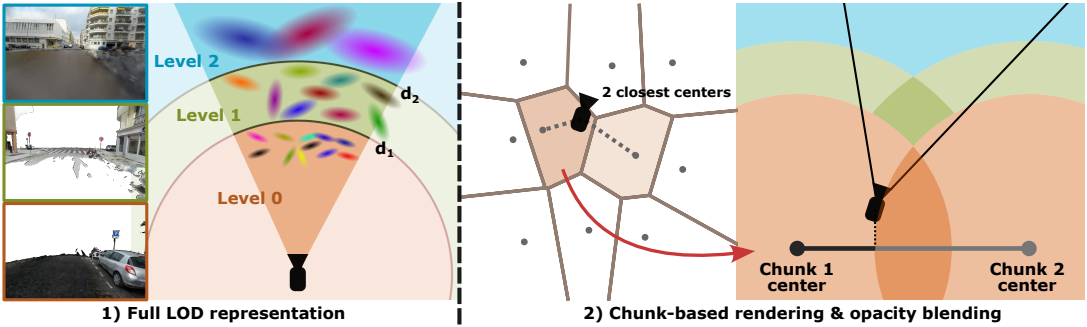
따라서 덜 자세한 Gaussian 집합으로 먼 영역을 표현하고 더 자세한 집합으로 가까운 영역을 표현한다. 이를 위해 여러 LOD 레벨 $\mathcal{G}^{(l)}$을 정의한다 ($0 < l < L$). 여기서 $\mathcal{G}^{(0)}$는 원본 이미지 집합에서 최적화하여 얻은 가장 자세한 Gaussian 집합을 나타낸다. 각 LOD 레벨 $\mathcal{G}^{(l)}$은 최소 $d_l$의 거리에서 관찰할 때 충분한 렌더링 품질이 달성되도록 구성된다고 가정한다. 주어진 카메라 포즈에서 LOD를 렌더링할 때 각 LOD 레벨에서 Gaussian의 부분 집합을 선택한다. 이 집합을 active Gaussian이라고 하며, 카메라 중심 $\textbf{c}$에 대해 다음과 같이 정의된다.

\[\begin{equation} \tilde{\mathcal{G}} (\textbf{c}) = \bigcup_{l=0}^{L-1} \left\{ g_i \in \mathcal{G}^{(l)} \, : \, d_l \le \| \mu_i^{(l)} - \textbf{c} \|_2 < d_{l+1} \right\} \\ \textrm{where} \quad d_0 = 0, \; d_L = \infty \end{equation}\]

($\mu_i^{(l)}$은 레벨 $l$의 Gaussian $g_i$의 평균)

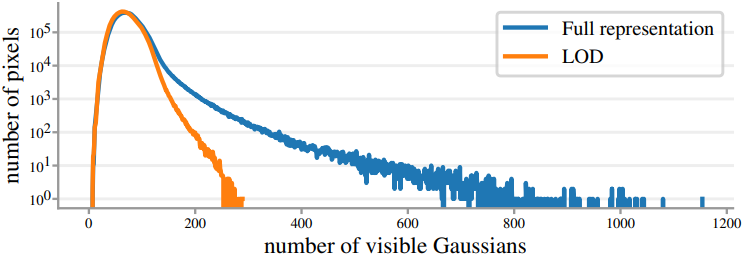
아래 그림에서 볼 수 있듯이, LOD 렌더링은 픽셀당 보이는 Gaussian의 분포의 긴 꼬리를 줄여 렌더링 속도를 높인다.

Building LOD representation

적어도 $d_l$의 거리에서 관찰했을 때 충분한 렌더링 품질이 달성되도록 각 LOD 레벨 $\mathcal{G}^{(l)}$을 구성해야 한다. 저자들은 Mip-Splatting에서 제안한 3D 필터에서 영감을 얻었다. 렌더링된 이미지는 Gaussian 집합으로 주어진 연속 3D 장면의 2D projection인 반면, 이미지 자체는 대신 각 픽셀 좌표가 연속 3D 신호의 샘플링을 정의하는 그리드이다. 초점 거리가 $f$일 때, screen space에서 샘플링 간격이 1인 경우 깊이 $d$에서 3D world space의 픽셀 간격은 $T = \frac{d}{f}$이다.

Nyquist’s theorem에 따르면 신호의 성분은 $2T$보다 작은 간격으로 샘플링된 경우에만 재구성할 수 있다. 따라서 $2T$보다 작은 Gaussian은 앨리어싱 아티팩트만 발생하고 메모리 사용량과 렌더링 시간이 모두 늘어난다. Gaussian이 $2T$보다 크기가 커지도록 강제하기 위해, Mip-Splatting을 따라 각 Gaussian을 smoothing 3D filter로 convolution한다. 평균이 $\mu$이고 공분산이 $\Sigma$인 Gaussian과 깊이 $d$에 대한 Gaussian 함수는 다음과 같다.

\[\begin{equation} \tilde{G} (\textbf{x}) = \sqrt{\frac{\vert \Sigma \vert}{\vert \Sigma + \frac{sd}{f} \cdot \textbf{I} \vert}} \exp \left(-\frac{1}{2} (\textbf{x} - \mu)^\top (\Sigma + \frac{sd}{f} \cdot \textbf{I})^{-1} (\textbf{x} - \mu) \right) \end{equation}\]

($s$는 hyperparameter)

$d_l$보다 큰 거리에서 보이는 낮은 디테일의 표현 $\mathcal{G}^{(l)}$을 구축하기 위해 $\mathcal{G}^{(0)}$에서 Gaussian을 복사하고 깊이 $d_l$에 대한 smoothing 3D filter를 적용한다. 이 3D 필터만 적용한다고 해서 Gaussian이 직접적으로 줄어드는 것은 아니지만, 상당수의 Gaussian이 중복되어 알파 블렌딩에서의 기여도가 감소한다. 따라서, RadSplat의 중요도 점수를 사용하여 사용하지 않는 Gaussian을 반복적으로 제거한다. Gaussian 제거로 인해 발생하는 오차를 수정하기 위해 몇 번의 fine-tuning step을 사용한다. Fine-tuning의 경우, 최적화된 LOD 레벨까지 레벨을 사용하여 LOD 렌더링을 사용한다.

Selecting depth thresholds

렌더링 성능을 극대화하기 위해 깊이 threshold $d_l$을 어떻게 선택해야 할까? 렌더러는 16$\times$16 타일로 그룹화된 픽셀에서 작동하며 렌더링 성능은 동일한 16$\times$16픽셀 타일 내부에서 처리되는 Gaussian 수에 크게 영향을 받는다. 타일 내의 모든 스레드가 모든 보이는 Gaussian의 합집합을 처리하고 가장 느린 스레드가 rasterization을 완료할 때까지 기다려야 하기 때문이다. 처리되는 Gaussian 수에 대한 임계값의 영향을 이론적으로 분석하는 것은 어렵지만, 학습 뷰의 부분 집합을 렌더링하여 다양한 threshold에 대한 이 수를 추정하고 타일당 평균 Gaussian 수를 최소화하는 threshold를 선택할 수 있다.

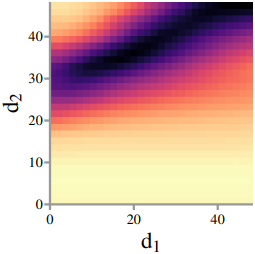
위 그림은 깊이 $d_1$과 $d_2$의 두 LOD 레벨에 대한 비용 분포를 보여준다. 최소값의 값이 \(\{(x, ax+b) : x \in \mathbb{R}\}\)과 유사하다. 이를 이용하여, $d_1$에서 시작하여 반복적으로 threshold를 추가하는 greedy 전략을 활용할 수 있다. 이를 통해 탐색 문제의 복잡도를 선형적인 복잡도로 줄일 수 있다.

Reducing memory with chunk-based rendering

지금까지 설명한 LOD 렌더링은 보이는 Gaussian의 수를 줄여 rasterization 속도를 높이지만, 모든 Gaussian은 여전히 GPU 메모리에 로드되어야 한다. 또한, active Gaussian은 지속적으로 재계산되어야 하므로 오버헤드 계산이 발생한다.

이 문제를 해결하기 위해, 본 논문에서는 장면을 청크라고 불리는 여러 영역으로 분할하고 청크당 고정된 active Gaussian 집합을 저장하는 방안을 제안하였다. 이미지를 렌더링할 때, rasterizer는 가장 가까운 청크에 대해 미리 계산된 active Gaussian을 사용한다. 학습 카메라 위치에 대해 K-means clustering을 수행하여 장면을 청크로 분할한다. 각 청크에 대해, 카메라 위치 대신 청크 중심 $\textbf{c}$를 대해 active Gaussian이 계산되며, 청크 반경(가장 가까운 청크 중심까지의 거리)을 깊이 $d_l$을 사용하여 청크 내부의 모든 카메라 위치에 충분한 해상도를 보장한다.

Visibility filtering

LOD 청크를 고려하여 각 LOD 청크에 대한 Gaussian 집합을 필터링하여 렌더링 속도를 더욱 높인다. 각 LOD 청크에 대해 importance pruning을 추가로 수행한다. 즉, Gaussian별 중요도 점수를 계산하고 고정 threshold보다 낮은 중요도 점수를 가진 모든 Gaussian을 제거한다. Robustness를 더욱 높이기 위해, LOD 청크 내 기존 학습 뷰에 랜덤한 perturbation을 추가하여 뷰를 추가한다. 구체적으로, 원래 카메라 위치를 사용하고 방향을 랜덤 샘플링한다.

Opacity blending for smooth cross-chunk transitions

이러한 청크를 구성한 후, 청크 중심에 대한 active Gaussian을 단순히 렌더링하면 렌더링 속도를 높이고 메모리를 절약하지만, 카메라 궤적의 동적 동영상을 렌더링할 때 급격한 변화를 초래한다. 이러한 아티팩트는 본질적으로 전환 중에 어떠한 형태의 smoothing 필터도 사용하지 않고 이동하는 동안 active Gaussian의 급격한 변화로 인해 발생한다.

저자들은 이 문제를 해결하기 위해, 가장 가까운 두 청크를 활용하는 smoothing 전략을 제안하였다. 이미지를 렌더링할 때 먼저 가장 가까운 두 청크 중심을 찾는다. 각각의 active Gaussian 집합을 가져와 결합한다. 그런 다음, 두 active Gaussian 집합의 교집합에 없는 Gaussian의 불투명도를 다음과 같이 변조한다.

\[\begin{equation} \hat{\alpha}_i = \alpha_i t, \quad t = \textrm{min}(1, \textrm{max}(0, \bar{t})), \quad \bar{t} = \frac{(\textbf{c} - \textbf{m}_o)^\top (\textbf{m}_f - \textbf{m}_o)}{\| \textbf{m}_o - \textbf{m}_f \|_2^2} \end{equation}\]

($\textbf{c}$는 현재 카메라 위치, \(\textbf{m}_f\)는 Gaussian $i$가 속하는 청크의 중심, \(\textbf{m}_o\)는 Gaussian $i$를 포함하지 않는 다른 청크의 중심)

카메라가 청크 중심을 통과하지 않더라도 부드러운 전환을 얻기 위해 유클리드 거리 대신 projection의 길이 $\bar{t}$를 사용한다. 불투명도가 수정된 두 active Gaussian 집합의 합집합이 주어지면 표준 rasterization 단계를 진행한다. 두 청크의 합집합만 메모리에 로드해야 하며, 각 렌더링 pass에서 두 active Gaussian 집합의 차집합의 불투명도만 업데이트하면 된다. 실제로 LOD 분할을 다시 로드하는 것은 렌더러의 런타임에 영향을 미치지 않는 백그라운드 프로세스에서 수행될 수 있다.

Experiments

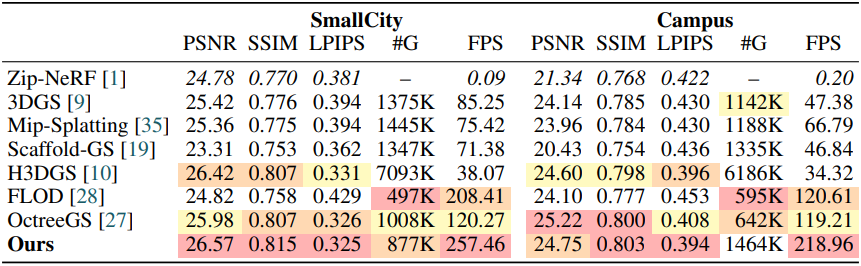
다음은 SmallCity와 Campus 장면에서의 비교 결과이다.

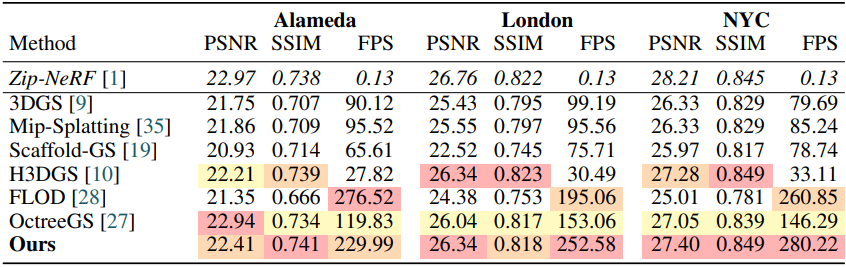
다음은 Zip-NeRF 데이터셋에서의 비교 결과이다.

다음은 다양한 설정에 대한 성능 분석 결과이다.

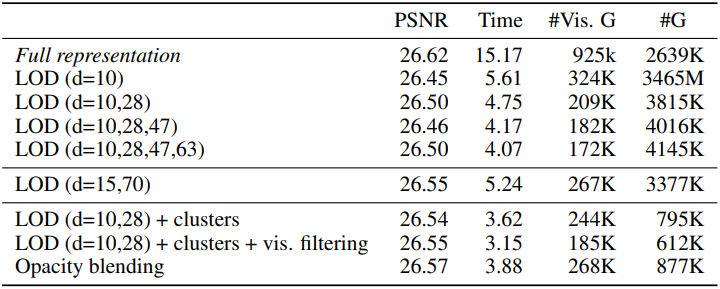
다음은 ablation study 결과이다.

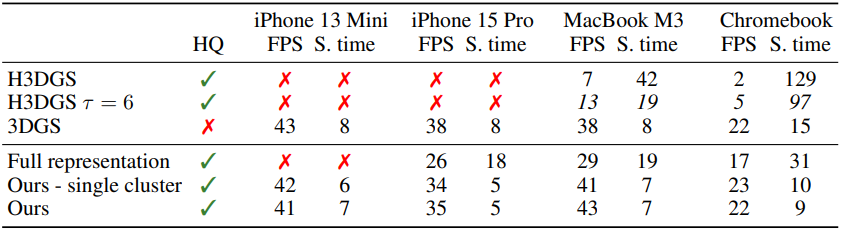
다음은 모바일 기기에서의 렌더링 FPS와 정렬 시간(ms)을 비교한 결과이다.