Diffusion은 신이고 GPT는 무적이다

CVPR 2024 (Highlight). [Paper] [Page] [Github]
Rinon Gal, Yael Vinker, Yuval Alaluf, Amit H. Bermano, Daniel Cohen-Or, Ariel Shamir, Gal Chechik
Tel Aviv University | NVIDIA | Reichman University
21 Nov 2023


Introduction

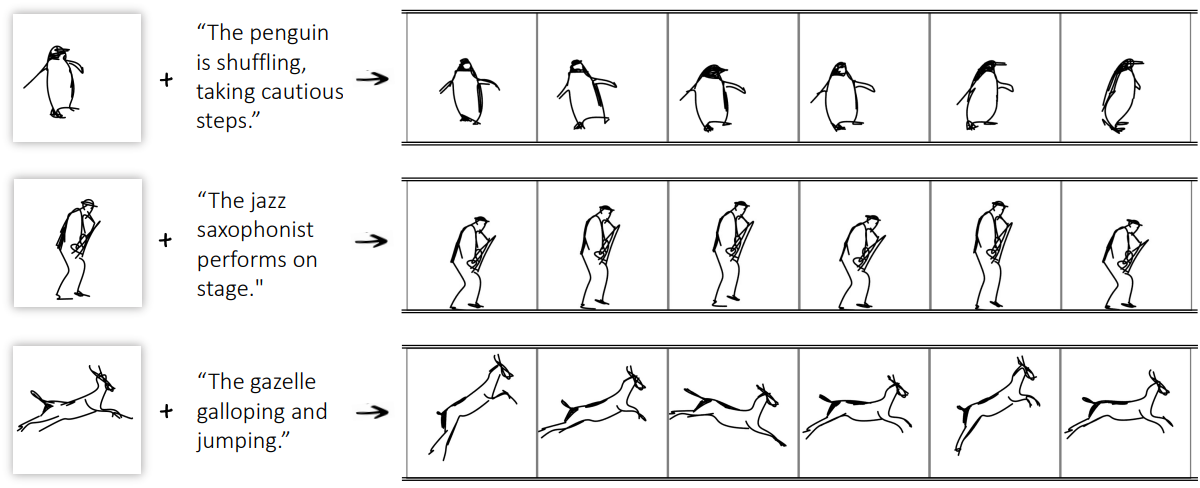
본 논문에서는 인간의 주석이나 명시적 참조 모션 없이 텍스트 프롬프트를 기반으로 주어진 정적 스케치에 생명을 불어넣는 것을 제안하였다. 사전 학습된 text-to-video (T2V) diffusion model을 활용하여 이를 수행한다. 최근의 여러 연구에서는 diffusion model의 prior를 사용하여 정적 이미지에 생명을 불어넣는 것을 제안하였다. 그러나 스케치는 이 도메인을 염두에 두고 설계되지 않았기 때문에 기존 방법에서는 해결하지 못하는 고유한 과제를 제기한다. 본 논문의 방법은 T2V 모델의 최근 발전을 이 새로운 도메인으로 가져와 스케치 애니메이션의 어려운 과제를 해결하는 것을 목표로 한다. 이를 위해 이 추상적 도메인의 섬세한 특성을 고려한 구체적인 디자인 선택을 제안하였다.

이전 스케치 생성 방법과 마찬가지로 스케치의 벡터 표현을 사용하여 스케치를 스트로크 (Bezier curve)의 집합으로 정의하였으며, 이는 control point들로 parameterize되었다. 벡터 표현은 해상도에 독립적이므로 품질을 손상시키지 않고 크기를 조정할 수 있다. 게다가 쉽게 편집할 수 있다. 다른 스트로크 스타일을 선택하여 스케치의 모양을 수정하거나 control point들을 끌어서 모양을 변경할 수 있다. 또한 sparsity 덕분에 pixelization과 blurring을 방지하면서 부드러운 모션을 촉진한다.

정적 스케치에 생명을 불어넣기 위해, 주어진 텍스트 프롬프트에 따라 각 동영상 프레임의 스트로크 파라미터를 수정하도록 네트워크를 학습시킨다. 본 논문의 방법은 최적화 기반이며, 대규모 모델의 데이터나 fine-tuning이 필요하지 않다. 또한, 일반적이며 다양한 T2V 모델에 쉽게 적용할 수 있다.

저자들은 score distillation sampling (SDS) loss를 사용하여 네트워크를 학습시켰다. 이 loss는 픽셀이 아닌 표현 (ex. NeRF, SVG)을 최적화하여 주어진 텍스트 기반 제약 조건을 충족하기 위해 사전 학습된 text-to-image (T2I) diffusion model을 활용하도록 설계되었다. 이 loss를 사용하여 사전 학습된 T2V diffusion model에서 motion prior들을 추출한다. 이를 통해 diffusion model에 내장된 인터넷 스케일의 지식을 상속하여 여러 카테고리에 걸쳐 광범위한 주제에 대한 애니메이션을 구현할 수 있다.

저자들은 물체의 움직임을 두 가지 구성 요소, 즉 로컬 모션과 글로벌 모션으로 분리하였다. 로컬 모션은 고립된 로컬 효과를 포착하는 것을 목표로 한다. 반대로 글로벌 모션은 모양 전체에 영향을 미치며 프레임별 변환 행렬을 통해 모델링된다. 따라서 고정된 모션을 포착하거나, 효과를 조정할 수 있다. 이러한 분리는 원래 피사체의 특성에 충실하면서도 로컬하게 부드럽고 글로벌하게 의미있는 모션을 생성하는 데 중요하다.

Method

  • 입력
    • 벡터 형식의 정적 스케치
    • 원하는 모션을 설명하는 텍스트 프롬프트
  • 출력
    • 스케치가 프롬프트와 일치하는 방식으로 행동하는 벡터 형식의 짧은 동영상
  • 목표
    1. 출력 동영상은 텍스트 프롬프트와 일치해야 한다.
    2. 원본 스케치의 특성이 보존되어야 한다.
    3. 생성된 모션은 자연스럽고 매끄럽게 보여야 한다.

1. Representation


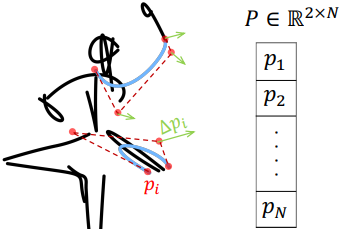
입력 벡터 이미지는 흰색 배경 위에 배치된 일련의 스트로크로 표현되며, 각 스트로크는 4개의 control point가 있는 2차원 Bezier curve이다. 각 control point는 좌표로 표현된다: $p = (x, y) \in \mathbb{R}^2$. 단일 프레임의 control point 집합을 \(P = \{p_1, \ldots, p_N\} \in \mathbb{R}^{N \times 2}\)로 표시한다. 여기서 $N$은 입력 스케치의 총 control point의 개수이며, 생성된 모든 프레임에서 고정된다. $k$개의 프레임이 있는 동영상을 $k$개의 이러한 control point 집합의 시퀀스로 정의하고 \(Z = \{P^j\}_{j=1}^k \in \mathbb{R}^{N \cdot k \times 2}\)로 표시한다.

$P^\textrm{init}$을 초기 스케치의 control point 집합이라 하자. $P^\textrm{init}$을 $k$번 복제하여 초기 프레임 집합 $Z^\textrm{init}$을 만든다. 목표는 이러한 정적 프레임 시퀀스를 텍스트 프롬프트에 설명된 모션에 따라 피사체를 애니메이션화하는 프레임 시퀀스로 변환하는 것이다. 이 task는 2D 변위 집합 \(\Delta Z = \{\Delta p_i^j\}_{i \in N}^{j \in k}\)을 학습하는 것으로 볼 수 있다. ($\Delta p_i^j$는 각 프레임 $j$에 대한 각 control point $p_i^j$의 변위)

2. Text-Driven Optimization


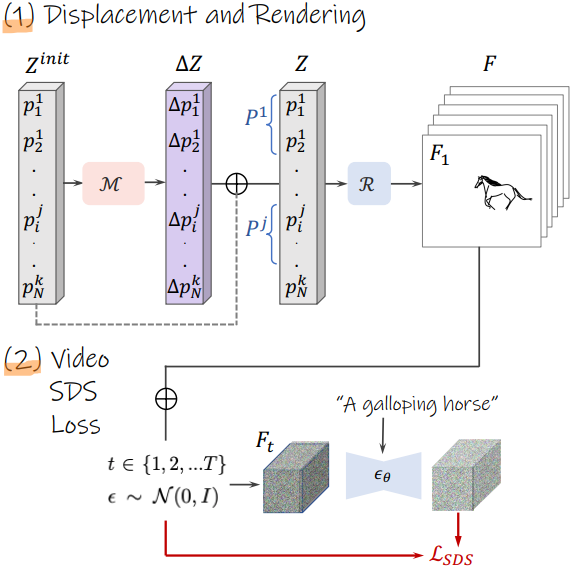
첫 번째 목표인 텍스트 프롬프트와 일치하는 출력 애니메이션을 만드는 것으로 시작하자. 저자들은 “neural displacement field”를 사용하여 애니메이션을 모델링하였다. 이것은 초기 포인트 세트 $Z^\textrm{init}$을 입력으로 받고 변위 $\mathcal{M}(Z^\textrm{init}) = \Delta Z$를 예측하는 작은 네트워크 $\mathcal{M}$이다. 이 네트워크를 학습시키기 위해 SDS loss를 사용하여 사전 학습된 T2V diffusion model에 포함되어 있는 motion prior를 distillation한다.

\[\begin{equation} \nabla_\phi \mathcal{L}_\textrm{SDS} = \bigg[ w(t) (\epsilon_\theta (x_t, t, y) - \epsilon) \frac{\partial x}{\partial \phi} \bigg] \end{equation}\]

각 학습 iteration에서 예측된 변위 벡터 $\Delta Z$를 $Z^\textrm{init}$에 추가하여 시퀀스 $Z$를 형성한다. 그런 다음 미분 가능한 rasterizer $\mathcal{R}$을 사용하여 각 프레임별 점 집합 $P^j$를 픽셀 공간의 해당 프레임 $F^j = \mathcal{R}(P^j)$로 전송한다. 애니메이션 스케치는 rasterization된 프레임들을 concat한 것으로 정의된다.

\[\begin{equation} F = \{F^1, \ldots, F^k\} \in \mathbb{R}^{h \times w \times k} \end{equation}\]

다음으로, diffusion timestep $t$와 noise $\epsilon \sim \mathcal{N}(0, I)$을 샘플링한다. 이를 사용하여 rasterization된 동영상에 noise를 추가하여 $F_t$를 생성한다. $F_t$는 사전 학습된 T2V diffusion model $\epsilon_\theta$를 사용하여 noise가 제거된다. 여기서 diffusion model은 애니메이션 장면을 설명하는 프롬프트에 따라 컨디셔닝된다. 마지막으로, SDS loss를 사용하여 $\mathcal{M}$의 파라미터를 업데이트하고 프로세스를 반복한다.

따라서 SDS loss는 $\mathcal{M}$이 원하는 텍스트 프롬프트와 일치하는 애니메이션을 가진 변위를 학습하도록 가이드한다. 이 정렬의 범위와 그에 따른 모션의 강도는 diffusion guidance scale과 learning rate와 같은 최적화 hyperparameter에 의해 결정된다. 그러나 hyperparameter를 늘리면 일반적으로 아티팩트가 발생하여 원래 스케치의 충실도와 자연스러운 모션의 유동성이 모두 손상된다. 따라서 SDS만으로는 입력 스케치 특성을 보존하고 자연스러운 모션을 만드는 데 실패한다. 대신 displacement field $\mathcal{M}$의 설계를 통해 이러한 목표를 해결한다.

3. Neural Displacement Field

저자들은 모양 변형을 줄여 더 부드러운 모션을 생성하려는 의도로 네트워크 설계에 접근하였다. 저자들은 제약 없는 SDS 최적화 접근 방식에서 관찰된 아티팩트가 부분적으로 두 가지 메커니즘에 기인할 수 있다고 가정하였다.

  1. 생성된 모양을 T2V 모델의 semantic prior와 더 잘 일치하는 모양으로 변형하여 SDS loss를 최소화할 수 있다.
  2. 부드러운 모션에는 로컬 스케일에서 작은 변위가 필요하고, 네트워크는 이를 글로벌 변환에 필요한 큰 변화와 조정하는 데 어려움을 겪는다.

저자들은 두 가지 구성 요소를 통해 모션을 모델링하여 이러한 두 가지 과제를 모두 해결한다.

  1. Local path: 제약 없이 작은 변형을 모델링
  2. Global path: 전체 프레임에 균일하게 적용되는 affine transformation들을 모델링

이 분할을 통해 네트워크는 semantic의 변화를 제한하는 동시에 두 스케일에 따라 모션을 별도로 모델링할 수 있다.

공유 backbone


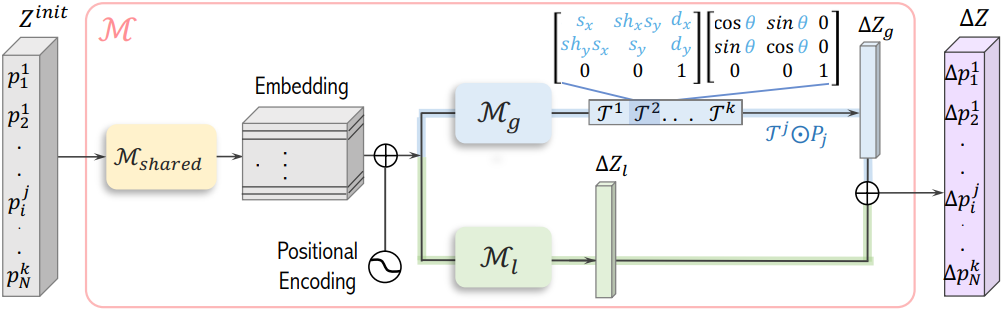
네트워크는 초기 control point 집합 Z^\textrm{init}을 프레임당 변위 $\mathcal{M}(Z^\textrm{init}) = \Delta Z$에 매핑하는 것을 목표로 한다. 먼저, $Z^\textrm{init}$은 local path와 global path에 공급할 공유 feature를 만드는 공유 backbone을 통과한다. 구체적으로, 각 control point의 좌표는 공유 행렬 \(\mathcal{M}_\textrm{shared}\)를 사용하여 projection된 다음 프레임 인덱스와 스케치의 점 순서에 따라 달라지는 위치 인코딩과 합산된다.

Local path

Local path는 공유 feature를 가져와 $Z^\textrm{init}$의 모든 control point에 대한 offset $\Delta Z_l$에 매핑하는 작은 MLP인 \(\mathcal{M}_l\)이다. 여기서 목표는 네트워크가 주어진 프롬프트와 가장 잘 일치하도록 제약 없는 모션을 스스로 학습하도록 하는 것이다. 반면, 이 경로를 사용하여 글로벌한 변경에 필요한 스케일의 변위를 생성하려면 더 강력한 SDS guidance 또는 더 큰 learning rate가 필요하여 원치 않는 변형이 발생한다. 따라서 이러한 변경을 global path에 위임한다.

Global path

Global path의 목표는 모델이 물체의 원래 모양을 유지하면서 질량 중심 이동, 회전, 크기 조정과 같은 글로벌한 이동을 캡처할 수 있도록 하는 것이다. 이 경로는 각 프레임 $P^j$에 대해 하나의 글로벌한 transformation matrix $\mathcal{T}^j$를 예측하는 신경망 \(\mathcal{M}_g\)로 구성된다. 그런 다음 행렬을 사용하여 해당 프레임의 모든 control point를 변환하여 모양이 일관되도록 한다.

구체적으로, 글로벌 모션을 scaling, shear, rotation, translation의 순차적 적용으로 모델링한다. 이는 표준 affine matrix 형식을 사용하여 다음과 같이 parameterize된다.

\[\begin{equation} \mathcal{T}^j = \begin{bmatrix} s_x & sh_x s_y & d_x \\ sh_y s_x & s_y & d_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \end{equation}\]

(scaling: $s_x$, $s_y$ / shear: $sh_x$, $sh_y$ / rotation: $\theta$ / translation: $d_x$, $d_y$)

프레임 $j$의 각 점에 대한 글로벌 변위는 다음과 같다.

\[\begin{equation} \Delta p_{i, \textrm{global}}^j = \mathcal{T}^j \odot p_i^\textrm{init} - p_i^\textrm{init} \end{equation}\]

생성된 모션의 개별 구성 요소에 대한 사용자 제어를 더욱 확장하기 위해 각 유형의 변환에 대해 스케일링 파라미터를 추가한다. 각각 translation, rotation, scale, shear에 대해 \(\lambda_t\), \(\lambda_r\), \(\lambda_s\), \(\lambda_{sh}\)이다.

예를 들어, $(d_x^j, d_y^j)$가 네트워크의 예측된 translation 파라미터라고 하면, 다음과 같이 크기를 조정한다.

\[\begin{equation} (d_x^j, d_y^j) \rightarrow (\lambda_t d_x^j, \lambda_t d_y^j) \end{equation}\]

이를 통해 원치 않는 모션의 특정 측면을 약화할 수 있다. 예를 들어, $\lambda_t = 0$으로 설정하여 피사체를 대략 고정 상태로 유지할 수 있다. 제한된 변환을 통해 글로벌한 변경을 모델링하고 전체 프레임에 균일하게 적용함으로써 큰 ​효과를 생성하는 능력을 유지하면서도 임의의 변형을 생성하는 모델의 능력을 제한한다.

최종적으로 예측된 ​​변위 $\Delta Z$는 단순히 두 path의 출력을 합한 것이다.

\[\begin{equation} \Delta Z = \Delta Z_l + \Delta Z_g \end{equation}\]

이 두 항의 강도는 각 path를 최적화하는 데 사용된 learning rate와 guidance scale에 의해 결정되며, 첫 번째 목표 (텍스트와 일치하는 동영상)와 나머지 두 목표 (원래 스케치의 모양을 보존하고 부드럽고 자연스러운 모션을 생성) 간의 trade-off에 영향을 미친다. 따라서 사용자는 이 trade-off를 사용하여 생성된 동영상에 대한 추가 제어를 얻을 수 있다. 예를 들어, local path에 대해 낮은 learning rate를 사용하여 스케치 모양의 보존을 우선시하면서 글로벌 모션에 더 큰 자유도를 제공할 수 있다.

Experiments

  • 학습 디테일
    • diffusion backbone: ModelScope text-to-video
    • optimizer: Adam
    • learning rate
      • local path: $1 \times 10^{-4}$
      • global path: $5 \times 10^{-3}$
    • step: 1,000
    • 동영상 1개를 생성하는 데 A100 GPU 1개에서 30분 소요
    • augmentation: random crop, perspective transformation
    • \(\lambda_t = 1.0\), \(\lambda_r = 0.01\), \(\lambda_s = 0.05\), \(\lambda_{sh} = 0.1\)

다음은 주어진 스케치를 주어진 프롬프트로 애니메이션화하는 예시들이다.


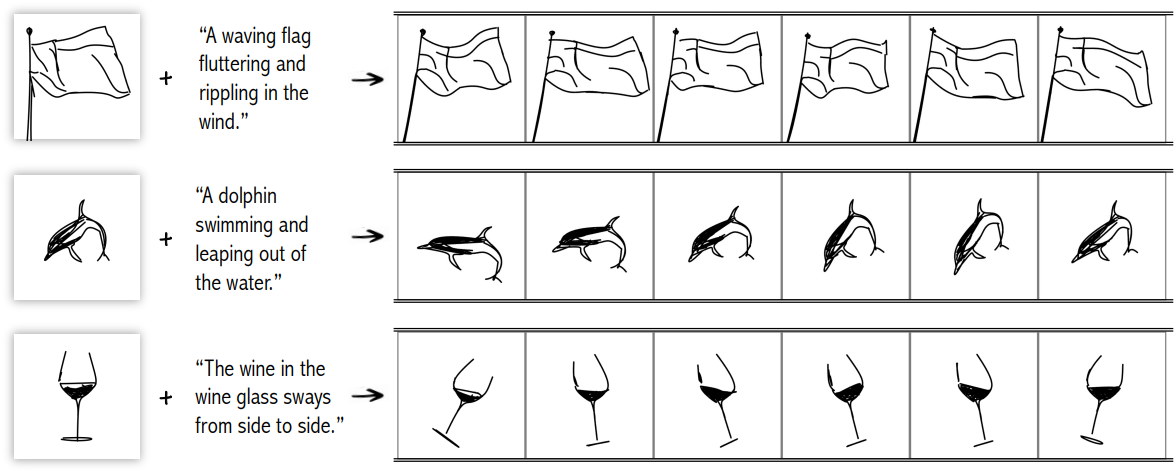
다음은 동일한 스케치에 서로 다른 프롬프트를 적용한 예시이다.

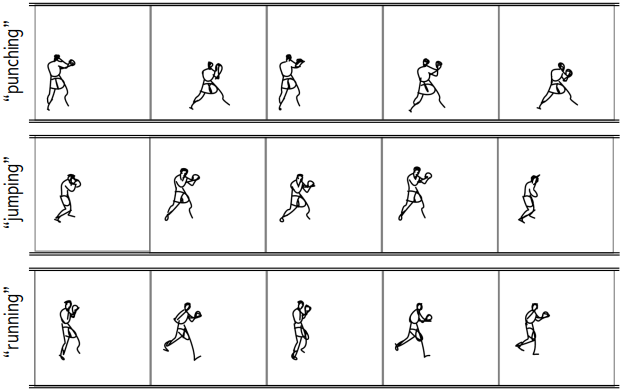
1. Comparisons

다음은 다른 방법들과 비교한 결과이다.

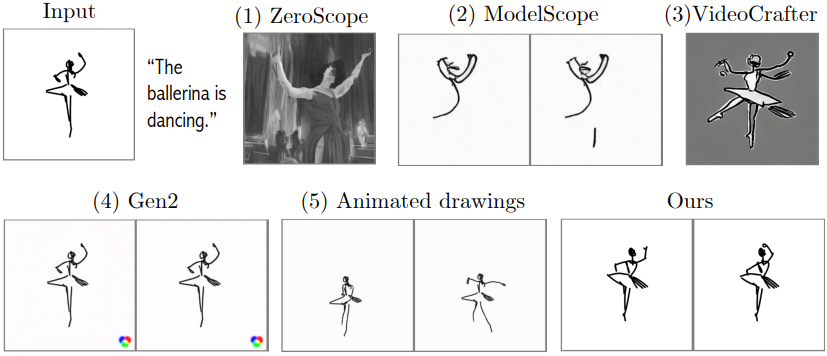
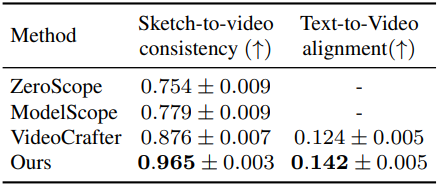
2. Ablation Study

다음은 ablation 결과이다.


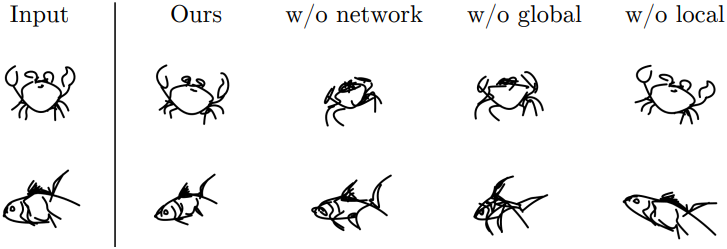
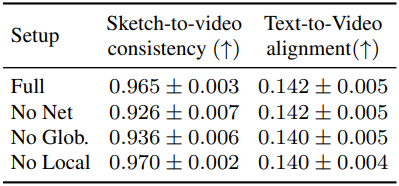
다음은 ablation에 대한 user study 결과이다.

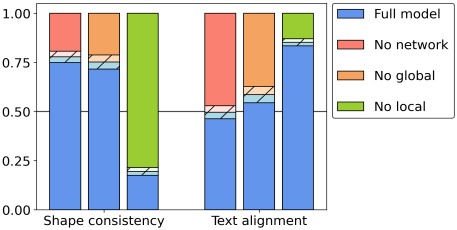
Limitations


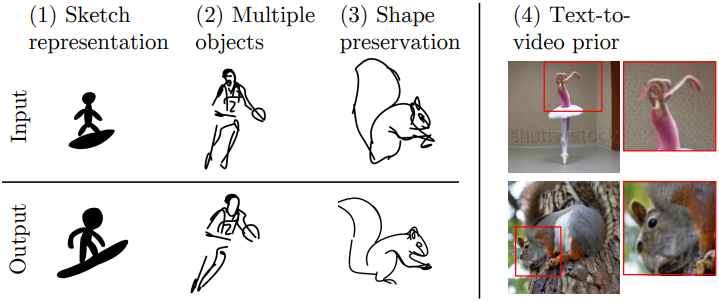
  1. 다른 스케치 표현과 함께 사용하면 성능이 저하될 수 있다.
  2. 입력 스케치가 하나의 피사체를 표현하고 있다고 가정하고 있다.
  3. 모션 품질과 스케치 충실도 사이에서 trade-off를 맞춰야 한다.
  4. T2V prior의 한계를 물려받기 때문에 특정 모션을 인식하지 못하거나 강한 편향을 나타낼 수 있다.

You may also enjoy