[논문리뷰] Generating Physically Stable and Buildable LEGO Designs from Text
ICCV 2025 (Oral). [Paper] [Page] [Github] [Demo]
Ava Pun, Kangle Deng, Ruixuan Liu, Deva Ramanan, Changliu Liu, Jun-Yan Zhu
Carnegie Mellon University
8 May 2025
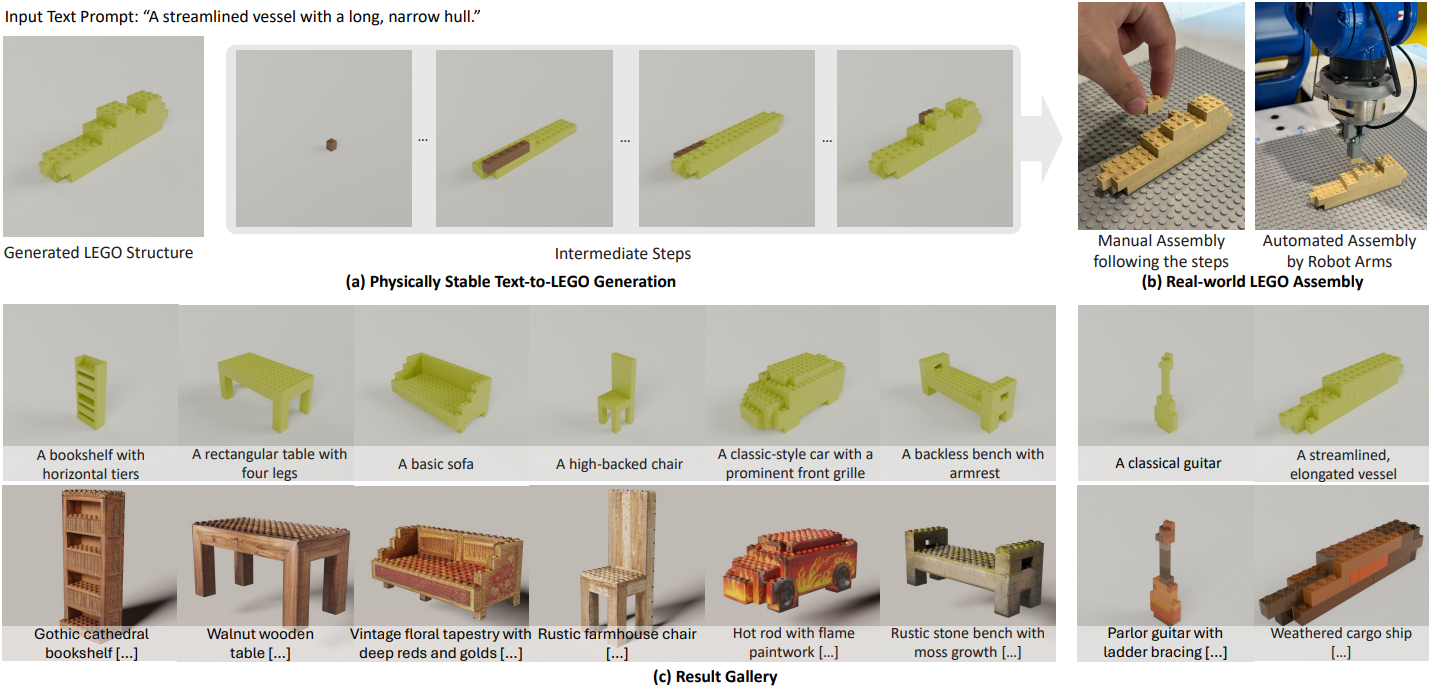
Introduction
기존 방법들로 실제 물체를 만드는 것은 여전히 어려운 일이다. 대부분의 방법들은 고충실도의 형상과 외관을 가진 다양한 3D 물체를 생성하는 데 중점을 두지만, 이러한 디지털 디자인은 두 가지 주요 문제로 인해 물리적으로 구현하기 어려운 경우가 많다.
- 표준 부품을 사용하여 물체를 조립하거나 제작하기 어려울 수 있다.
- 조립이 가능하더라도 최종 구조가 물리적으로 불안정할 수 있다. 설계의 일부가 무너지거나, 떠다니거나, 분리된 상태로 남을 수 있다.
본 논문에서는 물리적으로 구현 가능한 물체를 생성하는 과제를 다루고, 이 문제를 LEGO 디자인의 맥락에서 연구하였다. LEGO는 모든 구성 요소를 쉽게 구할 수 있으므로 재현 가능한 연구 벤치마크로 활용할 수 있다.
본 논문의 목표는 물리적 안정성과 조립 가능성을 보장하면서 텍스트 프롬프트에서 직접 LEGO 디자인을 생성하는 생성 모델을 학습시키는 것이다.
- 물리적 안정성: 브릭이 뜨거나 무너지지 않고 견고한 구조적 무결성을 갖춘 LEGO 베이스플레이트 위에 제작된다.
- 조립 가능성: 일반 LEGO 조각과 호환되며 사람이나 로봇이 브릭을 하나씩 조립할 수 있다.
본 논문에서는 원래 next-token prediction을 위해 학습된 LLM을 next-brick prediction을 위해 재활용하는 LeogGPT를 소개한다. LEGO 디자인 문제를 autoregressive한 텍스트 생성 task로 공식화하며, 여기서 다음 브릭의 크기와 위치는 간단한 텍스트 형식으로 지정된다. 생성된 구조가 안정적이고 조립 가능하도록 하기 위해 학습 및 inference 과정에서 물리 기반 조립 제약 조건을 적용하였다. 저자들은 캡션과 함께 물리적으로 안정적인 LEGO 디자인의 대규모 데이터셋을 구성하였다. 또한, inference 시에 효율적인 유효성 검사와 physics-aware rollback을 통해 실현 가능성을 강화하여 최종 토큰이 물리 법칙과 조립 제약 조건을 준수하는지 확인하였다.
Dataset: StableText2Lego
LEGO 표현
LEGO 베이스플레이트 위에 만들어진 LEGO 구조물을 고려한다. StableText2Lego의 각 LEGO 구조물은 $B = [b_1, \ldots, b_N]$으로 표현되며, $N$개의 브릭을 포함하고, 각 $b_i$는 브릭의 상태를 $b_i = [h_i, w_i, x_i, y_i, z_i]$로 나타낸다. $h_i$와 $w_i$는 $X$ 방향과 $Y$ 방향의 브릭 길이이다. $x_i$, $y_i$, $z_i$는 원점에 가장 가까운 스터드의 위치를 나타낸다. 위치는 $x_i, y_i, z_i \in [0, \ldots, 19]$이다.
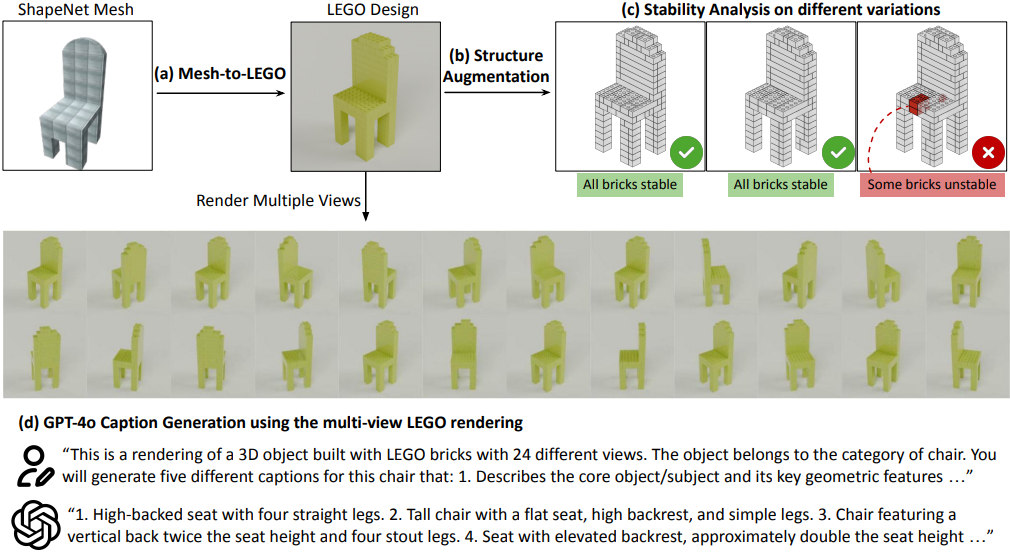
Mesh-to-LEGO
저자들은 ShapeNetCore의 3D shape을 LEGO 구조로 변환하여 데이터셋을 구성하였다. 3D 메쉬가 주어지면 voxelize하고 20$\times$20$\times$20 그리드로 다운샘플링하여 일관된 크기를 보장한다. LEGO 블록 레이아웃은 split-and-remerge legolization으로 생성된다. 데이터 품질과 다양성을 개선하기 위해 legolization에 랜덤성을 도입하고, 동일한 3D 물체에 대해 여러 개의 다른 LEGO 구조를 생성한다. 이렇게 하면 안정적인 LEGO 구조와 더 다양한 LEGO 블록 레이아웃을 얻을 가능성이 높아진다. 일반적으로 사용 가능한 8가지 표준 블록 (1$\times$1, 1$\times$2, 1$\times$4, 1$\times$6, 1$\times$8, 2$\times$2, 2$\times$4, 2$\times$6)을 사용한다.
안정성 점수
각 구조물의 물리적 안정성을 StableLego의 분석 방법을 사용하여 평가한다. 안정성 점수 $S \in \mathbb{R}^N$은 각 브릭 $b_i$에 연결부의 내부 응력을 정량화하는 값 $s_i \in [0,1]$를 할당한다. $s_i$가 높을수록 안정성이 높고, $s_i = 0$이면 구조적 파괴를 일으키는 불안정한 브릭을 나타낸다. 안정성 점수를 계산하려면 구조적 붕괴를 방지하는 정적 평형을 달성하기 위해 각 브릭에 작용하는 힘을 결정하는 비선형 프로그램을 풀어야 한다. 일반적인 크기의 구조물(200개 미만의 브릭)의 경우 평균 약 0.35초가 소요되며, 모든 브릭의 안정성 점수가 0보다 큰 안정적인 구조물만 데이터셋에 포함하였다.
캡션 생성
각 도형에 대한 캡션을 얻기 위해 24개의 서로 다른 시점에서 LEGO를 렌더링하고 이를 하나의 멀티뷰 이미지로 결합한다. 그런 다음 GPT-4o가 이러한 렌더링에 대해 다양한 수준의 디테일을 포함하는 다섯 가지 설명을 생성하도록 한다.저자들은 GPT-4o가 색상 정보를 생략하고 형상 구조에만 집중하도록 하였다. 각 카테고리 내의 풍부하고 포괄적인 텍스트-LEGO 쌍을 통해 대규모 생성 모델을 학습시킬 수 있다.

Method
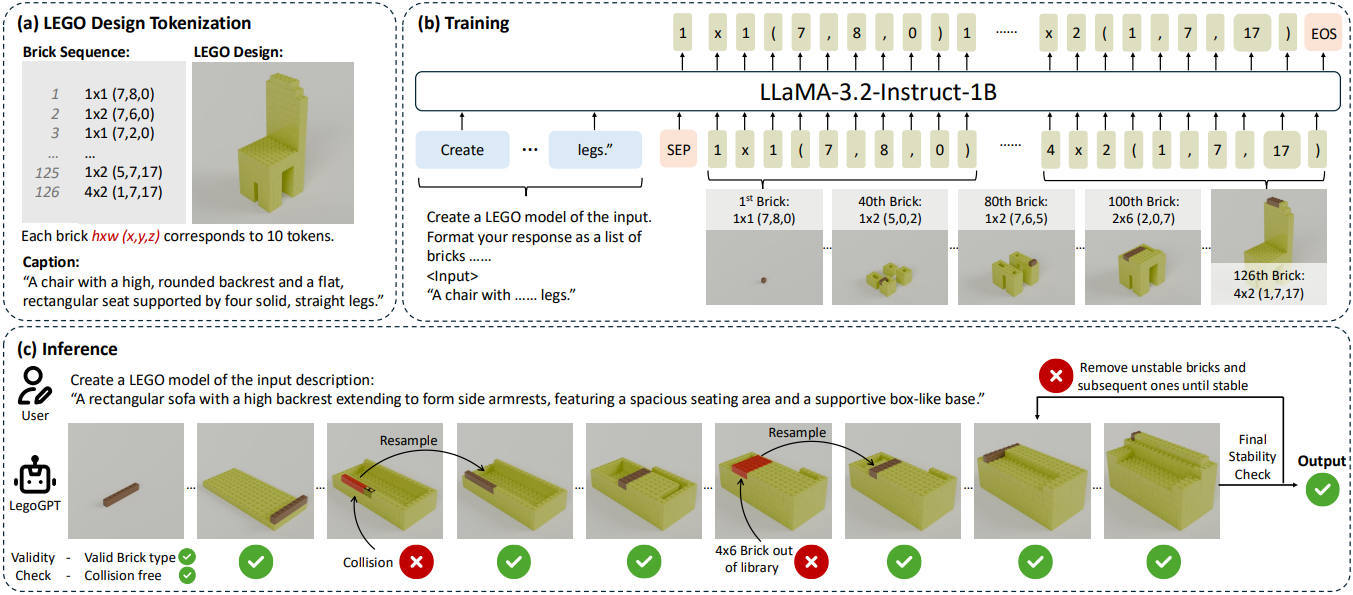
1. Model Fine-tuning
사전 학습된 LLM은 시퀀스 모델링과 자연어 이해에 탁월하여 본 논문의 목표에 적합하다. StableText2Lego의 텍스트 프롬프트와 해당 LEGO 구조가 포함된 커스텀 instruction 데이터셋을 기반으로 사전 학습된 LLM을 fine-tuning한다.
Base model 사전 학습
LLaMA-3.2-1B-Instruct를 base model로 사용한다. 이 모델은 instruction 프롬프트에 대한 일관된 답변을 제공하도록 fine-tuning되어 텍스트 기반 LEGO 디자인 생성에 적합하다. Base model은 in-context learning을 통해 LEGO와 유사한 디자인을 생성할 수 있다. 그러나 생성된 디자인은 특정 부분이 누락되거나 교차하거나 분리된 블록을 포함하는 경우가 많아 물리적으로 불안정하고 조립이 불가능하다. 이러한 문제를 해결하기 위해 데이터셋을 사용하여 사전 학습된 모델을 더욱 fine-tuning한다.
Instruction fine-tuning 데이터셋
저자들은 각각의 안정적인 디자인과 그에 해당하는 캡션에 대해 다음과 같은 형식으로 instruction을 구성하였다.
“(user) Create a LEGO model of {caption}. (assistant) {lego-design}.”
학습을 단순화하고 LLaMA의 tokenizer를 재사용하기 위해, LEGO 디자인을 일반 텍스트로 표현한다. 표준 LEGO 디자인 형식인 LDraw에는 두 가지 주요 단점이 있다.
- 구조를 평가하고 브릭 배치를 검증하는 데 중요한 브릭 치수를 직접 포함하지 않는다.
- 브릭 방향과 스케일과 같은 불필요한 정보를 포함한다. 축에 정렬된 각 브릭은 두 가지 유효한 방향만 가지므로 이러한 정보는 불필요하다.
저자들은 LDraw를 사용하는 대신, LEGO 블록 하나를 “\(\{h\}\times\{w\} (\{x\},\{y\},\{z\})\)“로 나타낸다. 모든 블록은 높이가 1인 직육면체이며, 축에 정렬되어 있으며, $h$와 $w$의 순서는 수직축을 기준으로 블록의 방향을 나타낸다. 이 형식은 디자인을 표현하는 데 필요한 토큰 수를 크게 줄이는 동시에 3D 추론에 필수적인 블록 치수 정보를 포함한다. 블록은 raster-scan 방식으로 아래에서 위로 정렬된다.
Fine-tuning된 모델 LegoGPT $\theta$를 사용하여 브릭 $b_1, \ldots, b_N$을 autoregressive한 방식으로 예측한다.
\[\begin{equation} p(b_1, b_2, \ldots, b_N \vert \theta) = \prod_{i=1}^N p (b_i \vert b_1, \ldots, b_{i-1}, \theta) \end{equation}\]2. Integrating Physical Stability
물리적으로 안정적인 데이터를 기반으로 학습되었지만, 본 모델은 때때로 물리적 제약이나 조립 제약을 위반하는 디자인을 생성한다. 저자들은 이 문제를 해결하기 위해, autoregressive한 inference에 물리적 안정성 검증을 추가로 통합했다.
LEGO 구조물은 베이스플레이트 위에 건축할 때 붕괴되지 않으면 물리적으로 안정적이고 건축 가능한 것으로 간주된다. 이를 위해, StableLego의 안정성 분석 방법을 사용하여 물리적 구조 안정성을 평가한다.
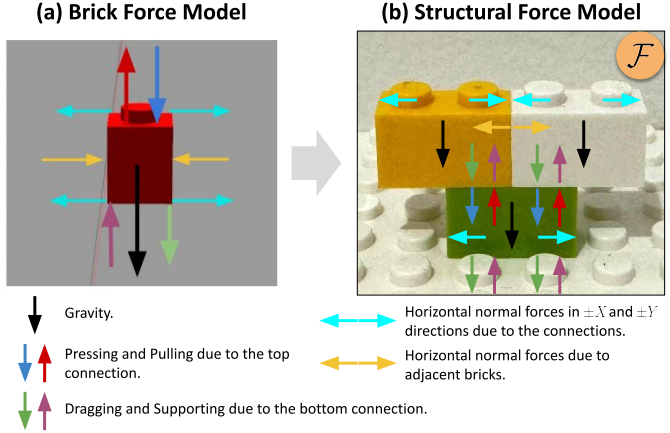
위 그림은 브릭에 가해질 수 있는 모든 힘을 보여준다. 일련의 힘 후보들로 구성된 구조력(structural force) 모델 $\mathcal{F}$를 도출한다. 각 브릭 $b_i$는 $M_i$개의 힘 후보 \(F_i^j \in \mathcal{F}_i, j \in [1, M_i]\)를 가진다. 모든 브릭이 정적 평형에 도달할 수 있는 경우를 구조가 안정적이라고 한다.
($L_i^j$는 $F_i^j$에 대응하는 해당하는 작용점 길이)
안정성 해석은 다음과 같이 비선형 프로그램으로 공식화된다.
\[\begin{equation} \underset{\mathcal{F}}{\arg \min} \sum_i^N \left\{ \vert \sum_j^{M_i} F_i^j \vert + \vert \sum_j^{M_i} \tau_i^j \vert + \alpha \mathcal{D}_i^\textrm{max} + \beta \sum \mathcal{D}_i \right\} \end{equation}\](\(\mathcal{D}_i \subset \mathcal{F}_i\)는 dragging force 후보들)
세 가지 제약 조건이 적용된다.
- $\mathcal{F}$의 모든 힘 후보는 음이 아닌 값을 가져야 한다.
- 같은 브릭에 작용하는 특정 힘은 공존할 수 없다. (ex. 빨간색/파란색 화살표, 녹색/보라색 화살표)
- 뉴턴의 제 3법칙에 따라, 위쪽 브릭에 작용하는 지지력은 아래쪽 브릭에 작용하는 누르는 힘과 같아야 한다.
위의 비선형 프로그램을 Gurobi를 사용하여 풀면 최소 내부 응력으로 정적 평형 상태로 유도하고, 전체 마찰력 \(\sum \mathcal{D}_i\)을 억제하며, 극한값 \(\mathcal{D}_i^\textrm{max}\)를 방지하는 힘 분포 $\mathcal{F}$를 구할 수 있다. 힘 분포 $\mathcal{F}$로부터 브릭별 안정성 점수는 다음과 같다.
\[\begin{equation} s_i = \begin{cases} 0 & \sum_j^{M_i} F_i^j \ne 0 \, \vee \, \sum_j^{M_i} \tau_i^j \ne 0 \, \vee \, \mathcal{D}_i^\textrm{max} > F_T \\ \frac{F_T - \mathcal{D}_i^\textrm{max}}{F_T} & \textrm{otherwise} \end{cases} \end{equation}\]($F_T$는 브릭 접합부 사이의 측정된 friction capacity)
안정성 점수 $s_i$가 높을수록 안정성이 높고, $s_i = 0$은 구조적 파괴를 유발하는 불안정한 브릭을 나타낸다. 즉, $\mathcal{F}$가 정적 평형에 도달할 수 없거나 필요한 마찰력이 재료의 friction capacity을 초과한다. 물리적으로 안정적인 구조의 경우, 모든 브릭에 대해 $s_i > 0$이어야 한다.
안정성 분석을 언제 적용해야 할까?
모델은 한 번에 LEGO 블록 하나씩 순차적으로 LEGO 디자인을 생성한다. 물리적 안정성을 보장하는 간단한 방법은 각 단계에 안정성 분석을 적용하고 붕괴를 유발할 수 있는 블록을 다시 샘플링하는 것이다. 이러한 단계별 검증은 각 단계가 효율적이지만, 필요한 검사 횟수가 많기 때문에 시간이 많이 소요될 수 있다. 더 중요한 것은, 많은 LEGO 디자인이 부분적으로 제작되었을 때는 불안정하지만 완전히 조립되면 안정된다는 것이다. 각 블록 생성 후 안정성 검사를 추가하면 모델 탐색 공간이 지나치게 제한될 수 있다. 따라서 저자들은 안정성과 다양성의 균형을 맞추기 위해 physics-aware rollback과 결합된 brick-by-brick rejection sampling을 제안하였다.
Brick-by-Brick Rejection Sampling
Inference 속도를 개선하고 모델 생성을 지나치게 제한하지 않기 위해 inference 중에 제약 조건을 완화한다.
- 모델이 LEGO 블록과 그 위치를 생성할 때 블록은 형식을 잘 따라야 하며 작업 공간 밖에 있어서는 안 된다.
- 새로 추가된 블록이 기존 구조와 충돌하지 않아야 한다.
이러한 휴리스틱을 사용하면 복잡한 물리적 안정성을 명시적으로 고려하지 않고도 잘 포맷된 LEGO 구조를 효율적으로 생성할 수 있다. 이러한 휴리스틱을 통합하기 위해 rejection sampling을 사용한다. 블록이 휴리스틱을 위반하면 모델에서 새 블록을 다시 샘플링한다. 완화된 제약 조건으로 인해 대부분의 블록이 유효하고 rejection sampling이 inference 시간에 큰 영향을 미치지 않는다.
Physics-Aware Rollback
최종 디자인 $B$가 물리적으로 안정되도록 안정성 점수 $S$를 계산한다. 결과 설계가 불안정하면, 즉 $s_i = 0$인 브릭이 있다면 불안정 브릭이 생성되기 전 상태인 $B^\prime$으로 디자인을 롤백한다. 안정적인 구조 $B^\prime$에 도달할 때까지 이 프로세스를 반복적으로 반복하고 부분 구조 $B^\prime$에서 생성을 계속한다. 브릭별 안정성 점수를 사용하기 때문에 붕괴되는 브릭과 해당 인덱스를 효율적으로 찾을 수 있다.

3. LEGO Texturing and Coloring
주된 목표는 LEGO 형태를 만드는 것이지만, 색상과 텍스처 또한 창의적인 LEGO 디자인에서 중요한 역할을 한다. 따라서 저자들은 개별 브릭에 섬세한 UV 텍스처를 적용하거나 균일한 색상을 부여하는 방법을 제안하였다.
UV 텍스처 생성
구조 $B$와 그에 대응하는 메쉬 $\mathcal{M}$이 주어졌을 때, 먼저 인접한 브릭으로 여섯 면이 모두 가려진 브릭들을 찾아 제거한다. 남은 브릭은 ImportLDraw를 사용하여 하나의 메쉬 $\mathcal{M}$으로 병합한다. Cube projection을 통해 UV map \(\textrm{UV}_\mathcal{M}\)을 생성한다. 그런 다음, 빠른 텍스트 기반 메쉬 텍스처링 방식인 FlashTex를 사용하여 텍스처 맵 \(I_\textrm{texture}\)를 생성한다.
\[\begin{equation} I_\textrm{texture} = \textrm{FlashTex} (\mathcal{M}, \textrm{UV}_\mathcal{M}, c) \end{equation}\]균일한 브릭 색상 지정
각 브릭에 균일한 색상을 할당할 수도 있다. 구조 $B$가 주어지면, 이를 복셀 그리드 $\mathcal{V}$로 변환한 후 UV-unwrapped mesh \(\mathcal{M}_\mathcal{V}\)로 변환한다. 모든 복셀 \(v \in \mathcal{V}\)에 대해, $f_i^v$를 보이는 면이라 하면 ($i = 1, \ldots, N_v$), 각 $f_i^v$는 두 개의 삼각형으로 분할되어 UV 영역 \(\mathcal{S}_i^v\)에 매핑되어 UV map \(\textrm{UV}_\mathcal{V}\)를 갖는 메쉬 \(\mathcal{M}_\mathcal{V}\)를 생성한다. FlashTex를 적용하여 텍스처 \(I_\textrm{texture}\)를 생성한다.
\[\begin{equation} I_\textrm{texture} = \textrm{FlashTex} (\mathcal{M}_\mathcal{V}, \textrm{UV}_\mathcal{V}, c) \end{equation}\]각 복셀의 색상 $\mathcal{C}(v) \in \mathbb{R}^3$은 다음과 같이 계산된다.
\[\begin{equation} \mathcal{C} (v) = \frac{1}{N_v} \sum_{i=1}^{N_v} \mathcal{C}(f_i^v), \quad \forall v \in \mathcal{V} \\ \textrm{where} \quad \mathcal{C}(f_i^v) \frac{1}{\vert \mathcal{S}_i^v \vert} \sum_{(x,y) \in \mathcal{S}_i^v} I_\textrm{texture} (x, y) \end{equation}\]($\mathcal{C}(f_i^v)$는 $f_i^v$의 색상, \(\vert \mathcal{S}_i^v \vert\)는 UV map에서 영역 \(\mathcal{S}_i^v\)의 픽셀 수)
각 브릭 $b_t$와 그 구성 복셀 \(\mathcal{V}_t\)에 대해, 브릭 색상을 계산한다.
\[\begin{equation} \mathcal{C}(b_t) = \frac{1}{\vert \mathcal{V}_t \vert} \mathcal{C} (v) \end{equation}\]마지막으로 색상 세트에서 가장 가까운 색상을 찾는다. UV 텍스처링은 더욱 정확한 디테일을 제공하지만, 균일한 색상은 표준 LEGO 브릭을 사용할 수 있게 해준다.
Experiments
- 구현 디테일
- 최대 토큰 수: 4,096
- $F_T$ = 0.98N, $\alpha = 10^{-3}$, $\beta = 10^{-6}$
- 최대 100번의 physics-aware rollback
1. LEGO Generation Results
다음은 다른 방법들과 비교한 결과이다.
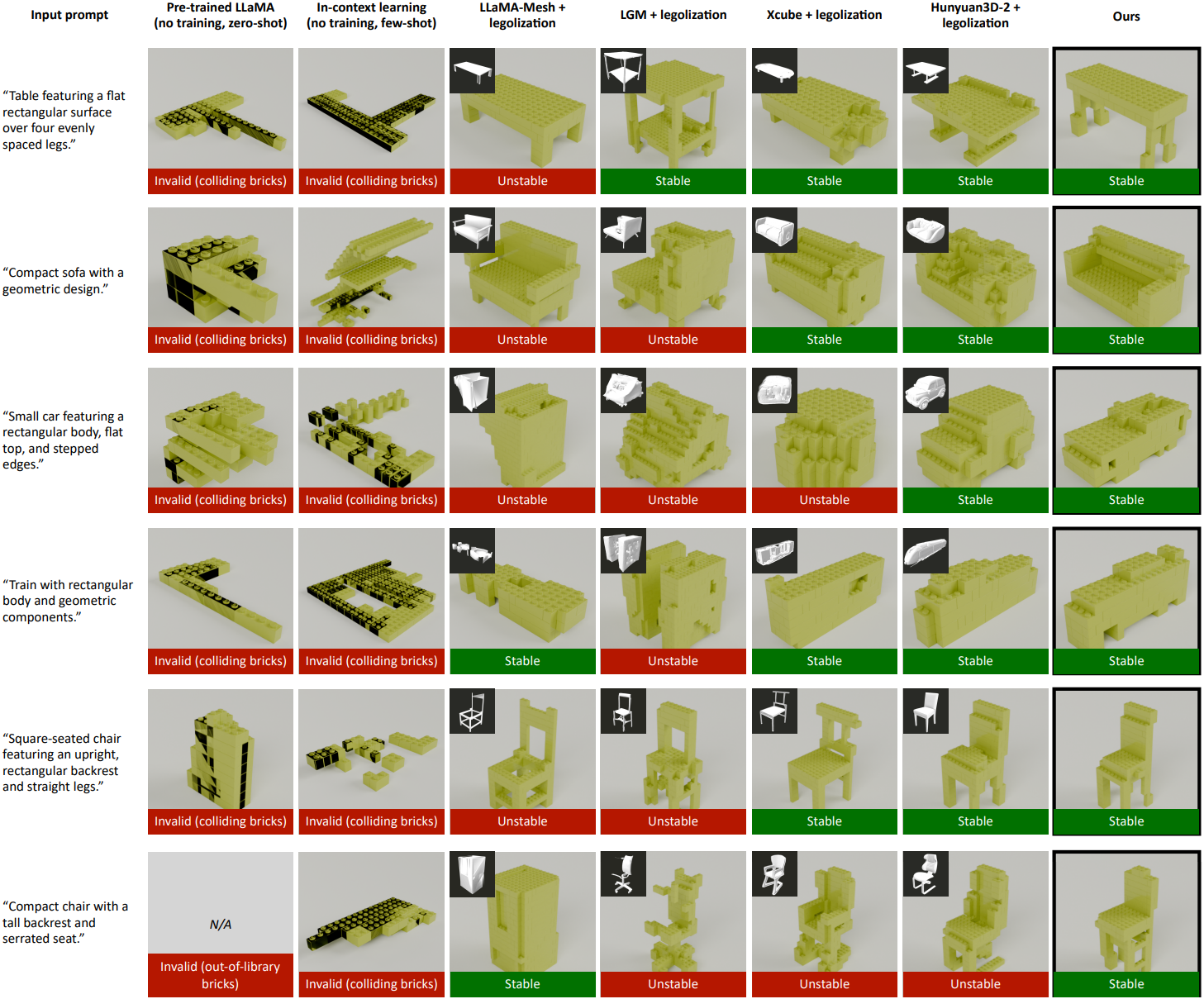
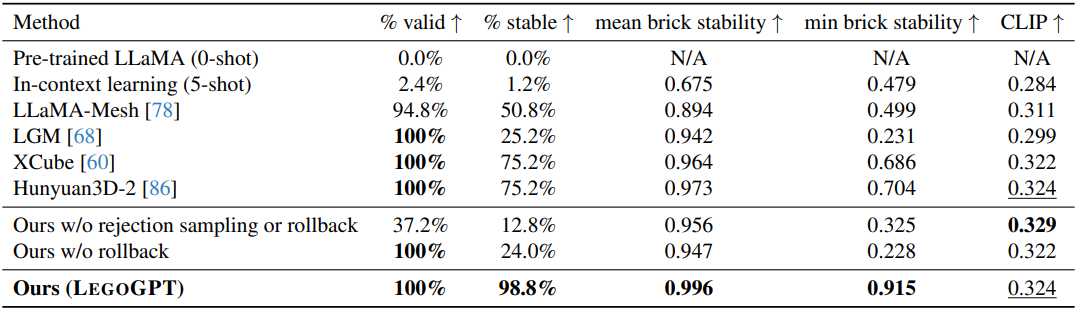
다음은 ablation study 결과이다.

2. Extensions and Applications
다음은 로봇을 활용한 자동 조립의 예시들이다.

다음은 텍스처 또는 색상이 있는 생성 결과이다.

Limitations
- 21개 카테고리에 걸쳐 20$\times$20$\times$20 그리드 내에서 디자인을 생성하는 데 국한된다.
- 고정된 레고 블록 세트만을 지원한다.