[논문리뷰] LEDITS++: Limitless Image Editing using Text-to-Image Models

CVPR 2024. [Paper] [Page] [Code]
Manuel Brack, Felix Friedrich, Katharina Kornmeier, Linoy Tsaban, Patrick Schramowski, Kristian Kersting, Apolinário Passos
DFKI | TU Darmstadt | Hessian.AI | Hugging Face | LAION
28 Nov 2023

Introduction

Diffusion model은 텍스트 설명에서 고품질 이미지를 생성하는 능력으로 인정을 받았다. 최근 실제 이미지를 조작하기 위해 이러한 모델을 활용하는 연구가 점점 늘어나고 있다. 그러나 여러 가지 장벽으로 인해 diffusion 기반 이미지 편집을 실제로 적용할 수 없다. 현재 방법은 계산 비용이 많이 드는 모델 튜닝이나 기타 최적화를 수반하여 실질적인 문제를 가지고 있다. 또한 기존 기술은 원본 이미지에 큰 변화를 가져오는 경향이 있어 종종 완전히 다른 이미지를 생성한다. 마지막으로, 이러한 모든 접근 방식은 임의의 여러 개념을 동시에 편집할 때 본질적으로 제한된다. 본 논문은 이러한 한계를 해결하는 diffusion 기반 이미지 편집 기술인 LEDITS++를 도입하여 이러한 문제를 해결하였다.

LEDITS++는 텍스트 이미지 편집을 위한 간소화된 접근 방식을 제공하므로 광범위한 파라미터 튜닝이 필요하지 않다. 이를 위해 저자들은 계산 자원을 대폭 줄이고 완벽한 이미지 재구성을 보장하기 위해 보다 효율적인 diffusion 샘플링 알고리즘을 위한 이미지 inversion을 유도하였다. 따라서 계산상의 장애물을 극복하고 편집된 이미지의 변경을 우선적으로 방지한다. 또한, 새로운 implicit한 마스킹 접근 방식을 사용하여 각 편집 명령을 관련된 이미지 영역에 할당한다 (Semantic Grounding). 이는 전체 이미지 구성과 물체의 identity를 유지하여 이미지 변경을 더욱 최적화한다. 또한 LEDITS++는 과도한 간섭을 일으키지 않고 여러 동시 명령을 지원하여 쉽고 다양한 이미지 편집을 용이하게 하는 유일한 방법이다. 마지막으로 가볍고 아키텍처에 구애받지 않는 특성으로 인해 latent 및 픽셀 기반 diffusion model과의 호환성이 보장되어 다양한 애플리케이션에 대한 높은 접근성을 제공한다.

본 논문은 LEDITS++의 체계적인 이점을 확립하고 이 직관적이고 가벼운 접근 방식이 이미지 편집을 위한 정교한 semantic 제어를 제공한다는 것을 보여준다. 특히, LEDITS++의 정의를 고안하고 보다 효율적인 diffusion 샘플링 방법을 위한 완벽한 inversion을 도출하였으며 LEDITS++의 효율성, 다양성, 정밀도를 입증하였다. 또한 텍스트 이미지 조작을 평가하기 위한 보다 전체적이고 일관된 테스트베드인 Textual Editing Benchmark++ (TEdBench++)를 도입하였다.

Image Editing with Text-to-Image Models

1. Guided Diffusion Models

Diffusion model은 반복적으로 Gaussian noise를 제거하여 학습된 데이터 분포의 샘플을 생성한다. 이미지 $x_0$를 점진적으로 Gaussian noise로 바꾸는 diffusion process를 고려해 보자.

\[\begin{equation} x_t = \sqrt{1 - \beta_t} x_{t-1} + \sqrt{\beta_t} n_t, \quad t = 1, \ldots, T \end{equation}\]

여기서 $n_t$는 정규 분포 벡터이고 $\beta_t$는 variance schedule이다. 일반적으로 diffusion process는 다음과 같이 등가적으로 표현된다.

\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon_t \\ \quad \alpha_t = 1 - \beta_t, \; \bar{\alpha}_t = \prod_{s=1}^t \alpha_s, \; \epsilon_t \sim \mathcal{N} (0, \mathbf{I}) \end{equation}\]

중요한 것은 모든 $\epsilon_t$가 통계적으로 독립적이지 않다는 것이다. 대신, 연속적인 쌍 $\epsilon_t$, \(\epsilon_{t-1}\)은 강하게 종속적이며 이는 나중에 관련된다. 새로운 이미지 \(\hat{x}_0\)를 생성하기 위해 reverse process는 랜덤 노이즈 $x_T \sim \mathcal{N} (0, \mathbf{I})$에서 시작하며, 다음과 같이 반복적으로 denoise할 수 있다.

\[\begin{equation} x_{t-1} = \hat{\mu}_t (x_t) + \sigma_t z_t, \quad t = T, \ldots, 1 \end{equation}\]

여기서 $z_t$는 정규 분포 벡터이고 공통 variance schedule $\sigma_t$는 다음과 같은 표현될 수 있다.

\[\begin{equation} \sigma_t = \eta \beta_t \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t}, \quad \eta \in [0, 1] \end{equation}\]

이 공식에서 $\eta = 0$은 deterministic한 DDIM에 해당하고 $\eta = 1$은 DDPM에 해당한다. $\mu_t (x_t)$는 다음과 같다.

\[\begin{equation} \mu_t (x_t) = \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \frac{x_t - \sqrt{1 - \bar{\alpha}_t} \hat{\epsilon}_\theta (x_t)}{\sqrt{\vphantom{1} \bar{\alpha}_t}} + \sqrt{1 - \bar{\alpha}_{t-1} - \sigma_t^2} \hat{\epsilon}_\theta (x_t) \end{equation}\]

여기서 \(\hat{\epsilon}_\theta (x_t)\)는 일반적으로 U-Net으로 구현되는 학습된 파라미터 $\theta$를 사용하여 diffusion model에서 생성된 $\epsilon_t$의 추정치이다. Text-to-image 생성의 경우 모델은 해당 프롬프트에 충실한 이미지를 생성하기 위해 텍스트 프롬프트 $p$로 컨디셔닝된다. Diffusion model은 반복적으로 \(\hat{x}_0\)을 샘플링하는 데 필요한 noise 추정치 \(\hat{\epsilon}_\theta (x_t)\)를 생성하도록 학습되었다. 텍스트로 컨디셔닝된 diffusion model의 경우 \(\hat{\epsilon}_\theta\)는 특정 guidance 기술을 사용하여 계산된다.

대부분의 diffusion model은 순수한 diffusion model을 사용하는 컨디셔닝 방법인 classifier-free guidance에 의존하므로 추가 classifier가 필요하지 않다. 학습 중에 텍스트 컨디셔닝 $c_p$는 고정된 확률로 무작위로 제거되어 unconditional한 목적 함수와 conditional한 목적 함수에 대한 결합 모델이 생성된다. Inference 중에 $\epsilon$-예측에 대한 score 추정치는 다음과 같이 조정된다.

\[\begin{equation} \hat{\epsilon}_\theta (x_t, c_p) := \hat{\epsilon}_\theta (x_t) + s_g (\hat{\epsilon}_\theta (x_t, c_p) - \hat{\epsilon}_\theta (x_t)) \end{equation}\]

Guidance scale $s_g$와 \(\hat{\epsilon}_\theta\)를 사용하여 파라미터 $\theta$로 noise 추정치를 정의한다. 직관적으로, unconditional한 $\epsilon$-예측은 conditional한 $\epsilon$-예측의 방향으로 밀리고 $s_g$는 조정 범위를 결정한다.

2. LEDITS++

LEDITS++의 방법론은 (1) 효율적인 이미지 inversion, (2) 다양한 텍스트 편집, (3) 이미지 변경의 semantic grounding이라는 세 가지 구성 요소로 나눌 수 있다.

구성 요소 1: 완벽한 Inversion

실제 이미지를 편집하기 위해 text-to-image 모델을 활용하려면 입력 이미지 생성을 컨디셔닝해야 한다. 최근 연구에서는 입력 이미지 $x_0$로 denoise될 $x_T$를 식별하기 위해 샘플링 프로세스를 반전시키는 데 크게 의존해 왔다. DDPM scheduler를 반전시키는 것이 일반적으로 DDIM inversion보다 선호되며, 이는 더 적은 timestep으로 재구성 오차 없이 달성할 수 있기 때문이다.

그러나 필요한 step 수와 결과적으로 diffusion model 평가 횟수를 크게 줄이는 diffusion model 샘플링을 위해 DDPM보다 더 효율적인 체계가 있다. 저자들은 그러한 체계에 대해 원하는 inversion 속성을 도출하여 보다 효율적인 inversion 방법을 제안하였다. DDPM은 reverse process를 SDE로 공식화할 때 1차 SDE solver로 볼 수 있다. 이 SDE는 고차 미분 방정식 솔버(dpm-solver++)를 사용하여 더 적은 단계로 더 효율적으로 풀 수 있다. 2차 sde-dpm-solver++에 대한 reverse process는 다음과 같이 쓸 수 있다.

\[\begin{equation} x_{t-1} = \hat{\mu}_t (x_t, x_{t+1}) + \sigma_t z_t, \quad t = T, \ldots, 1 \\ \textrm{where} \quad \sigma_t = \sqrt{1 - \bar{\alpha}_{t-1}} \sqrt{1 - e^{-2h_{t-1}}} \end{equation}\]

여기서 $h_t$는 다음과 같다.

\[\begin{equation} h_t = \frac{\textrm{ln} (\sqrt{\vphantom{1} \bar{\alpha}_t})}{\textrm{ln} (\sqrt{1 - \bar{\alpha}_t})} - \frac{\textrm{ln} (\sqrt{\vphantom{1} \bar{\alpha}_{t+1}})}{\textrm{ln} (\sqrt{1 - \bar{\alpha}_{t+1}})} \end{equation}\]

이제 \(\hat{\mu}_t\)는 2개의 timestep에 대한 $x$, 즉 $x_t$와 $x_{t+1}$에 의존한다.

\[\begin{aligned} \hat{\mu}_t (x_t, x_{t+1}) &= \frac{\sqrt{1 - \bar{\alpha}_{t-1}}}{\sqrt{1 - \bar{\alpha}_t}} e^{-h_{t-1}} x_t + \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} (1 - e^{-2h_{t-1}}) \hat{\epsilon}_\theta (x_t) \\ &+ 0.5 \sqrt{\vphantom{1} \bar{\alpha}_{t-1}} (1 - e^{-2h_{t-1}}) \frac{- h_t}{h_{t-1}} (\hat{\epsilon}_\theta (x_{t+1}) - \hat{\epsilon}_\theta (x_t)) \end{aligned}\]

위의 내용을 바탕으로 inversion 프로세스를 고안할 수 있다. 입력 이미지 $x_0$가 주어지면 noise 이미지 $x_1, \ldots x_T$의 보조 재구성 시퀀스를 다음과 같이 구성한다.

\[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \tilde{\epsilon}_t, \quad \tilde{\epsilon}_t \sim \mathcal{N}(0,\mathbf{I}) \end{equation}\]

\(\tilde{\epsilon}_t\)는 이제 통계적으로 독립적이며 이는 이미지 편집에 바람직한 속성이다. 마지막으로, inversion에 대한 각각의 $z_t$는 다음과 같이 도출될 수 있다.

\[\begin{equation} z_t = \frac{x_{t-1} - \hat{\mu}_t (x_t, x_{t+1})}{\sigma_t}, \quad t = T, \ldots, 1 \end{equation}\]

저자들은 이전 step의 추정치를 재사용하여 각 timestep에서 diffusion model을 한 번만 평가하면 되는 sde-dpm-solver++의 변형을 기반으로 구현했다. 중간 step $t < T$에서 inversion을 중지하고 해당 step에서 생성을 시작하면 timestep을 더 줄일 수 있다. 경험적으로, $t \in [0.9T, 0.8T]$가 일반적으로 $t = T$와 동일한 충실도의 편집을 생성했으며, 이는 이전 timestep가 편집과 덜 관련된다는 관찰을 뒷받침한다.

구성 요소 2: 텍스트 편집

재구성 시퀀스 $x_1, \ldots, x_T$를 생성하고 각각의 $z_t$를 계산한 후 편집 명령 집합 \(\{e_i\}_{i \in I}\)를 기반으로 noise 추정값 \(\hat{\epsilon}_\theta\)를 조작하여 이미지를 편집한다. 저자들은 conditional한 추정치와 unconditional한 추정치를 기반으로 각 개념 $e_i$에 대한 전용 guidance 항을 고안하였다. 단일 편집 프롬프트 $e$에서 시작하여 LEDITS++의 guidance를 정의한다.

\[\begin{equation} \hat{\epsilon}_\theta (x_t, c_e) := \hat{\epsilon}_\theta (x_t) + \gamma (x_t, c_e) \end{equation}\]

여기서 $\gamma$는 guidance 항이다. 결과적으로 $\gamma = 0$으로 설정하면 입력 이미지 $x_0$가 재구성된다. Unconditional score 추정치 \(\hat{\epsilon}_\theta (x_t)\)를 guidance 방향에 따라 편집 개념 추정치 \(\hat{\epsilon}_\theta (x_t, c_e)\)에서 멀어지거나 가까워지도록 푸시하기 위해 $\gamma$를 다음과 같이 구성한다.

\[\begin{equation} \gamma (x_t, c_e) = \phi (\psi; s_e, \lambda) \psi(x_t, c_e) \end{equation}\]

여기서 $\psi$는 편집 guidance scale $s_e$를 요소별로 적용하고 $\psi$는 편집 방향에 따라 달라진다.

\[\begin{equation} \psi (x_t, c_e) = \begin{cases} \hat{\epsilon}_\theta (x_t, c_e) - \hat{\epsilon}_\theta (x_t) & \quad \textrm{if pos. guidance} \\ -(\hat{\epsilon}_\theta (x_t, c_e) - \hat{\epsilon}_\theta (x_t)) & \quad \textrm{if neg. guidance} \\ \end{cases} \end{equation}\]

따라서 guidance 방향 변경은 \(\hat{\epsilon}_\theta (x_t, c_e)\)와 \(\hat{\epsilon}_\theta (x_t)\) 사이의 방향에 반영된다. $\phi$ 항은 프롬프트 $e$와 관련된 이미지의 크기와 각각의 \(\hat{\epsilon}_\theta (x_t, c_e)\)를 식별한다. 결과적으로, $\phi$는 관련 없는 모든 차원에 대해 0을 리턴하고 다른 차원에 대해서는 scaling factor $s_e$를 리턴한다. $s_e$가 클수록 편집 효과가 증가하며 $\lambda \in (0, 1)$은 $\phi$에 의해 관련성 있는 것으로 선택된 픽셀의 백분율을 반영한다. 특히, 하나의 개념 $e$와 균일한 $\phi = s_e$의 경우 \(\hat{\epsilon}_\theta (x_t, c_e)\)는 classifier-free guidance 항으로 일반화된다.

여러 개념들 $e_i$에 대해서는 위에서 설명한 대로 $\gamma_t^i$를 계산하며, 각 개념들은 각각의 hyperparameter 값 $\lambda^i$, $s_e^i$를 정의한다. 모든 $\gamma_t^i$의 합은 다음과 같다.

\[\begin{equation} \hat{\gamma}_t (x_t, c_{e_i}) = \sum_{i \in I} \gamma_t^i (x_t, c_{e_i}) \end{equation}\]

구성 요소 3: Semantic Grounding

마스킹 항 $\phi$는 scaling factor $s_e$와 결합된 바이너리 마스크 $M^1$과 $M^2$의 교집합(pointwise product)이다.

\[\begin{equation} \phi (\psi; s_{e_i}, \lambda) = s_{e_i} M_i^1 M_i^2 \end{equation}\]

여기서 $M_i^1$는 U-Net의 cross-attention layer에서 생성된 바이너리 마스크이고 $M_i^2$는 noise 추정치에서 파생된 바이너리 마스크이다. 직관적으로 각 마스크는 중요도 맵이며, $M_i^1$는 $M_i^2$보다 더 강력하지만 훨씬 더 대략적이다. 따라서 이 둘의 교집합은 관련 이미지 영역에 초점을 맞추고 세밀한 마스크를 생성한다. 이러한 맵들은 아직 존재하지 않는 편집 개념과 관련된 이미지 영역을 캡처할 수도 있다. 특히 여러 편집의 경우 각 편집 프롬프트에 대한 전용 마스크를 계산하면 해당 guidance 항이 크게 격리되어 상호 간섭이 제한된다.

각 timestep $t$에서 편집 프롬프트 $e_i$와 함께 U-Net forward pass가 수행되어 편집 프롬프트의 각 토큰에 대한 cross-attention map을 생성한다. 가장 작은 해상도(ex. SD의 경우 16$\times$16)의 모든 cross-attention map은 모든 head와 레이어에 대해 평균화되고 결과 맵은 모든 편집 토큰에 대해 합산되어 하나의 맵 \(A_t^{e_i} \in \mathbb{R}^{16 \times 16}\)이 된다. 중요한 것은 최소한의 오버헤드로 $M^1$을 생성하기 위해 앞서 이미 수행된 U-Net 평가 \(\hat{\epsilon}_\theta (x_t, c_e)\)를 활용한다는 것이다. 각 맵 \(A_t^{e_i}\)는 $x_t$의 크기와 일치하도록 업샘플링된다. Cross-attention mask $M^1$은 업샘플링된 \(A_t^{e_i}\)의 $\lambda$번째 백분위수를 계산하여 도출된다.

\[\begin{equation} M_i^1 = \begin{cases} 1 & \quad \textrm{if} \; \vert A_t^{e_i} \vert \ge \eta_\lambda (\vert A_t^{e_i} \vert) \\ 0 & \quad \textrm{else} \end{cases} \end{equation}\]

여기서 $\eta_\lambda (\vert \cdot \vert)$는 $\lambda$번째 백분위수이다. 정의에 따라 $M^1$은 편집 프롬프트와 밀접하게 연관되는 이미지 영역만 선택하고 $\lambda$는 이 선택된 영역의 크기를 결정한다.

세밀한 마스크 $M^2$는 noise 추정치의 guidance 벡터 $\psi$를 기반으로 계산된다. Unconditional한 \(\hat{\epsilon}_\theta\)와 conditional한 \(\hat{\epsilon}_\theta\)의 차이는 일반적으로 $x_t$의 윤곽선과 물체 가장자리를 캡처한다. 결과적으로, $\psi$의 가장 큰 절대값은 $M^2$를 위한 세밀하고 의미 있는 분할 정보를 제공한다.

\[\begin{equation} M^2 = \begin{cases} 1 & \quad \textrm{if} \; \vert \psi \vert \ge \eta_\lambda (\vert \psi \vert) \\ 0 & \quad \textrm{else} \end{cases} \end{equation}\]

일반적으로 threshold $\lambda$는 수행된 편집과 일치해야 한다. Style transfer와 같이 전체 이미지에 영향을 미치는 변경 사항은 더 작은 $\lambda(\rightarrow 0)$를 선택해야 하는 반면, 특정 물체나 영역을 대상으로 하는 편집은 이미지에서 해당 영역의 돌출부에 비례하여 $\lambda$를 사용해야 한다.

Experiments

1. Properties of LEDITS++

다음은 diffusion 기반 이미지 편집 기술의 주요 속성을 비교한 표이다.

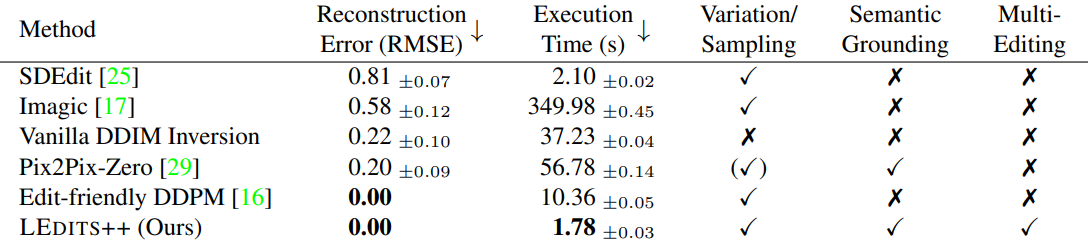
다음은 diffusion 기반 이미지 편집 방법들과 결과를 비교한 것이다.

다음은 SD 1.5를 사용하여 단 25 diffusion step으로 편집한 결과와 마스크들이다.

2. Semantically Grounded Image Editing

다음은 COCO panoptic segmentation에 대하여 IoU를 계산하여 semantic segmentation 품질을 측정한 그래프이다.

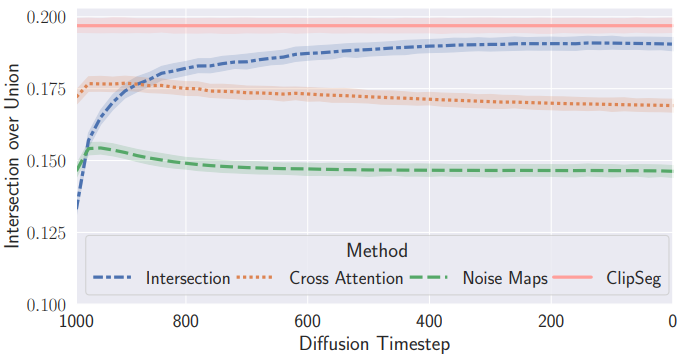
교집합 마스크가 다른 마스크보다 성능이 큰 차이로 우수하며 래퍼런스인 CLIPSeg와 비슷하다.

3. Image Editing Evaluation

다음은 여러 편집 방법들에 대해 명령 일치도(CLIP score)와 이미지 유사도(LPIPS score) 사이의 trade-off를 비교한 그래프이다.

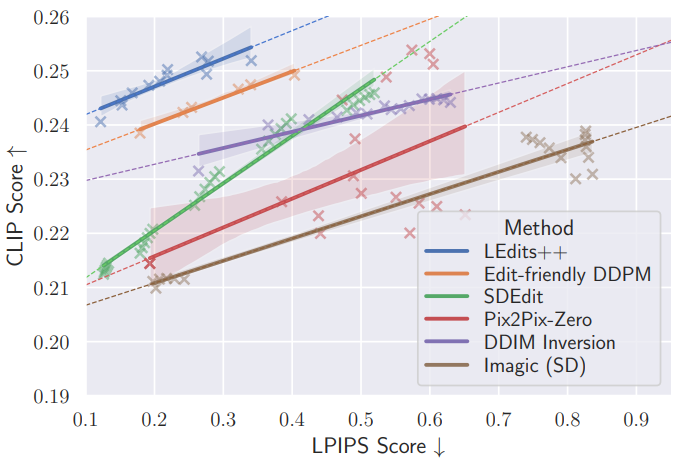
다음은 TEdBench에서의 편집 결과이다.

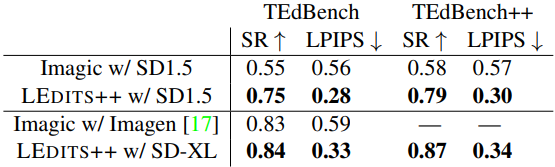
다음은 원래 TedBench와 수정된 버전(TEdBench++)의 성공률(SR)과 LPIPS 점수를 Imagic과 비교한 표이다.