[논문리뷰] LDMVFI: Video Frame Interpolation with Latent Diffusion Models

AAAI 2024. [Paper] [Github]
Duolikun Danier, Fan Zhang, David Bull
University of Bristol
13 Mar 2023

Introduction

동영상 프레임 보간(video frame interpolation, VFI)의 목적은 동영상 시퀀스에서 기존의 두 연속 프레임 사이에 중간 프레임을 생성하는 것이다. 예를 들어 슬로우 모션 콘텐츠를 생성하기 위해 일반적으로 프레임 속도를 종합적으로 높이는 데 사용된다. VFI는 동영상 압축, 새로운 view 합성, 의료 영상, 애니메이션 제작에도 사용되었다.

기존 VFI 방법은 대부분 심층 신경망을 기반으로 한다. 이러한 심층 모델은 아키텍처 설계 및 모션 모델링 접근 방식이 다르지만 출력과 ground-truth 중간 프레임 사이의 L1/L2 거리를 최소화하도록 학습된다는 점에서 주로 PSNR 지향적이다. 일부 이전 연구들에서는 PSNR 지향 모델을 fine-tuning하기 위해 feature distortion 기반 또는 GAN 기반 loss를 사용했지만 최적화 목적 함수에 대한 주요 기여는 여전히 L1/L2 기반 distortion loss이다. 결과적으로 기존 방법은 높은 PSNR 값을 달성하지만 특히 대규모 모션 및 동적 텍스처를 포함한 까다로운 시나리오에서 지각적으로 성능이 저하되는 경향이 있다.

대조적으로 diffusion model은 최근 사실적이고 지각적으로 최적화된 이미지와 동영상을 생성하는 데 놀라운 성능을 보여주었다. Diffusion model은 GAN이나 VAE를 포함한 다른 생성 모델을 능가하는 것으로 알려져 있다. 그러나 높은 충실도의 시각적 콘텐츠를 합성하는 강력한 능력에도 불구하고 VFI용 diffusion model의 적용과 현재의 PSNR 지향 VFI 접근 방식에 비해 잠재적인 이점은 완전히 조사되지 않았다.

본 논문에서는 조건부 이미지 생성 문제로 VFI를 공식화하는 VFI를 위한 latent diffusion model인 LDMVFI를 개발하였다. 특히 최근에 제안된 latent diffusion model (LDM)을 latent space에 이미지를 project하는 autoencoding model과 해당 latent space에서 reverse process를 수행하는 denoising U-Net으로 구성된 프레임워크 내에서 채택한다. LDM을 VFI에 더 잘 적응시키기 위해 VFI 특정 구성 요소, 특히 새로운 vector quantization (VQ) 기반 VFI autoencoding model인 VQ-FIGAN을 고안하여 기존 LDM보다 우수한 성능을 보여준다.

본 논문은 LDM을 사용하여 조건부 생성 문제로 VFI를 해결하려는 첫 번째 시도이자 최신 기술에 대한 diffusion 기반 VFI의 지각적 우월성을 입증한 첫 번째 시도이다.

Proposed Method: LDMVFI

동영상에서 두 개의 연속 프레임 $I^0$, $I^1$이 주어지면 VFI는 존재하지 않는 중간 프레임 $I^n$을 생성하는 것을 목표로 한다. 여기서 $n = 0.5$는 $\times 2$ 업샘플링을 위한 것이다. 생성적 관점에서 VFI에 접근할 때, 데이터셋 \(D = \{I_s^0 s, I_s^n, I_s^1 \}_{s=1}^S\)을 사용하여 조건부 분포 $p(I^n \vert I^0, I^1)$의 파라미터 근사를 학습하는 것이 목표이다. 이를 위해 LDM을 사용하여 VFI에 대한 조건부 생성을 수행한다. 제안된 LDMVFI는 두 가지 주요 구성 요소를 포함한다.

1. 프레임을 latent space에 project하고 latent 인코딩에서 타겟 프레임을 재구성하는 VFI용 autoencoding model인 VQ-FIGAN
2. 조건부 이미지 생성을 위해 latent space에서 reverse process를 수행하는 denoising U-Net

아래 그림은 LDMVFI의 개요를 보여준다.

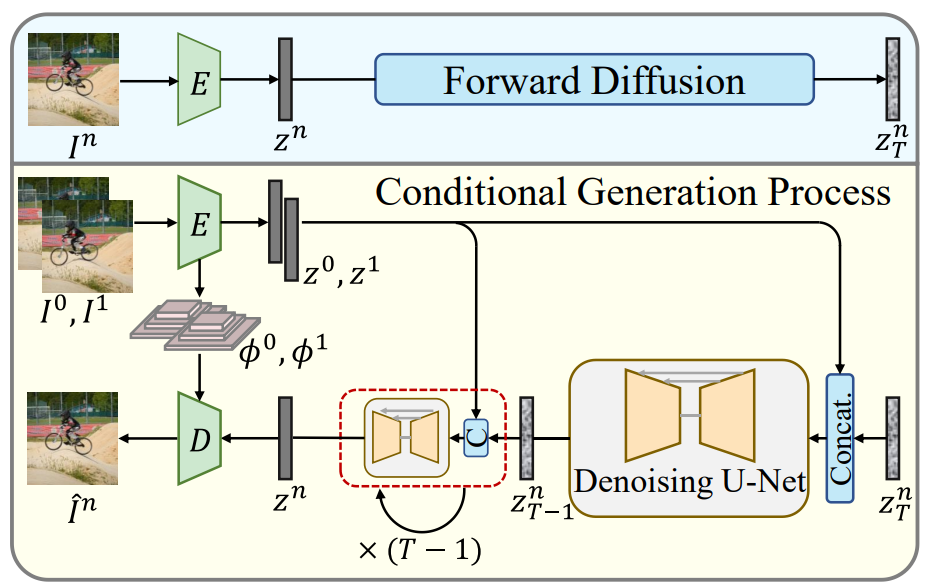
1. Latent Diffusion Models

LDM은 미리 정의된 Markov chain의 역방향 조건부 확률 분포를 학습하여 데이터 분포 $p(x)$를 근사화하는 생성 모델 클래스인 DDPM을 기반으로 한다. Diffusion model은 forward process와 reverse process의 두 가지 프로세스로 구성된다.

“깨끗한” 이미지 $x_0$에서 시작하여 noise schedule \(\{\beta_t\}_{t=1}^T\)에 따라 점진적으로 $x_0$에 Gaussian noise를 추가하는 길이 $T$의 Markov chain $q$를 다음과 같이 정의할 수 있다.

\[\begin{equation} q(x_t \vert x_{t-1}) = \mathcal{N}(x_t; \sqrt{1 - \beta_t} x_{t-1} \beta_t I) \end{equation}\]

여기서 noise scheudle \(\{\beta_t\}_{t=1}^T\)는 forward process가 완료되면 이미지의 마지막 상태가 순수한 Gaussian noise에 가까워지도록 설계된다.

\[\begin{equation} q(x_T \vert x_0) \approx \mathcal{N} (x_T; 0, I) \end{equation}\]

위의 Markov chain의 역과정 $q(x_{t−1} \vert x_t)$는 다루기 어렵기 때문에 이미지를 샘플링하기 위해 $\theta$로 parameterize된

\[\begin{equation} p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \sigma_t^2 I) \end{equation}\]

를 사용하여 이러한 역방향 조건부 확률을 근사화한다. 여기서 $\sigma_t^2$은 $\beta_t$를 기반한 값이고, $\mu_\theta$는 신경망으로 구현된다. 그런 다음 unconditional한 생성을 하기 위해 Gaussian noise $x_T \sim \mathcal{N} (x_T; 0,I)$에서 시작하여 $x_0$까지 이미지를 $p_\theta (x_{t-1} \vert x_t)$로 샘플링할 수 있다. 평균 $\mu_\theta (x_t, t)$를 예측하는 방법을 학습하는 대신 noise $\epsilon_\theta (x_t, t)$를 예측하도록 신경망을 학습할 수 있다.

\[\begin{equation} \mathcal{L}_\textrm{DM} = \mathbb{E}_{x_0, \epsilon \sim \mathcal{N}(0,I), t \sim \mathcal{U}(1, T)} [\| \epsilon - \epsilon_\theta (x_t, t) \|^2] \end{equation}\]

여기서 $x_t$는 forward process에서 샘플링되고 $\mathcal{U}(1, T)$는 \(\{1, 2, \cdots, T\}\)에서의 균등 분포이다. \(\mathcal{L}_\textrm{DM}\)은 log-likelihood $\log p_\theta (x_0)$에 대한 VLB의 재가중 변형에 해당한다.

조건부 생성 설정에서 조건부 reverse process $p_\theta(x_{t-1} \vert x_t, y)$를 근사화할 수 있다. 여기서 조건 $y$는 VFI에서 두 개의 입력 프레임을 나타낼 수 있다. 따라서 noise 예측 네트워크 $\epsilon_\theta (x_t, t, y)$는 reverse process에서 샘플링하기 위해 학습될 수 있다.

LDM에는 이미지 $x$를 저차원 latent 표현 $z$로 인코딩하는 이미지 인코더 $E: x \mapsto z$와 이미지 $x$를 재구성하는 디코더 $D: z \mapsto x$가 포함된다. Forward process와 reverse process는 latent space에서 발생하며 reverse process를 학습하기 위한 목적 함수는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{LDM} = \mathbb{E}_{E (x_0), \epsilon \sim \mathcal{N}(0,I), t \sim \mathcal{U}(1, T)} [\| \epsilon - \epsilon_\theta (z_t, t) \|^2] \end{equation}\]

이미지를 압축된 latent space에 project함으로써 LDM은 diffusion process가 데이터의 의미론적으로 중요한 부분에 집중할 수 있도록 하고 보다 계산적으로 효율적인 샘플링 프로세스를 가능하게 한다.

2. Autoencoding with VQ-FIGAN

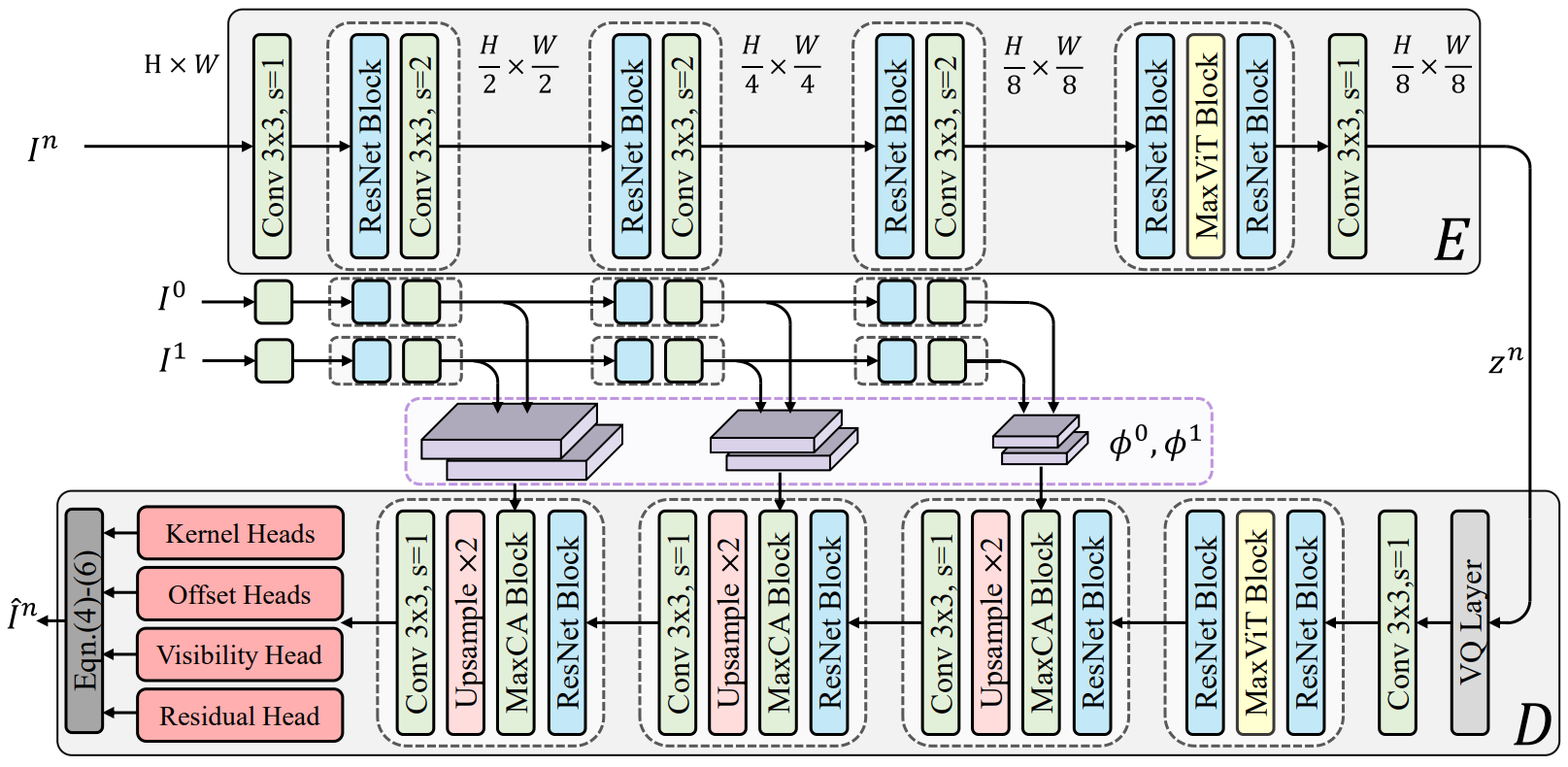
LDM의 원래 형태에서 autoencoding model \(\{E, D\}\)는 perceptual image codec으로 간주된다. 설계 목적은 인코딩 중에 고주파 디테일이 제거되고 디코딩에서 복구되는 효율적인 latent 표현으로 이미지를 project하는 것이다. 그러나 VFI의 맥락에서 이러한 정보는 보간된 동영상의 품질에 영향을 미칠 수 있으므로 디코더의 제한된 재구성 능력은 VFI 성능에 부정적인 영향을 미칠 수 있다. 본 논문은 고주파 디테일을 향상시키기 위해 위 그림에 나와 있는 VFI용 autoencoding model인 VQ-FIGAN을 제안한다. Backbone model은 LDM에서 사용된 원래 VQGAN과 유사하지만 세 가지 주요 차이점이 있다.

첫째, 프레임 지원 디코더를 설계하기 위해 inference 중에 인접 프레임을 사용할 수 있다는 VFI의 속성을 활용한다. 구체적으로, ground-truth 타겟 프레임 $I^n \in \mathbb{R}^{H \times W \times 3}$이 주어지면 인코더 $E$는 latent 인코딩 $z^n = E(I^n)$을 생성한다. 여기서 $z^n \in \mathbb{R}^{H/f \times W/f \times 3}$이고 $f$는 hyperparameter이다.

그런 다음, 디코더 $D$는 재구성된 프레임 $\hat{I}^n$을 출력하고, 입력 $z^n$뿐만 아니라 두 개의 이웃 프레임 $I^0$, $I^1$에서 $E$에 의해 추출된 feature 피라미드 $\phi^0$, $\phi^1$을 취한다. 디코딩하는 동안 이러한 feature 피라미드는 MaxViT 기반 Cross Attention 블록인 MaxCA 블록을 사용하여 여러 레이러에서 $z^n$의 디코딩된 feature와 융합된다. 여기서 attention 메커니즘에 대한 query 임베딩은 $z^n$의 디코딩된 feature를 사용하여 생성되고, key와 value 임베딩은 $\phi^0$, $\phi^1$에서 얻는다.

둘째, 원본 VQGAN은 특히 이미지 해상도가 높을 때 계산이 무겁고 (제곱에 비례) 메모리 집약적일 수 있는 ViT에서와 같이 완전한 self-attention을 사용한다. 고해상도 동영상에 대한 보다 효율적인 inference를 위해 MaxViT 블록을 사용하여 self-attention을 수행한다. MaxViT 블록의 multi-axis self-attention layer는 입력 크기와 관련하여 선형 복잡도를 달성하면서 로컬한 연산과 글로벌한 연산을 모두 수행하기 위해 windowed attention과 dilated grid attention을 결합한다.

셋째, 디코더가 재구성된 이미지를 직접 출력하는 대신 VQ-FIGAN은 VFI 성능을 향상시키기 위해 deformable convolution 기반 interpolation kernel을 출력한다. 구체적으로, $H$와 $W$가 프레임 높이와 너비인 경우 디코더 네트워크의 출력에는 크기 $K \times K$의 locally adaptive deformable convolution kernel의 파라미터

\[\begin{equation} \{ W_\tau, \alpha_\tau, \beta_\tau \} \end{equation}\]

가 포함된다. 여기서 $\tau = 0, 1$은 입력 프레임의 인덱스이다.

$W \in [0, 1]^{H \times W \times K \times K}$는 커널의 가중치를 포함하고 $\alpha, \beta \in \mathbb{R}^{H \times W \times K \times K}$는 커널의 공간 offset이다. 또한 디코더는 visibility map $v \in [0, 1]^{H \times W}$를 출력하고, VFI 성능을 더욱 향상시키기 위해 residual map $\delta \in \mathbb{R}^{H \times W}$를 출력한다. 보간된 프레임을 생성하기 위해 먼저 각 입력 프레임 $${I^\tau}_{\tau = 0,1}$에 대해 locally adaptive deformable convolution kernel이 수행된다.

\[\begin{equation} I^{n \tau} (h, w) = \sum_{i=1}^K \sum_{j=1}^K W_{h, w}^\tau (i, j) \cdot P_{h, w}^\tau (i, j) \\ P_{h, w}^\tau (i, j) = I^\tau (h + \alpha_{h, w}^\tau (i, j), w + \beta_{h, w}^\tau (i, j)) \end{equation}\]

여기서 $I^{n \tau}$는 $I^\tau$에서 얻은 결과를 나타내고 $P_{h, w}^\tau$는 출력 위치 $(h, w)$에 대해 $I^\tau$에서 샘플링된 패치이다. 이러한 중간 결과는 visibility map과 residual map을 사용하여 결합된다.

\[\begin{equation} \hat{I}^n = v \cdot I^{n0} + (1 - v) \cdot I^{n1} + \delta \end{equation}\]

VFI 성능을 유지하면서 메모리 요구 사항을 줄이기 위해 커널의 separability 속성을 이용하는 separable deformable convolution을 채택한다.

Training

Loss function이 LPIPS 기반 perceptual loss, 패치 기반 adversarial loss, VQ layer 기반 latent regularization 항으로 구성된 VQGAN의 원래 학습 설정을 따른다.

3. Conditional Generation with LDM

학습된 VQ-FIGAN을 사용하면 컴팩트한 latent space에 엑세스할 수 있다. 이를 위해 diffusion model의 noise 예측 parameterization을 채택하고 조건부 log-likelihood $\log p_\theta (z^n \vert z^0, z^1)$에서 재가중된 VLB를 최소화하여 denoising U-Net을 학습한다. 여기서 $z^0$, $z^1$는 두 입력 프레임의 latent 인코딩이다.

Training

구체적으로, denoising U-Net $\epsilon_\theta$는 타겟 프레임 $I^n$의 noisy한 latent 인코딩 $z_t^n$와 timestep $t$를 입력으로 취한다. 또한 입력 프레임 $I^0$, $I^1$에 대한 $z^0$, $z^1$도 입력으로 취한다. 다음을 최소화하여 각 timestep $t$에서 $z^n$에 추가되는 noise를 예측하도록 학습된다.

\[\begin{equation} \mathcal{L} = \mathbb{E}_{z^n, z^0, z^1, \epsilon \sim \mathcal{N}(0,I), t} [\| \epsilon - \epsilon_\theta (z_t^n, t, z^0, z^1) \|^2] \end{equation}\]

$\epsilon_\theta$의 학습 절차는 Algorithm 1에 요약되어 있다.

Inference

Inference 과정은 Algorithm 2에 요약되어 있다.

Network Architecture

$\epsilon_\theta$에 대해 시간으로 컨디셔닝된 U-Net을 사용하며, 모든 self-attention 블록은 계산 효율성을 위해 앞서 언급한 MaxViT 블록으로 대체된다. U-Net의 컨디셔닝 메커니즘은 입력에서 $z_t^n$와 $z^0$, $z^1$의 간단한 concatenation이다.

Experiments

• 학습 데이터셋: BVI-DVC, Vimeo90k
• Implementation Detail
  • VQ-FIGAN
    • Optimizer: Adam
    • learning rate: $10^{-5}$
    • 70 epoch
  • Denoising U-Net
    • Optimizer: Adam-W
    • learning rate: $10^{-6}$
    • 60 epoch

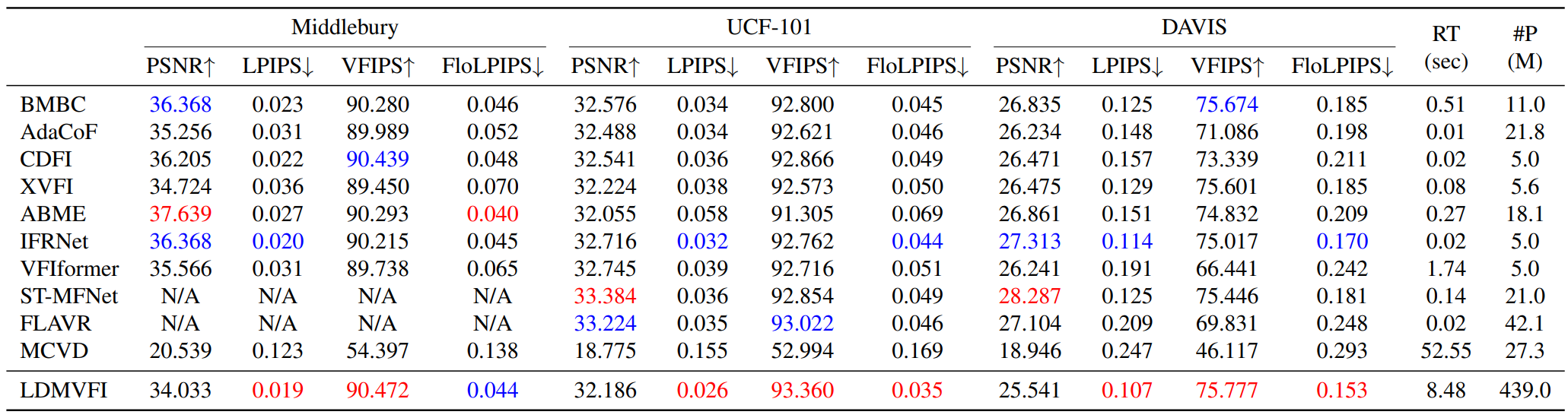
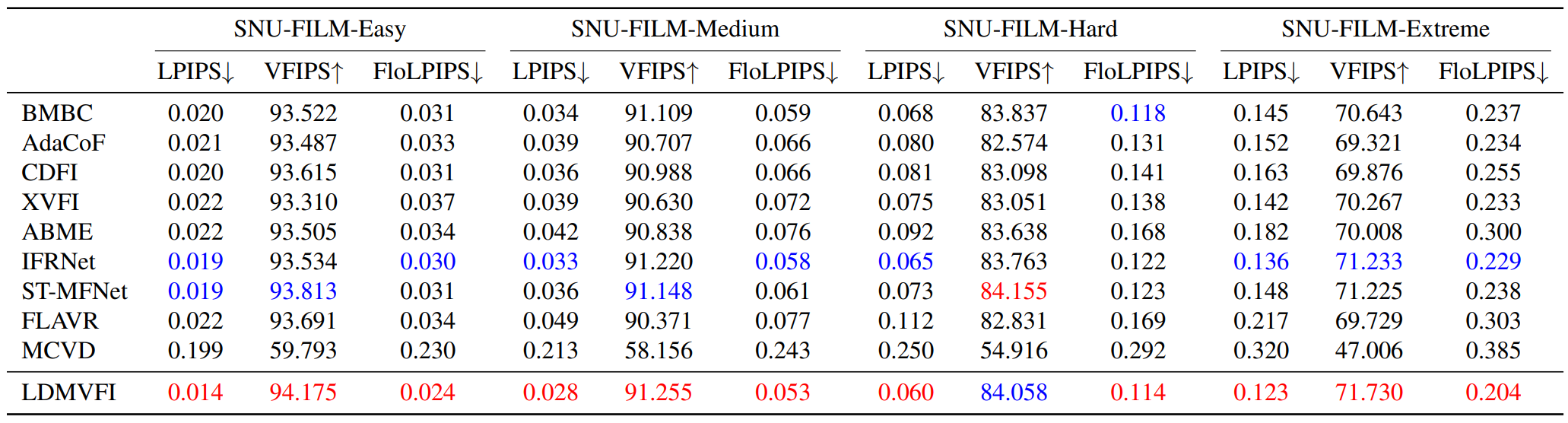
1. Quantitative Evaluation

다음은 LDMVFI를 다른 10가지 방법들과 정량적으로 비교한 표이다.

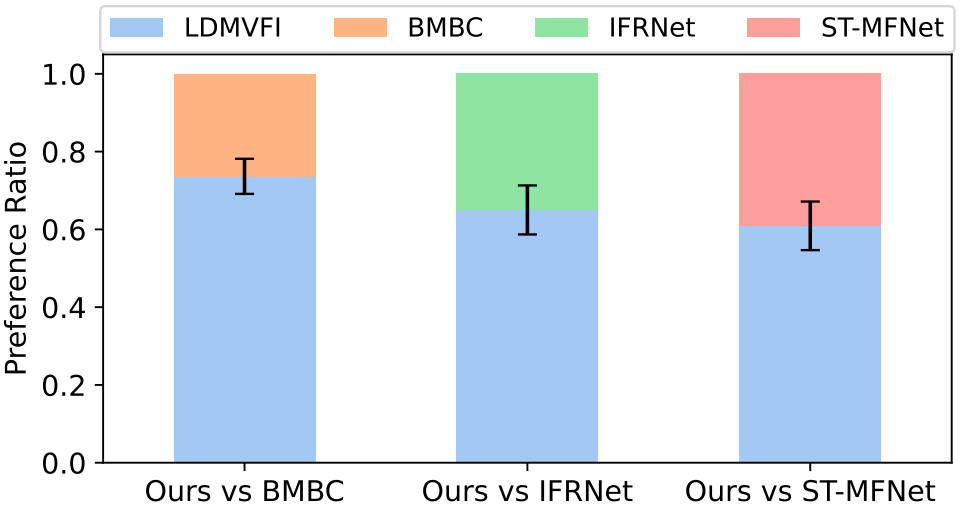
2. Subjective Experiment

다음은 선호도 비율에 대한 user study 결과이다.

3. Ablation Study

저자들은 다음 4가지 항목에 대한 ablation study를 진행하였다.

1. Sampling factor $f$
2. 채널 크기 $c$
3. Autoencoding model의 아키텍처
4. 컨디셔닝 메커니즘