[논문리뷰] LCM-LoRA: A Universal Stable-Diffusion Acceleration Module
arXiv 2023. [Paper] [Github]
Simian Luo, Yiqin Tan, Suraj Patil, Daniel Gu, Patrick von Platen, Apolinário Passos, Longbo Huang, Jian Li, Hang Zhao
Tsinghua University | Hugging Face
9 Nov 2023
Introduction
Latent Diffusion Model (LDM)은 텍스트나 스케치와 같은 다양한 입력에서 매우 상세하고 창의적인 이미지를 생성하는 데 중추적인 역할을 해왔다. 그럼에도 불구하고 LDM 고유의 느린 샘플링 프로세스는 실시간 적용을 방해하여 사용자 경험을 저하시킨다.
LDM을 가속화하려는 노력은 일반적으로 두 가지 범주로 나뉜다. 첫 번째 전략은 생성 프로세스를 가속화하기 위해 DDIM, DPMSolver, DPM-Solver++와 같은 고급 ODE-Solver를 사용하는 것이다. 두 번째 전략은 LDM을 증류(distillation)하는 것이다. ODE-Solver 방법은 필요한 inference step 수를 줄임에도 불구하고 특히 classifier-free guidance를 통합할 때 여전히 상당한 계산을 요구한다. 한편, Guided-Distill과 같은 distillation 방법은 유망하지만 높은 계산량으로 인해 실질적인 한계에 직면하였다. LDM으로 생성된 이미지의 속도와 품질 사이의 균형을 찾는 일은 계속해서 어려운 과제이다.
최근 느린 샘플링 문제에 대한 솔루션으로 Consistency Model (CM)에서 영감을 받은 Latent Consistency Model (LCM)이 등장했다. LCM은 reverse process를 augmented probability flow ODE (PF-ODE) 문제로 처리하여 접근하였다. 수치적 ODE-Solver를 통해 반복의 필요성을 없애 latent space의 해를 혁신적으로 예측한다. 그 결과 단 1~4개의 inference step만으로 고해상도 이미지를 매우 효율적으로 합성할 수 있다. 또한 LCM은 distillation 효율성 측면에서 탁월하여 최소 step inference를 위해 A100 GPU 1개로 단 32시간의 학습만이 필요하다.
이를 바탕으로 teacher diffusion model에서 시작하지 않고 사전 학습된 LCM을 fine-tuning하는 Latent Consistency Finetuning (LCF)이 개발되었다. 애니메이션, 실사 이미지, 판타지 이미지와 같은 특수한 데이터셋의 경우 Latent Consistency Distillation (LCD)를 사용하여 사전 학습된 LDM을 LCM으로 증류하거나 LCF를 사용하여 LCM을 직접 fine-tuning하는 등의 추가 단계가 필요하다. 그러나 이러한 추가 학습은 다양한 데이터셋에 걸쳐 LCM을 빠르게 적용하는 데 장애가 될 수 있으며, 임의의 데이터셋에 대한 학습 없는 빠른 inference가 어렵다.
본 논문은 이 문제를 해결하기 위해 다양한 Stable-Diffusion (SD)을 fine-tuning한 모델 또는 SD LoRA에 직접 연결하여 최소한의 step으로 빠른 inference를 지원할 수 있으며 범용 학습이 필요 없는 가속 모듈인 LCM-LoRA를 도입하였다. DDIM, DPM-Solver, DPM-Solver++와 같은 이전 수치적 PF-ODE solver와 비교하여 LCM-LoRA는 신경망 기반 PF-ODE solver 모듈의 새로운 클래스이다. LCM-LoRA는 fine-tuning된 다양한 SD 모델과 LoRA 전반에 걸쳐 강력한 일반화 능력을 보여준다.
LCM-LoRA
1. LoRA Distillation for LCM
LCM은 사전 학습된 오토인코더의 latent space를 활용하여 guided diffusion model을 LCM으로 증류하는 1단계 guided distillation을 사용하여 학습된다. 이 프로세스에는 생성된 샘플이 고품질 이미지를 생성하는 궤적을 따르도록 보장하는 augmented PF-ODE를 해결하는 과정이 포함된다. Distillation은 필요한 샘플링 step 수를 크게 줄이면서 궤적의 충실도를 유지하는 데 중점을 둔다. 이 방법에는 수렴 속도를 높이는 Skipping-Steps 기술 등이 포함되어 있다. LCD의 pseudo-code는 Algorithm 1과 같다.

LCM의 distillation 프로세스는 사전 학습된 diffusion model의 파라미터 위에 수행되므로 LCD를 diffusion model의 fine-tuning 프로세스로 간주할 수 있다. 이를 통해 Low-Rank Adaptation와 같은 파라미터 효율적인 fine-tuning 방법을 사용할 수 있다. LoRA는 low-rank decomposition을 적용하여 사전 학습된 가중치 행렬을 업데이트한다. 가중치 행렬 $W_0 \in \mathbb{R}^{d \times k}$가 주어지면 업데이트는
로 표현된다. 학습 중에 $W_0$는 일정하게 유지되고 기울기 업데이트는 $A$와 $B$에만 적용된다. 입력 $x$에 대한 수정된 forward pass는 다음과 같다.
\[\begin{equation} h = W_0 x + \Delta W x = W_0 x + BAx \end{equation}\]이 식에서 $h$는 출력 벡터이며, $W_0$와 $\Delta W = BA$의 출력은 입력 $x$를 곱한 후 더해진다. 전체 파라미터 행렬을 두 개의 하위 행렬의 곱으로 분해함으로써 LoRA는 학습 가능한 파라미터 수를 크게 줄여 메모리 사용량을 줄인다.

위 표는 LoRA를 사용할 때 전체 모델의 총 파라미터 수를 학습 가능한 파라미터 수와 비교한 것이다. LCM distillation 프로세스 중에 LoRA를 통합하면 학습 가능한 파라미터의 수가 크게 줄어들어 학습에 필요한 메모리 요구 사항이 효과적으로 감소한다.
LCM 논문에서는 SD-V1.5와 SD-V2.1과 같은 기본 SD 모델을 주로 증류했다. 본 논문은 이 distillation 프로세스를 향상된 text-to-image 능력과 더 많은 파라미터 수를 갖춘 보다 강력한 모델(ex. SDXL, SSD-1B)로 확장했다. 본 논문의 실험은 LCD 패러다임이 더 큰 모델에도 잘 적응한다는 것을 보여준다. 다양한 모델에서 생성된 결과는 아래 그림과 같다. (classifier-free guidance scale $\omega = 7.5$)

2. LCM-LoRA as Universal Acceleratiion Module
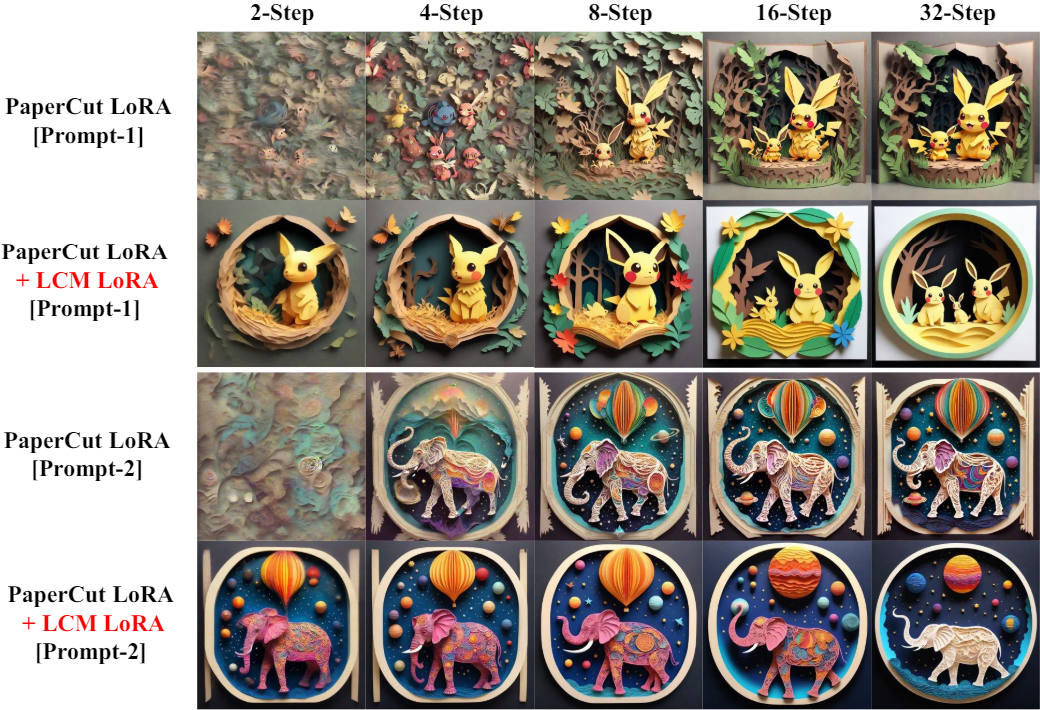
LoRA를 기반으로 하면 메모리 요구 사항을 크게 줄이면서 사전 학습된 모델을 fine-tuning할 수 있다. LoRA 프레임워크 내에서 결과 LoRA 파라미터는 원래 모델 파라미터에 매끄럽게 통합될 수 있다. 한편, 특정 task에 맞게 특정 데이터셋에서 fine-tuning할 수 있다. 저자들은 LCM-LoRA 파라미터가 특정 스타일의 데이터셋에서 fine-tuning된 다른 LoRA 파라미터와 직접 결합될 수 있음을 발견했다. 이러한 결합을 통해 추가 학습 없이 최소한의 샘플링 step으로 특정 스타일의 이미지를 생성할 수 있는 모델이 생성된다.
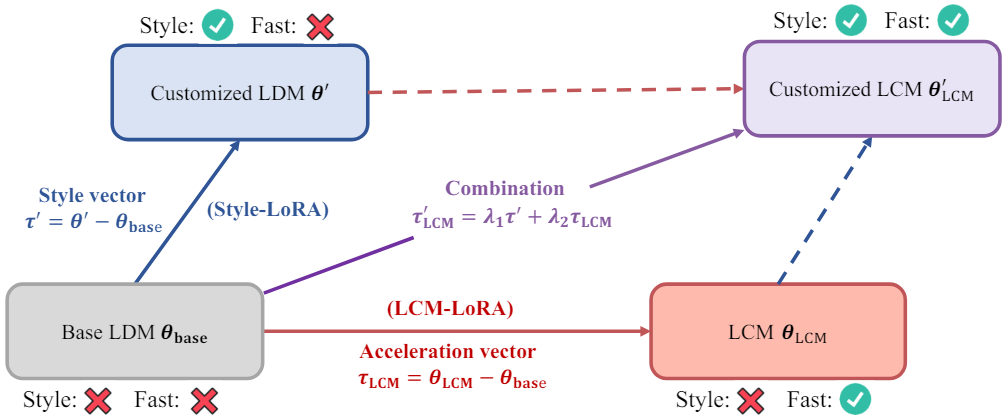
위 그림과 같이 LCM-LoRA 파라미터 \(\tau_\textrm{LCM}\)를 “가속 벡터”라고 하며, 맞춤형 데이터셋에서 fine-tuning된 LoRA 파라미터 $\tau^\prime$은 “스타일 벡터”라 한다. 그러면 맞춤형 이미지를 생성하는 LCM은 다음과 같이 가속 벡터와 스타일 벡터의 선형 결합으로 얻을 수 있다.
여기서 $\lambda_1$과 $\lambda_2$는 hyperparameter이다. 특정 스타일의 LoRA 파라미터와 LCM-LoRA 파라미터와의 결합의 생성 결과는 아래 그림과 같다. 결합된 파라미터에 대한 추가 학습은 수행되지 않았다.