[논문리뷰] Latent Consistency Models: Synthesizing High-Resolution Images with Few-Step Inference (LCM)
arXiv 2023. [Paper] [Page] [Github]
Simian Luo, Yiqin Tan, Longbo Huang, Jian Li, Hang Zhao
Tsinghua University
6 Oct 2023

Introduction
Diffusion model은 다양한 도메인에서 상당한 주목을 받고 놀라운 결과를 달성한 강력한 생성 모델로 등장했다. 특히, latent diffusion model (LDM) (ex. Stable Diffusion)은 특히 고해상도 text-to-image 합성 task에서 탁월한 성능을 보여주었다. LDM은 샘플의 점진적인 denoising을 수행하는 반복적인 reverse process를 활용하여 텍스트 설명에 따라 고품질 이미지를 생성할 수 있다.
그러나 diffusion model에는 눈에 띄는 단점이 있다. 반복적인 reverse process로 인해 생성 속도가 느려지고 실시간 적용성이 제한된다. 이러한 단점을 극복하기 위해 연구자들은 ODE solver를 향상하여 10~20 샘플링 step 내에서 이미지를 생성할 수 있도록 샘플링 속도를 향상시키는 여러 가지 방법을 제안했다. 또 다른 접근 방식은 사전 학습된 diffusion model을 few-step inference가 가능한 모델로 추출(distill)하는 것이다.
최근 생성 속도를 높이기 위한 유망한 대안으로 Consistency Model (CM)이 제안되었다. ODE 궤적에서 점 일관성을 유지하는 일관성 매핑을 학습함으로써 consistency model은 단일 step 생성을 허용하므로 계산 집약적인 반복이 필요하지 않다. 그러나 consistency model은 픽셀 공간 이미지 생성에만 국한되어 있어 고해상도 이미지를 합성하는 데 적합하지 않다. 또한 조건부 diffusion model에 대한 적용과 classifier-free guidance의 통합은 연구되지 않았으므로 해당 방법은 text-to-image 합성에 적합하지 않다.
본 논문에서는 빠른 고해상도 이미지 생성을 위한 Latent Consistency Model (LCM)을 소개한다. LDM을 미러링하여 Stable Diffusion의 사전 학습된 오토인코더의 이미지 latent space에 consistency model을 사용한다. 저자들은 증강된 PF-ODE를 해결하여 사전 학습된 guided diffusion model을 latent consistency model로 효율적으로 변환하는 1단계 guided distillation 방법을 제안하였다. 또한 사전 학습된 LCM을 fine-tuning하여 맞춤형 이미지 데이터셋에 대한 few-step inference를 지원하는 Latent Consistency Finetuning을 제안하였다.
Latent Consistency Models
1. Consistency Distillation in the Latent Space
Stable Diffusion (SD)과 같은 대규모 diffusion model에서 이미지 latent space를 활용하면 이미지 생성 품질이 효과적으로 향상되고 계산 부하가 줄어든다. SD에서 오토인코더 $(\mathcal{E}, \mathcal{D})$는 먼저 높은 차원의 이미지 데이터를 낮은 차원의 latent 벡터 $z = \mathcal{E}(x)$로 압축하도록 학습된 다음 이미지를 $\hat{x} = \mathcal{D}(z)$로 재구성하기 위해 디코딩된다. Latent space에서 diffusion model을 학습시키면 픽셀 기반 모델에 비해 계산 비용이 크게 줄어들고 inference 속도가 빨라진다. LDM을 사용하면 노트북 GPU에서 고해상도 이미지를 생성할 수 있다. LCM의 경우 CM에 사용되는 픽셀 공간과 대조적으로 consistency distillation을 위해 latent space의 이점을 활용한다. Latent Consistency Distillation (LCD)라고 하는 이 접근 방식은 사전 학습된 SD에 적용되어 1~4 step으로 고해상도 (ex. 768$\times$768) 이미지를 합성할 수 있다. 본 논문은 조건부 생성에 중점을 둔다. Reverse process의 PF-ODE는 다음과 같다.
\[\begin{equation} \frac{dz_t}{dt} = f(t) z_t + \frac{g^2 (t)}{2 \sigma_t} \epsilon_\theta (z_t, c, t), \quad z_T \sim \mathcal{N} (0, \tilde{\sigma}^2 I) \end{equation}\]여기서 $z_t$는 이미지 latent, $\epsilon_\theta (z_t, c, t)$는 noise 예측 모델, $c$는 주어진 조건(ex. 텍스트)이다. PF-ODE를 $T$에서 $0$으로 풀어 샘플을 뽑을 수 있다. LCD를 수행하기 위해 consistency function $f_\theta : (z_t, c, t) \mapsto z_0$를 도입하여 $t = 0$에서 PF-ODE의 해를 직접 예측한다. 다음과 같이 noise 예측 모델 \(\hat{\epsilon}_\theta\)로 $f_\theta$를 parameterize한다.
\[\begin{equation} f_\theta (z, c, t) = c_\textrm{skip} (t) z + c_\textrm{out} (t) \bigg( \frac{z - \sigma_t \hat{\epsilon}_\theta (z, c, t)}{\alpha_t} \bigg) \end{equation}\]여기서 $c_\textrm{skip} (0) = 1$이고 $c_\textrm{out} (0) = 0$이며, \(\hat{\epsilon}_\theta (z, c, t)\)는 teacher diffusion model과 같은 파라미터로 초기화된 noise 예측 모델이다. 특히, $f_\theta$는 teacher diffusion model의 parameterization에 따라 다양한 방식으로 parameterize될 수 있다.
저자들은 효율적인 ODE solver $\Psi (z_t, t, s, c)$가 시간 $t$에서 $s$까지 PF-ODE의 적분을 근사화하는 데 사용할 수 있다고 가정하였다. 실제로 $\Psi$로 DDIM, DPM-Solver, DPM-Solver++를 사용할 수 있다. Inference가 아닌 학습과 distillation에만 이러한 solver를 사용한다. LCM은 consistency distillation loss를 최소화하여 PF-ODE의 해를 예측하는 것을 목표로 한다.
\[\begin{equation} \mathcal{L}_\textrm{CD} (\theta, \theta^{-}; \Psi) = \mathbb{E}_{z, c, n} [d (f_\theta (z_{t_{n+1}}, c, t_{n+1}), f_{\theta^{-}} (\hat{z}_{t_n}^\Psi, c, t_n))] \end{equation}\]여기서 $\hat{z}{t_n}^\Psi$는 ODE solver $\Psi$를 사용하여 $t{n+1}$에서 $t_n$까지 PF-ODE의 진화를 추정한 것이다.
\[\begin{equation} \hat{z}_{t_n}^\Psi - z_{t_{n+1}} = \int_{t_{n+1}}^{t_n} \bigg( f(t) z_t + \frac{g^2 (t)}{2 \sigma_t} \epsilon_\theta (z_t, c, t) \bigg) dt \approx \Psi (z_{t_{n+1}}, t_{n+1}, t_n, c) \end{equation}\]여기서 solver $\Psi$는 $t_{n+1}$에서 $t_{n+1}$에서 $t_n$까지의 적분을 근사하기 위해 사용된다.
2. One-Stage Guided Distillation by solving augmented PF-ODE
Classifier-free guidance (CFG)는 Stable Diffusion에서 텍스트에 맞는 고품질 이미지를 합성하는 데 중요하며 일반적으로 6 이상의 CFG scale $\omega$가 필요하다. 따라서 CFG를 distillation 방법에 통합하는 것이 필수이다. Guided-Distill은 guided diffusion model에서 few-step 샘플링을 지원하기 위해 2단계 distillation을 도입했다. 그러나 계산 집약적이다 (2-step inference의 경우 최소 45 A100 GPU day). LCM은 2-step inference를 위해 단 32 A100 GPU hour 학습만 필요하다. 또한 2단계 guided distillation은 오차가 누적되어 최적이 아닌 성능으로 이어질 수 있다. 반면 LCM은 증강된 PF-ODE를 해결하여 효율적인 1단계 guided distillation을 채택한다.
Reverse process에 사용되는 CFG는 다음과 같다.
\[\begin{equation} \tilde{\epsilon}_\theta (z_t, \omega, c, t) := (1+\omega) \epsilon_\theta (z_t, c, t) - \omega \epsilon_\theta (z_t, \varnothing, t) \end{equation}\]여기서 원래의 noise 예측은 conditional noise과 unconditional noise의 선형 결합으로 대체되며 $\omega$는 guidance scale이다. 가이드된 reverse process에서 샘플링하려면 다음과 같은 증강 PF-ODE를 풀어야 한다.
\[\begin{equation} \frac{dz_t}{dt} = f(t) z_t + \frac{g^2 (t)}{2 \sigma_t} \tilde{\epsilon}_\theta (z_t, \omega, c, t), \quad z_T \sim \mathcal{N} (0, \tilde{\sigma}^2 I) \end{equation}\]1단계 guided distillation을 효율적으로 수행하기 위해 저자들은 $t = 0$에 대한 증강된 PF-ODE의 해를 직접 예측하기 위해 증강된 consistency function $f_\theta: (z_t, \omega, c, t) \mapsto z_0$를 도입하였다. \(\hat{\epsilon}_\theta (z, c, t)\)가 \(\hat{\epsilon}_\theta (z, \omega, c, t)\)로 대체된다는 점을 제외하고 동일한 방식으로 $f_\theta$를 parameterize한다. Consistency loss는 증강된 consistency function $f_\theta (z_t, \omega, c, t)$를 사용한다는 점을 제외하면 동일하다.
\[\begin{equation} \mathcal{L}_\textrm{CD} (\theta, \theta^{-}; \Psi) = \mathbb{E}_{z, c, \omega n} [d (f_\theta (z_{t_{n+1}}, \omega, c, t_{n+1}), f_{\theta^{-}} (\hat{z}_{t_n}^{\Psi, \omega}, \omega, c, t_n))] \end{equation}\]$\omega$와 $n$은 각각 \([\omega_\textrm{min}, \omega_\textrm{max}]\)와 \(\{1, \ldots, N−1\}\)에서 균일하게 샘플링된다. \(\hat{z}_{t_n}^{\Psi, \omega}\)는 다음과 같이 새로운 noise 모델 \(\hat{\epsilon}_\theta (z_t, \omega, c, t)\)를 사용하여 추정된다.
\[\begin{aligned} \hat{z}_{t_n}^{\Psi, \omega} - z_{t_{n+1}} &= \int_{t_{n+1}}^{t_n} \bigg( f(t) z_t + \frac{g^2 (t)}{2 \sigma_t} \tilde{\epsilon}_\theta (z_t, \omega, c, t) \bigg) dt \\ &= (1 + \omega) \int_{t_{n+1}}^{t_n} \bigg( f(t) z_t + \frac{g^2 (t)}{2 \sigma_t} \epsilon_\theta (z_t, c, t) \bigg) dt - \omega \int_{t_{n+1}}^{t_n} \bigg( f(t) z_t + \frac{g^2 (t)}{2 \sigma_t} \epsilon_\theta (z_t, \varnothing, t) \bigg) dt \\ &\approx (1 + \omega) \Psi (z_{t_{n+1}}, t_{n+1}, t_n, c) - \omega \Psi (z_{t_{n+1}}, t_{n+1}, t_n, \varnothing) \end{aligned}\]마찬가지로 DDIM, DPM-Solver, DPM-Solver++를 PF-ODE solver $\Psi$로 사용할 수 있다.
3. Accelerating Distillation with Skipping Time Steps
이산적인 diffusion model은 일반적으로 고품질 생성 결과를 얻기 위해 긴 timestep schedule \(\{t_i\}_i\)를 사용하여 noise 예측 모델을 학습시킨다. 예를 들어 Stable Diffusion (SD)의 schedule 길이는 1,000이다. 그러나 이렇게 schedule이 길어지면 Latent Consistency Distillation (LCD)를 SD에 직접 적용하는 것은 문제가 될 수 있다. 모델은 1,000개의 timestep 전체에 걸쳐 샘플링해야 하며 consistency loss는 LCM 모델의 예측 $f_\theta (z_{t_{n+1}}, c, t_{n+1})$을 이후 step의 예측 $f_\theta (z_{t_n}, c, t_n)$와 정렬하려고 시도한다. $t_n − t_{n+1}$은 작기 때문에 $z_{t_n}$과 $z_{t_{n+1}}$은 이미 서로 가까워서 약간의 consistency loss가 발생한다. 따라서 수렴 속도가 느려진다. 이 문제를 해결하기 위해 저자들은 생성 품질을 유지하면서 빠른 수렴을 달성하기 위해 schedule의 길이를 상당히 단축하는 Skipping-Step 방법을 도입하였다.
Consistency model(CM)은 연속 시간 EDM schedule을 사용하고 Euler 또는 Heun Solver를 수치적 PF-ODE solver로 사용한다. LCM의 경우 Stable Diffusion의 이산적인 schedule에 적응하기 위해 DDIM, DPM-Solver, DPM-Solver++를 ODE solver로 사용한다. 이러한 고급 solver들은 PF-ODE를 효율적으로 풀 수 있다.
Skipping-Step 방법은 인접한 timestep $t_{n+1} \rightarrow t_n$의 일관성을 보장하는 대신 현재 timestep과 $k$ step 떨어진 $t_{n+k} \rightarrow t_n$의 일관성을 보장하는 것을 목표로 한다. $k = 1$로 설정하면 원래 schedule이 되어 수렴이 느려지고 $k$가 매우 크면 ODE solver의 큰 근사 오차가 발생할 수 있다. Skipping-Step 방식은 LCD를 가속화하는 데 매우 중요하다. 특히 consistency distillation loss는 $t_{n+k}$에서 $t_n$까지의 일관성을 보장하기 위해 다음과 같이 수정된다.
\[\begin{equation} \mathcal{L}_\textrm{CD} (\theta, \theta^{-}; \Psi) = \mathbb{E}_{z, c, \omega, n} [d (f_\theta (z_{t_{n+k}, \omega, c, t_{n+k}}), f_{\theta^{-}} (\hat{z}_{t_n}^{\Psi, \omega}, \omega, c, t_n))] \end{equation}\]\(\hat{z}_{t_n}^{\Psi, \omega}\)은 증강된 PF-ODE solver $\Psi$를 사용한 $z_{t_n}$의 추정값이다.
\[\begin{equation} \hat{z}_{t_n}^{\Psi, \omega} \leftarrow z_{t_{n+k}} + (1 + \omega) \Psi (z_{t_{n+k}}, t_{n+k}, t_n, c) - \omega \Psi (z_{t_{n+k}}, t_{n+k}, t_n, \varnothing) \end{equation}\]예를 들어 $t_{n+k}$에서 $t_n$까지의 DDIM PF-ODE solver \(\Psi_\textrm{DDIM}\)의 자세한 공식은 다음과 같다.
\[\begin{equation} \Psi_\textrm{DDIM} (z_{t_{n+k}}, t_{n+k}, t_n, c) = \frac{\alpha_{t_n}}{\alpha_{t_{n+k}}} z_{t_{n+k}} - \sigma_{t_n} \bigg( \frac{\sigma_{t_{n+k}} \cdot \alpha_{t_n}}{\alpha_{t_{n+k}} \cdot \sigma_{t_n}} - 1 \bigg) \hat{\epsilon}_\theta (z_{t_{n+k}}, c, t_{n+k}) - z_{t_{n+k}} \end{equation}\]CFG와 Skipping-Step 기술을 사용하는 LCD의 pseudo-code는 Algorithm 1과 같다. Consistency Distillation (CD) 알고리즘에서의 수정 사항은 파란색으로 강조 표시되어 있다.

4. Latent Consistency Fine-tuning for Customized Dataset
Stable Diffusion과 같은 생성 모델은 다양한 tex-to-image 생성 task에 탁월하지만 다운스트림 task의 요구 사항을 충족하기 위해 맞춤형 데이터셋을 fine-tuning해야 하는 경우가 많다. 본 논문은 사전 학습된 LCM을 위한 fine-tuning 방법인 Latent Consistency Fine-tuning (LCF)를 제안하였다. Consistency Training (CT)에서 영감을 받은 LCF는 해당 데이터에 대해 학습된 teacher diffusion model에 의존하지 않고도 맞춤형 데이터셋에 대해 효율적인 few-step inference를 가능하게 한다. 이 접근 방식은 diffusion model에 대한 기존의 fine-tuning 방법에 대한 실행 가능한 대안을 제시한다. LCF의 pseudo-code는 Algorithm 4와 같다.

Experiment
1. Text-to-Image Generation
- 데이터셋: LAION-Aesthetics-6+ (12M), LAION-Aesthetics-6.5+ (650K)
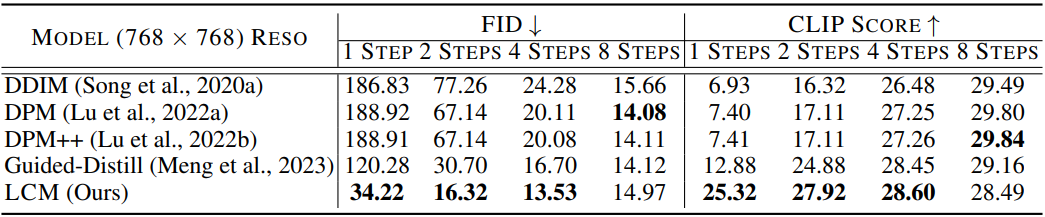
다음은 512$\times$512 해상도에서 CFG scale $\omega = 8$에 대한 정량적 결과를 비교한 표이다.
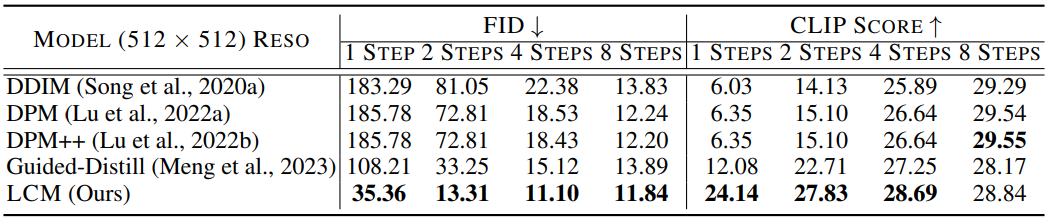
다음은 768$\times$768 해상도에서 CFG scale $\omega = 8$에 대한 정량적 결과를 비교한 표이다.
다음은 LAION-Aesthetic-6.5+에서의 text-to-image 생성 결과이다.

2. Ablation Study
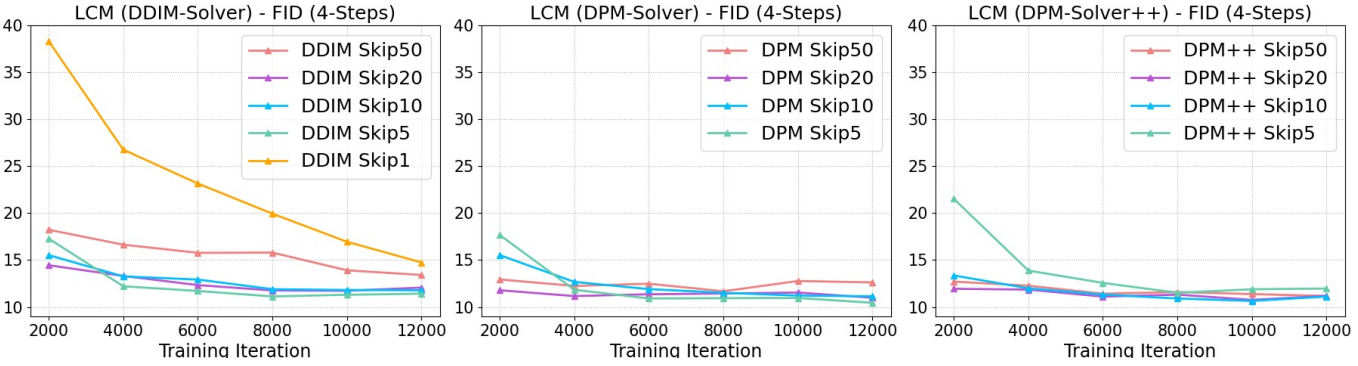
다음은 다양한 ODE solver와 skipping step $k$에 대한 ablation study 결과이다.
다음은 다양한 CFG scale $\omega$에 대한 ablation study 결과이다.
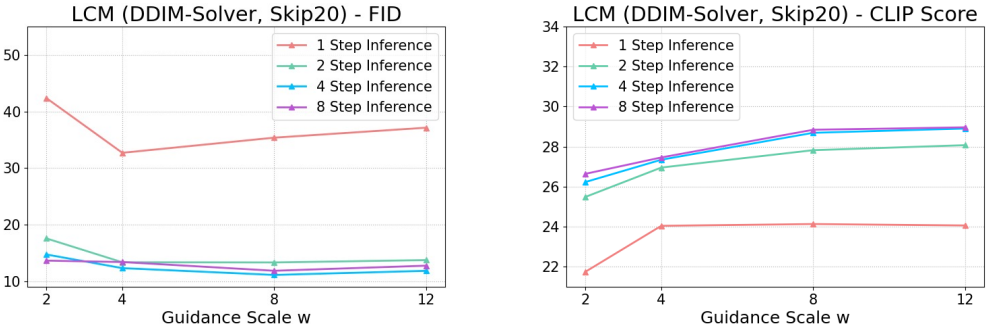
다음은 다양한 CFG scale $\omega$에 대한 4-step LCM의 결과이다.

3. Downstream Consistency Fine-tuning Results
다음은 포켓몬 데이터셋 (왼쪽)과 심슨 데이터셋 (오른쪽)에 대하여 LCF를 사용한 4-step LCM의 결과이다.
