[논문리뷰] Large Language Models to Diffusion Finetuning

ICML 2025. [Paper] [Github]
Edoardo Cetin, Tianyu Zhao, Yujin Tang
Sakana AI
27 Jan 2025

Introduction

LLM의 scalability는 현재 foundation model의 핵심 요소이지만, 언어 모델(LM)은 AGI에서 기대할 수 있는 여러 가지 귀중한 특성, 예를 들어 가장 중요한 의사 결정에 대한 연산량을 scaling하는 능력이 본질적으로 부족하다. 이러한 한계를 해결하기 위한 방법은 프롬프트나 타겟팅된 검색을 통해 더욱 섬세한 응답을 유도하고, 추론 과정을 생성된 토큰의 공간에 고정하는 데 집중하였다.

Diffusion model은 LM 패러다임을 보완하는 것으로 보이는 속성을 제공한다. 예를 들어, diffusion의 반복적인 특성은 생성된 출력의 길이와 관계없이 특정 task의 난이도나 사용자가 요구하는 모든 정확도 수준에 맞춰 컴퓨팅을 적응적으로 scaling할 수 있도록 한다. 그러나 이러한 유용한 속성에도 불구하고, 언어 학습을 위한 diffusion model은 현재 autoregressive 모델에 비해 상당히 뒤떨어져 있다.

본 논문에서는 LM to Diffusion (L2D)을 도입하여 두 프레임워크의 강점을 통합하는 것을 목표로 하였다. L2D는 사전 학습된 LM에 scaling 특성과 diffusion의 잠재력을 제공하는 새로운 fine-tuning 방법이다. Diffusion model을 처음부터 학습하는 대신, LM을 single-step diffusion으로 변환하여 autoregressive한 사전 학습 과정에서 효율적으로 획득한 방대한 이해를 활용한다. 그런 다음, 소량의 새로운 파라미터를 도입하여 모델에 새로운 다단계 추론 기술, 필요에 따라 계산을 scaling할 수 있는 능력, 그리고 강력한 guidance 기법을 통합할 수 있는 잠재력을 부여한다. 이 모든 것이 원래의 성능을 손상시키지 않으면서 가능하다.

Gaussian Diffusion for LM Finetuning

1. L2D Parametrization and Training Formulation

Diffusion model을 학습하기 위한 효과적인 loss 선택은 각 손상 수준에 포함된 부분 정보를 고려하여 손상되지 않은 타겟 데이터 포인트 $p_1$의 값을 예측하는 것이다. $p_1$이 continuous한 도메인에 대한 분포인 경우, 이는 일반적으로 DDPM 알고리즘에서 널리 사용되는 것처럼 모든 timestep $t$에 대해 단순한 MSE loss를 사용하여 수행된다.

\[\begin{equation} L^\textrm{L2} (\theta) = \mathbb{E}_{t, x_0, x_1} [\| x_1 - f_\theta (x_t, t) \|_2^2] \\ \textrm{where} \quad x_t = \alpha_t x_1 + \beta_t x_0, \quad x_0 \sim N (0, I) \end{equation}\]

Diffusion을 위한 또 다른 주요 디자인 결정은 $f_\theta$가 학습할 denoising process를 정의하는 schedule의 선택이다. 이는 학습 및 inference의 모든 측면에 영향을 미친다. 본 논문에서는 schedule로 다음과 같은 \(\alpha_t\)와 \(\beta_t\)를 사용한다.

\[\begin{equation} \alpha_t = t, \quad \beta_t = (1 - t) \sigma \end{equation}\]

($\sigma$는 모든 timestep에 대한 SNR을 선형적으로 조정하는 hyperparameter)

이 선택은 diffusion에 대한 바람직한 “직선화” 속성을 가지고 있는 것으로 나타났고 최근 널리 채택되는 rectified flow matching의 schedule과 밀접하게 연관되어 있다. $p_0 = N(0, \sigma^2 I)$로 설정하면, schedule이 \(\alpha_t = t\)와 \(\beta_t = 1 - t\)로 단순화된다.

Continuous한 경우와 달리 언어 모델링은 유한한 vocabulary $V$에 정의된 타겟 분포 $p_1$에 대해 작동한다. 여기서 각 인덱스 $y \in 1, \ldots, \vert V \vert$에는 토큰 임베딩 $x \in \mathbb{R}^d$가 대응한다. 이러한 주요 차이점은 언어 모델링에서 diffusion이 아직 우세한 레시피를 갖지 못한 주된 이유 중 하나이다.

본 논문에서는 일반적인 continuous diffusion에서와 같이 토큰 임베딩 $x$에 대한 diffusion을 선택했지만 MSE loss를 사용하지 않았다. 대신, 간단한 cross-entropy loss로 diffusion model을 학습시켜 기존의 single-step 언어 모델링과 직접 연결한다. 타겟 데이터 분포 $p_1$에서 샘플링된 레이블 $y$로 인덱싱된 토큰 $x_1$과 이전 토큰 $c$의 컨텍스트가 주어지면, diffusion loss는 다음과 같다.

\[\begin{equation} L^\textrm{CE} = - \mathbb{E}_{x_0, x_1, t} [\log (f_\theta (x_t, t, c)_y)], \quad \textrm{where} \\ x_0 \sim \mathcal{N}(0, \sigma^2 I), \quad x_1 = V_y \sim p_1 \\ t \sim \mathcal{U}[0, 1], \quad x_t = t x_1 + (1 - t) x_0 \end{equation}\]

이 공식을 사용하면 diffusion model $f_\theta$가 표준 언어 모델처럼 vocabulary 토큰에 대한 $\vert V \vert$개의 logit을 예측하는 동시에 $x_t$가 제공하는 다음 시퀀스 토큰에 대한 부분적인 정보를 활용할 수 있다. 이러한 단순성에도 불구하고, continuous한 출력을 사용하는 기존 diffusion model과 유사하게 inference 과정에서 연속적인 궤적을 그릴 수 있다.

2. L2D Inference Formulation

기존의 continuous diffusion model을 사용하여 새로운 샘플을 생성하는 효과적인 방법은 $f_\theta (x_t, t)$의 예측값 $\hat{x}$를 사용하여 각 timestep $t$에서 marginal distribution $p_t$를 보존하는 ODE를 구성하는 것이다. 하나의 diffusion process에 대해 이러한 유효한 ODE가 많이 존재하지만, 본 논문에서는 Rectified Flow의 공식을 채택하였다. 이 공식은 각 timestep $t$에서 denoising 궤적을 따라 일정한 속도 기대값을 산출하도록 설계되었다.

\[\begin{equation} dx_t = \frac{\hat{x} - x_t}{1 - t} \end{equation}\]

그런 다음 denoising process는 $t = 0$에서 시작하여, 순수한 noise로부터 $x_t$를 샘플링한 후, 이전 예측값들을 재사용하면서 $x_t$를 더 낮은 noise level $t + \Delta t$으로 이동시키는 방향인 $dx_t$를 따라 점진적으로 수행된다. 가장 간단한 경우 이 과정은 오일러 적분과 같으며, 다양한 요구 사항에 따라 모든 ODE solver를 사용할 수 있다.

Vocabulary에 대한 범주형 확률을 출력하는 이 예측은 continuous diffusion처럼 $dx_t$를 얻는 데 직접 사용될 수 없다. 그러나 이러한 확률을 $V$에 저장된 vocabulary 임베딩과 함께 사용하여 임의의 유효한 속도 $dx_t$에 대한 $\hat{x}$를 추정할 수 있다. CDCD는 $\hat{x}$를 임베딩에 대한 가중 평균으로 사용하는 반면, 본 논문에서는 $f_\theta$로 예측된 ​​확률을 사용하여 각 diffusion step $t$에서 개별 $\hat{x} \in V$를 샘플링한다. 이 두 추정값의 기대값은 일치하지만, 본 논문의 선택은 ODE가 추적하는 denoising 궤적에 약간의 확률성을 다시 도입한다. 실제로, 이러한 확률론적 특성은 diffusion 프레임워크의 자기 교정 특성 중 일부를 더 잘 활용하는 데 유용하다.

3. LMs as Single-step Diffusion Models

저자들이 L2D 디자인에서 내린 선택은 기존 LM 프레임워크와 명확한 연관성을 갖는다. $L^\textrm{CE}(\theta)$를 사용하여 diffusion model을 학습시키는 것은 표준적인 next-token prediction으로 해석될 수 있다. 여기서 모델에는 타겟 $y$에 대한 어느 정도의 지식이 포함된 추가 diffusion 토큰 $x_t$가 제공되며, 정보는 전혀 없음($t = 0$)에서 완전한 정보($t = 1$)까지 다양하다. 따라서 LM은 $t = 0$일 때 L2D와 동일한 loss로 본질적으로 학습되며, 여기서 $x_t$는 타겟 $y$와 전혀 상관관계가 없다. 마찬가지로, inference 시에는 모델의 logit에서 샘플링 예산 $T$까지 점점 더 정확한 다음 토큰 $\hat{x}$를 반복적으로 샘플링한다. 따라서 기존 LM 추론은 $T = 1$인 이 절차의 특수한 경우로 볼 수 있으며, 여기서는 모델의 첫 번째 샘플만 $y$를 예측하는 데 사용된다.

이러한 디자인 선택의 목적은 L2D가 새로운 모델을 처음부터 학습하는 것이 아니라, fine-tuning 방식을 통해 사전 학습된 LM을 확장하는 것을 목표로 한다는 것이다. 처음부터 diffusion 학습을 완전히 도입하는 것이 더 일반적일 수 있지만, 이는 기존 autoregressive 모델링에 내재된 학습 scalability와 강력한 inductive bias를 일부 상실할 위험이 있다. 또한, L2D는 기존 foundation model에 이미 인코딩된 광범위한 “system 1” 이해를 직접적으로 활용할 수 있도록 하며, 기존 능력을 기반으로 구축함으로써 엄청난 비용을 피할 수 있다.

L2D Implementation

저자들은 사전 학습된 transformer가 diffusion의 multi-step scaling 기능을 효율적으로 활용하면서도 원래의 single-step 생성 성능을 유지할 수 있도록 L2D 구현을 모듈식 확장으로 설계했다. 이를 위해 L2D는 아키텍처에 병렬적인 diffusion 경로를 도입했다. 이 경로에서는 diffusion 토큰 $x_t$가 전파되어 최종 layer의 고정된 메인 LM 경로에만 영향을 미친다.

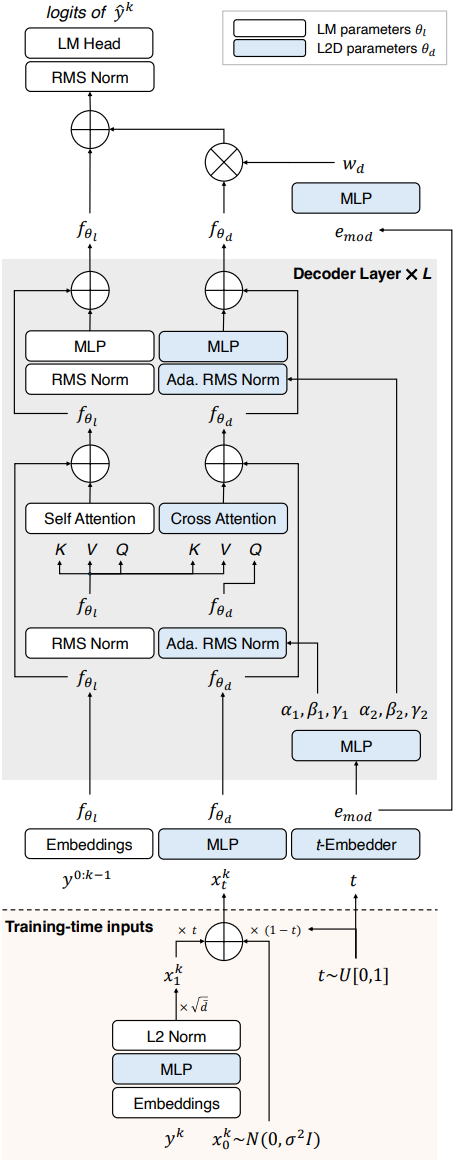
1. Diffusion Path Parametrization

구조 및 초기화

LM의 원래 아키텍처에 대한 별도의 병렬 경로 내에서 diffusion 토큰 $x_t$를 처리한다. 이 선택을 통해 컨텍스트 $c$에서 손상되지 않은 토큰을 처리하는 원래 능력을 잃을 위험 없이 모델 파라미터의 부분 집합만 최적화할 수 있다.

Transformer 아키텍처와 메인 경로 \(f_{\theta_l}\)과 동일한 수의 block을 사용하여 diffusion 경로 \(f_{\theta_d}\)를 구현한다. 각 block은 MLP block과 self-attention의 query layer에서 가져온 layer의 부분 집합으로 구성된다. 또한 사전 학습된 LM의 지식을 최대한 활용하기 위해, diffusion 경로의 모든 layer도 \(\theta_l\)의 가중치로 초기화한다.

실제로 이 초기화를 통해 간단한 LoRA로 diffusion 경로를 최적화할 수 있다. 또한, \(\theta_d\)와 \(\theta_l\) 모두에서 LM의 원래 가중치를 재사용하여 작은 LoRA 모듈만 저장하면 되므로 L2D의 메모리 오버헤드를 크게 최소화한다.

Diffusion 경로 구성 요소

Diffusion 경로의 transformer block은 일련의 residual MLP 모듈과 cross-attention 모듈로 구성된다. MLP 모듈은 \(f_{\theta_l}\)의 해당 모듈과 동일한 구조를 따르는 반면, cross-attention 모듈은 query와 output linear layer만 parameterize한다. 특히 cross-attention 동안 타겟 토큰 $y^k$에 대한 diffusion 토큰 $x_t^k$는 \(f_{\theta_l}\)의 해당 self-attention 모듈에서 이미 계산된 모든 이전 key와 value에 대해 attention을 수행한다. LM의 linear head 바로 앞, 모든 block 이후에 $f_\theta$에서 처리된 정보만 메인 경로로 다시 통합한다. 구체적으로, 두 경로를 \(f_{\theta_l} + w_d f_{\theta_d}\)로 병합하며, 여기서 diffusion 토큰 $x_t^k$의 rescale된 latent는 이전 토큰 $x^{k−1}$의 latent에 더해진다.

속성 및 장점

본 디자인 선택은 여러 토큰을 한 번에 생성하는 기존 diffusion 아키텍처에 비해 몇 가지 주요 장점을 가지고 있다. Inference 과정에서 \(f_{\theta_l}\)의 latent 표현을 KV 캐시와 함께 저장함으로써, diffusion step 수에 관계없이 생성된 각 토큰에 대해 메인 경로의 출력을 한 번만 계산하면 된다.

또한, $k$번째 타겟 토큰에 대한 diffusion 토큰은 이전 위치의 메인 경로에만 영향을 미치므로, 시퀀스 batch 차원에 걸쳐 학습을 완전히 병렬화하여 timestep $t_1, \ldots, t_k$의 샘플링과 diffusion 토큰 \(x_{t_1}^1, \ldots, x_{t_K}^K\)의 샘플링을 독립적으로 수행할 수 있다. 이를 통해 diffusion loss의 분산을 크게 완화하고, 데이터 batch에서 샘플링된 각 입력 컨텍스트 $x_0, \ldots, x_{K-1}$의 모든 $K$개의 시퀀스 위치에 대해 독립적인 diffusion loss를 효율적으로 얻을 수 있다.

2. L2D Conditioning

Diffusion space vocabulary

\(f_{\theta_d}\)를 컨디셔닝하기 위해, 기본 LM의 사전 학습된 토큰 vocabulary $V^l$로부터 diffusion 경로에 대한 discrete한 토큰 임베딩 집합을 포함하는 vocabulary $x \in V$를 구성한다. 특히, linear mapping $W_v \in \mathbb{R}^{\bar{d} \times d}$를 학습시켜 각 사전 학습된 임베딩 $V_y^l$을 $\bar{d}$차원의 저차원 임베딩으로 변환하고, 나중에 고정된 norm \(\sqrt{\bar{d}}\)로 rescaling한다.

\[\begin{equation} V_y = \sqrt{\bar{d}} \frac{W_v V_y^l}{\| W_v V_y^l \|_2}, \quad \forall y = 1, \ldots, \vert V \vert \end{equation}\]

이 정규화 단계는 학습하는 동안 샘플링된 노이즈 $x_0 \sim N(0, \sigma^2 I)$로 인한 손상 효과를 최소화하기 위해 $V$의 토큰 크기가 무한대로 증가하는 것을 방지한다. 이 방법은 $V$의 토큰 임베딩을 자연스럽게 분산시켜 데이터 매니폴드 전체에서 각 구성 요소마다 단위 분산을 갖는 분포를 생성한다. 마지막으로, diffusion 경로 시작 부분에 작은 2-layer MLP를 사용하여 diffusion 토큰 임베딩을 $d$차원으로 다시 매핑한다.

Timestep 컨디셔닝

현재 timestep $t \in [0, 1]$에 대하여 diffusion 경로를 세 가지 다른 방식으로 컨디셔닝한다.

1. 일반적인 diffusion model과 마찬가지로 $t$에서 sinusoidal feature를 추출하고 이를 작은 네트워크로 처리하여 \(f_{\theta_d}\)의 모든 layer normalization에 대한 shift 파라미터와 scale 파라미터를 얻는다.
2. 각 transformer block의 residual을 합산하기 전에 적용하는 추가적인 time-conditioned element-wise rescaling을 사용한다.
3. Diffusion 경로 \(f_{\theta_d}\)의 출력을 scaling하는 데 사용되는 가중치 항 $w_d$를 컨디셔닝하기 위해 timestep 임베딩을 사용한다.

그러나 처음 두 경우처럼 $w_d$를 네트워크 \(w_{\theta_d} (t)\)의 출력으로 만드는 대신, $w_d$를 \(w_{\theta_d} (0)\)의 값으로 shift한다.

\[\begin{equation} w_d (t) = w_{\theta_d} (t) - w_{\theta_d} (0) \end{equation}\]

이렇게 하면 $t = 0$에서 diffusion 경로가 항상 0으로 곱해져 \(f_{\theta_l}\)의 원래 출력이 변경되지 않는다. 따라서 $x_t$가 순수한 noise일 때 L2D가 사전 학습된 LM의 강력한 single-step 성능을 저하시키지 않도록 보장하며, $t$가 1로 증가하고 $x_t$가 더 많은 과거 계산 및 지식을 포함함에 따라 diffusion 경로가 예측에 점점 더 큰 영향을 미치도록 하는 강력한 inductive bias를 제공한다.

Classifier-free guidance

Classifier-free guidance를 통해 task 또는 데이터셋에 대한 추가적인 컨텍스트 정보를 기반으로 L2D 모델을 효과적으로 컨디셔닝할 수 있다. 학습 과정에서는 timestep 임베딩에 $J + 1$개의 옵션 집합 $g_0, \ldots, g_J$에서 학습된 클래스 임베딩을 더한다. 여기서 옵션 $g_0$는 추가적인 컨텍스트 정보가 제공되지 않을 때 적용되는 null 클래스 임베딩으로 사용되며, 주어진 dropout 확률로 학습된다. Inference 과정에서 task 레이블 $j \in (1, \ldots, J)$에 접근할 수 있다면, 가이드된 타겟 예측 \(\hat{x}_g\)를 구성할 수 있다.

\[\begin{equation} \hat{x}_g = w_g \times f_\theta (x_t, t, g_j, c) - (1 - w_g) \times f_\theta (x_t, t, g_0, c) \end{equation}\]

($w_g \ge 1$는 guidance 강도 파라미터)

이 방법은 diffusion model에 목표에 맞는 생성 능력을 효과적으로 제공하며, 사용자가 범용성과 특정 task 전문성을 절충할 수 있도록 한다.

Experimental Results

• 구현 디테일
  • $\sigma = 64$
  • $\bar{d} = 256$
  • optimizer: AdamW (100 warmup step + linear decay)

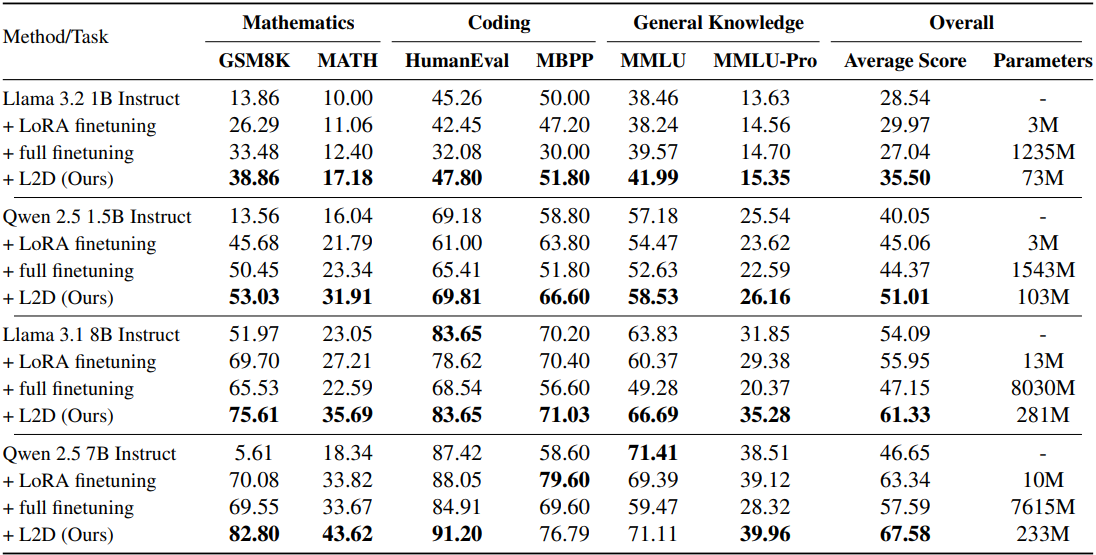
1. L2D Across Modern Large Language Models

다음은 다양한 언어 모델과의 성능 비교 결과이다.

2. Analysis and Extensions

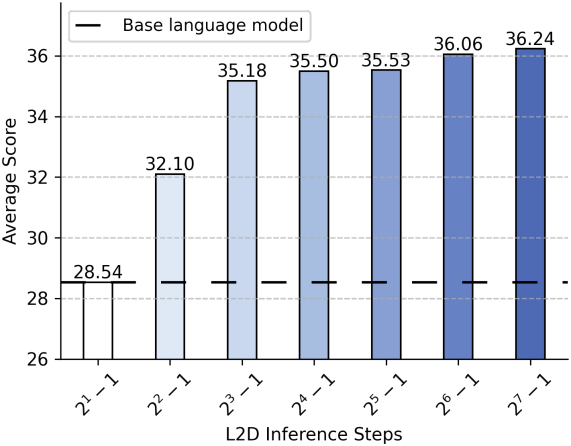
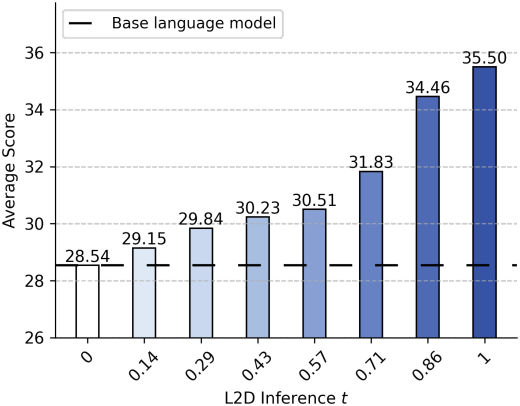
다음은 inference 시에 timestep $t$에 따른 L2D의 성능을 비교한 결과이다.

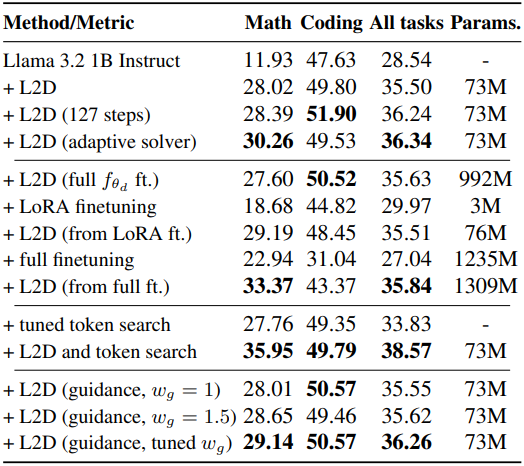
다음은 다양한 설정에 대한 L2D의 성능을 비교한 결과이다.

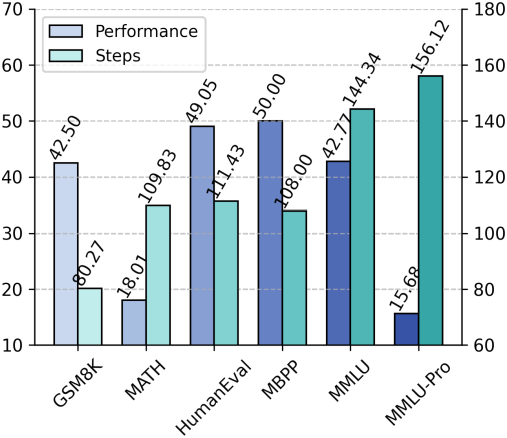
다음은 adaptive ODE solver를 사용하였을 때, task에 따른 성능과 step 수를 비교한 결과이다.

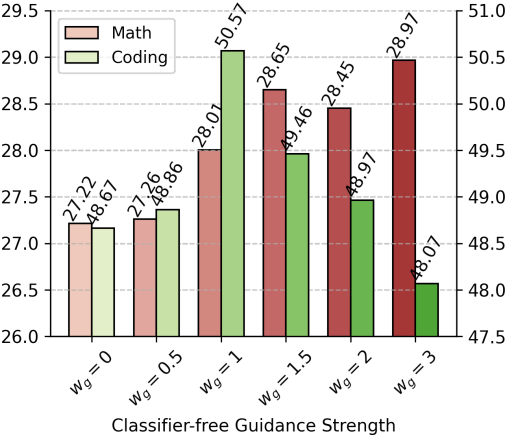
다음은 guidance 강도 $w_g$에 대한 효과를 비교한 결과이다.