[논문리뷰] K-Planes: Explicit Radiance Fields in Space, Time, and Appearance
CVPR 2023. [Paper] [Page] [Github]
Sara Fridovich-Keil, Giacomo Meanti, Frederik Warburg, Benjamin Recht, Angjoo Kanazawa
UC Berkeley | Istituto Italiano di Tecnologia | Technical University of Denmark
24 Jan 2023
Introduction
최근 동적인 radiance field에 대한 관심은 4D 볼륨에 대한 표현을 요구한다. 그러나 차원의 저주로 인해 4D 볼륨을 직접 저장하는 것은 엄청나게 비용이 많이 든다. 정적인 radiance field에 대한 3D 볼륨을 분해하기 위해 여러 가지 접근 방식이 제안되었지만, 이는 고차원 볼륨으로 쉽게 확장되지 않는다.
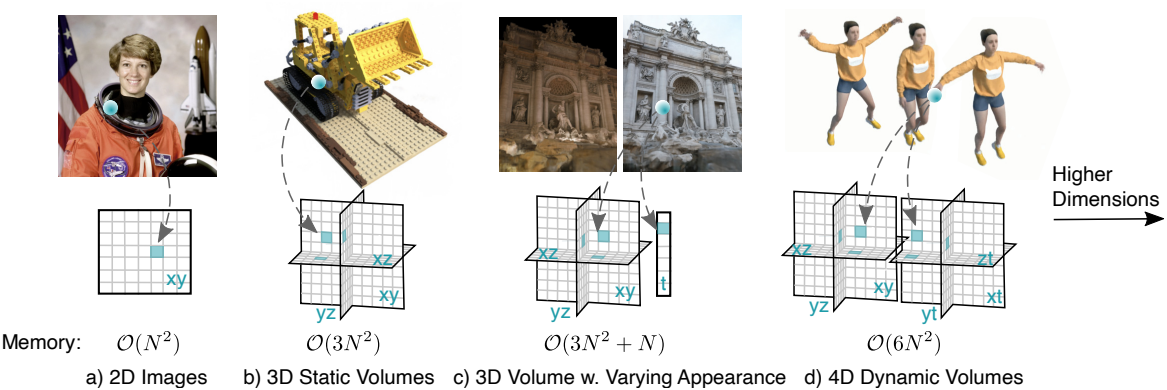
본 논문은 간단하고, 해석 가능하고, 컴팩트하며, 빠른 학습과 렌더링을 제공하는 4D 볼륨의 분해를 제안하였다. 구체적으로, 4D 볼륨을 표현하기 위해 6개의 평면을 사용하는데, 3개는 공간을 나타내고 나머지 3개는 시공간 변화를 나타낸다. 공간과 시공간을 이렇게 분해하면 모델을 해석할 수 있다. 즉, 동적 객체는 시공간 평면에서 명확하게 볼 수 있는 반면, 정적 객체는 공간 평면에서만 나타난다. 이러한 해석 가능성은 시간과 공간에서 차원별 prior를 가능하게 한다.
보다 일반적으로, 2D 평면으로 모든 차원의 분해를 선택한다. $d$차원 공간의 경우, $k = \binom{d}{2}$개 평면으로 구성된 k-planes를 사용하며, 이는 모든 차원 쌍을 나타낸다. 예를 들어, 4차원의 경우 hex-planes를 사용하고, 3차원의 경우 tri-planes를 사용한다. 다른 평면 세트를 선택하면 $k$개 이상의 평면을 사용하여 불필요한 메모리를 차지하거나 더 적은 평면을 사용하여 $d$차원 중 두 차원 간의 잠재적 상호 작용을 표현하는 능력을 포기하게 된다.
대부분의 radiance field는 MLP를 사용하면서 일부 블랙박스 요소를 수반한다. 그 대신, 저자들은 k-planes가 이전 블랙박스 모델과 비슷하거나 더 나은 재구성 품질을 유지하면서 화이트박스 모델이 될 수 있도록 하는 데 있어 두 가지 설계 선택이 근본적이라고 생각하였다.
- k-planes의 feature들은 더해지는 것이 아니라 서로 곱해진다.
- 선형 feature 디코더는 뷰에 따른 색상에 대한 학습된 basis를 사용하여 가변적인 모양의 장면을 모델링하고 더 큰 적응성을 가진다.
MLP 디코더는 평면이 곱해질 때만 이 선형 feature 디코더로 대체될 수 있으며, 이는 MLP 디코더가 뷰에 따른 색상과 공간 구조 결정에 모두 관여한다는 것을 시사한다.
4D 볼륨을 2D 평면으로 분해하면 MLP에 의존하지 않고도 높은 압축 수준을 얻을 수 있으며, 직접 표현하려면 300GB 이상이 필요한 4D 볼륨을 200MB를 사용하여 표현한다. 게다가 커스텀 CUDA 커널을 사용하지 않음에도 불구하고 k-planes는 이전의 implicit한 모델보다 10배 빠르게 학습된다.
K-planes model

본 논문은 임의의 차원에서 장면을 표현하기 위한 간단하고 해석 가능한 모델을 제안하였으며, 낮은 메모리 사용량과 빠른 학습 및 렌더링을 제공한다. K-planes factorization은 두 차원의 모든 조합을 표현하는 $k = \binom{d}{2}$개의 평면을 사용하여 $d$차원 장면을 모델링한다.
예를 들어, 3D 장면의 경우 xy, xz, yz를 표현하는 3개의 평면을 갖는 tri-planes가 된다. 4D 장면의 경우 xy, xz, yz, xt, yt, zt를 표현하는 6개의 평면을 갖는 hex-planes가 된다. 5D 공간을 표현하고자 하는 경우 10개의 평면을 사용한다.
1. Hex-planes
Hex-planes factorization은 6개의 평면을 사용한다. 공간 평면을 \(\textbf{P}_{xy}\), \(\textbf{P}_{xz}\), \(\textbf{P}_{yz}\)라고 하며, 시공간 평면을 \(\textbf{P}_{xt}\), \(\textbf{P}_{yt}\), \(\textbf{P}_{zt}\)라고 한다. 설명을 간단하게 하기 위해 대칭적인 공간 및 시간 해상도를 $N$이라 하면, 각 평면은 $N \times N \times M$ 형태를 가지며, 여기서 $M$은 장면의 밀도와 뷰에 따른 색상을 포착하는 feature의 크기이다.
4D 좌표 $\textbf{q} = (i, j, k, \tau)$에서의 feature의 entry들을 $[0, N)$ 사이로 정규화하고 이를 6개의 평면에 projection한다.
\[\begin{equation} f(\textbf{q})_c = \psi (\textbf{P}_c, \pi_c (\textbf{q})) \end{equation}\]여기서 $\pi_c$는 $\textbf{q}$를 평면 $c \in C$에 projection하고 $\psi$는 규칙적으로 간격이 있는 2D 그리드에서의 bilinear interpolation을 나타낸다. 각 평면 $c$에 대해 위 식을 반복하여 feature \(f(\textbf{q})_c\)를 얻고, Hadamard product (element-wise multiplication)을 사용하여 6개 평면의 feature를 결합하여 길이가 $M$인 최종 feature 벡터를 생성한다.
\[\begin{equation} f(\textbf{q}) = \prod_{c \in C} f(\textbf{q})_c \end{equation}\]이러한 feature들은 선형 디코더나 MLP를 사용하여 색상과 밀도로 디코딩된다.
왜 Hadamard product인가?
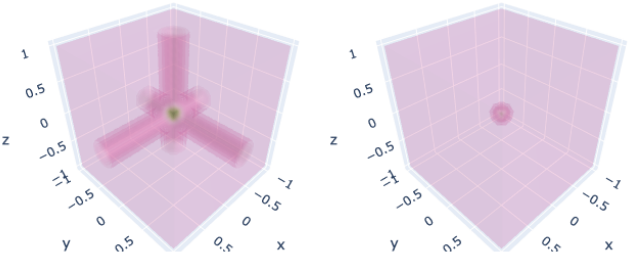
(왼쪽은 plane feature들을 element-wise로 더함, 오른쪽은 element-wise로 곱함)
3D에서 k-planes는 tri-planes factorization으로 축소되는데, 이는 element가 곱해진다는 점을 제외하면 기존 tri-plane 모델과 유사하다. 자연스러운 질문은 왜 이전 연구들에서 사용했던 것처럼 더하지 않고 곱하는가이다. 위 그림에서 볼 수 있듯이 곱셈으로 평면을 결합하면 k-planes가 공간적으로 제한된 신호를 생성할 수 있음을 보여주는데, 이는 덧셈에서는 불가능하다.
Hadamard product의 이러한 선택 능력은 선형 디코더에 대한 상당한 렌더링 개선과 MLP 디코더에 대한 적당한 개선을 제공한다. 이는 MLP 디코더가 뷰에 따른 색상과 공간 구조 결정에 모두 관여한다는 것을 시사한다. Hadamard product는 feature 디코더의 이러한 추가 작업을 덜어주고 뷰에 따른 색상만을 담당하는 선형 디코더를 사용하여 유사한 성능을 달성할 수 있게 한다.
2. Interpretability
공간-공간 평면과 공간-시간 평면을 분리하면 모델을 해석할 수 있고 차원별 prior를 통합할 수 있다. 예를 들어, 장면이 전혀 움직이지 않으면 시간 성분은 항상 1이 되므로 공간 평면의 feature만 사용하고, 정적 영역을 쉽게 식별하고 컴팩트하게 표현할 수 있으므로 압축 이점이 있다. 또한 공간-시간 분리는 해석 가능성을 개선한다. 즉, 시간-공간 평면에서 1이 아닌 요소를 시각화하여 시간의 변화를 추적할 수 있다. 이러한 단순성, 분리 및 해석 가능성 덕분에 prior를 간단하게 추가할 수 있다.
멀티스케일 평면
공간적 부드러움과 일관성을 장려하기 위해, 모델은 64, 128, 256, 512와 같이 서로 다른 공간 해상도에서 여러 사본을 가지고 있다. 각 스케일의 모델은 개별적으로 처리되고, 다른 스케일의 $M$차원 feature 벡터는 디코더로 전달되기 전에 함께 concatenate된다. 이 표현은 서로 다른 스케일에서 feature를 효율적으로 인코딩하여 가장 높은 해상도에서 저장된 feature 수를 줄이고 그로 인해 모델을 더욱 압축할 수 있다. 또한, 저자들은 시간 차원을 여러 스케일에서 표현할 필요가 없다는 것을 발견했다.
공간에서의 Total Variation
공간적 total variation의 정규화는 L1 norm 또는 L2 norm을 장려한다. 각 공간-시간 평면은 공간 차원에 대한 1D에서, 공간-공간 평면은 2D에서 정규화한다.
\[\begin{equation} \mathcal{L}_\textrm{TV} (\textbf{P}) = \frac{1}{\vert C \vert n^2} \sum_{c,i,j} ( \| \textbf{P}_c^{i,j} - \textbf{P}_c^{i-1,j} \|_2^2 + \| \textbf{P}_c^{i,j} - \textbf{P}_c^{i,j-1} \|_2^2 ) \end{equation}\]저자들은 L2 norm을 사용했지만 L2나 L1이나 비슷한 품질을 생성한다.
시간에서의 Smoothness
1D Laplacian (2차 미분) 필터를 사용하여 부드러운 모션을 촉진한다.
\[\begin{equation} \mathcal{L}_\textrm{smooth} (\textbf{P}) = \frac{1}{\vert C \vert n^2} \sum_{c,i,t} \| \textbf{P}_c^{i,t-1} - 2 \textbf{P}_c^{i,t} + \textbf{P}_c^{i,t+1} \|_2^2 \end{equation}\]급격한 가속은 페널티를 부과한다. 이 정규화는 공간-시간 평면의 시간 차원에만 적용한다.
Sparse transients
장면의 정적 부분을 공간-공간 평면으로 모델링하는 것이 목표이다. 공간-시간 평면의 feature를 1로 초기화하고 학습 중에 이 평면에 $\ell_1$ regularizer를 사용하여 공간과 시간을 분리하도록 권장한다.
\[\begin{equation} \mathcal{L}_\textrm{sep} (\textbf{P}) = \sum_{c \in \{xt, yt, zt\}} \| \textbf{1} - \textbf{P}_c \|_1 \end{equation}\]이를 통해 공간-시간 평면의 feature는 해당 공간의 내용이 시간에 따라 변하지 않는다면 1로 고정된다.
3. Feature decoders
저자들은 feature 벡터 $f(\textbf{q})$를 밀도 $\sigma$와 뷰에 다른 색상 $\textbf{c}$로 디코딩하는 두 가지 방법을 제안하였다.
학습된 color basis: 선형 디코더와 명시적 모델
Plenoxels, Plenoctrees, TensoRF에서는 feature가 spherical harmonic (SH) 계수로 사용되어 색상을 모델링하였다. 이러한 SH 디코더는 MLP 디코더에 비해 고충실도 재구성과 향상된 해석성을 제공할 수 있다. 그러나 SH 계수는 최적화하기 어렵고, 표현력은 사용된 SH 기반 함수의 수에 의해 제한되며, 종종 제한된 표현으로 흐릿한 반사가 발생한다.
그 대신, SH 함수를 학습된 basis로 대체하여 선형 디코더의 계수로 feature를 처리하는 해석성을 유지하면서도 basis의 표현력을 높이고 각 장면에 적응할 수 있도록 한다. 각 뷰 방향 $\textbf{d}$를 각각 RGB basis 벡터 \(b_R (\textbf{d}), b_G (\textbf{d}), b_B (\textbf{d}) \in \mathbb{R}^M\)에 매핑하는 작은 MLP를 사용하여 basis를 표현한다. MLP는 SH basis 함수를 대체하며, 다음과 같이 색상 값을 얻는다.
\[\begin{equation} \textbf{c} (\textbf{q}, \textbf{d}) = \bigcup_{i \in \{R,G,B\}} f(\textbf{q}) \cdot b_i (\textbf{d}) \end{equation}\]($\cdot$는 내적, $\cup$는 concatenation)
마찬가지로 뷰 방향과 무관하게 학습된 basis $b_\sigma \in \mathbb{R}^M$을 사용하여 밀도에 대한 선형 디코더로 사용한다.
\[\begin{equation} \sigma (\textbf{q}) = f (\textbf{q}) \cdot b_\sigma \end{equation}\]최종적으로 $\textbf{c}$에 sigmoid를 적용하고 $\sigma$에 exponential을 적용하여 유효 범위에 포함되도록 강제한다.
MLP 디코더: 하이브리드 모델
본 논문의 모델은 Instant-NGP나 DVGO와 같이 MLP 디코더와 함께 사용할 수 있다. 이 버전에서 feature는 두 개의 작은 MLP, $g_\sigma$와 $g_\textrm{RGB}$에 의해 디코딩된다.
\[\begin{aligned} \sigma (\textbf{q}), \hat{f} (\textbf{q}) &= g_\sigma (f (\textbf{q})) \\ \textbf{c} (\textbf{q}, \textbf{d}) &= g_\textrm{RGB} (\hat{f} (\textbf{q}), \gamma (\textbf{d})) \end{aligned}\]선형 디코더의 경우와 마찬가지로 예측된 밀도 및 색상 값은 각각 exponential과 sigmoid를 통해 최종적으로 정규화된다.
4. Optimization details
Contraction and normalized device coordinates
앞을 향한 장면의 경우, 무제한 깊이를 가능하게 하면서 해상도를 더 잘 할당하기 위해 normalized device coordinates (NDC)를 적용한다. 또한 Mip-NeRF 360에서 제안된 contraction의 $\ell_\infty$ 버전 ($\ell_2$가 아님)을 구현하여 Phototourism 장면에 사용한다.
Proposal sampling
Mip-NeRF 360의 proposal sampling 전략을 사용하며, 밀도 모델로 k-planes의 작은 인스턴스를 사용한다. Proposal sampling은 광선을 따라 밀도 추정치를 반복적으로 정제하여 더 높은 밀도 영역에 더 많은 포인트를 할당한다. 2단계 샘플러를 사용하여 전체 모델에서 평가해야 하는 샘플이 줄어들고 해당 샘플을 물체 표면에 더 가깝게 배치하여 더 선명한 디테일을 얻을 수 있다. Proposal sampling에 사용되는 밀도 모델은 histogram loss로 학습된다.
Importance sampling
멀티뷰 동적 장면의 경우, DyNeRF의 시간 차이에 기반한 중요도 샘플링 (IST) 전략을 사용한다. 최적화의 마지막 부분에서, 25프레임 전후의 색상 변화에 비례하여 학습 광선을 샘플링한다. 이는 동적 영역에서 더 높은 샘플링 확률을 가져온다. 정적 장면이 균일하게 샘플링된 광선으로 수렴한 후에 이 전략을 적용한다. IST는 전체 프레임 메트릭에 미치는 영향이 미미하지만 작은 동적 영역에서 시각적 품질을 개선한다. 중요도 샘플링은 단안 동영상이나 카메라가 움직이는 데이터셋에는 사용할 수 없다.
Results
1. Static scenes
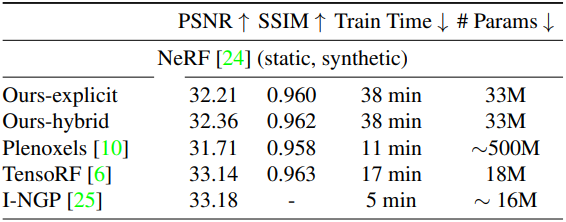
다음은 NeRF 장면에서의 결과이다.

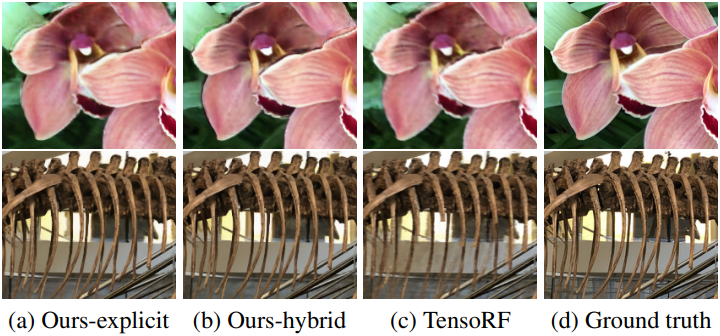
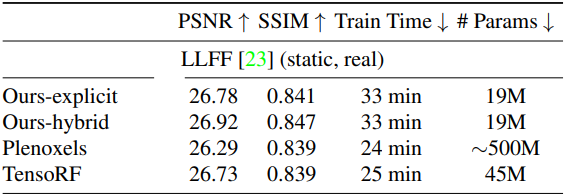
다음은 LLFF 장면에서의 결과이다.
2. Dynamic scenes
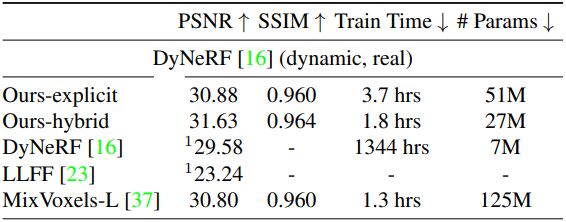
다음은 DyNeRF 장면에서의 결과이다.

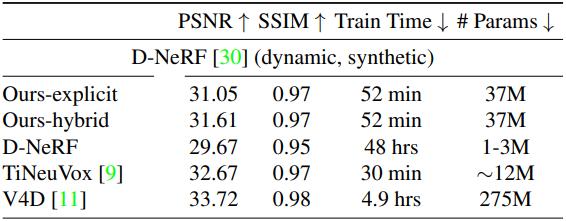
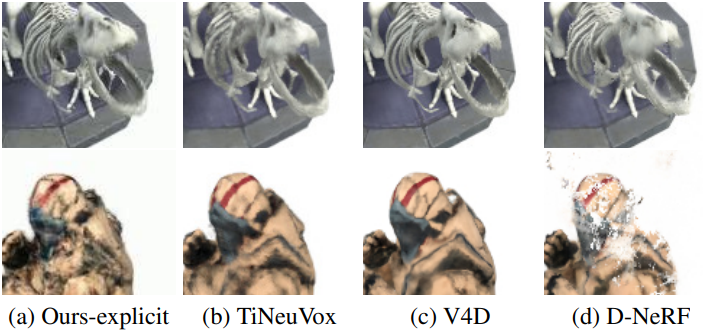
다음은 D-NeRF 장면에서의 결과이다.
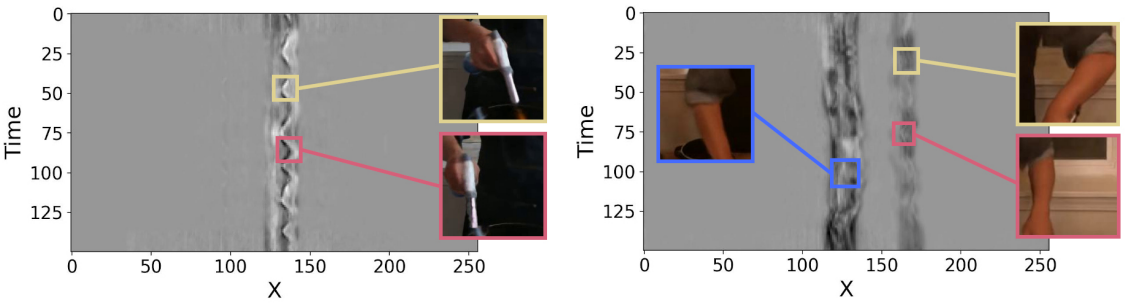
다음은 공간과 시간으로 분리한 예시이다.

다음은 시간 평면을 시각화한 것이다.
3. Variable appearance
다음은 Phototourism 장면에서의 결과이다.