[논문리뷰] Adding Additional Control to One-Step Diffusion with Joint Distribution Matching
ICCV 2025. [Paper]
Yihong Luo, Tianyang Hu, Yifan Song, Jiacheng Sun, Zhenguo Li, Jing Tang
HKUST | Huawei Noah’s Ark Lab | HKUST (GZ)
9 Mar 2025

Introduction
현재 1-step student 모델에 대한 추가 제어 학습은 연구가 부족한 상태이다. 기본 diffusion model에 대한 추가 제어 학습은 일반적으로 denoising score matching을 통해 최적화된 사전 학습된 ControlNet 모델에 의존한다. 그러나 1-step 생성을 위해 ControlNet을 확장하면 심각한 한계가 발생하여 1-step generator에 제어 메커니즘을 더 잘 통합하는 새로운 학습 패러다임의 필요하다.
한편, diffusion distillation 과정에서 추가 제어를 통합하는 것 또한 어렵다. 1-step 생성을 위한 현재의 diffusion distillation 방법론은 teacher 모델의 기능을 복제하는 student 모델을 distillation하는 데 주로 초점을 맞추고 있으며, teacher의 능력을 넘어서는 student의 능력을 확장하는 방법이 연구되지 않았다. 이러한 한계는 특히 원래 diffusion model이 처리하도록 설계되지 않은 새로운 제어를 추가할 때 중요하다.
이러한 과제를 해결하기 위해, 본 논문에서는 이미지-조건 결합 분포 간의 reverse KL divergence를 최소화하는 JDM이라는 새로운 접근법을 제안하였다. 저자들은 reverse KL divergence에 대한 다루기 쉬운 상한(upper bound)을 도출하여 충실도 학습과 조건 학습을 효과적으로 분리하였다. 본 논문의 비대칭적 목적 함수는 teacher 모델은 모르는 제어를 처리할 수 있는 1-step student 모델을 얻을 수 있도록 한다.
또한, 이러한 분리 메커니즘은 classifier-free guidance (CFG)의 활용도를 향상시킬 뿐만 아니라, 인간 피드백 학습(HFL)을 학습 과정에 원활하게 통합할 수 있도록 한다. 결과적으로, JDM은 생성된 이미지의 제어 가능성과 품질을 모두 향상시켜 1-step diffusion 생성을 위한 더욱 유연하고 효율적인 프레임워크를 제공한다.
JDM은 제어 가능한 multi-step diffusion model보다 더 나은 성능을 달성하였으며 (14.58 vs 15.21), 1-step 모델 중 SOTA 성능을 확립하였다. 특히, 더 나은 CFG를 적용한 본 논문의 모델은 33.97점의 CLIP 점수를 달성하여 multi-step diffusion model의 33.03점을 크게 앞질렀다.
Method
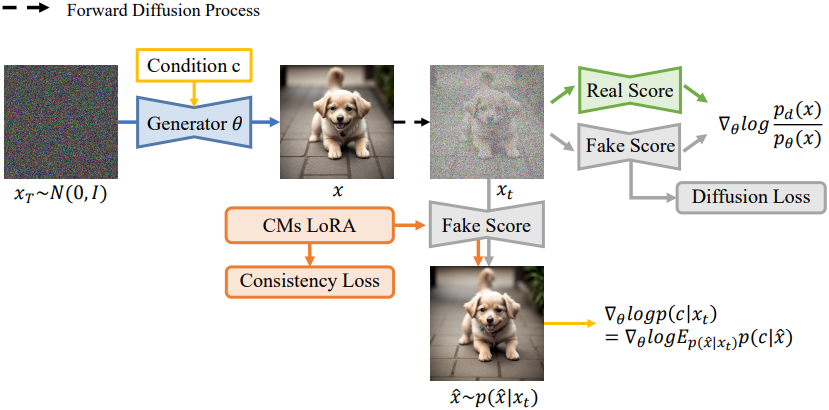
Problem Setup
Multi-level score network \(s_\phi (\textbf{x}_t, t)\)를 갖는 사전 학습된 diffusion model을 고려하자.
\[\begin{equation} s_\phi (\textbf{x}_t, t) = \nabla_{\textbf{x}_t} \log p_\phi (\textbf{x}_t, t) \approx \nabla_{\textbf{x}_t} \log p_t (\textbf{x}_t) \end{equation}\]이 사전 학습된 모델은 데이터 분포 $p_d$에 대한 고품질 근사를 제공하며, \(p(\textbf{x}_0) \approx p_d\)를 만족한다고 가정한다. 또한, 조건부 discriminative model $\log p(c \vert \textbf{x})$로 주어진 새로운 제어 $c$를 구현하고자 한다.
본 논문의 목표는 추가 제어 $c$를 포함하는 1-step generator를 학습하는 것이다. 본 논문의 목표는 student 모델이 teacher 모델보다 더 새로운 역량을 획득할 수 있도록 하는 알고리즘을 개발하는 것이다.
1-step student 학습에 새로운 제어를 직접 주입하기 위해, 저자들은 \(p_\theta (\textbf{x}_t, c)\)와 \(p(\textbf{x}_t, c)\) 사이의 joint reverse KL divergence를 최소화하는 것을 제안하였다.
\[\begin{aligned} &\mathbb{E}_t \lambda_t \textrm{KL} (p_\theta (\textbf{x}_t, c) \,\|\, p (\textbf{x}_t, c)) \\ &= \mathbb{E}_t \lambda_t \textrm{KL} (p_\theta (\textbf{x}_t \vert c) p(c) \,\|\, p(c \vert \textbf{x}_t) p_\phi (\textbf{x}_t)) \end{aligned}\]($p(c)$는 알려진 고정 분포)
특히, 이 joint KL divergence는 목표 분포와 student 분포 사이에 비대칭성을 보인다. 목표 분포는 \(p_\phi (\textbf{x})\)와 \(p(c \vert \textbf{x}_t)\)로 분해되며, student 분포는 discriminative model을 통해 접근 가능하다. 이 공식을 통해 teacher 모델이 모르는 조건을 처리하는 1-step 조건부 student 모델을 도출할 수 있다.
그러나 위 식에서 KL divergence를 최소화하려면 여전히 student의 gradient에 접근할 수 있어야 한다. 다행히도 다음과 같이 다루기 쉬운 상한(upper bound)에 접근할 수 있다.
\[\begin{aligned} &\mathbb{E}_t \lambda_t \textrm{KL} (p_\theta (\textbf{x}_t, c) \,\|\, p (\textbf{x}_t, c)) \\ &\le \lambda_t \mathbb{E}_{p_\theta (\textbf{x} \vert c) p(c), t} [- \log p (c \vert \textbf{x}_t) p_\phi (\textbf{x}_t) + \log p_\theta (\textbf{x}_t)] \end{aligned}\]\(p_\theta (\textbf{x} \vert c)\)의 학습을 위한 gradient의 상한은 다음과 같이 계산할 수 있다.
\[\begin{equation} \textrm{Grad} (\theta) = - \alpha_t \mathbb{E}_{p_\theta (\textbf{x} \vert c) p(c), t} \lambda_t [\underbrace{\nabla_{\textbf{x}_t} \log p(c \vert \textbf{x}_t)}_{\textrm{condition learning}} + \underbrace{\nabla_{\textbf{x}_t} \log \frac{p_\phi (\textbf{x}_t)}{p_\theta (\textbf{x}_t)}}_{\textrm{fidelity learning}}] \frac{\partial \textbf{x}}{\partial \theta} \end{equation}\]\(\nabla_{\textbf{x}_t} \log p_\theta (\textbf{x}_t)\)를 score model \(s_\psi (\textbf{x}_t, t)\)로 근사할 수 있으며, 이는 \(s_\phi (\textbf{x}_t, t)\)를 통한 초기화를 통해 쉽게 학습할 수 있다. $s_\phi$를 real score, $s_\psi$를 fake score라고 부른다.
이 상한값은 자연스럽게 조건부 정렬과 생성 충실도라는 두 가지 학습 요소로 분해된다. 이는 fake score가 두 학습 요소에 모두 관여하는 VSD나 diff-instruct와는 다르다. 본 논문의 접근법은 fake score에 대한 부담을 줄이는 동시에 teacher가 학습 조건을 이해해야 할 필요성을 제거하였다.
Fake score 학습
\(\nabla_{\textbf{x}_t} \log p_\theta (\textbf{x}_t)\)를 모델링하기 위해 보조 diffusion model $s_\psi$를 사용한다. Fake score는 denoising을 통해 효율적으로 학습될 수 있다.
\[\begin{equation} \mathbb{E}_{t, \epsilon, p_\theta (\textbf{x})} \| \epsilon_\psi (\textbf{x}_t, t) - \epsilon \| \\ \textrm{where} \quad \textbf{x}_t = \alpha_t \textbf{x} + \sigma_t \epsilon \end{equation}\]학습 후 다음과 같이 \(\nabla_{\textbf{x}_t} \log p_{\theta, t} (\textbf{x}_t)\)를 구할 수 있다.
\[\begin{equation} \nabla_{\textbf{x}_t} \log p_{\theta, t} (\textbf{x}_t) \approx s_\psi (\textbf{x}_t, t) = − \frac{\epsilon_\psi (\textbf{x}_t, t)}{\sigma_t} \end{equation}\]\(\log p(c \vert \textbf{x}_t)\) 모델링
안타깝게도 조건부 정렬 밀도는 대부분의 경우 깨끗한 샘플을 기준으로 정의되며, noise가 추가된 샘플을 기준으로 정의되는 경우는 드물다. 따라서 이를 근사하는 방법을 찾아야 한다. \(\log p(c \vert \textbf{x}_t)\)는 다음과 같이 모델링할 수 있다.
\[\begin{aligned} p(c \vert \textbf{x}_t) &= \int p(c \vert \textbf{x}_t, \textbf{x}) p (\textbf{x} \vert \textbf{x}_t) d \textbf{x} \\ &= \int p(c \vert \textbf{x}) p (\textbf{x} \vert \textbf{x}_t) d \textbf{x} \end{aligned}\]조건 $c$는 $\textbf{x}$에 완전히 의존하므로 \(p(c \vert \textbf{x}_t, \textbf{x})\)를 \(p(c \vert \textbf{x})\)로 대체할 수 있다. 남은 과제는 \(p (\textbf{x} \vert \textbf{x}_t)\)를 모델링하는 방법이다.
저자들은 implicit generator를 사용하여 \(p (\textbf{x} \vert \textbf{x}_t)\)를 parameterize하는 것을 제안하였다. 쉬운 방법은 fake score를 사용하여 직접 parameterize하는 것이다. 그러나 분포는 깨끗한 샘플에 대해 정의되므로 fake score를 사용하면 분포를 정확하게 추정할 수 없다. 따라서 LoRA fine-tuning을 통해 fake score에 대해 효율적으로 학습할 수 있는 consistency model을 사용하여 parameterize한다.
\(p (\textbf{x} \vert \textbf{x}_t)\) 학습
\(p (\textbf{x} \vert \textbf{x}_t)\)는 consistency model로 모델링되며, 효율성을 위해 fake score에 LoRA를 삽입하여 모델을 학습시킨다. 구체적으로, consistency model은 다음을 통해 효율적으로 학습될 수 있다.
\[\begin{equation} \end{equation}\]1. Learning Better Aligned One-Step Generator
인간 피드백 통합
본 프레임워크에 인간 피드백 학습(HFL)을 완벽하게 통합될 수 있다. 구체적으로, “인간이 선호하는 이미지”를 하나의 컨디셔닝 요소로 도입한다. 단 하나의 조건만 다루므로, 원하는 generator에 해당 조건을 주입할 필요가 없다. 따라서 학습 gradient는 다음과 같다.
\[\begin{equation} \textrm{Grad}(\theta) = - \alpha_t \mathbb{E}_{p_\theta (\textbf{x}_t \vert c) p(c), t} \lambda_t [\nabla_{\textbf{x}_t} r (\textbf{x}_t) + \nabla_{\textbf{x}_t} \log \frac{p_\phi (\textbf{x}_t)}{p_\theta (\textbf{x}_t)}] \frac{\partial \textbf{x}}{\partial \theta} \\ \textrm{where} \quad \nabla_{\textbf{x}_t} r (\textbf{x}_t) = \nabla_{\textbf{x}_t} \log p (\textrm{"Human-preferred images"} \vert \textbf{x}_t) \end{equation}\]분리된 CFG
본 프레임워크는 조건 학습과 충실도 학습을 두 가지 뚜렷한 구성 요소로 구분한다. 조건부 확률 \(p(c \vert \textbf{x}_t)\)가 텍스트-이미지 정렬을 나타낼 때, 그 gradient는 classifier-free guidance (CFG)를 사용하여 계산할 수 있다. 기존 접근법들은 distillation 과정에서 CFG를 사용했지만, CFG는 real score와 결합되어 있다. 이와는 대조적으로, 본 프레임워크는 조건부 학습에 CFG를 명시적으로 활용한다. 이러한 주요 차이점 덕분에 real score 계산에 사용되는 것과는 다른 diffusion model을 사용하여 CFG를 계산할 수 있으며, 이를 통해 더욱 정교한 diffusion model을 사용하여 텍스트-이미지 정렬을 유도할 수 있다.
2. Learning One-Step Generator with Additional Control
제어 가능한 생성
ControlNet과 유사한 추가 제어 기능을 통합하기 위해, student 모델을 연관된 ControlNet을 갖는 diffusion model로 parameterize한다. Generator의 학습 objective는 다음과 같다.
\[\begin{equation} \min_{\theta, \beta} - \mathbb{E}_{p_{\theta, \beta} (\textbf{x}_t \vert c) p(c), t} \lambda_t [\log p (c \vert \textbf{x}_t) + \log \frac{p_{\phi, t} (\textbf{x}_t)}{p_{\psi, t} (\textbf{x}_t)}] \end{equation}\]($\beta$는 ControlNet의 추가 파라미터)
이 공식은 비대칭적 기능 개발을 가능하게 한다. 즉, student 모델은 teacher 모델의 능력을 넘어서는 조건부 생성 과제를 학습할 수 있다.
Shared One-Step Generator Between Different Additional Control
위 식은 1-step generator \(G_\theta\)와 ControlNet $\phi$의 공동 학습을 설정하지만, 이 접근법은 새로운 제어 조건마다 \(G_\theta\) 전체를 재학습해야 한다. 이러한 요구 사항은 계산 리소스와 저장 공간의 비효율적인 사용을 초래하여 실제 적용에 제약을 준다.
간단한 해결책은 diff-instruct를 사용하여 제어 없이 \(G_\theta\)를 먼저 학습시킨 다음, ControlNet을 학습시켜 \(G_\theta\)에 추가 제어를 통합하는 것이다. 그러나 이러한 방식으로 학습된 \(G_\theta\)는 mode collapse 현상을 겪어 추가 제어 신호를 수용하기 어렵다. DMD와 같이 teacher 모델을 사용하여 수백만 개의 noise-이미지 쌍을 생성한 다음, \(G_\theta\)에 ODE regression loss를 추가할 수도 있지만, 이 방법은 계산적으로 매우 비효율적이다.
이러한 한계점을 해결하기 위해, 본 논문에서는 새로운 2단계 warm-up 학습 전략을 제안하였다.
- 초기 단계: 주요 조건에 대해 \(G_\theta\)와 ControlNet의 공동 학습
- 확장 단계: 후속 조건에 대해 ControlNet만 학습하면서 \(G_\theta\)를 고정
이 접근법은 joint KL divergence를 활용하여 초기 학습 과정에서 \(G_\theta\)를 정규화하여 조건에 더 잘 적응하고 mode collapse를 방지한다. 결과적으로 잘 학습된 \(G_\theta\)는 다른 형태의 제어를 효과적으로 통합할 수 있다.
Experiments
1. Controllable Generation
다음은 다양한 조건 신호에 대한 생성 결과를 비교한 것이다.


2. Other Application in Text-to-Image Generation
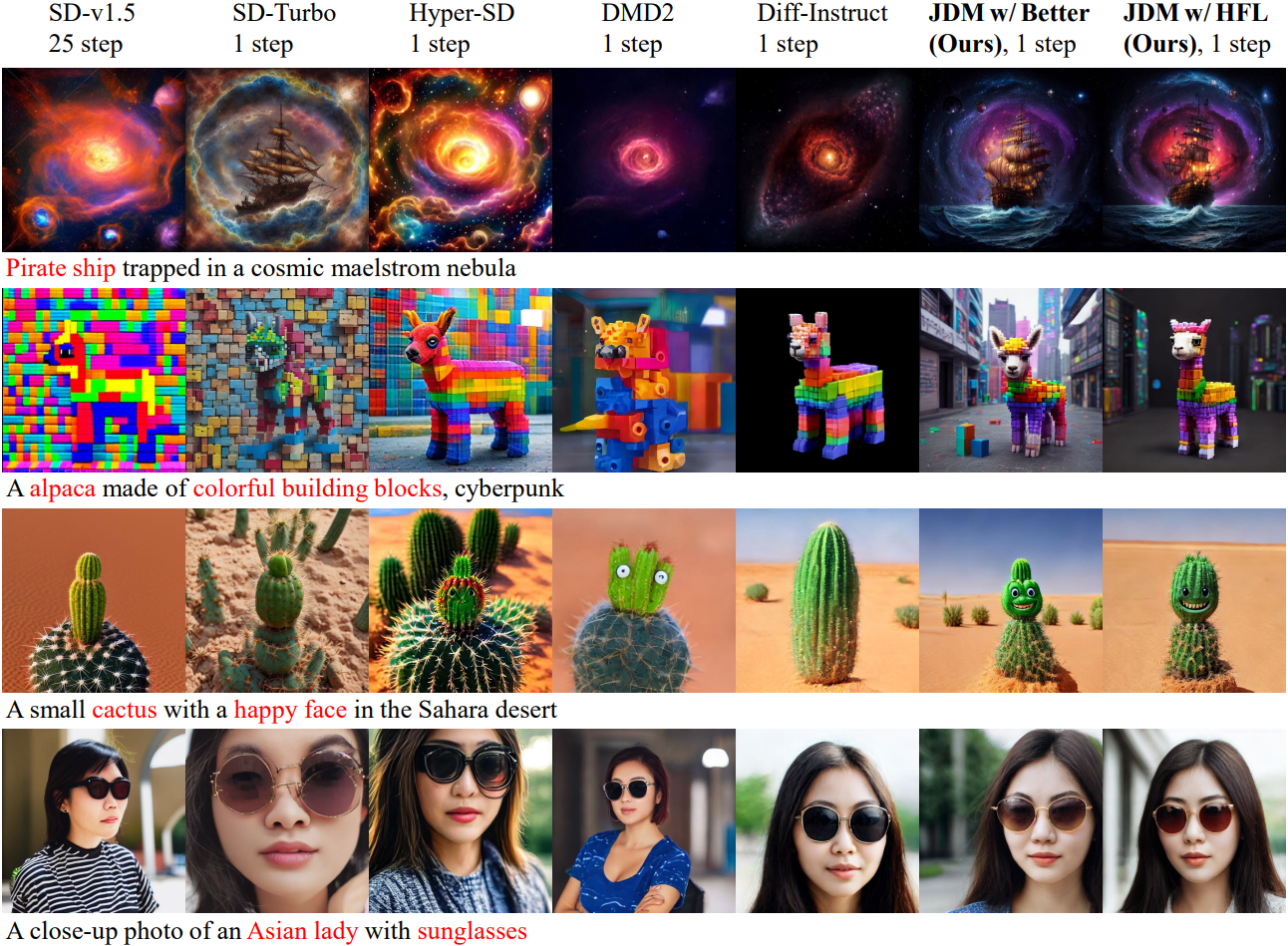
다음은 다양한 text-to-image 모델과 비교한 결과이다.

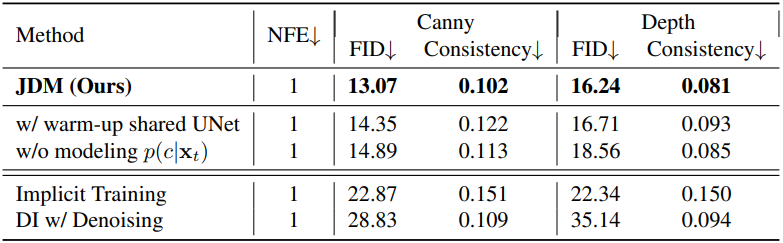
3. Ablation Study
다음은 ablation 결과이다. Implicit Training은 ControlNet 학습 시에 VSD loss를 사용하는 경우이고, Denoising Training은 diff-instruct로 사전 학습시킨 1-step 모델에 대해 denoising loss로 ControlNet을 학습시킨 경우이다.

다음은 \(\log p (c \vert \textbf{x})\)를 직접 사용한 모델과 JDM을 비교한 결과이다.
