[논문리뷰] Image Restoration with Mean-Reverting Stochastic Differential Equations (IR-SDE)

ICML 2023. [Paper] [Page] [Github]
Ziwei Luo, Fredrik K. Gustafsson, Zheng Zhao, Jens Sjölund, Thomas B. Schön
Uppsala University
27 Jan 2023

Introduction

Diffusion model은 diffusion process를 모델링한 후 그 reverse의 학습을 기반으로 다양한 이미지 생성 task에서 인상적인 성능을 보여주었다. 일반적으로 사용되는 공식 중 확률적 미분 방정식(SDE)을 통해 정의된 diffusion model을 사용하는 공식을 채택한다. 이것은 SDE를 사용하여 순수한 noise 분포를 향해 이미지를 점진적으로 확산시킨 다음 해당 reverse-time SDE를 학습하고 시뮬레이션하여 샘플을 생성하는 것을 수반한다. 본질은 noisy한 데이터 분포의 score function을 추정하기 위해 신경망을 학습시키는 것이다.

Diffusion model은 최근 다양한 이미지 복원 task에 적용되었다. SR3는 저품질 이미지를 조건으로 하는 diffusion model을 학습시키는 반면, Repaint는 수정된 생성 프로세스와 함께 사전 학습된 unconditional model을 활용한다. 다른 연구들은 degradation과 그 파라미터가 테스트 시에 알려져 있다고 가정하여 이미지 복원을 inverse problem으로 명시적으로 취급한다. 이러한 방법은 모두 이미지를 순수한 noise로 확산시키는 표준 forward process를 사용한다. 따라서 reverse process는 높은 분산의 샘플링된 noise로 초기화되며, 이는 ground-truth 고품질 이미지의 불량한 복원을 초래할 수 있다. 많은 실험에서 diffusion model이 더 나은 지각 점수를 달성할 수 있지만 일부 픽셀/구조 기반 왜곡 기준 측면에서 만족스럽지 못한 성능을 보이는 경우가 많다.

본 논문은 이 문제를 해결하기 위해 mean-reverting SDE를 사용하여 이미지 복원 문제를 해결할 것을 제안한다. 위 그림에서 볼 수 있듯이 이것은 고품질 이미지에서 저품질 이미지로 이미지 degradation 자체를 모델링하도록 forward process를 조정한다. 해당 reverse-time SDE를 시뮬레이션하여 고품질 이미지를 복원할 수 있다. 중요한 것은 테스트 시 이미지 degradation을 모델링하는 데 task별 사전 지식이 필요하지 않고 학습을 위한 이미지 쌍 세트만 필요하다는 것이다.

Method

본 논문이 제안한 이미지 복원 접근법의 핵심 아이디어는 mean-reverting SDE를 신경망 학습을 위한 최대 likelihood 목적 함수와 결합하는 것이다. 따라서 이를 이미지 복원 확률 미분 방정식(IR-SDE)이라고 한다.

1. Forward SDE for Image Degradation

Score function이 수치적으로 다루기 쉬운 SDE의 특수한 경우를 다음과 같이 구성한다.

\[\begin{equation} dx = \theta_t (\mu - x) dt + \sigma_t dw \end{equation}\]

여기서 $\mu$는 상태 평균이고 $\theta_t$, $\sigma_t$는 mean-reversion의 속도와 확률적 변동성을 각각 특성화하는 양의 파라미터이다. $\theta_t$와 $\sigma_t$를 선택할 때 많은 자유가 있으며 이 선택은 결과 복원 성능에 상당한 영향을 미칠 수 있다.

일반적으로 $\mu$와 시작 상태 $x(0)$는 서로 다른 이미지 쌍으로 설정할 수 있다. 그런 다음 위의 forward SDE는 일종의 noise 보간으로 하나의 이미지를 다른 이미지로 전송한다. 이미지 degradation을 수행하기 위해 $x(0)$와 $\mu$를 각각 ground-truth 고품질(HQ) 이미지와 degrade된 저품질(LQ) 이미지로 둔다. 따라서 $\mu$는 $x(0)$에 의존하지만 (동일한 물체 또는 장면의 쌍을 이룬 HQ/LQ 이미지이므로) $x(0)$는 브라운 운동과 독립적이며 따라서 SDE는 여전히 유효하다.

SDE가 closed-form 해를 갖기 위해

\[\begin{equation} \frac{\sigma_t^2}{\theta_t} = 2 \lambda^2 \end{equation}\]

로 설정한다. 여기서 $\lambda^2$은 고정 분산이다. 그러면 임의의 시간 $s < t$에서의 시작 상태 $x(s)$가 주어지면 SDE의 해는 다음과 같다.

\[\begin{equation} x(t) = \mu + (x(s) - \mu) \exp(- \bar{\theta}_{s:t}) + \int_s^t \sigma_z \exp(- \bar{\theta}_{z:t}) dw(z) \\ \textrm{where} \quad \bar{\theta}_{s:t} := \int_s^t \theta_z dz \end{equation}\]

여기서 \(\bar{\theta}_{s:t}\)는 알고 있는 값이며, transition kernel

\[\begin{equation} p(x(t) \vert x(s)) = \mathcal{N} (x(t) \vert m_{s:t} (x(s)) v_{s:t}) \end{equation}\]

는 평균 $m_{s:t}$와 분산 $v_{s:t}$가

\[\begin{aligned} m_{s:t} (x(s)) &:= \mu + (x(s) - \mu) \exp(-\bar{\theta}_{s:t}) \\ v_{s:t} &:= \int_t^s \sigma_z^2 \exp(-2 \bar{\theta}_{s:t}) dz = \lambda^2 (1 - \exp(-2 \bar{\theta}_{s:t})) \end{aligned}\]

로 주어진 가우시안 분포이다.

시작 상태가 $x(0)$일 때 표기법을 단순화하기 위해 \(\bar{\theta}_{0:t}\), $m_{0:t}$, $v_{0:t}$를 각각 \(\bar{\theta}_t\), $m_t$, $v_t$로 대체한다. 그러면 주어진 초기 상태를 조건으로 하는 임의의 시간 $t$에서 $x(t)$의 분포는 다음과 같다.

\[\begin{aligned} p_t (x) &= \mathcal{N} (m_t (x), v_t) \\ m_t (x) &:= \mu + (x(0) - \mu) \exp (- \bar{\theta}_t) \\ v_t &:= \lambda^2 (1 - \exp (- \bar{\theta}_t)) \end{aligned}\]

$t \rightarrow \infty$일 때 평균 $m_t$는 저품질 이미지 $µ$로 수렴하고 분산 $v_t$는 $\lambda^2$으로 수렴한다. 즉, forward SDE는 고품질 이미지를 고정된 Gaussian noise가 있는 저품질 이미지로 확산시킨다.

2. Reverse-Time SDE for Image Restoration

최종 상태 $x(T)$에서 고품질 이미지를 복구하기 위해 SDE를 reverse하여 IR-SDE를 도출한다.

\[\begin{equation} dx = [\theta_t (\mu - x) - \sigma_t^2 \nabla_x \log p_t (x)] dt + \sigma_t d \hat{w} \end{equation}\]

테스트 시에 유일하게 알려지지 않은 부분은 시간 $t$에서의 주변 분포의 score $\nabla_x \log p_t(x)$이다. 그러나 학습 중에는 고품질 이미지 $x(0)$의 ground-truth를 사용할 수 있으므로 조건부 score $\nabla_x \log p_t(x \vert x(0))$를 추정하도록 신경망을 학습할 수 있다. 구체적으로 ground-truth score를 다음과 같이 계산할 수 있다.

\[\begin{equation} \nabla_x \log p_t (x \vert x(0)) = - \frac{x(t) - m_t(x)}{v_t} \end{equation}\]

이는 깨끗한 이미지와 noisy한 이미지를 기반으로 ground-truth score를 계산하는 표준 denoising score matching과 유사하다. 또한

\[\begin{equation} x(t) = m_t(x) + \sqrt{v_t} \epsilon_t, \quad \epsilon_t \sim \mathcal{N}(0, I) \end{equation}\]

를 다시 parameterize하면 다음과 같이 noise 측면에서 직접 score를 얻을 수 있다.

\[\begin{equation} \nabla_x \log p_t (x \vert x(0)) = - \frac{\epsilon_t}{\sqrt{v_t}} \end{equation}\]

그런 다음 상태 $x$, 조건 $\mu$, 시간 $t$를 모두 취하는 조건부 신경망 \(\tilde{\epsilon}_\phi (x_t, \mu, t)\)를 사용하여 noise를 근사하는 일반적인 관행을 따르고 순수한 noise를 입력하고 출력한다. 이러한 네트워크는 DDPM에서 사용되는 것과 유사한 다음 목적 함수로 학습시킬 수 있다.

\[\begin{equation} L_\gamma (\phi) := \sum_{t=1}^T \gamma_t \mathbb{E} [\| \tilde{\epsilon}_\phi (x_t, \mu, t) - \epsilon_t \|] \end{equation}\]

여기서 $\gamma_1, \cdots, \gamma_T$는 양의 가중치이고 \(\{x_i\}_{i=0}^T\)는 diffusion process의 이산화(discretization)를 나타낸다. 일단 학습되면 $x_T$를 샘플링하고 네트워크 \(\tilde{\epsilon}_\phi\)를 사용하여 Euler-Maruyama와 같은 수치적 방법으로 IR-SDE를 반복적으로 풀어 고품질 이미지를 생성할 수 있다.

3. Maximum Likelihood Learning

위의 목적 함수가 score를 학습하는 간단한 방법이라는 사실에도 불구하고 경험적으로 이미지 복원에서 발생하는 복잡한 degradation에 적용할 때 학습이 종종 불안정해진다. 저자들은 이러한 어려움이 주어진 시간에 순간적인 noise를 학습하려는 시도에서 비롯된 것이라고 추측한다. 따라서 주어진 고품질 이미지 $x_0$에서 최적의 궤적 $x_{1:T}$를 찾으려는 아이디어에 기반하여 최대 likelihood 목적 함수를 제안한다. 이 목적 함수는 보다 정확한 score function을 학습하기 위해 제안된 것이 아니며, 대신 학습을 안정화하고 보다 정확한 이미지를 복구하는 데 사용된다.

구체적으로, 다음과 같이 분해할 수 있는 likelihood $p(x_{1:T} \vert x_0)$를 최대화하려고 한다.

\[\begin{equation} p(x_{1:T} \vert x_0) = p(x_T \vert x_0) \prod_{t=2}^T p(x_{t-1} \vert x_t, x_0) \\ p(x_T \vert x_0) = \mathcal{N} (x_T; m_T (x_0), v_T) \end{equation}\]

여기서 $p(x_T \vert x_0)p(x_T \vert x_0)$는 저품질 이미지 분포이다. 그런 다음 베이즈 정리로 reverse transition을 유도할 수 있다.

\[\begin{equation} p(x_{t-1} \vert x_t, x_0) = \frac{p(x_t \vert x_{t-1}, x_0) p(x_{t-1} \vert x_0)}{p (x_t \vert x_0)} \end{equation}\]

모든 분포는 계산할 수 있는 가우시안이므로 negative log-likelihood를 최소화하는 최적의 reverse 상태를 직접 찾는 것이 자연스럽다.

\[\begin{equation} x_{t-1}^\ast = \underset{x_{t-1}}{\arg \min} [- \log p(x_{t-1} \vert x_t, x_0)] \end{equation}\]

여기서 $x_{t-1}^\ast$는 $x_t$에서 reverse된 이상적인 상태이다. 간단하게

\[\begin{equation} \theta'_t = \int_{t-1}^t \theta_z dz \end{equation}\]

라고 표기하자. 위의 목적 함수를 풀면 IR-SDE의 최적의 해는 다음과 같다.

\[\begin{aligned} x_{t-1}^\ast =\;& \frac{1 - \exp(-2 \bar{\theta}_{t-1})}{1 - \exp(-2 \bar{\theta}_t)} \exp(- \theta'_t) (x_t - \mu) \\ &+ \frac{1 - \exp(-2 \theta'_{t-1})}{1 - \exp(-2 \bar{\theta}_t)} \exp(- \bar{\theta}_{t-1}) (x_0 - \mu) + \mu \end{aligned}\]

이 목적 함수를 사용하여 DDPM의 평균을 도출할 수도 있다. 그런 다음 noise 네트워크 \(\tilde{\epsilon}_\phi (x_t, \mu, t)\)를 최적화하여 IR-SDE를 최적의 궤적으로 reverse하도록 선택한다.

\[\begin{equation} J_\gamma (\phi) := \sum_{t=1}^T \gamma_t \mathbb{E} [\| x_t - (dx_t)_{\tilde{\epsilon}_\phi} - x_{t-1}^\ast \|] \end{equation}\]

여기서 \((dx)_{\tilde{\epsilon}_\phi}\)는 IR-SDE에서 score를 \(\tilde{\epsilon}_\phi\)로 예측한 것이다.

\[\begin{equation} \int_0^t \sigma_s d \hat{w}(s) \end{equation}\]

의 기댓값이 0이므로 \((dx)_{\tilde{\epsilon}_\phi}\)의 drift 부분만 고려하면 된다.

Experiment

1. Image Deraining

다음은 Rain100H test set에서 이미지 deraining을 수행한 정량적 결과를 비교한 표이다.

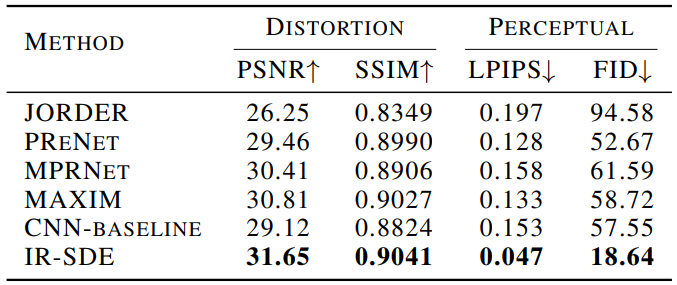
다음은 Rain100L test set에서 이미지 deraining을 수행한 정량적 결과를 비교한 표이다.

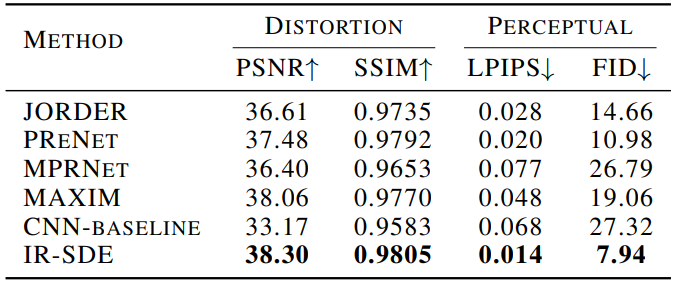
다음은 IR-SDE와 다른 deraining 방법들의 시각적 결과를 비교한 것이다.

2. Image Deblurring

다음은 GoPro test set에서 이미지 deblurring을 수행한 정량적 결과를 비교한 표이다.

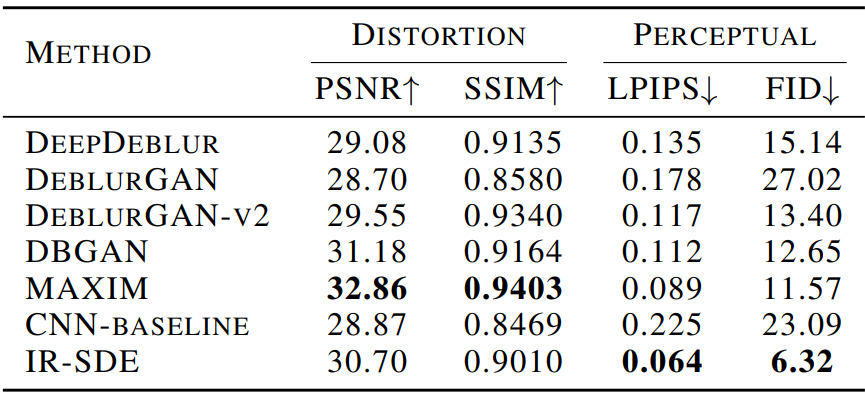
다음은 IR-SDE와 다른 deblurring 방법들의 시각적 결과를 비교한 것이다.

3. Gaussian Image Denoising

SDE의 Wiener process는 Gaussian process이다. 따라서 모든 $t$에서 $\mu = x_0$로 설정하여 denoising 계산을 더 적은 timestep으로 수행할 수 있다. 이 방법을 Denoising-SDE라고 부른다. 또한, 이미지에 Gaussian noise만 존재하기 때문에, SDE와 동일한 주변 확률을 공유하지만 Wiener process에서 추가 noise를 도입하지 않고 denoising을 수행할 수 있는 Denoising-ODE을 유도하는 것이 타당하다.

\[\begin{equation} dx = \bigg[ \theta_t (\mu - x) - \frac{1}{2} \sigma_t^2 \nabla_x \log p_t (x) \bigg] dt \end{equation}\]

다음은 noise 레벨 $\sigma = 25$에서 이미지 denoising을 수행한 정량적 결과를 비교한 표이다.

IR-SDE의 전체 step은 100이지만, Denoising-SDE/ODE는 22 step만이 필요하다.

다음은 다른 denoising 방법들과 시각적 결과를 비교한 것이다.

4. Qualitative Experiments

다음은 본 논문의 방법을 사용한 DDPM을 Gaussian image denoising, super-resolution, face inpainting에서 비교한 결과이다.

Super-Resolution

다음은 DIV2K validation dataset에서 super-resolution의 시각적 결과를 비교한 것이다.

Face Inpainting

다음은 CelebA-HQ 데이터셋에서 inpainting의 시각적 결과를 비교한 것이다.

Dehazing

다음은 SOTS indoor dataset에서 dehazing의 시각적 결과를 비교한 것이다.

Discussion

1. Reverse-Time Restoration Process

다음은 reverse-time deblurring process를 시각화한 것이다.

다음은 위의 복원 과정에서의 성능을 timestep에 대하여 나타낸 그래프이다.

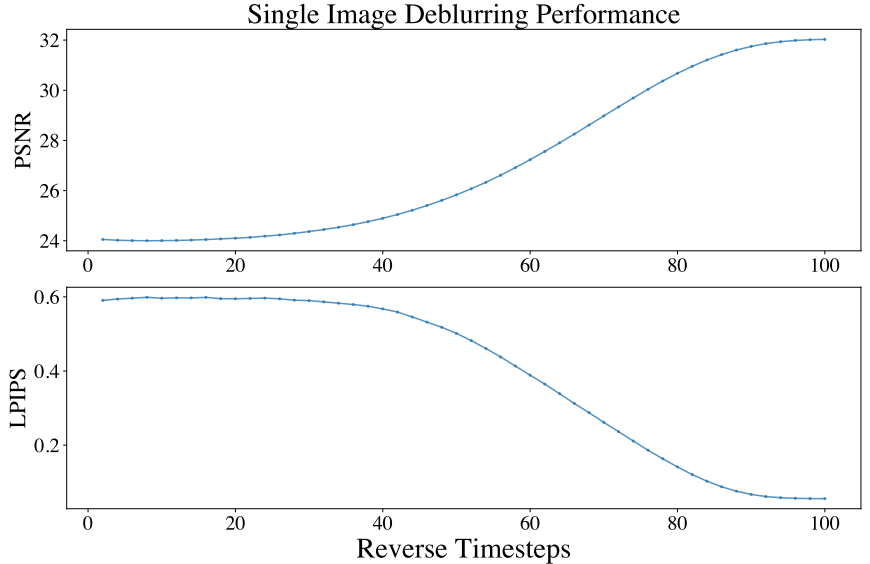
2. Maximum Likelihood Objective

다음은 다양한 task에서의 학습 곡선이다.

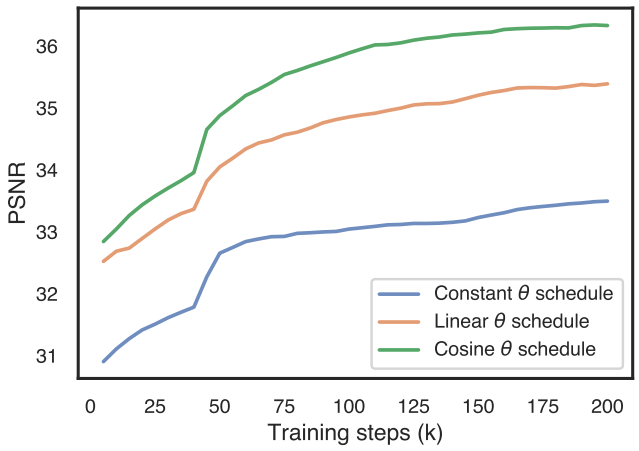
3. Time-Varying Theta Schedules

다음은 다양한 $\theta$ schedule에 대한 학습 곡선이다.

4. Limitations

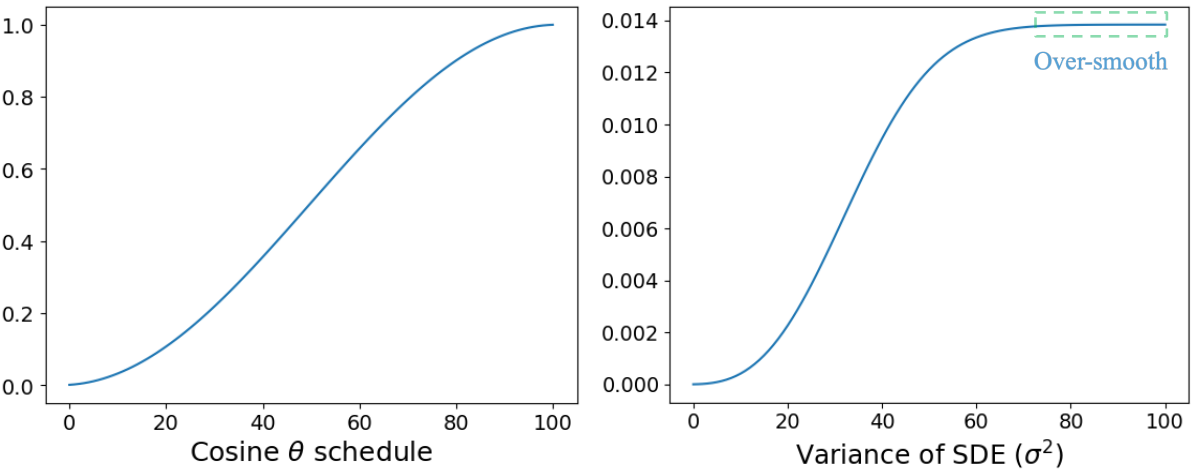
위 그래프에서 볼 수 있듯이 $v_t$에 대한 지수 항은 마지막 몇 step에서 지나치게 부드러운 분산 변화로 이어진다. 해당 영역에서 $(x_t, x_{t-1})$은 매우 유사한 모양을 가지므로 특히 maximum likelihood loss를 사용할 때 학습이 어렵다.