[논문리뷰] InstaFlow: One Step is Enough for High-Quality Diffusion-Based Text-to-Image Generation
ICLR 2024. [Paper] [Github]
Xingchao Liu, Xiwen Zhang, Jianzhu Ma, Jian Peng, Qiang Liu
University of Texas at Austin | Helixon Research
12 Sep 2023
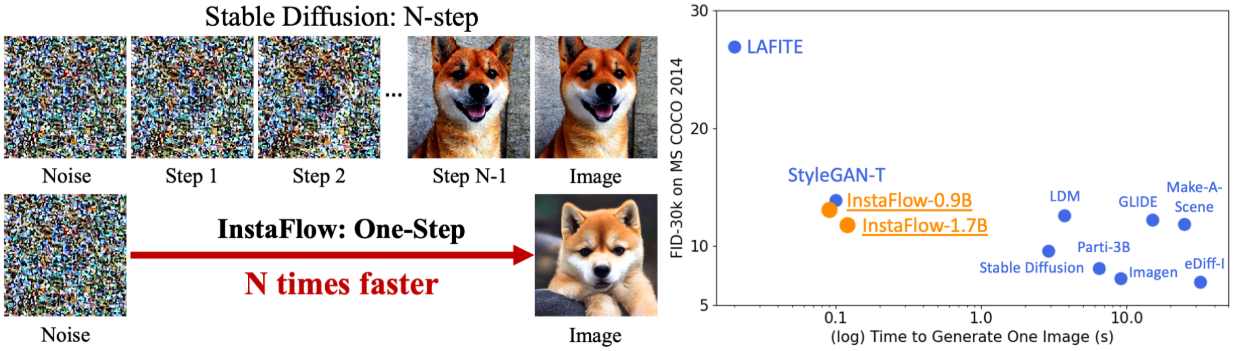
Introduction
최신 text-to-image (T2I) 생성 모델은 인상적인 생성 품질에도 불구하고 과도한 inference 시간과 계산 소비로 인해 어려움을 겪는 경우가 많다. 이는 모델의 대부분이 autoregressive 모델이거나 diffusion model이라는 사실에 기인할 수 있다. 예를 들어 Stable Diffusion (SD)은 괜찮은 이미지를 생성하는 데 20 step 이상이 필요하다. 결과적으로 이전 연구들은 필요한 샘플링 step을 줄이고 inference를 가속화하기 위해 knowledge distillation을 사용하였다. 이러한 방법은 작은 step에서는 어려움을 겪는다. 특히, one-step diffusion model은 아직 개발되지 않았다.
본 논문에서는 SD에서 파생된 새로운 one-step 생성 모델을 제시하였다. 저자들은 SD의 간단한 distillation이 완전한 실패로 이어진다는 것을 관찰했다. 주요 문제는 noise와 이미지의 좋지 못한 결합에서 비롯되며, 이는 distillation 프로세스를 크게 방해한다. 이 문제를 해결하기 위해 몇 개 또는 하나의 Euler step으로 수정 가능한 직선 flow model을 학습하는 Rectified Flow를 활용한다. Rectified flow는 잠재적으로 곡선인 flow model과 데이터 분포를 매칭시키는 것에서 시작된다. 그런 다음 flow의 궤적을 직선화하기 위해 고유한 Reflow 절차를 사용하여 noise 분포와 이미지 분포 사이의 전송 비용을 줄인다. 이러한 커플링의 개선으로 인해 distillation이 크게 촉진된다. 본 논문에서는 대규모 T2I 모델을 1-flow로 취하고 reflow를 통해 이를 직선화하는 데 중점을 두었다.
Methods
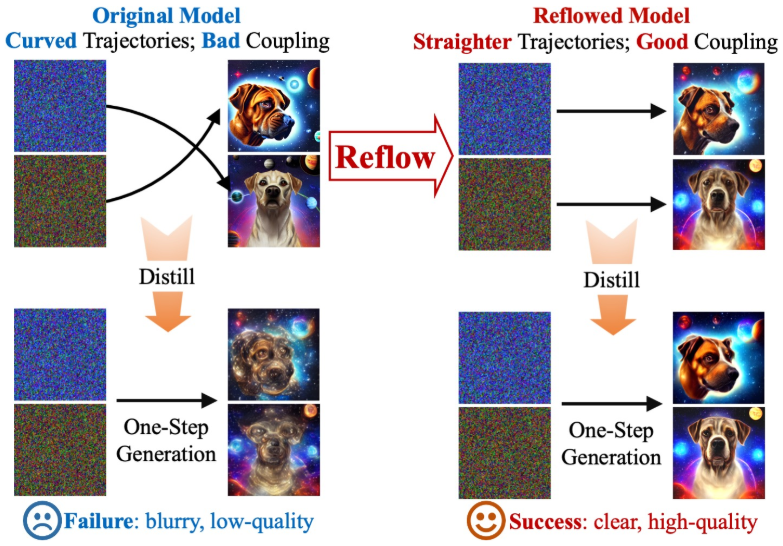
1. Rectified Flow and Reflow
Rectified Flow는 생성 모델링 및 도메인 전송을 위한 통합 ODE 기반 프레임워크이다. 이는 $\mathbb{R}^d$의 두 분포 $\pi_0$와 $\pi_1$ 사이의 매핑 $T$를 학습하기 위한 접근 방식이다. 이미지 생성에서 $\pi_0$는 일반적으로 Gaussian 분포이고 $\pi_1$은 이미지 분포이다.
Rectified Flow는 ODE 또는 flow model을 통해 $\pi_0$를 $\pi_1$으로 변환하는 방법을 학습한다.
\[\begin{equation} \frac{dZ_t}{dt} = v (Z_t, t), \quad \textrm{ initialized from } Z_0 \sim \pi_0, \textrm{ such that } Z_1 \sim \pi_1 \end{equation}\]여기서 $v : \mathbb{R}^d \times [0, 1] \rightarrow \mathbb{R}^d$는 간단한 MSE를 최소화하여 학습된 속도장이다.
\[\begin{equation} \min_v \mathbb{E}_{(X_0, X_1) \sim \gamma} \bigg[ \int_0^1 \| \frac{d}{dt} X_t - v (X_t, t) \|^2 dt \bigg], \quad \textrm{with} \quad X_t = \phi (X_0, X_1, t) \end{equation}\]$X_t$는 $X_0$와 $X_1$ 사이의 시간으로 미분 가능한 interpolation이며,
\[\begin{equation} \frac{d}{dt} X_t = \partial_t \phi (X_0, X_1, t) \end{equation}\]이다. $\gamma$는 $(\pi_0, \pi_1)$의 임의의 커플링이다. 일반적으로 $v$는 신경망으로 parameterize되고 stochastic gradient method을 사용하여 대략적으로 풀 수 있다. $X_t$를 바꾸면 다른 알고리즘이 생성된다. 일반적으로 사용되는 DDIM과 probability flow ODE는 $X_t = \alpha_t X_0 + \beta_t X_1$에 해당한다. 그러나 rectified flow는 더 간단한 선택을 제안했다.
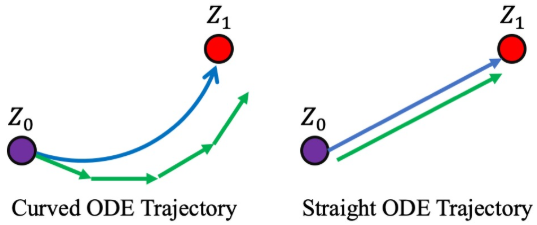
\[\begin{equation} X_t = (1 - t) X_0 + t X_1 \quad \implies \quad \frac{d}{dt} X_t = X_1 - X_0 \end{equation}\]직선 궤적은 빠른 inference에 중요한 역할을 한다.
직선 flow는 빠른 생성을 가능하게 한다.
실제로 ODE는 수치적 방법을 사용하여 근사화해야 한다. 가장 일반적인 접근법은 forward Euler method이다.
여기서 step 크기는 $\epsilon = 1/N$이고 $N$ step으로 시뮬레이션을 완료한다. $N$이 클수록 ODE에 더 잘 근접하지만 계산 비용이 높아진다. 빠른 시뮬레이션을 위해서는 작은 $N$으로 정확하고 빠르게 시뮬레이션할 수 있는 ODE를 학습하는 것이 바람직하다. 따라서 궤적이 직선인 ODE가 필요하다. 다음과 같은 경우 ODE가 직선(균일한 속도)이라고 말한다.
\[\begin{equation} Z_t = t Z_1 + (1 - t) Z_0 = Z_0 + t v(Z_0, 0), \quad t \in [0, 1] \end{equation}\]이 경우 $N = 1$의 Euler method는 완벽한 시뮬레이션을 생성한다. 따라서 ODE 궤적을 직선화하는 것은 inference 비용을 줄이는 데 필수적인 방법이다.
텍스트 조건부 reflow를 통해 텍스트 조건부 probability flow 직선화
Reflow는 marginal distribution을 수정하지 않고 rectified flow의 궤적을 직선화하여 inference 시 빠른 시뮬레이션을 가능하게 하는 반복적인 절차이다. T2I 생성에서 속도장 $v$는 해당 이미지를 생성하기 위해 입력 텍스트 프롬프트 $\mathcal{T}$에 추가적으로 의존해야 한다. 본 논문은 다음과 같은 새로운 텍스트 조건부 reflow 목적 함수를 제안하였다.
\[\begin{equation} v_{k+1} = \underset{v}{\arg \min} \mathbb{E}_{X_0 \sim \pi_0, \mathcal{T} \sim \mathcal{D}_\mathcal{T}} \bigg[ \int_0^1 \| (X_1 - X_0) - v (X_t, t \vert \tau) \|^2 dt \bigg] \\ \quad \textrm{with} \quad X_1 = \textrm{ODE} [v_k] (X_0 \; \vert \; \mathcal{T}) = X_0 + \int_0^1 v_k (X_t, t \; \vert \; \mathcal{T}) dt \quad \textrm{and} \quad X_t = t X_1 + (1 - t) X_0 \end{equation}\]\(\mathcal{D}_\mathcal{T}\)는 텍스트 프롬프트 데이터셋이다. $v_{k+1}$은 동일한 rectified flow 목적 함수를 사용하여 학습되지만 $\textrm{ODE}[v_k]$에서 구성된 $(X_0, X_1)$ 쌍의 linear interpolation을 사용한다.
Reflow의 주요 특성은 궤적을 직선화하고 매핑의 전송 비용을 줄이면서 최종 분포를 보존한다는 것이다.
- $\textrm{ODE}[v_{k+1}] (X_0 \; \vert \; \mathcal{T})$와 $\textrm{ODE}[v_k] (X_0 \; \vert \; \mathcal{T})$의 분포는 일치한다. 따라서 $v_k$가 올바른 이미지 분포 $\pi_1$을 생성하면 $v_{k+1}$도 그렇다.
- $\textrm{ODE}[v_{k+1}]$의 궤적은 $\textrm{ODE}[v_k]$의 궤적보다 직선적인 경향이 있다. 이는 $\textrm{ODE}[v_{k+1}]$를 시뮬레이션하는 데 $\textrm{ODE}[v_k]$보다 더 작은 step $N$이 필요함을 의미한다.
- $v_k$가 reflow의 고정점(fixed point)이면, 즉 $v_{k+1} = v_k$이면 $\textrm{ODE}[v_k]$는 정확히 직선이어야 한다.
- $(X_0, \textrm{ODE}[v_{k+1}] (X_0 \; \vert \; \mathcal{T}))$는 $(X_0, \textrm{ODE}[v_k] (X_0 \; \vert \; \mathcal{T}))$보다 convex transport cost가 더 낮다는 점에서 더 나은 커플링을 형성한다. 즉, 모든 convex function $c: \mathbb{R}^d \rightarrow \mathbb{R}$에 대하여 다음을 만족한다.
이는 student 네트워크가 새로운 커플링을 더 쉽게 배울 수 있음을 의미한다.
본 논문에서는 $v_1$을 Stable Diffusion의 속도장 \(v_\textrm{SD}\)로 설정하고 $k$-Rectified Flow를 $v_k$라 한다 ($k \ge 2$).
텍스트 조건부 distillation
이론적으로 정확히 직선 궤적을 갖는 ODE를 얻으려면 무한한 reflow step이 필요하다. 그러나 너무 많은 step을 reflow하는 것은 높은 계산 비용과 최적화 및 통계적 오차의 누적으로 인해 실용적이지 않다. 다행스럽게도 ODE의 궤적은 1~2 step의 refloW만으로도 거의 직선이 된다. 이러한 거의 직선인 ODE를 사용한 distillation을 통해 one-step 모델의 성능을 향상시킬 수 있다.
\[\begin{equation} \tilde{v}_k = \underset{v}{\arg \min} \mathbb{E}_{X_0 \sim \pi_0, \mathcal{T} \sim \mathcal{D}_\mathcal{T}} [\mathbb{D} (\textrm{ODE} [v_k] (X_0 \; \vert \; \mathcal{T}), X_0 + v(X_0 \; \vert \; \mathcal{T}))] \end{equation}\]이미지 간의 미분 가능한 similarity loss $\mathbb{D}(\cdot, \cdot)$를 최소화하여 $X_0$에서 $\textrm{ODE}[v_k] (X_0 \; \vert \; \mathcal{T})$로의 매핑을 압축하는 단일 Euler step $x + v(x \; \vert \; \mathcal{T})$를 학습시킨다.
Distillation과 reflow는 상충되지 않는다.
Distillation은 $X_0$에서 $\textrm{ODE}[v_k] (X_0 \; \vert \; \mathcal{T})$로의 매핑을 정직하게 근사화하려고 시도한다. 반면, reflow는 낮은 convex transport cost로 인해 더 규칙적이고 부드러울 수 있는 새로운 매핑 $\textrm{ODE}[v_{k+1}] (X_0 \; \vert \; \mathcal{T})$를 생성한다. Reflow는 distillation 전 선택적 단계이며, 서로 효과가 겹치지 않는다. 실제로 distillation을 적용하기 전에 매핑 $\textrm{ODE}[v_k] (X_0 \; \vert \; \mathcal{T})$를 충분히 규칙적이고 매끄럽게 만들기 위해 reflow를 적용하는 것이 필수적이다.
텍스트 조건부 rectified flow를 위한 classifier-free guidance 속도장
Classifier-free guidance는 SD의 생성 품질에 상당한 영향을 미친다. 저자들은 classifier-free guidance와 유사한 효과를 내기 위해 학습된 텍스트 조건부 rectified flow에 대해 다음과 같은 속도장을 제안하였다.
\[\begin{equation} v^\alpha (Z_t, t \; \vert \; \mathcal{T}) = \alpha v(Z_t, t \; \vert \; \mathcal{T}) + (1 - \alpha) v (Z_t, t \; \vert \; \textrm{NULL}) \end{equation}\]여기서 $\alpha$는 샘플 다양성과 생성 품질을 절충한다. $\alpha = 1$일 때 $v^\alpha$는 원래 속도장이 된다.
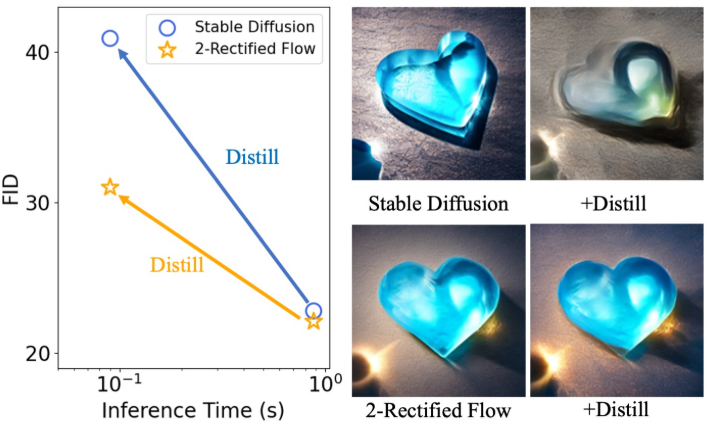
Preliminary Results: Reflow is the Key to Improve Distillation
다음은 (왼쪽) MS COCO 2017에서의 inference 시간과 FID를 비교한 그래프와 (오른쪽) 동일한 랜덤 noise와 텍스트 프롬프트로 생성된 이미지들이다.
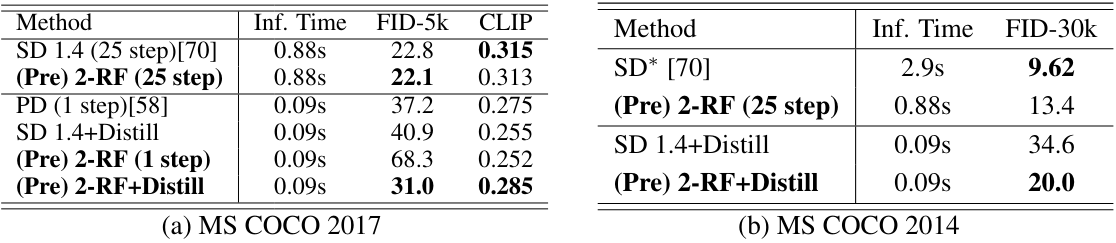
다음은 MS COCO 2017와 MS COCO 2014에서 성능을 비교한 표이다.
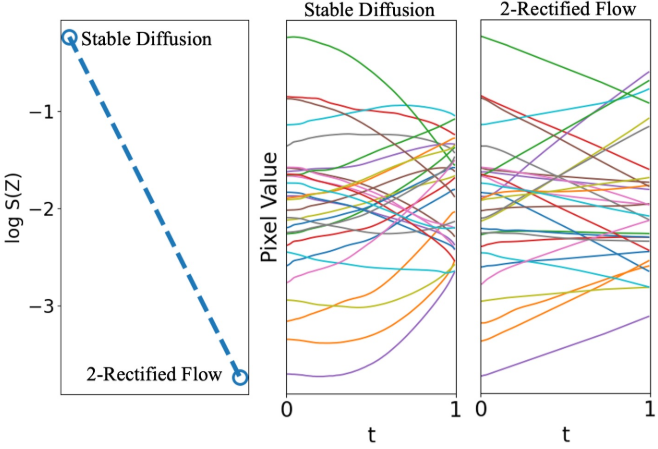
다음은 rectified flow의 직선화 효과를 비교한 그래프이다.
다음은 SD와 2-Rectified Flow의 생성 결과를 비교한 것이다. $N$은 inference step의 수이다.

InstaFlow: Scaling Up for Better One-Step Generation
다음은 InstaFlow-0.9B에서 one-step으로 생성한 결과들이다.

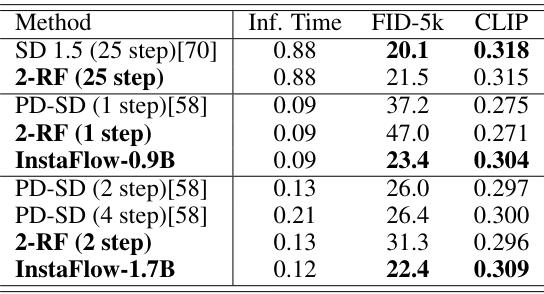
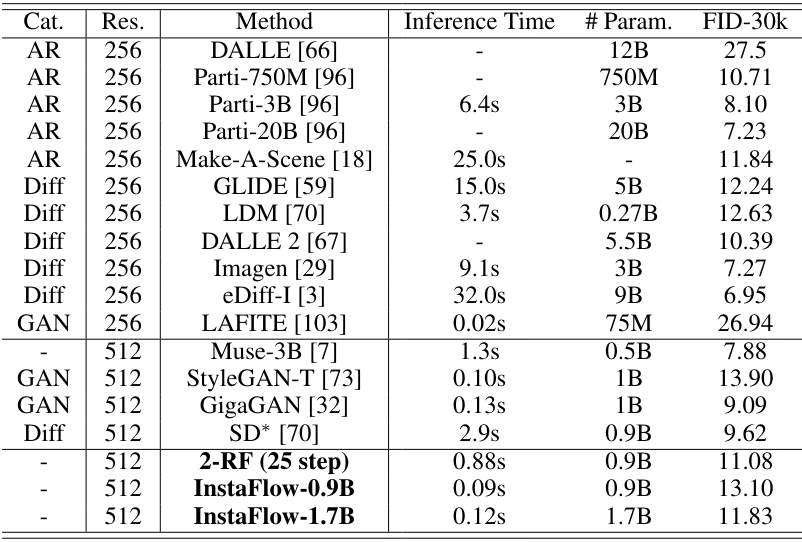
다음은 (왼쪽) MS COCO 2017와 (오른쪽) MS COCO 2014에서 성능을 비교한 표이다.
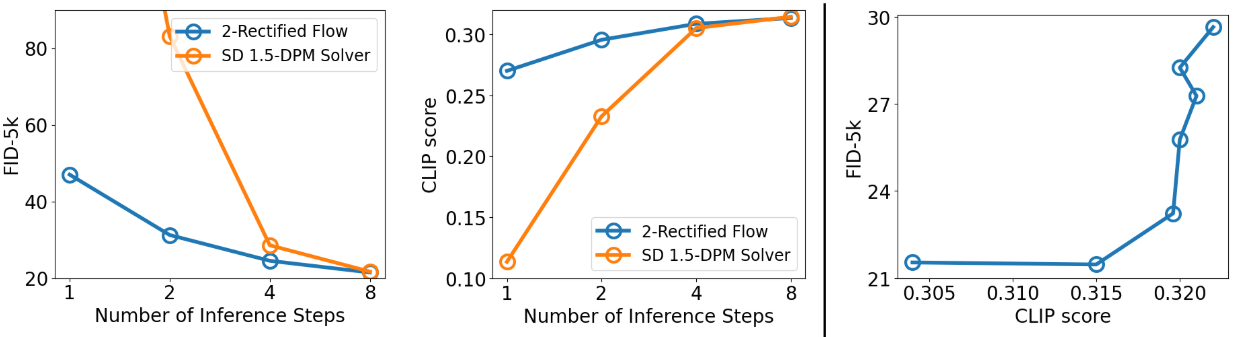
다음은 (왼쪽) SD 1.5-DPM Solver와 2-Rectified Flow의 성능을 비교한 그래프와 (오른쪽) 2-Rectified Flow의 guidance scale에 따른 trade-off 그래프이다.
다음은 SDXL-Refiner로 one-step model을 개선시킨 결과를 개선 전과 비교한 결과이다.

Limitations
다음은 failure case의 예시이다. InstaFlow는 텍스트 프롬프트의 복잡한 구성으로 인해 문제가 발생할 수 있다.
