[논문리뷰] ∞-Diff: Infinite Resolution Diffusion with Subsampled Mollified States

ICLR 2024. [Paper] [Github]
Sam Bond-Taylor, Chris G. Willcocks
Department of Computer Science, Durham University
31 Mar 2023

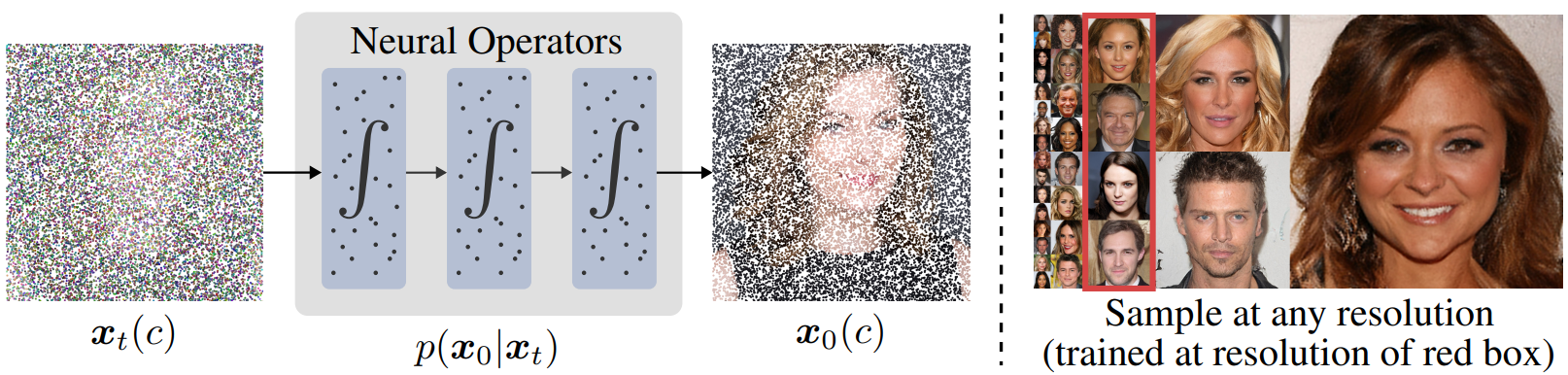
Introduction

Diffusion model을 더 높은 해상도로 확장하는 것은 저해상도 이미지를 반복적으로 업샘플링하고 압축된 latent space에서 작동하는 방법을 포함하는 다양한 최근 연구의 주제였다. 심층 신경망은 일반적으로 데이터가 고정된 균일 격자로 표현될 수 있다고 가정하지만 신호는 종종 연속적이다. 따라서 이러한 접근 방식은 해상도에 따라 제대로 확장되지 않는다. 이 문제를 해결하기 위해 neural field가 제안되었다. 여기에서 좌표를 강도(ex. 픽셀 값)에 직접 매핑하여 데이터를 표현하고, 이를 통해 parameterization을 데이터 해상도와 독립적으로 만든다.

데이터를 해상도에 대하여 더 잘 확장할 수 있는 함수로 표현하려고 시도하는 여러 생성 모델이 개발되었다. 이러한 접근 방식은 모두 neural field를 기반으로 하지만 neural field는 본질적으로 좌표 간에 독립적이기 때문에 전체 정보를 제공하기 위해 압축된 유한 크기의 latent 벡터에 대한 네트워크 컨디셔닝에 의존한다.

기본 데이터를 분해능으로 더 잘 확장할 수 있는 함수로 표현하려고 시도하는 여러 생성 모델이 개발되었다. 이러한 접근 방식은 모두 신경 필드를 기반으로 하지만 신경 필드는 본질적으로 좌표 간에 독립적이기 때문에 이러한 접근 방식은 전체 정보를 제공하기 위해 압축된 유한 크기 잠재 벡터에 대한 네트워크 컨디셔닝에 의존한다. 이와 같은 압축된 latent 기반 neural field 접근 방식은 데이터의 noise를 효과적으로 제거하기 위해 글로벌한 정보와 로컬한 정보를 모두 유지해야 하는 diffusion model을 parameterize하는 데 효과적으로 사용할 수 없다. 본 논문에서는 다음과 같은 문제를 해결하기 위해 ∞-Diff를 제안한다.

Infinite Dimensional Diffusion Models

데이터가 균일한 격자에 있다고 가정하는 이전의 diffusion model과 달리 데이터가 연속 함수라고 가정한다. 이 경우, 데이터 포인트 $x \sim q$는 dual space $\mathcal{H}, q \in \mathcal{H}^\ast$, 즉 $q : \mathbb{H} \rightarrow \mathbb{R}$에서 정의된 확률 분포에서 샘플링된 도메인 $\mathbb{R}^d$를 갖는 분리 가능한 Hilbert space $\mathcal{H}$에 정의된 함수다. 단순화를 위해 다른 space에 적용될 수 있지만 $\mathcal{H}$가 $[0, 1]^n$에서 $\mathbb{R}^d$까지 $L^2$ 함수의 space인 경우를 고려한다.

1. White Noise Diffusion

Diffusion model을 무한 차원으로 확장하기 위한 한 가지 고려 사항은 각 좌표가 독립적이고 동일하게 분포된 가우시안 확률 변수인 연속적인 white noise를 사용하는 것이다. 즉, Dirac delta 함수 $\delta$를 사용하여 공분산 연산자가 $C_I (z(s), z(s’)) = \delta (s − s’)$인 $\mathcal{N} (0, C_I)$를 사용한다. Transition 밀도는 다음과 같이 무한 차원으로 확장될 수 있다.

\[\begin{equation} q(x_t \vert x_{t-1}) = \mathcal{N} (x_t; \sqrt{1-\beta_t} x_{t-1}, \beta_t C_I) \\ p(x_{t-1} \vert x_t) = \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \Sigma_\theta (x_t, t)) \end{equation}\]

여기서 유한 차원의 경우와 유사하게 $\Sigma_\theta (x_t, t) = \sigma_t^2 C_I$로 고정한다. 유한 차원 접근법과 가장 유사하지만, 이 방법은 이와 같이 정의된 white noise가 $\mathcal{H}$에 있지 않고 $x_t$에도 없기 때문에 문제가 있다. 그러나 실제로 무한 차원에서 계산적으로 작동할 수 없으며 대신 orthogonal projection을 통해 연속적인 space의 discretisation에서 작동한다. 이 경우 norm은 유한하다. 즉, 각 $x$가 $n$ 공간 차원을 갖는 경우 좌표 공간은 $D = [0, 1]^n$이다. $m$개의 좌표 $\mathbf{c} \in \binom{D}{m}$을 샘플링하여 $x(\mathbf{c}) \in \mathbb{R}^{m \times d}$로 $x$를 discretise한다. 따라서 각 함수를 근사하는 Monte-Carlo에 의해 loss

\[\begin{aligned} \mathcal{L} &= \sum_{t \ge 1} \mathbb{E}_q [D_\textrm{KL} (q (x_{t-1} \vert x_t, x_0) \;\|\; p(x_{t-1} \vert x_t))] \\ &= \sum_{t \ge 1} \mathbb{E}_q \bigg[ \frac{1}{2 \sigma_t^2} \| \tilde{\mu}_t (x_t, x_0) - \mu_\theta (x_t, t) \|_2^2 \bigg] \end{aligned}\]

을 근사할 수 있다. 여기서 $\tilde{\mu}$와 $\mu_\theta$는 closed form 또는 근사의 계산을 통해 부분집합에서 작동할 수 있다고 가정한다.

\[\begin{equation} \mathcal{L} = \sum_{t=1}^T \mathbb{E}_{q(x_t)} \mathbb{E}_{c \sim U(\binom{D}{m})} [\| \tilde{\mu} (x_t (c), x_0 (c)) - \mu_\theta (x_t (c), t) \|_2^2 ] \end{equation}\]

2. Smoothing States with Mollified Diffusion

White noise로 생성 모델을 구축할 수 있지만 실제로는 입력이 $\mathcal{H}$에 있다고 가정하는 신경망 아키텍처를 사용할 수 있다. 이 때문에 mollifier $T$ (ex. trunctated Gaussian kernel)를 사용하여 함수를 convolution하여 부드러운 함수로 매끄럽지 않은 입력 space를 근사하는 대체 diffusion process를 제안한다. 이러한 방식으로 white noise를 convolution하면 Gaussian random field가 생성된다. 정규 분포된 변수 $x \sim \mathcal{N} (\mu, C)$의 선형 변환 $y = T x + b$가 $y \sim \mathcal{N}(T \mu + b, T C T^\top)$로 주어지는 속성을 사용하며, $q(x_t \vert x_0)$는 다음과 같이 완화된다.

\[\begin{equation} q(x_t \vert x_0) = \mathcal{N} (x_t; \sqrt{\vphantom{1} \bar{\alpha}_t} T x_0, (1 - \bar{\alpha}_t) T T^\top) \end{equation}\]

이것으로부터 posterior의 closed form 표현을 도출할 수 있다.

\[\begin{equation} q(x_{t-1} \vert x_t, x_0) = \mathcal{N} (x_{t-1} \vert \tilde{\mu}_t (x_t, x_0), \tilde{\beta}_t T T^\top) \\ \tilde{\mu}_t (x_t, x_0) = \frac{\sqrt{\vphantom{1} \bar{\alpha}_{t-1}} \beta_t}{1 - \bar{\alpha}_t} T x_0 + \frac{\sqrt{\alpha_t} (1 - \bar{\alpha}_{t-1})}{1 - \bar{\alpha}_t} x_t \\ \tilde{\beta}_t = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \end{equation}\]

완화된 Gaussian 밀도

\[\begin{equation} p_\theta (x_{t-1} \vert x_t) = \mathcal{N} (x_{t−1} \vert \mu_\theta (x_t, t), \sigma_t^2 T T^\top) \end{equation}\]

와 유사하게 reverse transition를 정의하면 $\mu_\theta : \mathcal{H} \rightarrow \mathcal{H}$를 parameterize하여 $x_0$를 직접 예측할 수 있다. Loss는 무한 차원으로 확장될 수 있으며 무한 차원에서 잘 정의된다. 그러나 DDPM의 주요 결과는 noise를 예측하기 위해 다시 parameterize하면 훨씬 더 높은 이미지 품질을 얻을 수 있다는 것이다. 이 경우 $\mu_\theta$의 연속적인 특성으로 인해 white noise를 직접 예측하는 것은 실용적이지 못하다. 대신, loss를 다음과 같이 다시 써서 $\xi \sim \mathcal{N} (0, C_I)$에 대해 $T \xi$를 예측하기 위해 $\mu_\theta$를 다시 parameterize한다.

\[\begin{equation} \mathcal{L}_{t-1} = \mathbb{E}_q \bigg[ \frac{1}{2 \sigma_t^2} \bigg\| T^{-1} \bigg( \frac{1}{\sqrt{\alpha}_t} \bigg( x_t (x_0, \xi) - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} T \xi \bigg) - \mu_\theta (x_t, t) \bigg) \bigg\|_{\mathcal{H}}^2 \bigg] \\ \mu_\theta (x_t, t) = \frac{1}{\sqrt{\alpha}_t} \bigg[ x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} f_\theta (x_t, t) \bigg] \end{equation}\]

$x_0$을 직접 예측하면 본질적으로 완화되지 않은 데이터의 추정치를 제공하지만 $T \xi$를 예측할 때 $T x_0$만 샘플링할 수 있지만 Wiener filter를 사용하여 이 프로세스를 취소할 수 있다. 유사한 기술을 사용하여 loss를 계산할 수 있지만 이 경우 $T^{-1}$은 최소값에 영향을 미치지 않으므로 대신

\[\begin{equation} \mathcal{L}_{t-1}^\textrm{simple} = \mathbb{E}_q [ \| f_\theta (x_t, t) - T \xi \|_{\mathcal{H}}^2] \end{equation}\]

을 사용할 수 있다. noise만 완화되는 diffusion process를 정의하는 것도 가능하지만 noise가 데이터보다 낮은 주파수가 되기 때문에 잘 작동하지 않을 가능성이 있다. 또한 DDIM을 이 설정에 직접 적용하여 $T \xi$에서 deterministic한 샘플링 프로세스를 얻을 수 있다.

3. Continuous Time Diffusion

제안된 무한 차원 diffusion process의 특성을 검토하기 위해 잘 연구된 무한 차원 SDE(확률 미분 방정식)를 고려한다. 특히, Banach space $\mathcal{X}$에서 값을 취하는 SDE는 분리 가능한 Hilbert space $\mathcal{H}$에 연속적으로 포함된다.

\[\begin{equation} dx = F(x, t)dt + \sqrt{2} d w(t) \end{equation}\]

여기서 drift $F$는 $\mathcal{H}$의 값을 취하고 프로세스 $x$는 $\mathcal{X}$의 값을 가지며 $w$는 $\mathcal{H}$에 대한 cylindrical Wiener process이다. 무한 차원 SDE는 계수가 일부 규칙성 조건을 만족하는 한 고유한 강력한 해를 갖는다. 특히 모든 $x, y \in C([0, T], \mathcal{H}), 0 \le t \le T$에 대해 Lipschitz 조건이 충족되면, 다음과 같은 $h > 0$가 존재한다.

\[\begin{equation} \| F(x, t) - F(y, t) \|_{\mathcal{H}} \le h \sup_{0 \le s \le T} \| x(s) - y(s) \| \end{equation}\]

유한 차원의 경우와 유사하게 reverse diffusion은 시간을 거꾸로 실행하는 또 다른 SDE로 설명할 수 있다.

\[\begin{equation} dx = [F(x, t) - 2D \log p_t (x)] dt + \sqrt{2} d \bar{w} (t) \end{equation}\]

그러나 유한 차원의 경우와 달리 이것은 특정 조건에서만 성립한다. 상호 작용이 너무 강하면 SDE의 종단 위치에 너무 많은 정보가 포함되어 임의의 좌표의 궤적을 재구성할 수 있다. Drift 항의 에너지가 유한하도록 함으로써 이를 방지할 수 있다.

\[\begin{equation} \mathbb{E} \bigg[ \int_0^T F^i (x, t)^2 dt \bigg] < \infty, \quad \forall i \in D \end{equation}\]

Diffusion space를 완화하는 것은 SDE를 preconditioning하는 것과 유사하다. 이러한 SDE를 discretise하여 얻은 MCMC 접근 방식은 mesh refinement에서의 강력한 샘플링 속도와 같은 강력한 속성을 생성한다.

Parameterising the Diffusion Process

Hilbert space에서 score function을 모델링하기 위해 학습 가능한 함수 클래스가 무한 해상도 데이터에 대한 학습을 허용하기 위해 충족해야 하는 특정 속성이 있다.

1. 임의의 좌표에 위치한 입력 포인트로 취할 수 있다.
2. 정규 격자에서 샘플링된 학습된 것과 다른 수의 입력 포인트로 일반화된다.
3. 글로벌한 정보와 로컬한 정보 모두를 캡처할 수 있다.
4. 매우 많은 수의 입력 포인트로 확장된다. 즉, 런타임 및 메모리 측면에서 효율적이다.

최근의 diffusion model은 글로벌한 정보와 로컬한 정보를 모두 효율적으로 캡처할 수 있도록 해상도 간에 skip connection이 있는 convolutional 인코더와 디코더로 구성된 U-Net을 자주 사용한다. 불행하게도 U-Net은 고정 격자에서 작동하므로 적합하지 않다. 그러나 원하는 속성을 만족하는 아키텍처를 구축하기 위해 영감을 얻을 수 있다.

1. Neural Operators

Neural operator는 단일 step에서 PDE(편미분 방정식) 파라미터를 해에 직접 매핑하는 방법을 학습하여 PDE를 효율적으로 풀도록 설계된 프레임워크다. 그러나 보다 일반적으로 무한 차원 diffusion model을 parameterize하는 데 적합하도록 두 개의 무한 차원 함수 space 사이의 map을 학습할 수 있다.

$\mathcal{X}$와 $\mathcal{S}$를 noise가 제거된 데이터의 space를 각각 나타내는 분리 가능한 Banach space라고 하자. Neural operator는 map $\mathcal{F}_\theta : \mathcal{X} \rightarrow \mathcal{S}$이다. $x \in \mathcal{X}$와 $s \in \mathcal{s}$는 둘 다 함수이므로 pointwise 평가에만 액세스할 수 있다. $\mathbf{c} \in \binom{D}{m}$을 도메인의 $m$-point discretisation이라고 하고 관측값 $x(\mathbf{c}) \in \mathbb{R}^{m \times d}$이 있다고 가정하자. Discretisation에 불변이기 위해 neural operators는 임의의 $c \in D$, 잠재적으로 $c \notin \mathbf{c}$에서 평가될 수 있으므로 서로 다른 discretisation 사이에서 해를 전달할 수 있다. 즉, 속성 1과 2를 만족한다. 각 연산자 레이어는 로컬하지 않은 적분 정보를 공간적으로 집계하는 커널 연산자 $\mathcal{K} (x;\phi)$를 사용하여 구축된다.

\[\begin{equation} (\mathcal{K} (x; \phi) v_l) (c) = \int_D \kappa (c, b, x(c), x(b); \phi) v_l (b) db, \quad \forall c \in D \end{equation}\]

신경망은 비선형 activation 함수를 사용하여 선형 연산자 레이어를 쌓아 기존 방법과 유사한 방식으로 구축할 수 있다.

\[\begin{equation} v_0 \mapsto v_1 \mapsto \cdots \mapsto v_L \end{equation}\]

여기서 $v_l \mapsto v_{l+1}$은 다음과 같이 정의된다.

\[\begin{equation} v_{l+1} (c) = \sigma (W v_l (c) + (\mathcal{K} (x; \phi) v_l) (c)), \quad \forall c \in D \end{equation}\]

여기서 $W : \mathbb{R}^d \rightarrow \mathbb{R}^d$는 pointwise 선형 변환이고, $\sigma : \mathbb{R} \rightarrow \mathbb{R}$는 비선형 activation 함수이다.

2. Architecture

Galerkin attention (softmax가 없는 선형 attention 연산자)이나 MLP-Mixers와 같이 필요한 모든 속성을 만족하는 neural operator가 존재하지만 역전파를 위한 activation 캐싱과 관련된 높은 메모리 비용으로 인해 적은 수의 좌표를 넘어서는 확장은 여전히 어렵다. 대신 네트워크를 통해 서로 다른 지점에서 로컬 및 글로벌로 정보를 집계하는 U-Net에서 영감을 받은 멀티스케일 아키텍처를 설계한다.

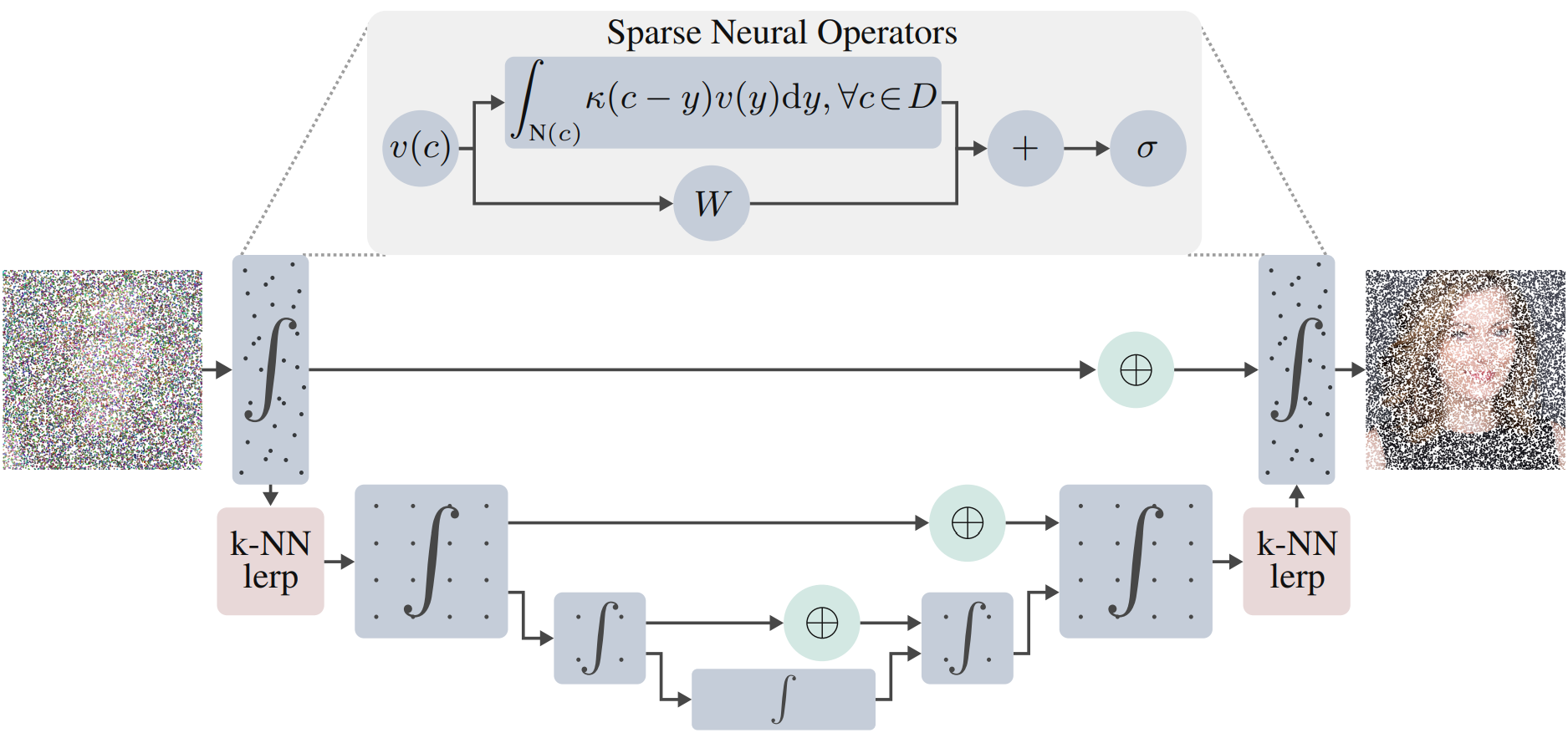
연속적인 세팅에서는 다운샘플링에 대한 두 가지 주요 접근 방식이 있다.

1. 좌표의 부분집합 선택
2. 규칙적인 간격의 격자에서 포인트 interpolation

저자들은 첫번째 접근 방식을 반복적으로 적용하여 포인트가 매우 적은 불균일한 간격의 격자에서 적분 연산자를 근사화하는 것이 높은 분산으로 인해 잘 수행되거나 일반화되지 않는다는 것을 발견했다. 반면에 정규 격자로 작업하면 일부 sparsity 속성이 제거되지만 분산 문제는 훨씬 낮다. 따라서 데이터에 sparse 연산자를 적용한 하이브리드 접근 방식을 사용하여 고정 격자에서 interpolate하고 격자 기반 아키텍처를 적용한다. 고정 격자의 차원이 충분히 높은 경우 이 조합으로 충분하다. FNO 아키텍처를 사용할 수 있지만 해상도 변경에 사용되는 sparse 연산자를 사용하여 dense convolution으로 더 나은 결과를 얻었다고 한다.

Sparse 레벨에서 convolution 연산자를 사용하여 Galerkin attention보다 더 성능이 우수하며 멀티스케일 아키텍처로 인해 글로벌한 컨텍스트가 더 이상 필요하지 않다. 이 경우 연산자는 각 좌표의 로컬 neighborhood $N(c)$로 제한된 translation 불변 커널을 사용하여 정의된다.

\[\begin{equation} x(c) = \int_{N(c)} \kappa (c-y) v(y) dy, \quad \forall c \in D \end{equation}\]

저자들은 큰 커널(특히 지속적으로 parameterize된 커널의 경우)에 대한 더 큰 파라미터 효율성으로 인해 $\kappa$를 depthwise kernel로 제한하고 더 적은 샘플링 좌표로 학습할 때 더 일반화할 수 있음을 발견했다. Sparsity 비율은 일반 convolution과 depthwise convolution에서 동일하지만 일반 커널에는 실질적으로 더 많은 값이 있기 때문에 값 사이에 더 많은 공간적 상관 관계가 있다.

매우 많은 수의 샘플링된 좌표가 사용되는 경우 완전히 연속적인 connection은 메모리 사용 및 실행 시간 측면에서 매우 비실용적이다. 그러나 실제로는 이미지를 가져와 개별 격자에 저장한다. 이와 같이 이미지를 고차원이지만 이산적인 개체로 취급함으로써 효율적인 sparse convolution 라이브러리를 활용하여 메모리 사용과 실행 시간을 훨씬 더 합리적으로 만들 수 있다. 저자들은 depthwise connection을 허용하도록 수정된 TorchSparse를 사용하였다.

낮은 불일치 좌표 시퀀스를 사용하여 더 나은 수렴 속도로 적분을 근사화할 수 있다. 그러나 저자들은 균일하게 샘플링된 포인트가 더 효과적이라는 것을 발견했다. 이는 축소된 구조로 인해 포인트가 서로 가깝게 샘플링되어 고주파 디테일을 더 쉽게 캡처할 수 있기 때문일 수 있다.

Experiments

Sample Quality

다음은 ∞-Diff 모델의 샘플들이다.

다음은 입력을 무한 차원 데이터로 취급하는 접근 방식들과 비교한 표이다.

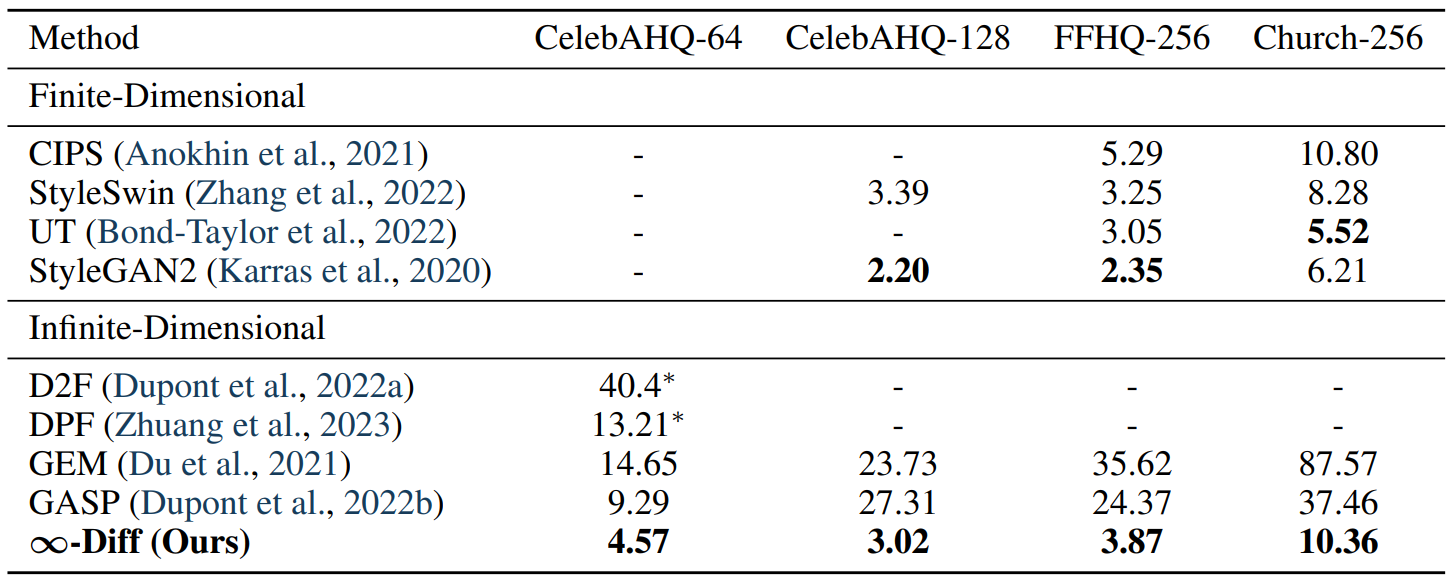
다음은 무한 차원 접근 방식들과 정성적으로 비교한 것이다.

Discretisation Invariance

다음은 ∞-Diff의 discretisation invariance 속성을 설명하기 위한 그림이다. 왼쪽부터 64$\times$64에서 1024$\times$1024이다.

다음은 다양한 샘플링 step과 해상도에 대한 이미지 품질을 나타낸 그래프이다.

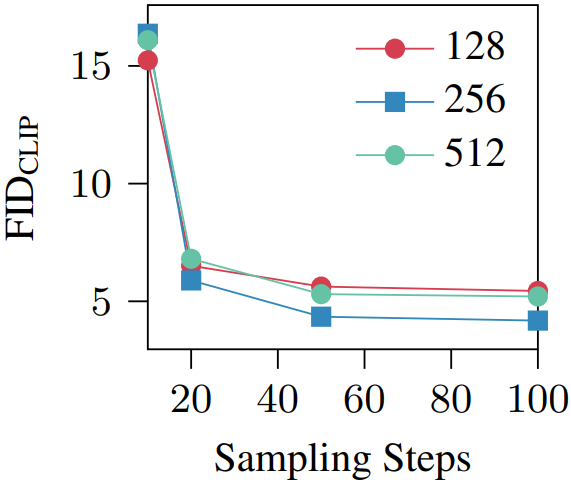
Coordinate Sparsity

다음은 FFHQ 128에서 좌표의 sparsity의 영향을 나타낸 표이다.

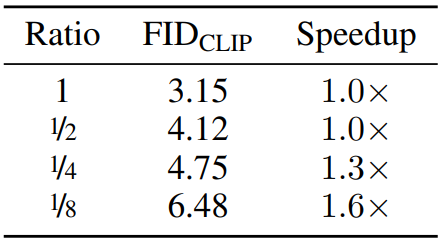
더 적은 좌표를 사용하면 성능이 감소하지만 효과가 그리 크지 않다. 또한 더 적은 좌표를 사용하면 샘플링 속도를 가속할 수 있으며 메모리를 절약할 수 있다.

Architecture Analysis

다음은 다양한 아키텍처 선택에 대한 ablation study 결과이다.

Super-resolution

Discretisation invariance 속성은 super-resolution을 자연스럽게 적용한다. 인코더를 통해 저해상도 이미지를 전달한 다음 고해상도에서 샘플링하는 간단한 방법으로 이를 평가할 수 있다.

다음은 ∞-Diff를 활용한 super-resolution의 예시이다.

분명하게 디테일이 더 추가됨을 확인할 수 있다. 이 접근 방식의 단점은 인코딩 프로세스에서 정보가 손실된다는 것이다. 그러나 DDIM 인코딩을 통합하여 잠재적으로 개선할 수 있다.

Inpainting

Reconstruction guidance를 사용하여 mollified diffusion으로 인페인팅이 가능하다.

\[\begin{equation} x_{t-1} \leftarrow x_{t-1} - \lambda \nabla_{x_t} \| m \odot (\tilde{\mu}_0 (x_t, t) - T \bar{x}) \|_2^2 \end{equation}\]

$m$은 inpainting mask이다. 인페인팅 결과는 아래와 같다.

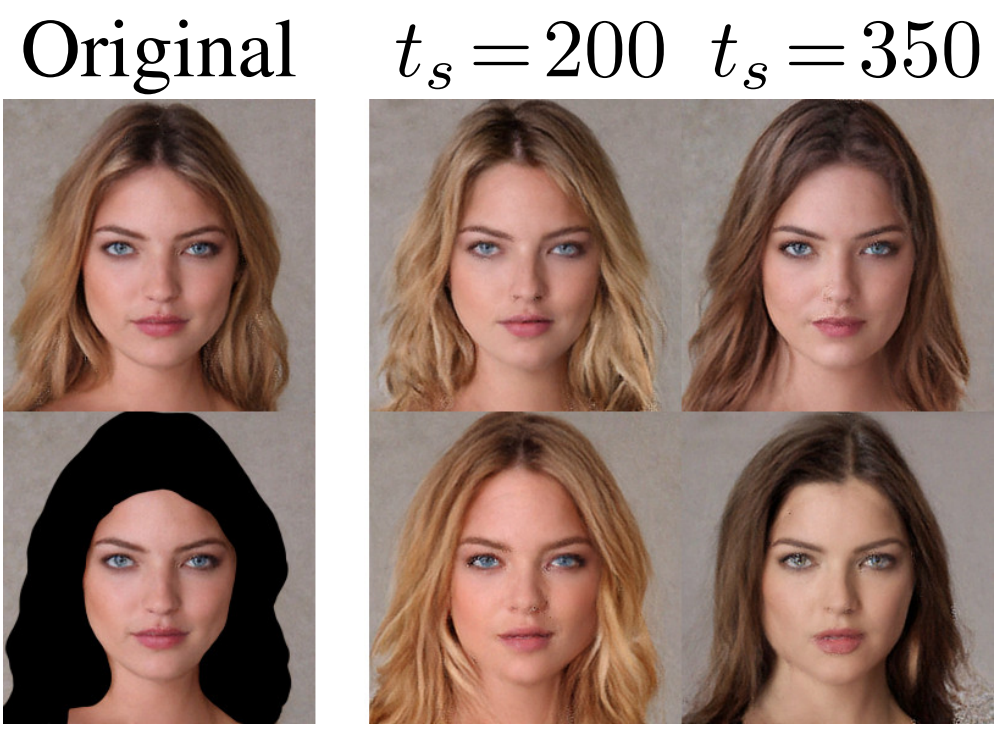
Diffusion autoencoder 프레임워크는 인페인팅 시 reverse process가 선택한 timestep $t_s$의 인코딩에 적용될 수 있으므로 인페인팅할 때 추가적인 제어 레벨을 제공하여 인페인팅 영역이 원본 이미지와 얼마나 다른지 제어할 수 있다.