[논문리뷰] Image-GS: Content-Adaptive Image Representation via 2D Gaussians

SIGGRAPH 2025. [Paper] [Github]
Yunxiang Zhang, Bingxuan Li, Alexandr Kuznetsov, Akshay Jindal, Stavros Diolatzis, Kenneth Chen, Anton Sochenov, Anton Kaplanyan, Qi Sun
New York University | AMD | Intel Corporation
2 Jul 2024

Introduction

신경망 기반 이미지 표현은 시각 데이터 인코딩을 위한 유망한 대안으로 떠오르고 있다. 학습 기반 파이프라인에 통합되면 기존 포맷에 비해 뛰어난 시각적 충실도와 메모리 효율성을 제공한다. 그러나 기존 방식은 콘텐츠 적응성이 부족한 고정된 데이터 구조나 계산 집약적인 신경망 모델에 의존하는 경우가 많아 확장성이 떨어지고 디코딩 속도가 느리다. 이러한 단점은 빠른 랜덤 액세스와 기기 성능에 따른 동적 품질 조정이 중요한 실시간 그래픽 환경에서의 사용을 저해한다.

본 논문은 이러한 간극을 메우기 위해 각각 평균, 공분산, 색상으로 정의된 2D Gaussian들을 기반으로 하는 명시적 이미지 표현인 Image-GS를 소개한다. Image-GS는 타겟 이미지가 주어지면, image gradient 크기에 따라 Gaussian 그룹을 적응적으로 초기화하고, 더 높은 주파수 영역에 더 많은 Gaussian을 할당한다. 파라미터들은 이미지를 재구성하기 위해 미분 가능한 커스텀 렌더러를 사용하여 최적화된다. 지속적인 아티팩트가 있는 영역에는 추가적인 Gaussian을 점진적으로 추가하여 재구성 품질을 더욱 개선한다. Image-GS의 적응형 설계는 이미지에서 불균일하게 분포된 feature와 semantic 구조를 포착하여 제한된 메모리 예산 내에서 미세한 디테일을 더 잘 보존할 수 있도록 한다. 실시간 사용을 용이하게 하기 위해, Image-GS의 전체 렌더링 파이프라인은 최적화된 CUDA 커널로 구현되어 계산 병렬성을 극대화하였다.

Image-GS는 시각적 충실도와 메모리/연산 비용 간의 유리한 균형을 보여주며, 특히 균일하지 않게 분포된 feature를 가진 그래픽 에셋과 낮은 비트레이트 환경에서 효과적이다. 또한, Image-GS는 빠른 병렬 디코딩과 하드웨어 친화적인 랜덤 액세스, 그리고 매끄러운 LOD (level-of-detail) 계층 구조를 통한 유연한 품질 관리를 지원한다. 저자들은 Image-GS의 다재다능함을 보여주기 위해, semantic-aware 압축과 이미지 복원이라는 두 가지 응용 분야에 Image-GS를 적용하였다.

Method

1. Representing Images as 2D Gaussians

3D Gaussian Splatting (3DGS)의 Gaussian primitive와 유사하게 2D Gaussian의 geometry는 평균 벡터 $\boldsymbol{\mu} \in \mathbb{R}^2$와 공분산 행렬 $\boldsymbol{\Sigma} \in \mathbb{R}^{2 \times 2}$로 정의되며, 임의의 픽셀 위치 $\textbf{x} \in \mathbb{R}^2$에서 평가된 값은 다음과 같이 표현할 수 있다.

\[\begin{equation} G(\textbf{x}) = \exp \left( -\frac{1}{2} (\textbf{x} - \boldsymbol{\mu})^\top \boldsymbol{\Sigma}^{-1} (\textbf{x} - \boldsymbol{\mu}) \right) \end{equation}\]

수치 최적화 중에 $\boldsymbol{\Sigma}$가 positive semi-definite로 유지되도록 하기 위해 rotation matrix $\textbf{R} \in \mathbb{R}^{2 \times 2}$와 scaling matrix $\textbf{S} \in \mathbb{R}^{2 \times 2}$로 구성된다.

\[\begin{equation} \boldsymbol{\Sigma} = \textbf{R} \textbf{S} \textbf{S}^\top \textbf{R}^\top \end{equation}\]

구체적으로, 각 2D Gaussian에 대해 회전 각도 $\theta \in [0, \pi]$와 scaling 벡터 $\textbf{s} \in \mathbb{R}_{+}^2$를 설정하고 유지한다. 이러한 속성들은 stochastic gradient descent를 통해 업데이트되고 학습 과정에서 유효 범위에 맞춰 clipping된다. $\textbf{R}$과 $\textbf{S}$는 학습 및 inference 과정에서 $\theta$, $\textbf{s}$를 통해 실시간으로 생성된다.

Spherical harmonics를 사용하여 시점에 따른 외형을 모델링하는 3DGS와 달리, 이미지는 본질적으로 3D 장면의 하나의 시점을 보여주므로 각 2D Gaussian을 벡터 $\textbf{c} \in \mathbb{R}^n$과 연결하여 색상을 저장하기만 하면 된다. 특히, 가변적인 색상 차원 $n$을 사용함으로써 Image-GS는 grayscale, RGB, CMYK 이미지뿐만 아니라 다중 채널 텍스처 스택을 포함한 다양한 이미지 형식을 유연하게 지원할 수 있다.

3DGS는 알파 블렌딩을 위해 불투명도 속성을 사용하지만, 2D Gaussian의 색상 정보는 상대적인 순서에 관계없이 효과적으로 집계될 수 있다. 따라서 2D Gaussian에는 불투명도 속성이 없다.

위의 구성 요소를 결합하면 Image-GS의 각 2D Gaussian primitive는 $5+n$개의 학습 가능한 파라미터로 구성된다.

\[\begin{equation} \textbf{p}_i := \textbf{p}_i (\boldsymbol{\mu}_i, \theta_i, \textbf{s}_i, \textbf{c}_i) \in \mathbb{R}^{5+n}, \quad 1 \le i \le N_g \end{equation}\]

2. Rendering 2D Gaussians into Images

3DGS는 occlusion을 처리하고 멀티뷰 일관성을 유지하기 위해 불투명도와 깊이 정렬이 필요하지만, 2D의 경우에는 이러한 요구 사항이 불필요하다. 특히, 색상이 있는 Gaussian blob 집합을 보여주는 이미지는 가중치가 적용된 색상을 합산하여 렌더링할 수 있으며, 결과 이미지는 Gaussian 적용 순서에 관계없이 동일하다.

따라서, 2D Gaussian을 점들의 순서 없는 집합으로 처리하고 색상 기여도를 누적하여 이미지 픽셀 \(\textbf{c}_r (\textbf{x}) \in \mathbb{R}^n\)을 렌더링하여 알파 블렌딩 방정식을 단순화한다.

\[\begin{equation} \textbf{c}_r (\textbf{x}) = \sum_{i=1}^{N_g} G_i (\textbf{x}) \cdot \textbf{c}_i \end{equation}\]

그러나 이러한 단순한 공식은 픽셀을 렌더링하는 데 모든 Gaussian을 사용하므로 렌더링 및 학습 속도가 크게 저하된다. 또한, 이런 dense한 픽셀-Gaussian 상관관계는 GPU 애플리케이션에서 빠른 픽셀 랜덤 엑세스에 필수적인 데이터 지역성(locality)을 크게 저해한다.

이 문제를 해결하기 위해 타일 기반 렌더링 방식을 취하고 픽셀에 기여할 수 있는 Gaussian의 수를 제한한다. 먼저, 이미지의 공간적 지원을 크기가 $H_t \times W_t$인 겹치지 않는 타일로 세분화한다. 그런 다음, 각 2D Gaussian의 3-sigma 범위를 둘러싸는 가장 작은 원을 계산하고 모든 쌍에서 타일-원 교차점을 확인하여 타일-Gaussian 대응 관계를 설정한다. 둘러싸는 원이 타일 $T_j$와 교차하는 Gaussian 집합을 \(\mathcal{S}_j\)라 하면, 각 픽셀 $\textbf{x} \in 𝑇_𝑗$에 대해, $\textbf{x}$에서 계산된 값을 기준으로 \(\mathcal{S}_j\)의 모든 Gaussian의 순위를 매기고, 상위 $K$개만 유지한다. 마지막으로, $K$개의 Gaussian의 값을 normalize하고, 가중치 색상을 합산하여 \(\textbf{c}_r (\textbf{x})\)를 구한다.

\[\begin{equation} \textbf{c}_r (\textbf{x}) = \frac{1}{\sum_{i \in \mathcal{S}_j^K (\textbf{x})} G_i (\textbf{x})} \sum_{i \in \mathcal{S}_j^K (\textbf{x})} G_i (\textbf{x}) \cdot \textbf{c}_i, \quad 1 \le j \le N_t \end{equation}\]

3. Content-Adaptive Initialization and Optimization

미분 가능 렌더러를 기반으로, stochastic gradient descent를 통해 Gaussian 속성 \(\textbf{p}_i\)를 최적화하여 임의의 타겟 이미지를 재구성한다. 현재 신경망 기반 이미지 표현에 사용되는 신경망 모델과 달리, Image-GS는 물리적 의미를 가진 명시적 feature들만으로 구성되므로, 더 빠르고 고품질의 수렴을 위해 task별 초기화를 활용하는 것이 유리하다. 특히, 이상적인 초기화는 이미지 콘텐츠에 따라 결정되어야 하며, Gaussian의 공간적 분포는 고주파 이미지 feature의 공간적 분포와 일치해야 한다.

이를 위해, 저자들은 콘텐츠 적응형 위치 초기화 전략을 제안하였다. 구체적으로, 각 Gaussian의 위치 샘플링 동안 (픽셀 중심만 샘플링), 픽셀 $\textbf{x}$가 샘플링될 확률은 해당 픽셀의 image gradient의 상대적인 크기와 모든 픽셀 위치에 걸쳐 공유되는 상수의 가중 합이다. 특히, 전자는 이미지 콘텐츠 적응성을 강조하는 반면, 후자는 전체 이미지 영역에 대한 적절한 커버리지를 보장한다.

\[\begin{equation} \mathbb{P}_\textrm{init} (\textbf{x}) = \frac{(1 - \lambda_\textrm{init}) \cdot \| \nabla I(\textbf{x}) \|_2}{\sum_{h=1}^H \sum_{w=1}^W \| \nabla I(\textbf{x}_{h, w}) \|_2} + \frac{\lambda_\textrm{init}}{H \cdot W}, \quad \lambda_\textrm{init} \in [0, 1] \end{equation}\]

또한 모든 Gaussian에는 초기화된 위치 \(\textbf{c}_t (\textbf{x})\)에서의 타겟 픽셀 색상이 지정된다.

각 최적화 단계에서 Gaussian 집합은 이미지로 렌더링되며, 이를 통해 타겟 이미지에 대한 L1 loss와 SSIM loss의 조합을 계산한다. 전체 파이프라인은 미분 가능하므로, 모든 Gaussian 속성은 stochastic gradient descent를 통해 업데이트되어 재구성을 향상시킬 수 있다.

top-K ranking 연산은 미분 불가능하지만, gradient는 연산 자체를 통과하지 않고 $K$개의 Gaussian을 통과한다. 경험적으로, top-K normalization은 데이터 지역성을 향상시킬 뿐만 아니라 재구성 품질도 향상시키며, 최적화 과정에서 일종의 정규화 역할을 한다.

처음에 도입된 Gaussian 외에도, 높은 재구성 오차를 보이는 이미지 영역에 새로운 Gaussian을 점진적으로 추가한다. 이는 오차 크기에 따라 픽셀을 샘플링하고 샘플링된 위치에 새로운 Gaussian을 초기화하는 방식으로 이루어진다.

\[\begin{equation} \mathbb{P}_\textrm{add} (\textbf{x}) = \frac{\vert \textbf{c}_r (\textbf{x}) - \textbf{c}_t (\textbf{x}) \vert}{\sum_{h=1}^H \sum_{w=1}^W \vert \textbf{c}_r (\textbf{x}_{h,w}) - \textbf{c}_t (\textbf{x}_{h,w}) \vert} \end{equation}\]

Evaluation

1. Ablation Study

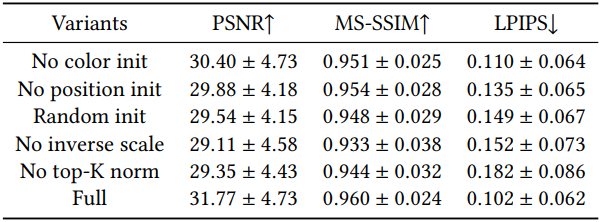
다음은 ablation study 결과이다.

2. Image Compression Performance

다음은 다양한 이미지 표현 방식들과 비교한 결과이다.

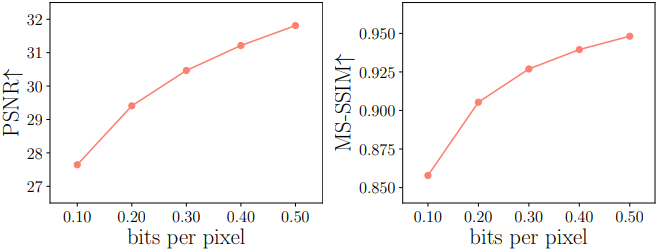
다음은 Image-GS의 rate-distortion trade-off를 분석한 결과이다.

3. System Performance

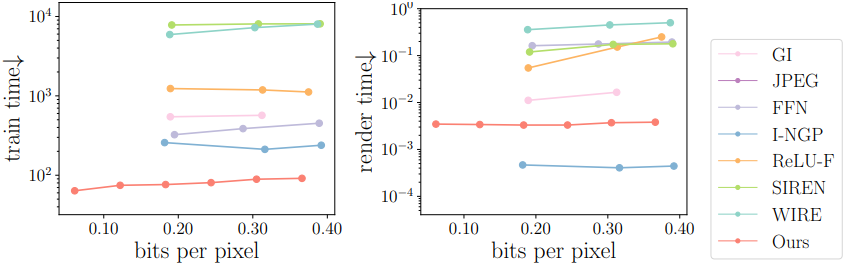
다음은 학습 시간과 렌더링 시간을 비교한 결과이다.

4. Texture Compression Performance

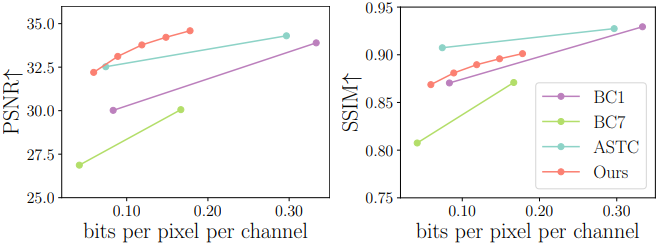
다음은 텍스처 압축 성능을 비교한 결과이다.층

5. Applications

다음은 0.2 bpp로 압축하였을 때의 VQA 결과이다. (BLIP-2)

다음은 노이즈를 추가한 이미지를 Image-GS로 압축하여 이미지 복원을 동시에 수행한 결과이다. 압축 시 픽셀 수준의 노이즈보다 이미지 콘텐츠에 더 많은 비트가 할당된다.