[논문리뷰] Implicit Gaussian Splatting with Efficient Multi-Level Tri-Plane Representation

arXiv 2024. [Paper]
Minye Wu, Tinne Tuytelaars
KU Leuven
19 Aug 2024

Introduction

3DGS의 컴팩트한 표현에 대한 최근 방법은 주로 세 가지로 나뉜다.

1. Gaussian의 수를 줄이는 데 중점을 둔 방법. 표현 능력에 어느 정도 영향을 미쳐 렌더링 품질이 저하된다.
2. 효율적인 장면 표현을 위해 앵커 기반 표현 (ex. Scaffold-GS)이나 generalized exponential function (ex. GES)을 사용한 방법. 저장 공간을 어느 정도 줄이지만 여전히 ​​상당하다.
3. 3DGS에 vector quantization을 채택한 방법. Gaussian 속성에 대한 codebook을 구성하고 run-length coding과 DEFLATE 압축 알고리즘을 사용하여 코드북을 더욱 압축한다. 3DGS의 볼륨을 줄여서 필연적으로 렌더링 품질이 저하된다.

핵심 문제는 Gaussian들이 위치와 속성에서 독립적이고 불규칙하다는 것이다. 학습된 3DGS의 로컬한 영역에서 다양한 모양과 방향을 가진 3D Gaussian을 관찰할 수 있다. 이로 인해 Gaussian 간의 공간적 상관 관계가 감소하고 데이터 엔트로피가 증가하여 압축이 어려워지고 대부분 알고리즘이 품질과 저장 크기 간의 적절한 균형을 찾는 데 어려움을 겪는다. 이 문제를 해결하는 한 가지 접근 방식은 Gaussian 간의 관계를 설정하고 최적화 중에 제약 조건을 부과하는 것이다.

Scaffold-GS에서는 앵커 기반 표현을 기반으로 Gaussian 사이의 관계를 설정하였다. Scaffold-GS는 최적화 중에 앵커 feature 임베딩 간의 연결을 암시적으로 설정하고 우수한 성능을 보였다. 이러한 암시적 모델링과 대조적으로, 본 논문의 방법은 Gaussian의 공간적 상관 관계를 명시적으로 모델링하고 공간 도메인에서 후속 정규화를 가능하게 한다.

본 논문은 Gaussian을 명시적인 포인트 클라우드와 암시적인 속성 feature로 분리하는 새로운 하이브리드 표현을 제시하였다. 속성 feature는 residual 기반 렌더링 파이프라인과 통합된 multi-resolution multi-level tri-plane 아키텍처 내에서 인코딩된다. 이 디자인은 discrete한 Gaussian을 연속적인 공간 도메인으로 옮겨 Gaussian들 사이의 공간적 상관 관계를 향상시킨다. 이 공간적 feature 도메인 내에서 각 Gaussian의 모양, 불투명도, 색상이 암시적으로 인코딩되어 장면 공간의 매우 컴팩트하고 효율적으로 인수분해된다.

저자들은 이 표현을 기반으로 포인트 클라우드와 multi-level tri-plane의 공동 최적화를 가능하게 하는 레벨 기반 점진적 학습 방식을 제안하였다. 이 프레임워크에서 가장 컴팩트한 feature를 갖춘 하위 레벨에서 coarse한 Gaussian 속성을 생성한다. 그런 다음 상위 레벨의 tri-plane이 residual을 예측하는 데 사용되어 하위 레벨 출력에 존재하는 오차를 효과적으로 보상한다.

추가로, tri-plane의 공간적 정규화를 적용하여 공간의 로컬 영역 내에서 Gaussian 속성의 일관성을 최적화하였다. 포인트 클라우드 최적화의 안정성을 개선하기 위해 초기 학습 단계에서 속성의 혼합 표현을 활용하는 부트스트래핑 방식을 도입하였다. 또한, splatting 기반 표현의 특성을 활용하여 포인트 클라우드 정렬 및 feature quantization 기술을 사용하여 매우 컴팩트한 저장 공간을 달성하는 맞춤형 압축 파이프라인을 도입하였다.

Methods

1. Multi-Level Tri-Plane

본 논문은 공간적 상관 관계를 강화하는 동시에 컴팩트한 표현을 달성하는 새로운 multi-level tri-plane 아키텍처를 도입하였다. 3DGS에서 tri-plane을 적용하는 데는 몇 가지 문제가 있다.

1. 단일 레벨 tri-plane은 용량이 제한적이다. Gaussian 속성 예측의 정확도를 개선하려면 feature 평면의 해상도를 높여야 하지만, 이는 컴팩트성을 저하시킨다.
2. Feature는 그리드에서 interpolation을 통해 얻어지므로 본질적으로 이웃 vertex들의 정보를 포함하여 공간적 연결을 설정한다. Receptive field는 그리드 크기에 따라 달라진다. 해상도를 낮추면 feature의 관심 영역이 확장되어 공간적 상관 관계가 강화되지만, 이러한 trade-off는 정확도에 부정적인 영향을 미친다.

좋은 정확도와 공간적 상관관계를 얻기 위해, Feature Pyramid Network (FPN)에서 영감을 얻어, multi-level tri-plane을 사용한다. 이 평면은 3개의 레벨로 구성되며, 각 레벨은 서로 다른 해상도의 tri-plane과 동일한 크기의 개별 MLP 디코더로 구성된다. 하위 레벨은 해상도가 낮고, 해상도는 상위 레벨의 절반이다. 첫 번째 레벨은 coarse한 Gaussian 속성을 디코딩하고, 다른 레벨은 그 위에 있는 속성의 residual을 디코딩하여 오차를 보상한다. 쿼리된 3D 포인트 $\mathbf{p}$가 주어지면, Gaussian 속성은 다음과 같다.

\[\begin{equation} \alpha, \mathbf{s}, \mathbf{q}, \mathbf{h} = \sum_{l=1}^3 \Phi^l (\mathbf{f}_\mathbf{p}^l) \end{equation}\]

• $\alpha$: 불투명도
• $\mathbf{s}$: scaling matrix의 대각 성분
• $\mathbf{q}$: rotation matrix의 quaternion 표현
• $\mathbf{h}$: SH 계수
• $\mathbf{f}_\mathbf{p}^l$: $\mathbf{p}$에서의 $l$번째 레벨 feature,
• $\Phi^l$: $l$번째 레벨의 MLP

2. Level-Based Progressive Training

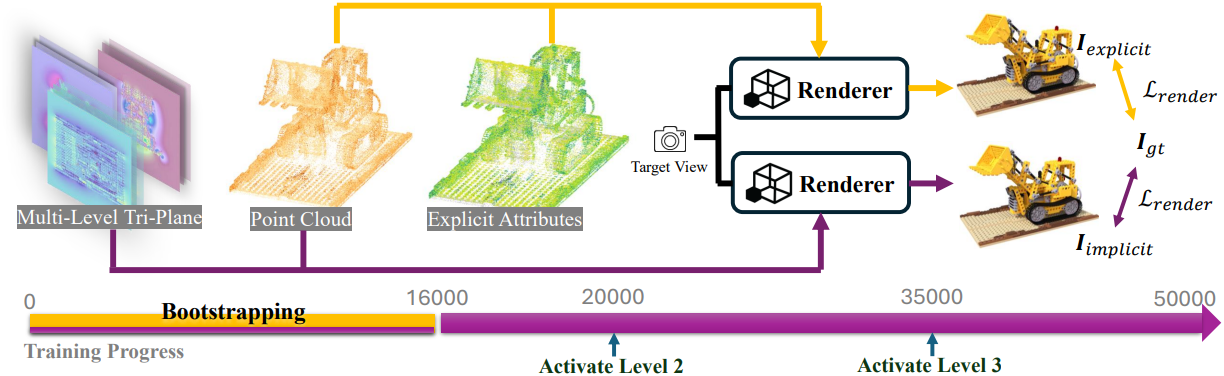
IGS는 컴팩트한 장면 표현을 학습하고 고품질 렌더링을 달성하는 것을 목표로 한다. 이를 위해 여러 부분으로 구성된 맞춤형 학습 계획을 사용한다.

부트스트래핑

IGS는 end-to-end의 미분 가능한 렌더링 파이프라인을 사용하는데, 여기서 포인트 클라우드와 multi-level tri-plane은 공동으로 최적화된다. 암시적인 파라미터와 명시적인 변수의 최적화 속도는 다르다. 암시적인 feature 평면과 MLP 파라미터는 정확한 수렴을 달성하기 위해 더 많은 iteration이 필요하다. 또한 암시적 파라미터의 부정확성은 명시적인 포인트 클라우드의 최적화에 부정적인 영향을 미칠 수 있다. 이는 최종 결과에 도달하는 데 필요한 iteration을 늘릴 뿐만 아니라 공간적 상관 관계를 간과하여 포인트 클라우드에서 underfitting을 초래할 수 있다.

따라서 처음 $t_b$ iteration 동안 3DGS와 마찬가지로 명시적인 Gaussian 속성을 최적화한다. 동시에 포인트 클라우드와 multi-level tri-plane을 사용하여 이미지를 렌더링한다. 두 렌더링 파이프라인은 동시에 포인트 클라우드에 영향을 미친다. 이렇게 하면 합리적인 포인트 클라우드 초기값을 얻고 IGS 표현에 적용할 수 있다.

점진적 학습

Feature 평면의 낮은 해상도는 압축에 도움이 된다. 따라서 더 낮은 레벨에서 더 많은 장면 정보를 인코딩하는 것이 좋다. 그러나 multi-level tri-plane을 공동으로 학습시키면 더 많은 정보가 고해상도 레벨에 포함되는 경향이 있는데, 이는 용량이 더 크기 때문에 최적화하기가 더 쉽기 때문이다. 따라서 먼저 첫 번째 레벨만 최적화하고 지정된 iteration에서 다른 레벨을 하나씩 점진적으로 활성화시킨다.

첫 번째 레벨은 장면을 표현할 수 있는 능력이 있지만 미세한 디테일을 잃은 coarse한 Gaussian 속성을 학습한다. Coarse한 결과에 따라 다른 레벨은 더 큰 해상도로 고주파 속성을 기록하고 coarse한 속성을 보상한다. 현재 레벨을 학습시키는 동안 이전 레벨도 공동으로 최적화하지만 learning rate는 훨씬 낮다. 이렇게 하면 이전 결과에 비해 크게 변하지 않으면서 결과가 최적에 가까워진다.

공간적 정규화

로컬 영역에서 Gaussian 속성의 불규칙성을 완화하기 위해, 다음과 같이 feature 평면의 공간 도메인에 total variation 정규화를 추가한다.

\[\begin{equation} \mathcal{L}_\textrm{spatial} = \frac{1}{\vert \mathcal{P} \vert} \sum_{\mathbf{F} \in \mathcal{F}} \sum_{\mathbf{p} \in \mathcal{P}} [\| \Delta_u (\mathbf{F}, \mathbf{p}) \|_1 + \| \Delta_v (\mathbf{F}, \mathbf{p}) \|_1] \end{equation}\]

여기서 $\mathcal{F}$는 동일 레벨의 feature 평면이고, $\mathcal{P}$는 각 평면의 픽셀 집합이다. \(\Delta_u (\mathbf{F}, \mathbf{p})\)는 $\mathbf{F}$의 픽셀 $\mathbf{p} := (u, v)$의 feature 벡터와 $(u + 1, v)$의 feature 벡터 간의 차이를 나타내며 \(\Delta_v (\mathbf{F}, \mathbf{p})\)는 $(u, v)$의 feature 벡터와 $(u, v+1)$의 feature 벡터 간의 차이이다.

이 외에도 학습된 feature 평면이 더 sparse해지도록 하기 위해 sparsity loss를 추가한다.

\[\begin{equation} \mathcal{L}_\textrm{sparsity} = \sum_{\mathbf{F} \in \mathcal{F}} \| \mathbf{F} \|_1 \end{equation}\]

이 두 가지 유형의 정규화는 재구성에 도움이 될 뿐만 아니라 압축 성능도 향상시킨다. 더 부드럽고 sparse한 feature 평면은 엔트로피가 더 낮고 압축 크기가 더 작다. 그러나 가장 낮은 레벨의 정규화로 인해 발생하는 저밀도 정보는 모델의 용량을 제한하여 결과적으로 더 높은 레벨의 feature 평면의 엔트로피를 높여 전반적인 압축성이 감소한다. 이 문제를 해결하기 위해 다양한 레벨에서 다른 loss 가중치를 적용한다.

최종 학습 loss $\mathcal{L}$은 다음과 같다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{render} + \sum_{l = 1}^3 \lambda_l [\mathcal{L}_\textrm{sparsity}^l + \lambda_t \mathcal{L}_\textrm{spatial}^l] \end{equation}\]

\(\mathcal{L}_\textrm{render}\)는 3DGS에서 사용한 렌더링 loss이다.

Quantization Adaptation

Feature 평면의 고품질 압축을 위해 최적화 중에 random noise를 도입하여 quantization 프로세스를 더 잘 적응시킨다. 추가된 noise는 $-Q$에서 $Q$ 범위 내의 균일하게 분포된 난수이다. Noise가 추가된 feature 평면은 최적화 중에 이미지를 렌더링하는 데만 사용되며, 정규화 및 테스트 중에 사용되는 feature 평면은 영향을 받지 않는다.

3. Compression

IGS는 컴팩트한 표현을 제공하지만, 포인트 클라우드의 3D 좌표와 결합된 multi-channel feature 평면은 여전히 ​​상당한 저장 공간이 필요하다. 데이터의 중복성이 완전히 활용되지 않기 때문이다. 따라서 저자들은 포인트 클라우드와 feature 평면을 별도로 압축하는 압축 방식을 제안하였다.

Point Cloud Compression

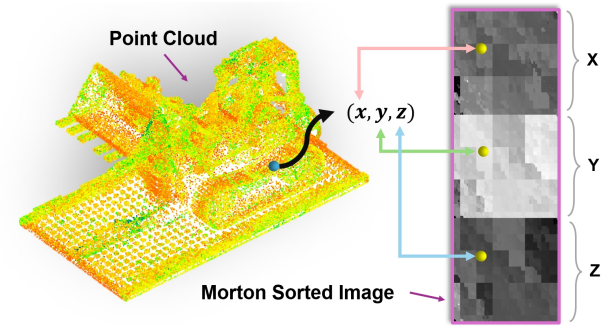
3DGS의 품질은 포인트 위치에 민감하다. 무손실 이미지 압축 알고리즘인 PNG 형식을 활용하여 위 그림에서와 같이 포인트 클라우드의 3D 좌표를 압축시킨다. 구체적으로 bounding box를 사용하여 3D 좌표를 정규화하고 2D 배열로 구성하여 3채널 2D 이미지를 만든다. 그런 다음 각 채널의 2D 배열을 concatenate하여 PNG 알고리즘으로 압축할 수 있는 단일 채널 2D 이미지를 만든다.

압축 알고리즘의 특성에 따르면, 이미지의 로컬 영역이 유사할수록 압축률이 높아진다. 이 특성을 활용하여 Morton sorting을 사용하여 3D 공간에서 2D 공간으로 포인트를 매핑한다. 이는 공간적 로컬성을 효과적으로 보존하므로 3D 공간에서 서로 가까운 포인트는 정렬 후에도 인접하거나 가깝게 유지된다. 최적화된 2D 배열은 압축 시 일반적으로 더 작은 압축 파일을 생성한다.

Feature Plane Compression

포인트 클라우드 압축과 유사하게, feature 평면의 모든 채널에서 2D map을 하나의 채널이 있는 단일 2D 이미지로 결합한다. 표현이 quantization adaptation을 통해 최적화되었고 약간의 오차를 허용할 수 있기 때문에 손실 압축 알고리즘을 사용하여 이 2D 이미지를 압축시킨다. 여기서는 압축을 위해 HEIC를 사용한다.

레벨에 따라 다른 압축 파라미터를 적용한다. 낮은 레벨은 더 높은 품질 파라미터를 갖고 높은 레벨은 더 낮은 품질 파라미터를 갖는다. 결과적으로 가장 중요한 정보를 포함하는 낮은 레벨은 더 높은 정확도로 보존되는 반면, 더 sparse한 정보를 포함하는 높은 레벨은 더 높은 해상도에서도 여전히 크게 압축될 수 있다.

Experiments

• 구현 디테일
  • 가장 큰 feature 평면
  • MLP 디코더
    • 3-layer fully connected network
    • 마지막 레이어를 제외하고 ReLU를 사용
    • scaling 성분은 sigmoid를 적용 후 $[-12, -2]$로 스케일링, 계산 시 지수로 사용
  • bounding box
    • unbounded scene: 모든 카메라를 포함하는 가장 작은 bounding box를 사용
    • single-object scene: 원래 3DGS로 2,000 iteration 학습하여 coarse 포인트 클라우드의 bounding box를 얻음
  • 학습 iteration: 50,000
    • 부트스트래핑: 처음 16,000
    • 레벨 2 활성화: 20,000
    • 레벨 3 활성화: 35,000
  • 학습 시 view frustum 밖의 포인트는 제외하고 MLP에 입력

1. Comparison

다음은 unbounded scene에 대한 성능을 비교한 표이다.

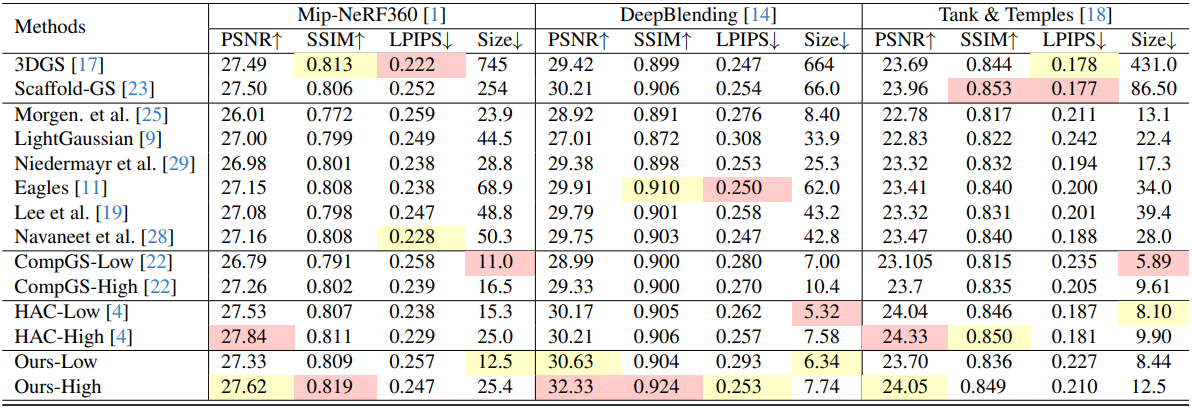
다음은 single-object scene에 대한 성능을 비교한 표이다.

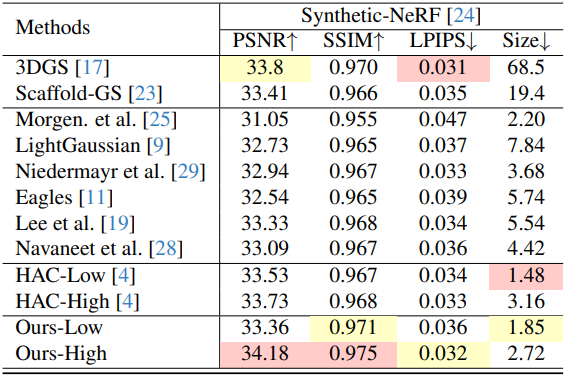
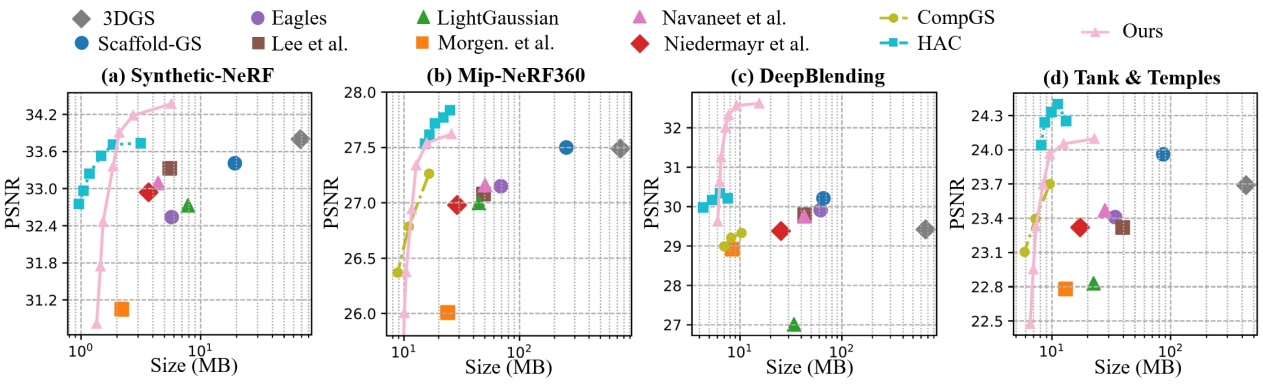
다음은 여러 데이터셋에서 Rate-Distortion curve를 비교한 그래프이다.

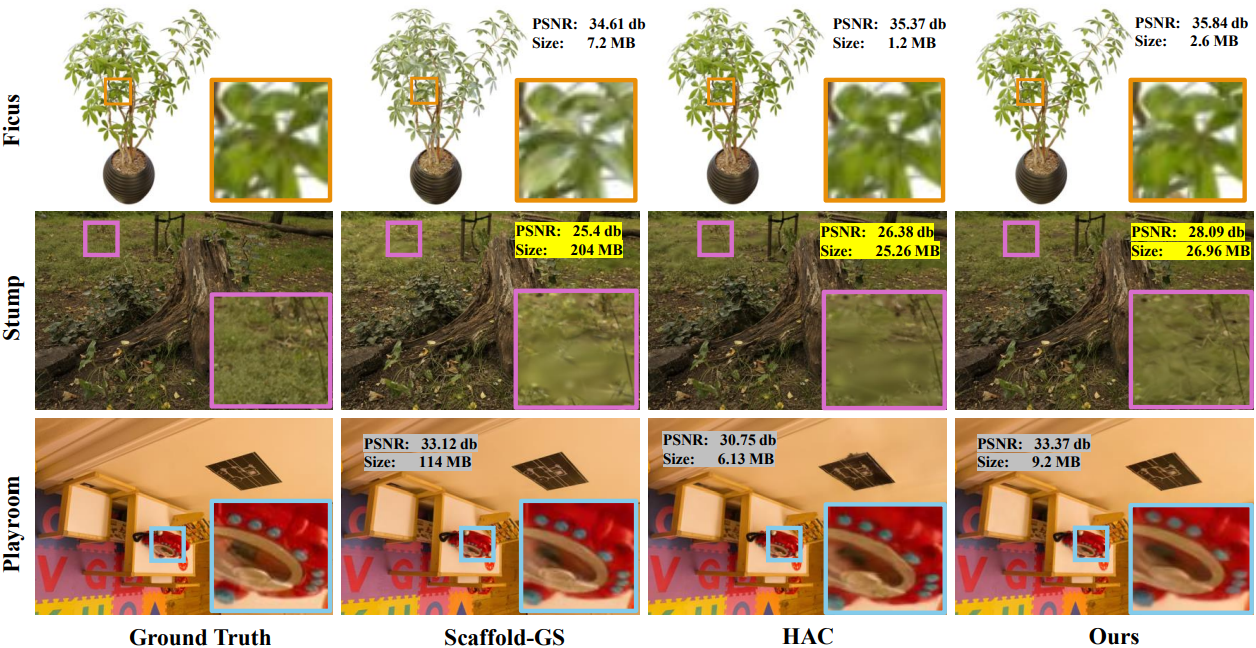
다음은 여러 데이터셋에서의 정성적 결과를 비교한 것이다.

2. Ablation Study

다음은 ablation study 결과이다.

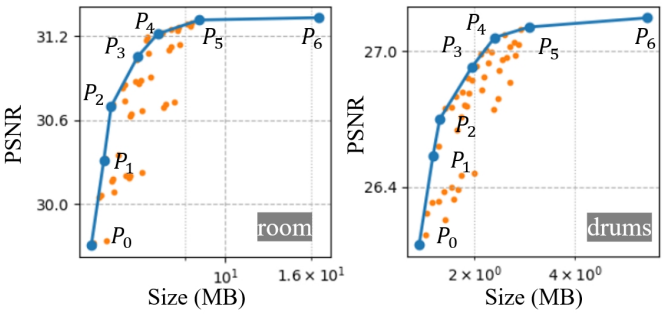
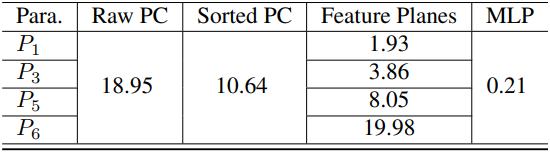
다음은 압축 파라미터에 따른 렌더링 품질과 저장 공간을 비교한 것이다. (표는 Mip-NeRF360의 ‘garden’)

Limitations

1. 공간 수축으로 인한 왜곡은 unbounded scene에서 성능 저하를 일으킬 수 있다.
2. 더 긴 학습 시간이 필요하다. (렌더링 속도는 3DGS와 동일)