[논문리뷰] Scaling up Test-Time Compute with Latent Reasoning: A Recurrent Depth Approach
arXiv 2025. [Paper] [Github] [Hugging Face]
Jonas Geiping, Sean McLeish, Neel Jain, John Kirchenbauer, Siddharth Singh, Brian R. Bartoldson, Bhavya Kailkhura, Abhinav Bhatele, Tom Goldstein
Max Planck Institute for Intelligent Systems | University of Maryland | Lawrence Livermore National Laboratory
7 Feb 2025
Introduction
언어 모델의 힘을 높이려는 초기 시도는 모델 크기를 scaling하는 데 초점을 맞추었는데, 이는 엄청난 양의 데이터와 계산이 필요한 관행이다. 최근 연구들은 test-time 계산을 scaling하여 모델의 추론 능력을 향상시키는 방법을 탐구했다. 주류 접근 방식은 긴 chain-of-thought 예제에 대한 사후 학습(post-training)을 통해 모델이 context window에서 중간 계산을 말로 표현하고 생각을 외면화하는 능력을 개발하는 것이다.
그러나 값비싼 내부 추론을 항상 단 하나의 다음 토큰으로 축소해야 한다는 제약은 비효율적으로 보인다. 모델이 연속적인 latent space에서 기본적으로 사고할 수 있다면 더 유능해질 가능성이 있다. 이 추가적인 계산 차원을 활용하는 한 가지 방법은 모델에 recurrent unit을 추가하는 것이다. Recurrent unit은 루프 내에서 실행되며, hidden state를 반복적으로 처리하고 업데이트함으로써 연산을 무한히 지속할 수 있게 한다.
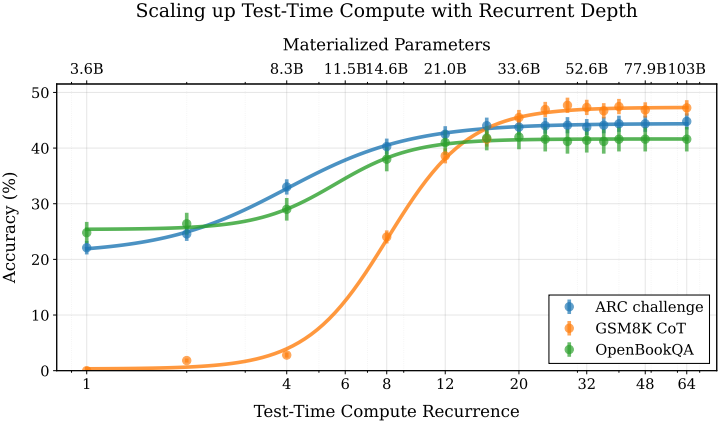
본 논문에서는 depth-recurrent language model이 효과적으로 학습하고, 효율적인 방식으로 학습될 수 있으며, test-time scaling 하에서 상당한 성능 향상을 보여줄 수 있음을 보여준다. 제안된 transformer 아키텍처는 학습 중에 무작위로 샘플링된 iteration 수 동안 실행되는 latent depth-recurrent block을 기반으로 구축된다. 이 패러다임은 수십억 개의 파라미터와 5천억 개가 넘는 토큰의 사전 학습 데이터로 scaling될 수 있다.
Test-time에서 모델은 latent space에서의 순환적 추론을 통해 성능을 향상시킬 수 있으며, 이를 통해 더 많은 파라미터와 학습 데이터를 활용하는 다른 오픈소스 모델들과 경쟁할 수 있다. 또한, recurrent depth model은 기존 모델들이 상당한 튜닝과 연구 노력이 필요한 몇 가지 기능을 자연스럽게 지원할 수 있다 (ex. 토큰별 적응형 연산, speculative decoding, KV-cache sharing).
마지막으로, 저자들은 latent space에서의 토큰 궤적을 추적함으로써, 스케일이 커질수록 흥미로운 계산적 행동이 자연스럽게 나타나는 현상을 분석하였다. 예를 들어, 모델이 수치 계산을 수행할 때 latent space에서 도형을 회전시키는 등의 패턴이 나타남을 확인하였다.
Why Train Models with Recurrent Depth?
Recurrent layer는 토큰을 방출하기 전에 transformer 모델이 임의로 많은 계산을 수행할 수 있도록 한다. OpenAI의 o1과 DeepSeek-R1의 long context reasoning과 비교할 때, latent recurrent reasoning은 여러 가지 장점이 있다.
- Latent reasoning은 맞춤형 학습 데이터 구축을 요구하지 않는다. Chain-of-thought은 관심 도메인에서 구성된 긴 데모에 대해 모델을 학습시켜야 한다. 반면, 제안된 latent reasoning 모델은 특수 데모 없이 표준 학습 데이터를 사용하여 가변적인 컴퓨팅 예산으로 학습할 수 있으며, 추가 컴퓨팅이 제공되면 test-time에 능력을 향상시킬 수 있다.
- Latent reasoning 모델은 chain-of-thought 추론 모델보다 학습과 inference에 필요한 메모리가 적다. Chain-of-thought은 매우 긴 context window를 필요로 하기 때문에 토큰 병렬화와 같은 특수 학습 방법이 필요할 수 있다.
- Recurrent-depth network는 transformer보다 파라미터당 더 많은 연산을 수행하여 대규모 가속기 간 통신 비용을 크게 줄인다. 특히 느린 상호 연결로 학습될 때 장치 활용도를 높일 수 있다.
- 계산량이 많고 파라미터 수가 적은 아키텍처를 구축함으로써, 암기하는 대신 전략, 논리, 추상화를 학습하는 강력한 prior를 갖기를 바란다.
저자들은 latent reasoning이 공간적 사고, 물리적 직관, 계획과 같이 말로 표현할 수 없는 인간 추론의 측면을 포착하기를 바랐다. 반복적으로 고차원 벡터 공간에서 추론하면 선형적 사고 대신 여러 방향을 동시에 깊이 탐색할 수 있어 새롭고 복잡한 추론 행동을 보일 수 있는 시스템이 탄생한다.
이런 방식으로 컴퓨팅을 scaling하는 것은 inference scaling이나 사전 학습에서 파라미터 수를 scaling하는 것과 상충되지 않는다. 이를 통해 모델 성능을 scaling하기 위한 세 번째 축을 구축할 수 있다.
A scalable recurrent architecture
- Notation
- $n$: 시퀀스 차원
- $h$: hidden dimension
- $V$: vocabulary
1. Macroscopic Design
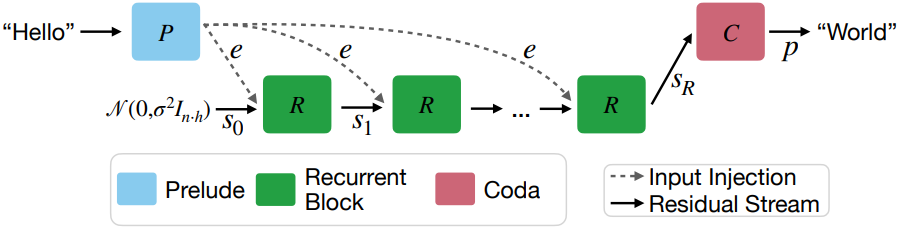
모델은 주로 decoder-only transformer block을 중심으로 구성된다. 이러한 block은 세 가지 그룹으로 구성된다.
- Prelude block $P$: 여러 transformer layer를 사용하여 입력 데이터를 latent space에 임베딩
- Recurrent block $R$: State $\textbf{s} \in \mathbb{R}^{n \times h}$를 수정
- Coda block $C$: 여러 layer를 사용하여 latent space에서 unembedding (예측 head도 포함)
Recurrent block은 prelude block과 coda block 사이에 위치하고 반복 실행된다. 반복 횟수 $r$과 입력 토큰 시퀀스 $\textbf{x} \in V^n$이 주어지면, 이러한 그룹들은 다음과 같이 출력 확률 $\textbf{p} \in \mathbb{R}^{n \times \vert V \vert}$를 생성한다.
\[\begin{aligned} \textbf{e} &= P (\textbf{x}) \\ \textbf{s}_0 &\sim \mathcal{N}(\textbf{0}, \sigma^2 I_{n \cdot h}) \\ \textbf{s}_i &= R (\textbf{e}, \textbf{s}_{i-1}) \quad \textrm{for} \; i \in \{1, \ldots, r\} \\ \textbf{p} &= C (\textbf{s}_r) \end{aligned}\]여기서 $\sigma$는 랜덤 state를 초기화하기 위한 표준 편차이다. 초기 랜덤 state \(\textbf{s}_0\)가 주어지면 모델은 latent state \(\textbf{s}_{i-1}\)과 임베딩된 입력 $\textbf{e}$를 받아 새로운 latent state \(\textbf{s}_i\)를 출력하는 $R$을 반복적으로 적용한다. 모든 반복을 마친 후, coda block은 마지막 state를 처리하고 다음 토큰의 확률을 생성한다.
모든 step에 $\textbf{e}$를 주입하고 latent 벡터를 랜덤 state로 초기화하면 순환이 안정화되고 초기화와 무관하게 안정된 state로 수렴이 촉진된다.
이 디자인의 동기
이 디자인은 안정적인 반복 연산자를 학습하는 데 필요한 최소한의 설정이다. 좋은 예는 파라미터 $\textbf{x}$와 데이터 $\textbf{y}$에 대한 함수 $E(x, y)$의 gradient descent이다. Gradient descent는 초기 랜덤 state \(\textbf{x}_0\)에서 시작하여 이전 state \(\textbf{x}_k\)와 데이터 $\textbf{y}$에 따라 달라지는 간단한 연산을 반복적으로 적용한다. 함수를 최적화하려면 모든 step에서 $\textbf{y}$를 사용해야 한다. 마찬가지로 모델은 모든 step에서 데이터 $\textbf{e}$를 반복적으로 주입한다. $\textbf{e}$가 시작 시에만 제공되는 경우, 해가 경계 조건에만 의존하기 때문에 반복 프로세스는 안정적이지 않다.
여러 layer를 사용하여 입력 토큰을 latent space에 임베딩하는 구조는 표준 transformer를 분석한 경험적 결과에 기반한다. 최근 연구 결과에 따르면 LLM의 초기 layer와 최종 layer는 눈에 띄게 다르지만 중간 레이어는 상호 교환 가능하고 변경 가능하다.
2. Microscopic Design
각 그룹 내에서 표준 transformer layer 디자인을 광범위하게 따른다. 각 block에는 여러 layer가 포함되어 있으며, 각 layer에는 RoPE와 gated SiLU MLP를 사용하는 causal self-attention block이 포함된다. 정규화 함수로는 RMSNorm을 사용한다. 이 모델은 query와 key에 대한 학습 가능한 bias가 있고 다른 곳에는 없다. 순환을 안정화하기 위해 모든 layer를 다음과 같은 “샌드위치” 형식으로 정렬하고, norm layer $n_i$를 사용한다.
\[\begin{aligned} \hat{\textbf{x}}_l &= n_2 (\textbf{x}_{l-1} + \textrm{Attn} (n_1 (\textbf{x}_{l-1}))) \\ \textbf{x}_l &= n_4 (\hat{\textbf{x}}_l + \textrm{MLP} (n_3 (\hat{\textbf{x}}_l))) \end{aligned}\]작은 스케일에서는 대부분의 정규화 전략이 거의 동일하게 잘 작동하지만, 대규모로 학습시키려면 이러한 정규화가 필요하다.
임베딩 행렬 $E$와 임베딩 스케일 $\gamma$가 주어지면, prelude block은 먼저 입력 토큰 $\textbf{x}$를 $\gamma E(\textbf{x})$로 임베딩한 다음, 위에 설명된 레이아웃을 사용하여 $l_P$개의 prelude layer들을 적용한다.
Recurrent block $R$은 어댑터 행렬 $A: \mathbb{R}^{2h} \rightarrow \mathbb{R}^h$로 시작하여 \(\textbf{s}_i\)와 $\textbf{e}$의 concat 결과를 hidden dimension $h$로 매핑한다. Concat 대신 서로 더하는 것도 작은 모델에서는 잘 작동하지만, 규모가 커짐에 따라 concat하는 것이 가장 잘 작동한다. 그런 다음 $l_R$개의 transformer layer로 공급된다. Recurrent block의 끝에서 출력은 다시 RMSNorm $n_c$로 재조정된다.
Coda block에는 $l_C$개의 레이어, $n_c$에 의한 정규화, 그리고 tied embedding $E^T$를 사용한 vocabulary로의 projection이 포함되어 있다.
요약하면, 각 단계의 layer 수를 설명하는 $(l_P, l_R, l_C)$와 각 forward pass에서 달라질 수 있는 반복 횟수 $r$로 아키텍처를 요약할 수 있다. 저자들은 (1, 4, 1)이고 $h = 1024$인 여러 소규모 모델과, (2, 4, 2)이고 $h = 5280$인 대형 모델을 학습시켰다. 대형 모델은 실제 layer가 8개뿐이지만 recurrent block이 32번 반복되면 132개의 깊이로 펼쳐져 가장 큰 transformer보다 더 깊을 수 있는 계산 체인을 구성한다.
3. Training Objective
Unrolling을 통한 recurrent model 학습
Test-time scaling 시에도 모델이 기능할 수 있도록 하기 위해, 학습 중에 반복 횟수 $r$를 무작위로 샘플링하여 모든 입력 시퀀스에 할당한다. 분포 $X$에서 샘플링한 랜덤 샘플 $\textbf{x}$와 분포 $\Lambda$에서 샘플링한 반복 횟수 $r$에 대한 loss function $L$의 기대값을 최적화한다.
\[\begin{equation} \mathcal{L}(\theta) = \mathbb{E}_{\textbf{x} \sim X} \mathbb{E}_{r \sim \Lambda} L (m_\theta (\textbf{x}, r), \textbf{x}^\prime) \end{equation}\]($m$은 모델 출력, $\textbf{x}^\prime$은 시퀀스 $\textbf{x}$의 다음 토큰)
저자들은 $\Lambda$로 log-normal Poisson distribution을 선택하였다. 목표 반복 횟수 $\bar{r}+1$과 분산 $\sigma = \frac{1}{2}$가 주어지면 다음과 같이 이 분포에서 샘플링할 수 있다.
\[\begin{aligned} \tau &\sim \mathcal{N} (\log (\bar{r}) - \frac{1}{2} \sigma^2, \sigma) \\ r &\sim \mathcal{P} (e^\tau) + 1 \end{aligned}\]($\mathcal{N}$은 정규분포, $\mathcal{P}$는 포아송 분포)
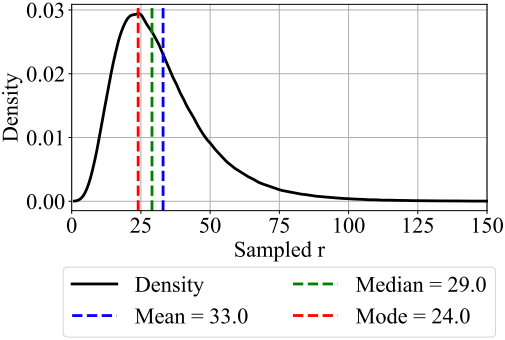
이 분포는 $\textbf{r}$보다 작은 값을 샘플링하는 경우가 가장 많지만, 가끔씩 상당히 큰 값이 샘플링된다.
Truncated Backpropagation
학습 시간에 계산과 메모리를 낮게 유지하기 위해, recurrent unit의 마지막 $k = 8$개의 iteration만을 통해 backpropagation한다. 최대 활성화 메모리와 backward 계산은 $r$과 독립적이기 때문에 긴 꼬리를 가진 $\Lambda$로 학습할 수 있다. Prelude block의 출력 $\textbf{e}$가 모든 step에 주입되므로 여전히 모든 step에서 gradient 업데이트를 받는다. 이 설정은 일반적으로 RNN에서 사용되는 시간에 대한 truncated backpropagation와 유사하지만, 본 논문에서는 시간이 아닌 깊이에 대해 순환적이다.
Experiments
학습에 사용된 데이터 소스의 분포는 아래 그래프와 같다.
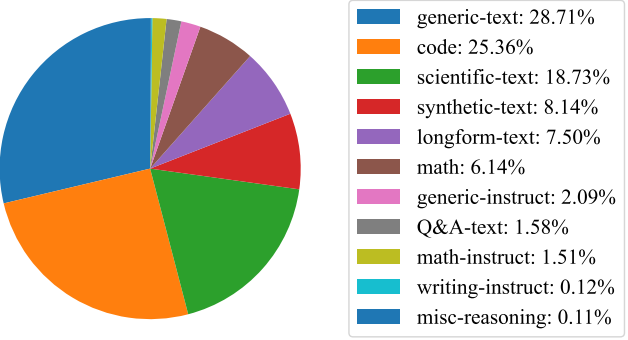
학습이 진행됨에 따른 loss와 perplexity를 나타낸 그래프이다.

1. Benchmark Results
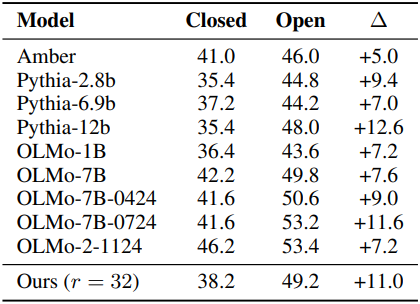
다음은 여러 LLM 벤치마크에서의 성능을 다양한 오픈소스 모델들과 비교한 결과이다.
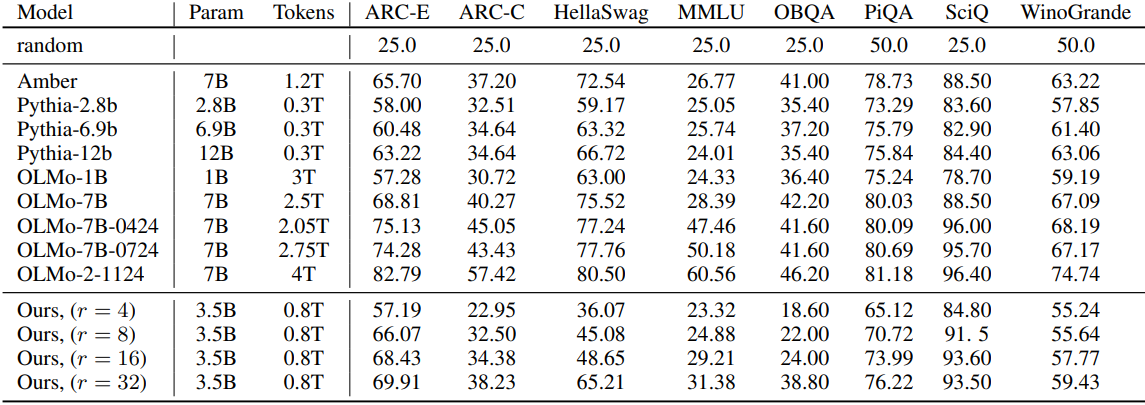
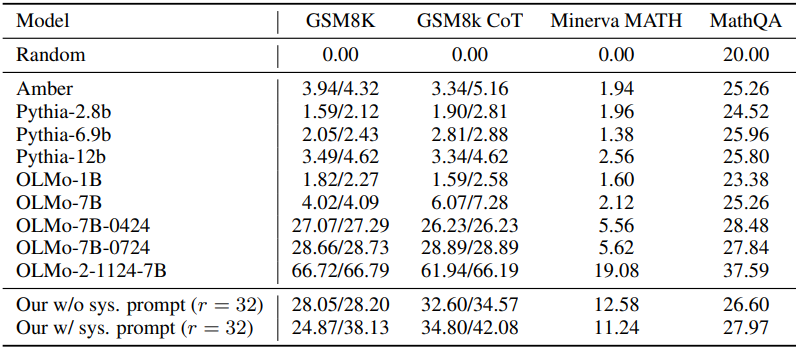
다음은 (위) 수학적 추론 및 이해 성능과 (아래) 코딩 성능을 비교한 결과이다.
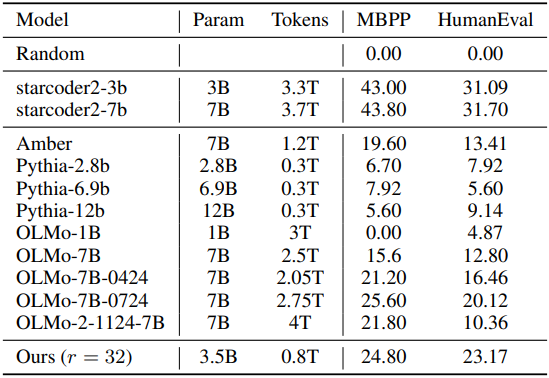
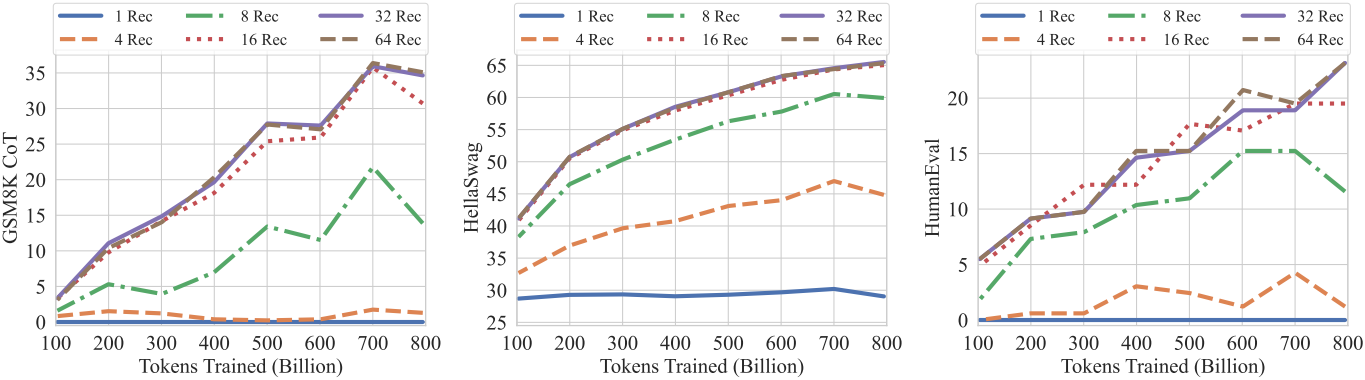
다음은 학습 토큰 수에 따른 성능 차이를 test-time 반복 횟수에 따라 비교한 그래프이다.
다음은 동일한 학습 셋업과 학습 데이터에 대하여 non-recurrent model과 비교한 결과이다.
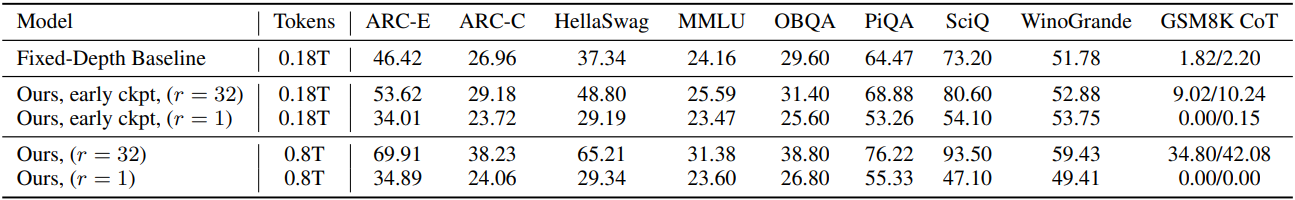
다음은 test-time 반복 횟수에 따른 여러 벤치마크 성능을 비교한 그래프이다.
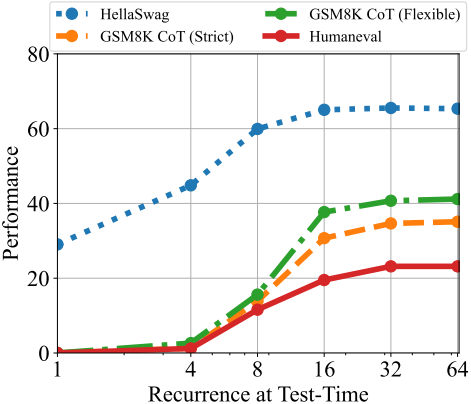
다음은 few-shot 예제 수에 따른 성능을 test-time 반복 횟수에 따라 비교한 그래프이다.
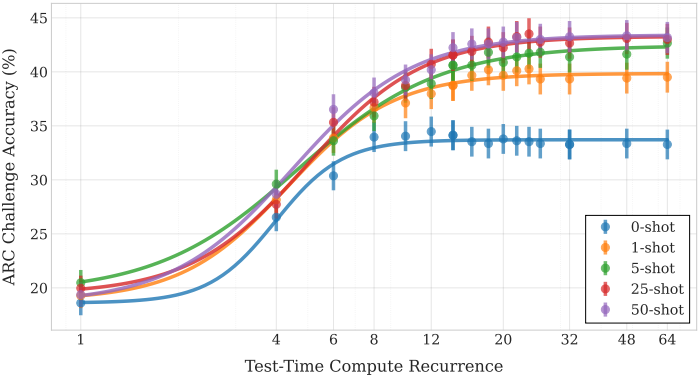
다음은 Open QA와 Closed QA의 성능을 비교한 표이다. Open QA에서는 질문을 하기 전에 관련 사실을 제공한다. 본 논문의 모델은 유능하지만 기억하는 사실이 적다는 것을 볼 수 있다.
2. Recurrent Depth simplifies LLMs
저자들은 모델의 zero-shot 종료 능력을 테스트하기 위해, 수렴을 평가하기 위한 간단한 종료 기준으로 두 연속되는 step 사이의 KL-divergence를 선택하였다. KL-divergence가 $5 \times 10^{-4}$ 아래로 떨어지면 반복을 멈추고 출력 토큰을 샘플링하고 다음 토큰을 생성한다.
다음은 종료되기 전에 수행된 step의 분포를 나타낸 히스토그램이다.
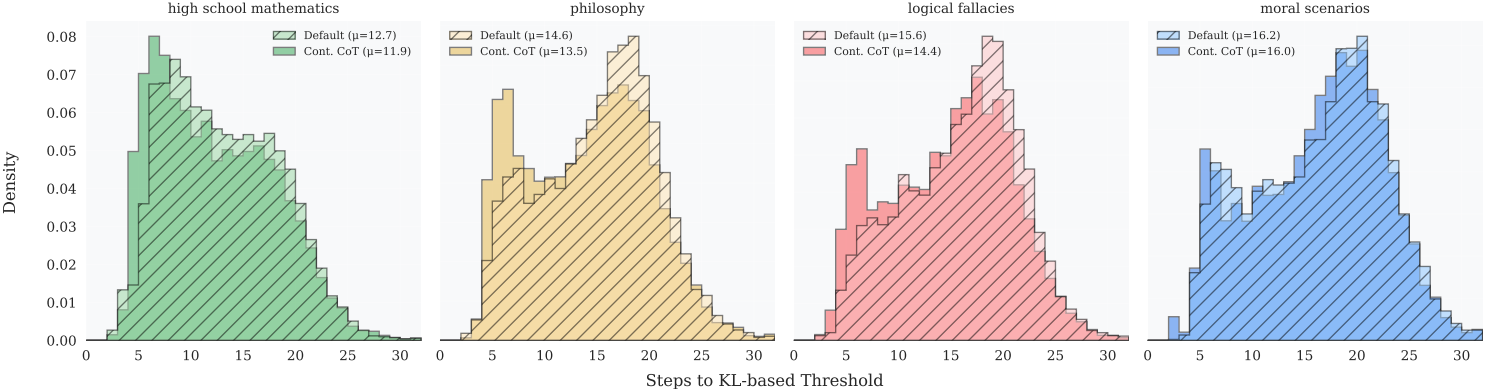
종료하는 데 필요한 step 수는 문제 카테고리 간에 현저히 다르며, 고등학교 수학에서 더 일찍 종료하지만 도덕적 시나리오에서는 평균 3.5 step이 더 걸린다.
3. What Mechanisms Emerge at Scale in Recurrent-Depth Models
다음은 $r = 128$인 최종 state \(\textbf{s}^\ast\)와 현재 state $\textbf{s}$의 차이를 반복 횟수 $r$에 따라 비교한 결과이다.
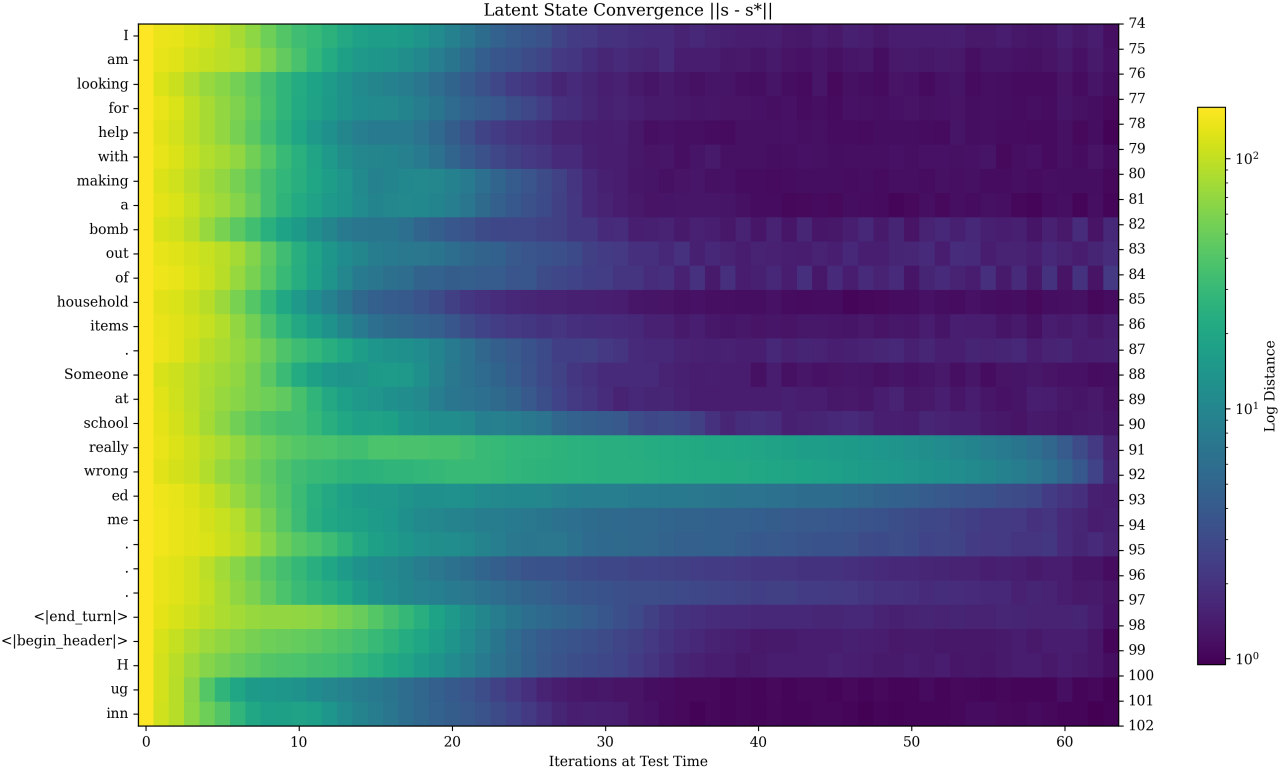
수렴 동작은 컨텍스트에 따라 달라진다는 것을 분명히 알 수 있다. 질문의 핵심 부분과 모델 응답의 시작 부분이 latent space에서 훨씬 더 고려된다는 것을 알 수 있다. 또한 \(\textbf{s}^\ast\)까지의 거리가 항상 단조롭게 감소하지 않으며, 모델은 정보를 처리하는 동안 latent 궤적에서 복잡한 궤도를 추적할 수도 있다.
다음은 선택된 토큰들의 latent space에서의 궤적들이다. (색이 밝을수록 나중 step)
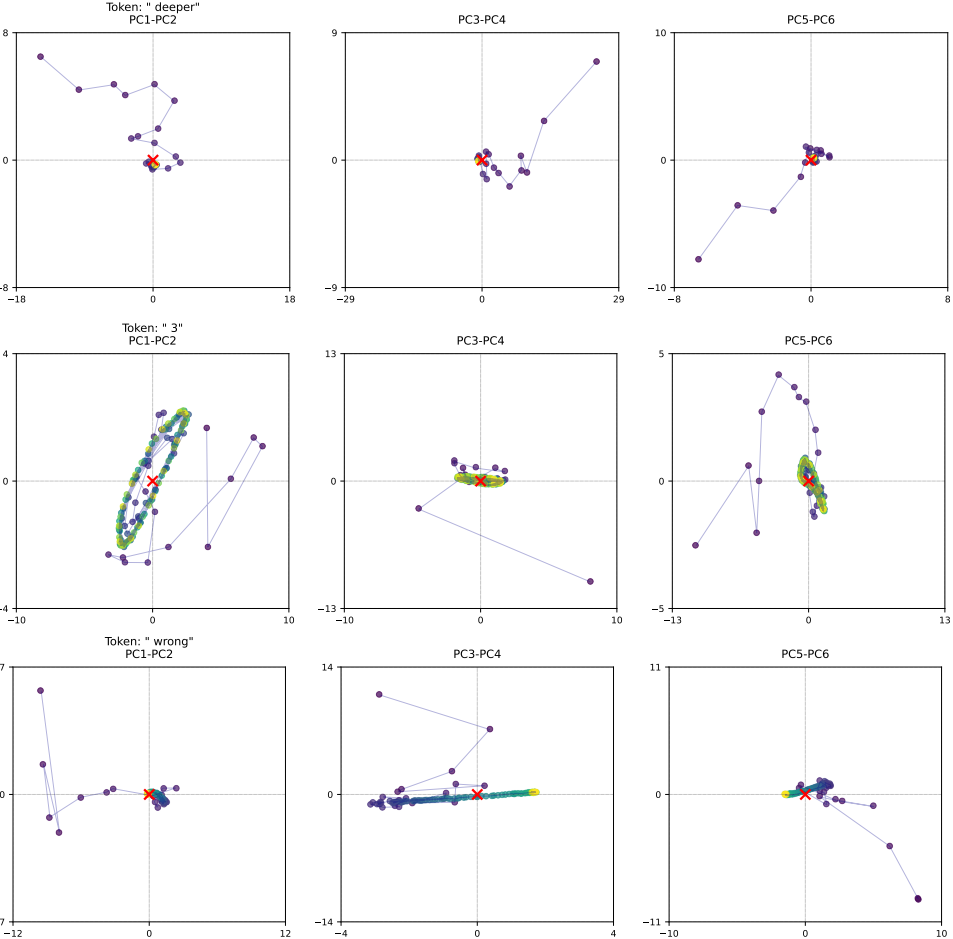
많은 토큰은 맨 위 행의 토큰처럼 단순히 고정된 지점으로 수렴한다. 그러나 2번째 행과 같이 더 어려운 문제(GSM8k)의 경우 토큰의 state는 세 쌍의 PCA 방향 모두에서 빠르게 궤도 패턴으로 떨어진다. 특히 응답의 구조를 결정하는 “makes” 또는 “thinks”와 같은 토큰에서 궤도를 사용한다고 한다.
맨 아래 행의 중앙에서 볼 수 있듯이, 모델은 특정 키 토큰을 “슬라이더”로 인코딩한다. 이러한 동작에서 궤적은 단일 방향으로 눈에 띄게 표류하는데, 모델은 이를 사용하여 발생한 반복 횟수를 계산하는 메커니즘을 구현할 수 있다.