Diffusion은 신이고 GPT는 무적이다

arXiv 2022. [Paper] [Page]
Naoya Takahashi, Mayank Kumar, Singh, Yuki Mitsufuji
Sony Group Corporation
14 Oct 2022

Introduction

Neural vocoder는 신경망을 이용하여 음향적 feature로부터 waveform을 생성하고 음성 신호의 효율적인 모델링을 위해 종종 음향적 feature 도메인에서 작동하기 때문에 TTS, 음성 변환, 음성 향상과 같은 많은 음성 처리 task에 필수적인 구성 요소가 되었다. Autoregressive model, GAN, flow-based model과 같은 여러 생성 모델이 neural vocoder에 채택되었다.

Diffusion model은 nueral vocoder에 채택되어 왔다. Diffusion model은 고품질 음성 데이터를 생성하는 것으로 나타났지만 데이터 생성을 위해 많은 iteration이 필요하기 때문에 다른 autoregressive model 기반이 아닌 vocoder에 비해 inference 속도가 상대적으로 느리다. PriorGrad는 데이터 종속 prior, 특히 entry가 mel-spectrogram의 프레임별 에너지인 대각 공분산 행렬을 사용하는 가우시안 분포를 도입하여 이 문제를 해결하였다. 데이터 종속 prior에서 가져온 noise가 표준 Gaussian의 noise보다 타겟 waveform에 더 가깝기 때문에 PriorGrad는 우수한 성능으로 더 빠른 수렴과 inference를 달성한다. SpecGrad는 타겟 신호와 더 유사한 noise를 도입하기 위해 mel-spectrogram의 spectral envelope를 통합하여 prior을 추가로 개선하였다.

그러나 기존의 많은 neural vocoder는 음성 신호에 중점을 둔다. 저자들은 state-of-the-art neural vocoder가 노래하는 목소리에 적용될 때 품질이 불충분하다는 것을 발견했다. 아마도 대규모의 깨끗한 가창 음성 데이터셋이 부족하고 음악적 표현으로 인해 음조, 음량, 발음이 더 다양해 모델링하기가 더 어렵기 때문일 수 있다.

본 논문은 이 문제를 극복하기 위해 서로 다른 샘플링 속도에서 여러 diffusion model을 학습하는 계층적 diffusion model을 제안한다. Diffusion model은 음향 feature과 더 낮은 샘플링 속도의 데이터로 컨디셔닝되며 병렬로 학습될 수 있다. Inference하는 동안 모델은 낮은 샘플링 속도에서 높은 샘플링 속도로 점진적으로 데이터를 생성한다. 가장 낮은 샘플링 속도에서의 diffusion model은 정확한 피치 복구를 위한 저주파 구성 요소 생성에 초점을 맞추는 반면, 더 높은 샘플링 속도에서는 고주파 디테일에 더 집중한다. 이것은 노래하는 목소리의 강력한 모델링 능력을 가능하게 한다. 본 실험에서는 제안한 방법을 PriorGrad에 적용하여 제안한 모델이 최신 PriorGrad와 Parallel WaveGAN vocoder를 능가하는 여러 가수의 고품질 노래 음성을 생성함을 보여준다.

Prior Work

1. DDPM

Forward process:

\[\begin{equation} q(x_{1:T} \vert x_0) = \prod_{t=1}^T q(x_t \vert x_{t-1}) \\ q(x_t \vert x_{t-1}) := \mathcal{N} (x_t; \sqrt{1 - \beta_t} x_{t-1}, \beta_t I) \end{equation}\] \[\begin{equation} x_t = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{(1 - \bar{\alpha}_t)} \epsilon \\ \alpha_t = 1 - \beta_t, \quad \bar{\alpha}_t = \prod_{s=1}^t \alpha_s \end{equation}\]

Reverse process:

\[\begin{equation} p(x_{0:T}) = p(x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t) \\ p_\theta (x_{t-1} \vert x_t) := \mathcal{N} (x_{t-1}; \mu_\theta (x_t, t), \sigma_\theta^2 (x_t, t) I) \\ \mu_\theta (x_t, t) = \frac{1}{\sqrt{\alpha_t}} (x_t - \frac{\beta_t}{\sqrt{1 - \bar{\alpha}_t}} \epsilon_\theta (x_t, t)) \sigma_\theta^2 (x_t, t) = \frac{1 - \bar{\alpha}_{t-1}}{1 - \bar{\alpha}_t} \beta_t \end{equation}\]

ELBO:

\[\begin{equation} \textrm{ELBO} = C - \sum_{t=1}^T \kappa_t \mathbb{E}_{x_0, \epsilon} [\| \epsilon - \epsilon_\theta (x_t, t) \|^2] \\ \kappa_t = \frac{\beta_t}{2 \alpha (1 - \bar{\alpha}_{t-1})} \end{equation}\]

2. PriorGrad

PriorGrad는 적응형 prior $\mathcal{N}(0, \Sigma_c)$를 사용하며, 여기서 대각 분산 행렬 $\Sigma_c$는 mel-spectrogram $c$로부터 다음과 같이 계산된다.

\[\begin{equation} \Sigma_c = \textrm{diag}[(\sigma_0^2, \cdots, \sigma_L^2)] \end{equation}\]

여기서 $\sigma_i^2$은 $i$번째 샘플에서의 mel-spectrogram의 프레임 레벨 에너지를 정규화한 것이다. 수정된 loss function은 다음과 같다.

\[\begin{equation} L = \mathbb{E}_{x_0, \epsilon, t} [\|\epsilon - \epsilon_\theta (x_t, c, t) \|_{\Sigma^{-1}}^2] \end{equation}\]

여기서 $|x|_{\Sigma^{-1}}^2 = x^\top \Sigma^{-1} x$이다.

Proposed Method

1. Hierarchical diffusion probabilistic model

PriorGrad는 음성 데이터에서 유망한 결과를 보여주지만 노래하는 목소리에 적용할 때 음조, 음량, 비브라토, 가성과 같은 음악적 표현이 더 다양하기 때문에 품질이 만족스럽지 못하다. 이 문제를 해결하기 위해 본 논문은 노래하는 목소리를 여러 해상도로 모델링하여 diffusion model 기반 neural vocoder를 개선할 것을 제안하였다. 제안된 방법의 개요는 아래와 같다.


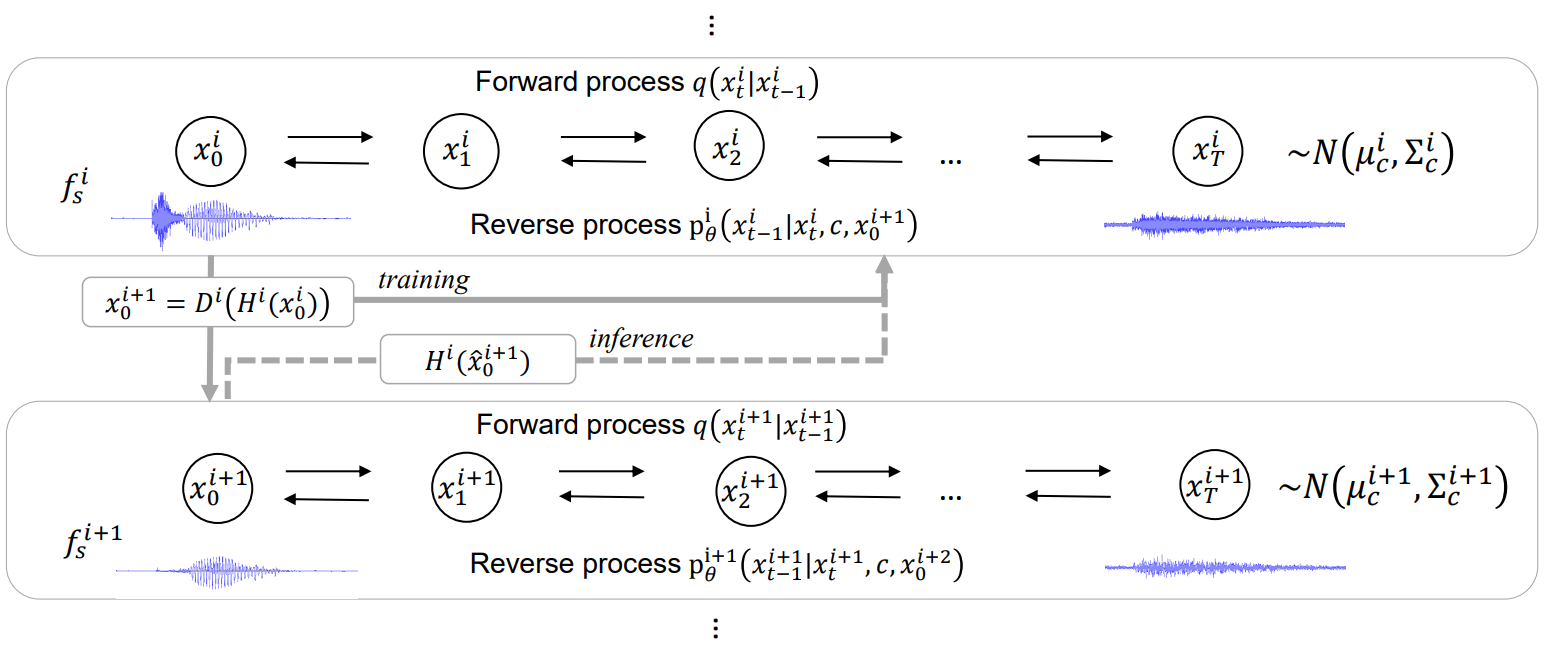
여러 샘플링 속도 $f_s^1 > f_s^2 > \cdots > f_s^N$가 주어지면 각 샘플링 속도에서 독립적으로 diffusion model을 학습한다. 각 샘플링 속도 $f_s^i$에서의 reverse process는 일반적인 음향 feature $c$와 더 낮은 샘플링 속도 $f_s^{i+1}$의 데이터를

\[\begin{equation} p_\theta^i (x_{t-1}^i \vert x_t^i, c, x_0^{i+1}) \end{equation}\]

와 같이 컨디셔닝한다. 가장 샘플링 속도가 낮은 모델에서는 $c$에 대해서만 컨디셔닝된다. 학습 중에 noise 추정 모델 $\epsilon_\theta^i (x_t^i, c, x_0^{i+1}, t)$를 컨디셔닝하기 위해 ground-truth 데이터 $x_0^{i+1} = D^i (H^i (x_0^i))$를 사용한다. 여기서 $H^i (\cdot)$는 안티 앨리어싱 필터를 나타내고 $D^i(\cdot)$은 샘플링 속도가 $f$인 신호에 대한 다운샘플링 함수를 나타낸다. Noise가 원래 데이터 $x_0$에 선형적으로 추가되고 모델이 실제 낮은 샘플링 속도의 ground-truth 데이터 $x_0^{i+1}$에 직접 액세스할 수 있으므로 모델은 복잡한 음향 feature-waveform 변환을 피함으로써 $x_t^i$와 $x_0^{i+1}$의 저주파에 대한 noise를 더 간단하게 예측할 수 있다. 이를 통해 모델은 고주파 구성 요소의 변환에 더 집중할 수 있다. 가장 낮은 샘플링 속도 $f_s^N$(실험에서는 6kHz 사용)에서 데이터 $x_0^N$은 원래 샘플링 속도보다 훨씬 단순해지며 모델은 노래하는 목소리의 정확한 피치 복구를 위한 저주파 성분 생성에 집중할 수 있다.

Inference하는 동안 가장 낮은 샘플링 속도 \(\hat{x}_0^N\)에서 데이터를 생성하는 것으로 시작하여 생성된 샘플 \(\hat{x}_0^{i+1}\)을 조건으로 사용하여 더 높은 샘플링 속도 \(\hat{x}_0^i\)에서 데이터를 점진적으로 생성한다.


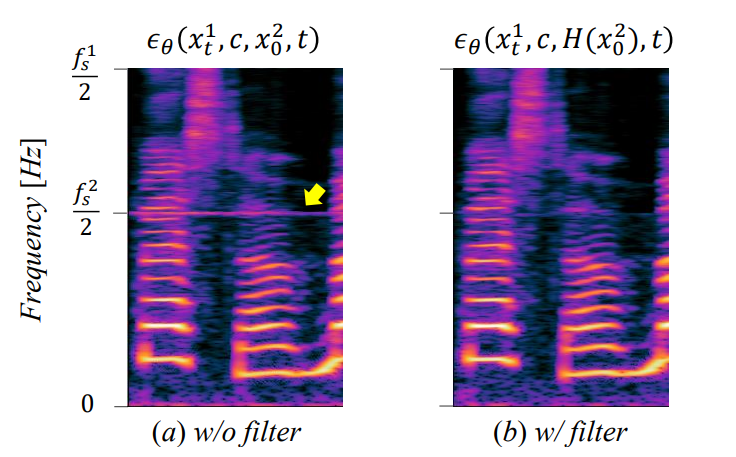
실제로 \(\hat{x}_0^{i+1}\)을 조건으로 직접 사용하면 위 그림의 (a)와 같이 각 샘플링 속도 $f_s^2 / 2, \cdots, f_s^N / 2$의 Nyquist 주파수 주변에서 노이즈가 자주 발생한다. 이는 학습과 inference 사이의 차이 때문이다. 학습에 사용되는 ground-truth 데이터 $x_0^{i+1} = D^i (H^i (x_0^i))$는 안티 앨리어싱 필터로 인해 Nyquist 주파수 주변의 신호를 포함하지 않으며 모델은 신호를 직접 사용하는 방법을 학습할 수 있다. Nyquist 주파수는 \(\hat{x}_0^{i+1}\) 추론에 사용되는 생성된 샘플이 불완전한 예측으로 인해 주변에 일부 신호를 포함할 수 있고 더 높은 샘플링 속도에서 예측을 오염시킬 수 있다. 이 문제를 해결하기 위해 생성된 더 낮은 샘플링 속도 신호에 안티 앨리어싱 필터를 적용하여 noise 예측 모델을 다음과 같이 컨디셔닝한다.

\[\begin{equation} \hat{\epsilon} = \epsilon_\theta^i (x_t^i, c, H(\hat{x}_0^{i+1}), t) \end{equation}\]

위 그림의 (b)와 같이 Nyquist 주파수 주변의 noise를 제거하고 품질을 향상시킨다. PriorGrad와의 결합에 대한 학습 및 inference 절차는 각각 Algorithm 1과 2와 같다.

제안된 계층적 diffusion model은 DiffWave, PriorGrad, SpecGrad 등 다양한 종류의 diffusion model과 결합할 수 있다.

2. Network architecture

PriorGrad에서와 마찬가지로 모델 아키텍처는 DiffWave를 기반으로 한다. 네트워크는 양방향 dilated convolution과 repeated dilation factors가 있는 $L$개의 residual layer로 구성된다. 레이어는 $m$ 블록으로 그룹화되며 각 블록은 $l = L/m$ 레이어로 구성되며 dilated factor는 $[1, 2, \cdots, 2^{l-1}]$이다. DiffWave와 PriorGrad는 $L = 30$, $l = 10$을 사용하여 큰 receptive field를 처리한다. 본 논문의 접근 방식은 더 낮은 샘플링 속도에서 모델링을 활용할 수 있으며 더 작은 네트워크는 긴 신호 길이를 몇 초 만에 처리할 수 있다. 따라서 다중 해상도 모델링으로 인한 계산 비용 증가를 완화하기 위해 다른 샘플링 속도의 모든 모델에 대해 크기를 $L = 24$, $l = 8$로 줄인다. 이 hyperparameter는 N = 2일 때 원래 diffusion model과 거의 동일한 계산 비용을 제공한다.


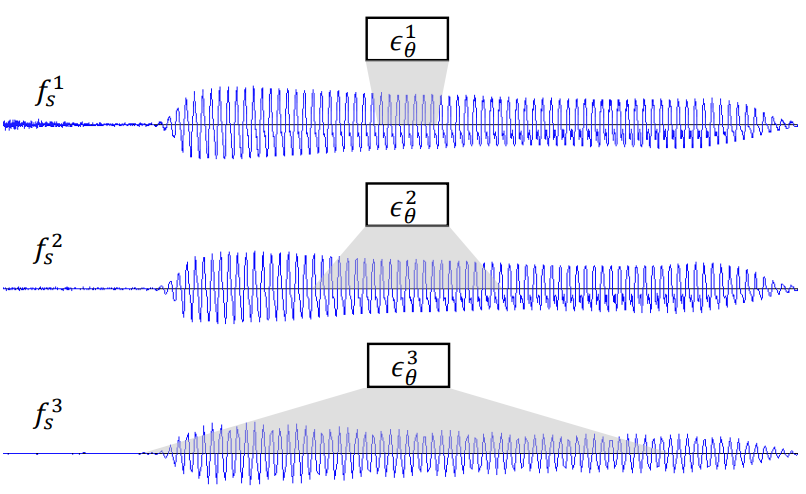
모든 샘플링 속도에 대해 동일한 네트워크 아키텍처를 사용하면 샘플링 속도에 따라 모델의 receptive field가 효과적으로 변경된다. 더 낮은 샘플링 속도에서 모델은 더 긴 duration을 다루고 저주파 구성 요소에 초점을 맞추는 반면, 더 높은 샘플링 속도에서 모델은 더 짧은 duration을 다루고 고주파 구성 요소에 초점을 맞춘다. 이 설계는 계층적 diffusion model의 의도와 일치한다. 왜냐하면 모델은 더 낮은 샘플링 속도 $x_0^{i+1}$에서 Nyquist 주파수 $f_s^{i+1} / 2$까지 컨디셔닝된 데이터를 직접 사용하고 음향 feature를 고주파에서 파형으로 변환하는 데 집중할 것으로 예상되기 때문이다.

Experiments

  • 데이터셋: NUS48E, NHSS, 내부 corpus
  • Hyperparameters
    • DiffWave와 PriorGrad를 따름
      • 100만 step 학습
      • batch size 16
      • learning rate $2 \times 10^{-4}$
      • Adam optimizer
    • 80-band mel-spectrogram의 log-scale을 음향 feature로 사용
    • FFT size = 2048, hop size = 300
    • 계층적 diffusion model을 PriorGrad에 적용한 2가지 모델을 구성
      • 2-stage Hierarchical PriorGrad (HPG-2): $(f_s^1, f_s^2) = (24k, 6k)$
      • 3-stage Hierarchical PriorGrad (HPG-3): $(f_s^1, f_s^2, f_s^3) = (24k, 12k, 6k)$
    • Inference noise schedule: $[0.0001, 0.001, 0.01, 0.05, 0.2, 0.5]$ ($T_\textrm{infer} = 6$)
  • Metrics
    • 주관적 평가: 5점으로 자연스러움을 평가 (MOS)
    • 객관적 평가
      • real time factor (RTF)
      • pitch mean absolute error (PMAE)
      • voicing decision error (VDE)
      • multi-resolution STFT error (MR-STFT)
      • Mel cepstral distortion (MCD)

Results

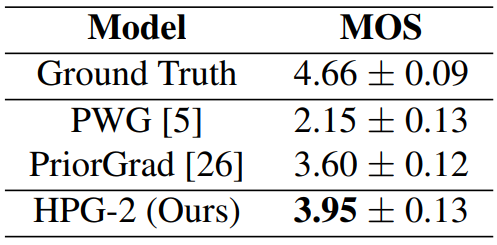
다음은 95% 신뢰 구간의 MOS 결과이다.


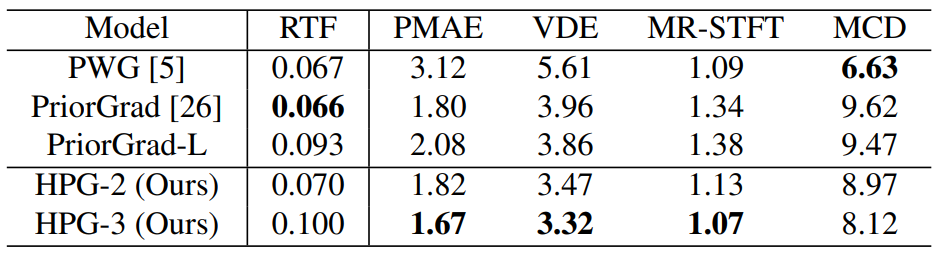
다음은 객관적 평가 결과이다. (모두 낮을수록 좋음)


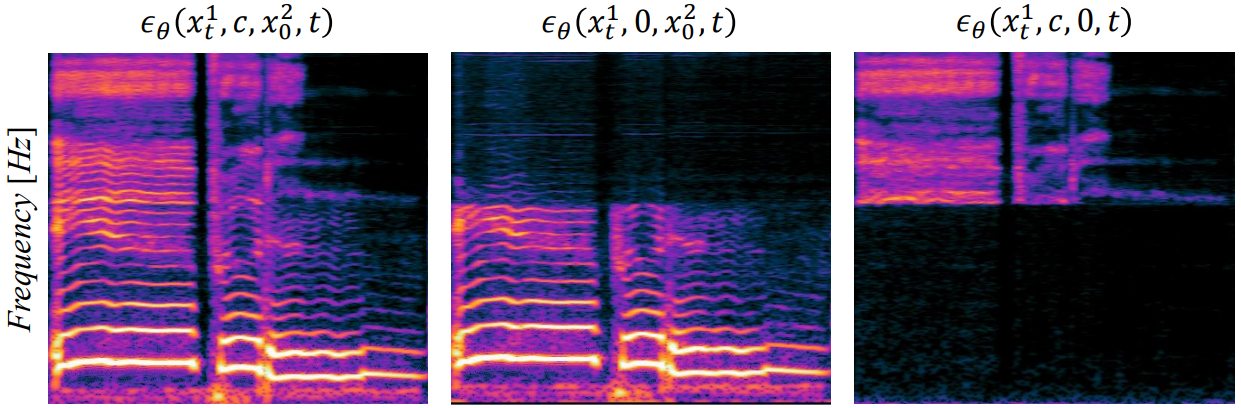
다음은 서로 다른 컨디셔닝에 대하여 생성된 데이터의 spectrogram이다.

You may also enjoy