Diffusion은 신이고 GPT는 무적이다

NeurIPS 2024. [Paper] [Github]
Tuomas Kynkäänniemi, Miika Aittala, Tero Karras, Samuli Laine, Timo Aila, Jaakko Lehtinen
Aalto University | NVIDIA
11 Apr 2024

Introduction

Diffusion model은 denoising process를 반복적으로 적용하여 순수한 noise로 이루어진 초기 이미지를 새로운 생성된 이미지로 변환한다. 이러한 샘플링 과정은 일반적으로 수십 step으로 구성되며, 각 step에서 denoising된 결과 이미지의 일부가 noise가 포함된 이미지에 혼합된다. 샘플링 과정은 먼저 학습 데이터의 평균값으로 수렴한 후, 남아있는 noise를 기반으로 feature를 점진적으로 근사해간다. 이미지가 조금씩 형성되는 이러한 반복적인 과정은 각 step에서 특정 동작을 유도하거나 억제하는 데 상당한 유연성을 제공한다.

부정적 프롬프트는 샘플링 과정에 피해야 할 추가적인 anti-goal을 부여하는 널리 사용되는 개념이다. 모든 샘플링 step에서 denoiser는 긍정적 프롬프트와 부정적 프롬프트에 대해 각각 한 번씩, 총 두 번 실행된다. 그런 다음 가중치 파라미터를 기반으로 긍정적 결과가 부정적 결과에서 더 멀어지도록 extrapolation한다. 이 방식은 실제로 매우 효과적이다. Classifier-free guidance (CFG)는 이러한 일반적인 개념을 기반으로 한다. CFG는 unconditional model을 부정적 프롬프트로 사용하여 결과 이미지가 컨디셔닝 신호에 더 강하게 정렬되도록 한다.

실제로 모든 대규모 이미지 생성 모델은 CFG에 크게 의존한다. CFG는 생성된 이미지 분포를 수학적으로 정당화된 방식으로 제한하여, 기본적으로 시각적으로 더 나은 이미지 품질을 얻는 대신 변동성을 희생한다. 모든 샘플링 step에서 동일한 guidance 가중치가 사용되는데, CFG는 noise level에 따라 매우 다르게 동작하기 때문에 이는 최적의 방식이 아니다. Noise level이 높을 때는 결과의 변동성을 급격히 감소시켜 프롬프트당 몇 개의 “템플릿 이미지”로 수렴하게 만든다. Noise level이 중간일 때는 샘플링이 특정 feature 집합을 더 확실하게 선택하게 하여 더 선명하고 시각적으로 더 만족스러운 결과를 제공한다. Noise level이 낮을 때는 이러한 방식이 거의 필요하지 않다.

본 논문에서는 guidance의 사용을 효과가 긍정적인 중간 샘플링 step들로 제한하고, guidance 가중치는 변경하지 않는 방식을 제안하였다. 이를 통해 guidance의 부정적인 영향을 대부분 방지하고 계산 비용을 절감할 수 있다. 최적의 guidance interval을 적용하였을 때, ImageNet-512에서 FID가 1.81에서 1.40으로 향상되고 시각적 품질 또한 개선되었다. 이러한 이점은 다양한 샘플러 파라미터, 네트워크 아키텍처, 데이터셋에서 일관되게 나타난다.

Background


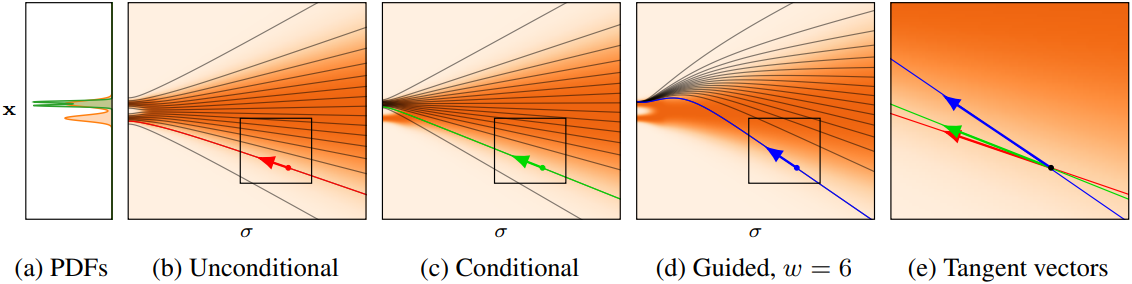
위 그림은 본 논문에서 다루는 개념을 1D 합성 예제를 통해 설명한다. 이 예제에서는 학습된 denoiser가 유발할 수 있는 모든 근사치를 배제하고 이상적인 denoiser를 사용하여 생성을 수행하였다. 이러한 시나리오에서는 CFG가 해롭지만, 이 예제를 통해 CFG가 초래하는 문제점을 직관적으로 시각화할 수 있다.

Diffusion model의 목표는 데이터 분포 \(p_\textrm{data} (\textbf{x})\)에서 샘플을 추출하는 것이다. 일련의 평활화된 분포 $p(\textbf{x}; \sigma)$를 정의해 보자. 각 개별 분포는 \(p_\textrm{data}\)와 표준 편차 $\sigma$를 갖는 Gaussian noise 분포의 convolution이다. EDM 공식에 따르면, $\sigma$ 변화에 따른 샘플 \(\textbf{x} \sim p(\textbf{x}; \sigma)\)의 변화는 다음과 같은 상미분 방정식(ODE)으로 기술된다.

\[\begin{equation} \frac{\textrm{d} \textbf{x}}{\textrm{d} \sigma} = - \frac{D_\theta (\textbf{x}; \sigma) - \textbf{x}}{\sigma} \end{equation}\]

\(D_\theta\)는 아래와 같은 $L_2$ error를 최소화하는 denoiser 모델이다.

\[\begin{equation} \mathbb{E}_{\textbf{y} \sim p_\textrm{data}, \sigma \sim p_\textrm{train}, \textbf{n} \sim \mathcal{N}(\textbf{0}, \sigma^2 \textbf{I})} \| D_\theta (\textbf{y} + \textbf{n}; \sigma) - \textbf{y} \|_2^2 \end{equation}\]

데이터 분포에서 샘플을 생성하기 위해 먼저 초기 샘플 \(\textbf{x}_0 ∼ p(\textbf{x}; \sigma_\textrm{max})\)를 추출한다. 여기서 \(\sigma_\textrm{max}\)는 \(p(\textbf{x}; \sigma_\textrm{max})\)가 순수 Gaussian 분포와 거의 같아 샘플링이 용이하도록 충분히 크게 선택한다. 그런 다음 ODE를 따라 \(\textbf{x}_0\)를 $\sigma = 0$, 즉 데이터 분포로 진화시킨다.

CFG는 conditional ODE와 unconditional ODE의 선형 결합으로 정의되는 \(\textrm{d} \textbf{x} / \textrm{d} \sigma\)를 가지는 수정된 ODE를 구성하는 것으로 생각할 수 있다.

\[\begin{aligned} \frac{\textrm{d} \textbf{x}}{\textrm{d} \sigma} &= w \left( - \frac{D_\theta (\textbf{x} \vert \textbf{c}; \sigma) - \textbf{x}}{\sigma} \right) + (1 - w) \left( - \frac{D_\theta (\textbf{x}; \sigma) - \textbf{x}}{\sigma} \right) \\ &= - \frac{w D_\theta (\textbf{x} \vert \textbf{c}; \sigma) + (1 - w) D_\theta (\textbf{x}; \sigma) - \textbf{x}}{\sigma} \end{aligned}\]

($w$는 guidance 가중치, $c$는 denoiser \(D_\theta\)에 제공되는 조건 정보)

$w > 1$로 설정하면 샘플이 unconditional한 결과에서 효과적으로 벗어나게 된다. 이러한 extrapolation은 직관적으로 조건과 가장 잘 일치하는 영역에 확률 질량을 집중시키려는 의도이다. 그러나 이러한 과도한 조향은 궤적을 데이터 분포에서 벗어나게 하여 mode drop을 유발할 수 있다.

ODE의 샘플링은 noise level을 최대값 \(\sigma_\textrm{max}\)에서 0으로 낮추는 여러 discrete step을 통해 수행되며, 이를 통해 각각 noise level \(\sigma_i\)를 갖는 일련의 이미지 \(\textbf{x}_0, \textbf{x}_1, \ldots, \textbf{x}_N\)이 생성된다. 다양한 discretization 방식과 solver가 제안되어 왔으며, 방식에 관계없이 계산 비용은 샘플링 step 수 $N$에 정비례한다.

Method


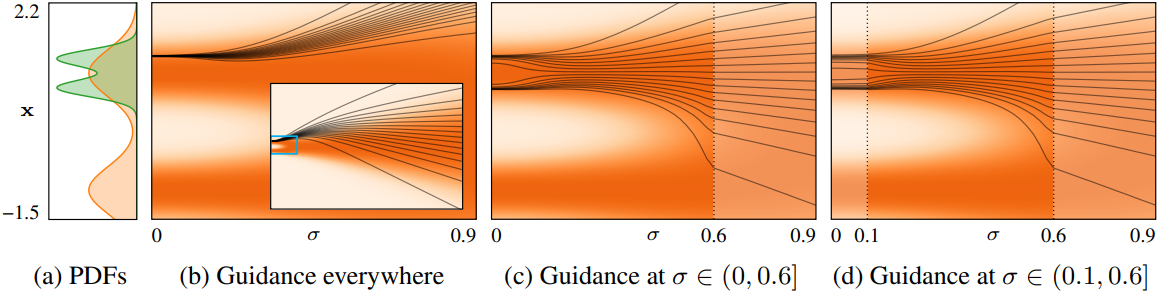
위 그림은 앞서 제시한 간단한 예제를 사용하여 CFG의 단점을 살펴본 것이다. 일반적으로 모든 noise level에서 guidance를 적용하면 샘플링 궤적이 데이터 분포에서 상당히 벗어나는 것을 확인할 수 있다. 이는 unconditional 궤적이 guidance를 받은 궤적을 효과적으로 밀어내어 심하게 왜곡된 중간 분포를 생성하기 때문이다. 결과적으로 샘플러는 mode 중 하나를 완전히 놓치게 된다.

대부분의 편차가 높은 noise level에서 발생하는 것으로 보이므로, (c)에서는 해당 샘플링 step에서 CFG를 비활성화하였다. 이렇게 하면 조건부 분포의 두 가지 mode가 모두 정확하게 복구된다. 또한, (d)와 같이 낮은 noise level에서 guidance를 비활성화해도 결과 분포에 미치는 영향은 미미하여 출력에 최소한의 영향만 주면서 샘플링 비용을 줄일 수 있다. 이 예시는 매우 단순화된 것이지만, 저자들은 실제 규모의 diffusion model에서도 이와 유사한 효과가 나타날 것이라고 가정하였다.

위의 관찰 결과를 바탕으로, 저자들은 샘플링의 중간 부분에서만 guidance를 적용하고 다른 부분에서는 비활성화하는 방안을 제안하였다. 구체적으로, CFG의 ODE에서 $w$를 구간별 상수 함수로 대체하여 재정의한다.

\[\begin{equation} \frac{\textrm{d} \textbf{x}}{\textrm{d} \sigma} = - \frac{w (\sigma) D_\theta (\textbf{x} \vert \textbf{c}; \sigma) + (1 - w (\sigma)) D_\theta (\textbf{x}; \sigma) - \textbf{x}}{\sigma} \\ \textrm{where} \quad w (\sigma) = \begin{cases} w & \textrm{if} \; \sigma \in (\sigma_\textrm{lo}, \sigma_\textrm{hi}] \\ 1 & \textrm{otherwise} \end{cases} \end{equation}\]

이 공식에서 기존 CFG는 \(\sigma_\textrm{lo} = 0\), \(\sigma_\textrm{hi} = \infty\)에 해당한다.

Experiments

1. Main results

다음은 ImageNet-512에서 CFG와 guidance interval을 비교한 결과이다.

2. Ablations

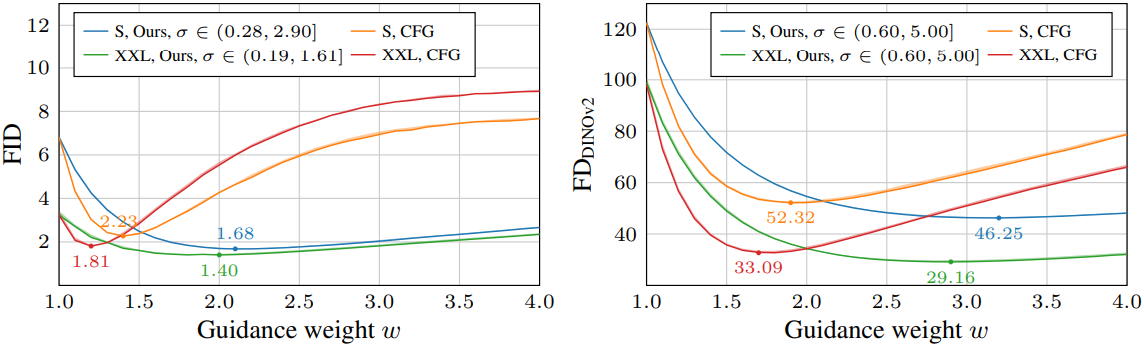
다음은 guidance 가중치에 따른 FID와 FDDINOv2를 나타낸 그래프이다.


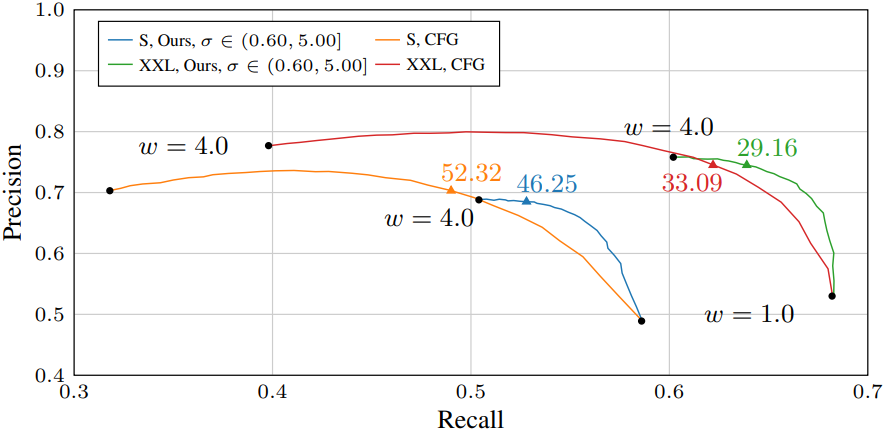
다음은 guidance 가중치에 따른 precision/recall을 비교한 결과이다.


다음은 guidance interval의 선택에 따른 FID를 비교한 결과이다.

3. Qualitative analysis

다음은 CFG와 생성된 샘플들을 비교한 결과이다.


다음은 다양한 guidance 가중치에 따라 생성된 샘플들을 비교한 결과이다.


다음은 다양한 guidance interval에 따라 생성된 샘플들을 비교한 결과이다.


다음은 guidance 가중치를 증가시켰을 때의 결과를 CFG와 비교한 것이다.

You may also enjoy