[논문리뷰] GSDF: 3DGS Meets SDF for Improved Rendering and Reconstruction

arXiv 2024. [Paper] [Page]
Mulin Yu, Tao Lu, Linning Xu, Lihan Jiang, Yuanbo Xiangli, Bo Dai
Shanghai Artificial Intelligence Laboratory | The Chinese University of Hong Kong | University of Science and Technology of China | Cornell University
25 Mar 2024

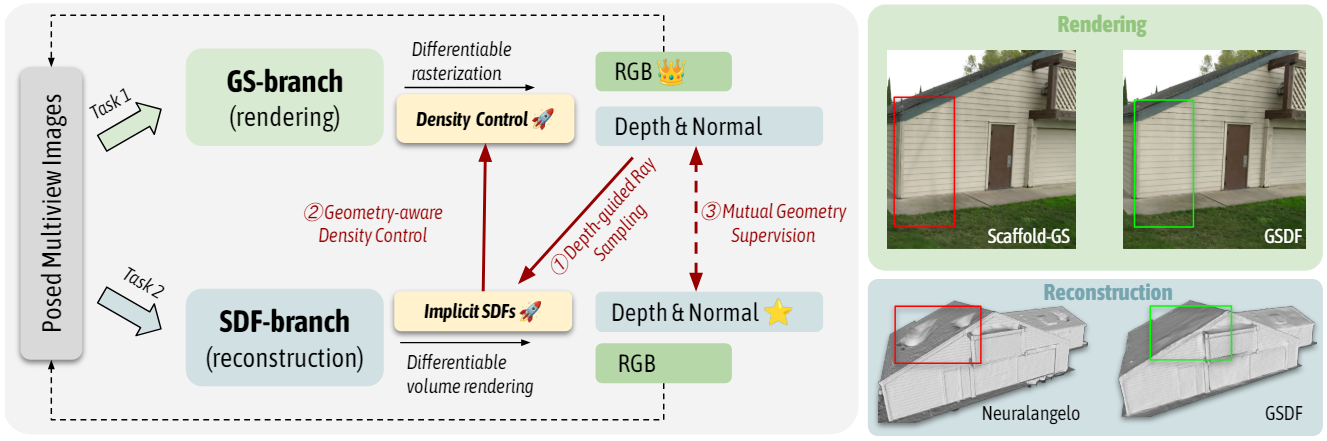
Introduction

뉴럴 표면 재구성 기술은 뉴럴 렌더링과 함께 우수성을 나타내지만 새로운 뷰 합성에만 초점을 맞춘 주요 방법에 비해 렌더링 충실도 저하로 인해 어려움을 겪는 경우가 많다. 복잡한 형상으로 장면을 확장하는 것도 여전히 어려운 과제로, 실제 적용이 제한된다. NeuSG, SuGaR와 같은 최근 접근 방식들은 표면 모델링을 위해 평면 Gaussian을 사용하였다. Gaussian 속성을 정규화하기 위해 바이너리 불투명도와 함께 학습된 NeuS 모델을 적용하는 동안 적용된 기본 제약 조건으로 인해 렌더링 품질이 저하되는 문제도 발생했다. 그럼에도 불구하고 Scaffold-GS와 같은 연구들에서는 geometry guidance가 실제로 잘 정규화된 공간 구조로 렌더링 품질을 향상시킬 수 있음을 보여주었다. 이러한 결과를 바탕으로 저자들은 동시에 최적화되는 이중 branch 시스템을 통해 두 접근 방식의 최적 혼합이 달성 가능하다는 가설을 세웠다. 광범위한 실험을 통해 신중하게 조정된 학습 supervision 및 최적화 전략을 통해 두 접근 방식은 뉴럴 렌더링이나 재구성의 우수성에 기여하는 본질적인 특성을 방해하지 않고 효율적인 상호 안내 및 supervision을 통해 보존될 수 있다.

본 논문에서는 렌더링을 위한 GS-branch와 표면 재구성을 위한 SDF-branch를 통합하였다. SDF-branch의 geometry prior와 함께 3DGS의 대략적인 형상 및 효율적인 rasterization을 위한 빠른 학습과 같은 양측의 강점을 모두 사용한다.

1. GS-branch에서 빠르게 rasterize된 깊이를 활용하여 SDF-branch의 광선 샘플링을 통해 볼륨 렌더링의 효율성을 높이고 local minima를 방지한다.
2. 3D-GS의 밀도 제어를 위해 SDF guidance를 사용하여 표면 근처 영역에서 3D Gaussian의 성장을 가이드하거나 제거한다.
3. 두 branch 모두에서 추정된 기하학적 특성(깊이, normal)을 정렬시킨다.

이 통합 시스템은 렌더링 방법과 장면 표현 간의 차이로 인해 발생하는 각 측면의 한계를 극복한다. GS-branch는 표면에 밀접하게 분산된 구조화된 Gaussian들을 생성하여 floater를 줄이고 뷰 합성의 디테일과 가장자리를 개선한다. 또한 SDF-branch의 가속화된 수렴으로 인해 기하학적 정확도가 향상되고 표면 디테일이 향상된다.

Method

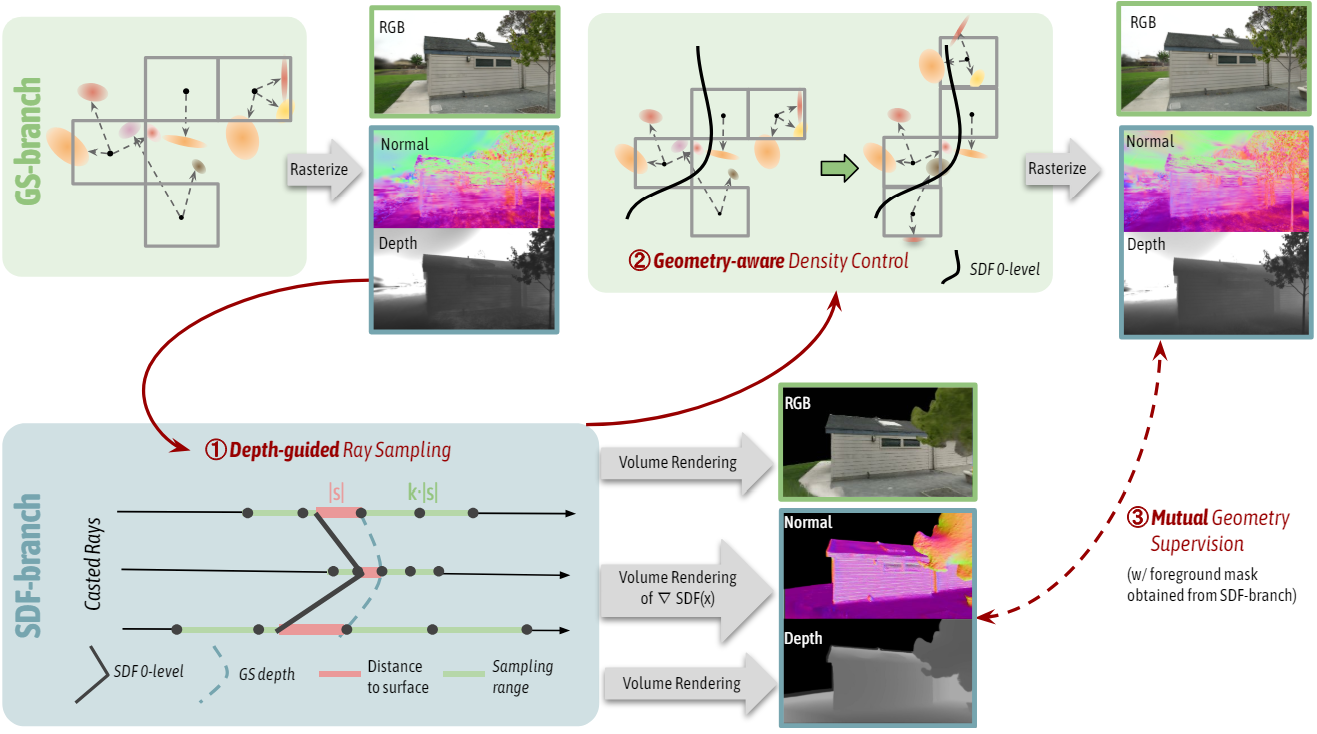
1. GSDF: Dual-branch for Rendering and Reconstruction

위 그림에서 볼 수 있듯이 이중 branch 설계에는 GS-branch와 SDF-branch가 통합되어 있다. 저자들은 효과성과 단순성을 위해 해시코딩을 backbone으로 적용한 Scaffold-GS와 NeuS를 선택했다.

GS $\rightarrow$ SDF: Depth Guided Ray Sampling

광선 샘플링 프로세스의 계산 비용을 해결하기 위해 계층적 샘플링, occupancy grid, early stopping, 소규모 proposal network와 같은 기술이 CUDA 가속과 함께 널리 채택되었다. 실제 센서 컬렉션이나 monocular estimation을 통해 입력 depth map을 사용할 수 있는 경우 샘플을 표면 영역 주위에 전략적으로 배치할 수 있다. SDF를 효과적으로 최적화하려면 포인트 샘플링 중 관심 구조에 대한 근접성(proximity)이 중요하다.

광선 샘플링을 가이드하기 위해 자체 예측된 SDF 값에 의존하는 기존 방법과 달리 GS-branch를 proximity로 사용하여 닭이 먼저냐 달걀이 먼저냐의 딜레마를 피한다. 대략적인 geometry guidance를 제공하기 위해 GS-branch에서 렌더링된 depth map을 활용하여 SDF-branch의 광선 샘플링 범위를 좁한다. 3D Gaussian들은 장면 형상 모델링에서 덜 정확하지만 효율성과 유연성이 뛰어나므로 많은 시간 오버헤드 없이 SDF-branch에 충분한 기하학적 단서를 제공한다.

$\textbf{v}$ 방향을 가리키는 카메라 중심 $\textbf{o}$에서 방출되는 광선에 대하여 GS-branch에서 렌더링되는 깊이 값 $D$는 다음과 같다.

\[\begin{equation} D = \sum_{i \in N} d_i \sigma_i \prod_{j=1}^{i-1} (1- \sigma_j) \end{equation}\]

여기서 $N$은 광선이 만나는 3D Gaussian 수를 나타내고, $\sigma_i$는 각 Gaussian의 불투명도, $d_i$는 $i$번째 3D Gaussian과 카메라 중심 사이의 거리를 나타낸다. SDF-branch를 최적화할 때 점들은 $\textbf{o} + D \cdot \textbf{v}$ 주위에서 샘플링된다. 모든 광선에 걸쳐 일정한 범위를 사용하는 대신 다양한 깊이에서 예측된 SDF 값 $s$를 기반으로 샘플링 범위를 조정한다.

\[\begin{equation} s = \mathcal{F}_\textrm{sdf} (\textbf{o} + D \cdot \textbf{v}) \end{equation}\]

여기서 \(\mathcal{F}_\textrm{sdf}\)는 주어진 공간적 위치에서 SDF 값을 예측하는 데 사용되는 SDF-branch의 2-layer MLP이다. 샘플링 범위는 다음과 같이 정의된다.

\[\begin{equation} r = [\textbf{o} + (D - k \vert s \vert) \cdot \textbf{v}, \textbf{o} + (D + k \vert s \vert) \cdot \textbf{v}] \end{equation}\]

저자들은 NeRF의 계층적 샘플링 전략에서 영감을 받아 각각 $k = 3$인 coarse한 샘플링 범위와 k = 1인 fine한 샘플링 범위를 정의하였다. 그런 다음 각 범위 내에서 광선을 따라 $M$개의 점을 균일하게 샘플링한다.

SDF $\rightarrow$ GS: Geometry-aware Gaussian Density Control

이전 방법들에서는 3D Gaussian들의 불투명도를 0과 1에 가깝게 flattening하여 3D-GS에서 장면 표면을 학습하려고 시도했으며, 3D Gaussian을 메쉬 삼각형과 유사한 표면들로 처리했다. 그 결과 이러한 제약으로 인해 렌더링 품질이 저하되고 표면이 불완전해질 수 있다. 본 논문에서는 Gaussian의 flattening을 권장하지 않지만 대신 형상 인식 밀도 제어 전략을 통해 3D Gaussian의 분포를 개선한다. 원래의 기울기 기반 밀도 제어 외에도 SDF-branch의 0-level set을 추가로 활용하여 Gaussian들이 표면에 가깝거나 표면에서 벗어나는지 여부를 식별한다. Gaussian의 위치로 SDF-branch를 쿼리하고 SDF 절댓값이 더 작은 Gaussian은 표면에 더 가까운 것으로 간주되며 SDF 절댓값이 크면 먼 것으로 간주된다.

Growing operator. 위치 $c$에 위치한 각 Gaussian에 대해 SDF-branch에서 SDF 값 $s = \mathcal{F}_\textrm{sdf} (c)$를 얻는다. Gaussian 성장의 기준은 다음과 같다.

\[\begin{equation} \epsilon_g = \nabla_g + \omega_g \mu (s) \\ \textrm{where} \quad \mu (s) = \exp (- \frac{s^2}{2\sigma^2}) \end{equation}\]

여기서 $\nabla_g$는 Scaffold-GS에서와 같이 $K$ iteration에 걸쳐 누적된 Gaussian의 평균 기울기이다. $\mu(s)$는 예측된 SDF 값을 양의 effecting factor로 변환하는 Gaussian function이다. 이 값은 0-level에서 벗어난 거리에 따라 단조 감소한다. 가중치 $\omega_g$는 geometry guidance의 중요성을 제어한다. $\epsilon_g > \tau_g$이면 존재하지 않는 경우 새로운 Gaussian이 추가된다.

Pruning operator. 마찬가지로, 원래의 불투명도 기반 제거 기준에 더해 표면에서 멀리 떨어져 있는 Gaussian(큰 SDF 값)을 추가로 제거한다. 제거 기준은 다음과 같다.

\[\begin{equation} \epsilon_p = \sigma_a - \omega_p (1 - \mu (s)) \end{equation}\]

여기서 $\sigma_a$는 K iteration에 대해 집계된 Gaussian의 불투명도 값이다. 가중치 $\omega_p$는 사용하여 투명성과 SDF 기여도의 균형을 맞춘다. $\epsilon_p < \tau_p$인 앵커는 제거된다.

GS $\leftrightarrow$ SDF: Mutual Geometry Supervision

렌더링 및 재구성 결과를 모두 향상시키기 위해 깊이와 normal을 중추적인 기하학적 특징으로 활용하여 이러한 상호 연결을 촉진하는 두 branch 간의 상호 supervision을 통합한다. 특히, SDF-branch의 경우 뷰별 depth map \(D_\textrm{sdf}\)는 볼류메트릭 렌더링 원리를 통해 렌더링되고, normal map \(N_\textrm{sdf}\)는 SDF 기울기의 볼류메트릭 렌더링을 통해 추론된다. GS-branch의 경우 $D$와 마찬가지러로 뷰별 depth map $D_\textrm{gs}$를 계산하고, 가장 작은 scaling factor의 방향을 각 Gaussian의 normal로 간주한다. 각 카메라 뷰에 대한 normal map을 렌더링하기 위해 알파 블렌딩을 사용하여 Gaussian들의 normal을 누적한다.

\[\begin{equation} N_\textrm{gs} = \sum_{i \in N} n_i \sigma_i \prod_{j=1}^{i-1} (1 - \sigma_j) \end{equation}\]

여기서 $n_i$는 $i$번째 Gaussian의 추정된 normal이다.

2. Training Strategy and Loss Design

GS-branch는 렌더링된 RGB 이미지와 ground truth 사이의 렌더링 loss \(\mathcal{L}_1\)과 \(\mathcal{L}_\textrm{SSIM}\)을 통해 supervise된다. Scaffold-GS를 따라 볼륨 정규화 항 \(\mathcal{L}_\textrm{vol}\)이 추가된다. GS branch의 전체 loss function은 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L}_\textrm{gs} = \lambda_1 \mathcal{L}_1 + (1 - \lambda_1) \mathcal{L}_\textrm{SSIM} + \lambda_\textrm{vol} \mathcal{L}_\textrm{vol} \end{equation}\]

SDF-branch는 렌더링 loss \(\mathcal{L}_1\), Eikonal loss \(\mathcal{L}_\textrm{eik}\), 곡률 불일치 \(\mathcal{L}_\textrm{curv}\)에 의해 supervise된다.

\[\begin{equation} \mathcal{L}_\textrm{sdf} = \mathcal{L}_1 + \lambda_\textrm{eik} \mathcal{L}_\textrm{eik} + \lambda_\textrm{curv} \mathcal{L}_\textrm{curv} \end{equation}\]

\(\mathcal{L}_\textrm{eik}\)은 예측된 SDF field의 기울기가 정규화되도록 보장한다. \(\mathcal{L}_\textrm{curv}\)는 Neuralangelo와 같은 일반적인 관행에 따라 표면 매끄러움을 촉진하는 곡률 loss이다.

상호 geometry supervision은 두 branch에 적용되는 깊이 및 normal 일관성 loss로 구성되며 다음과 같다.

\[\begin{aligned} \mathcal{L}_\textrm{mutual} &= \lambda_d \mathcal{L}_d + \lambda_n \mathcal{L}_n \\ &= \lambda_d \| D_\textrm{gs} - D_\textrm{sdf} \| + \lambda_n \bigg( 1 - \frac{\vert N_\textrm{gs} \cdot N_\textrm{sdf} \vert}{\| N_\textrm{gs} \| \times \| N_\textrm{sdf} \|} \bigg) \end{aligned}\]

여기서 \(\mathcal{L}_d\)와 \(\mathcal{L}_n\)은 두 branch 사이의 깊이와 normal 불일치이다.

공동 학습의 총 loss는 다음과 같이 정의된다.

\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{gs} + \mathcal{L}_\textrm{sdf} + \mathcal{L}_\textrm{mutual} \end{equation}\]

Experiment

• 데이터셋: Mip-NeRF360, DeepBlending, Tanks&Temples
• 구현 디테일
  • 해시그리드 해상도는 $2^5$에서 $2^{11}$로 확장 (16 level)
  • 각 해시 엔트리는 feature 차원이 4이고 각 level의 해시 엔트리 수는 $2^{21}$
  • 처음에는 8개의 해시 해상도를 사용하고 2,000 iteration 마다 level이 추가됨
  • 먼저 GS-branch를 15,000 iteration 동안 학습한 후 30,000 iteration 동안 두 branch를 공동 학습
  • 안정적인 최적화를 위해 처음 30,000 iteration 동안만 growing과 pruning을 적용

1. Results Analysis

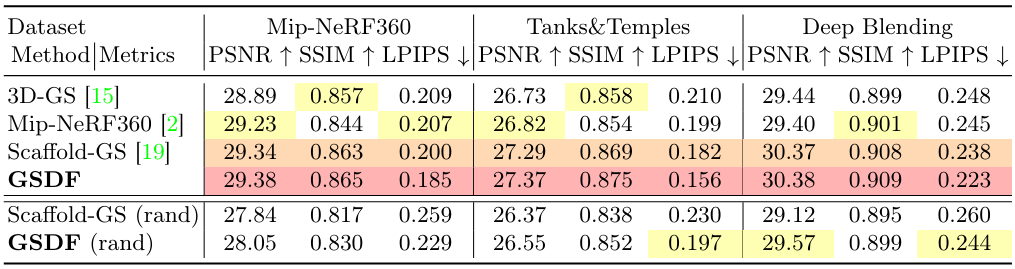
다음은 다른 방법들과 비교한 결과이다.

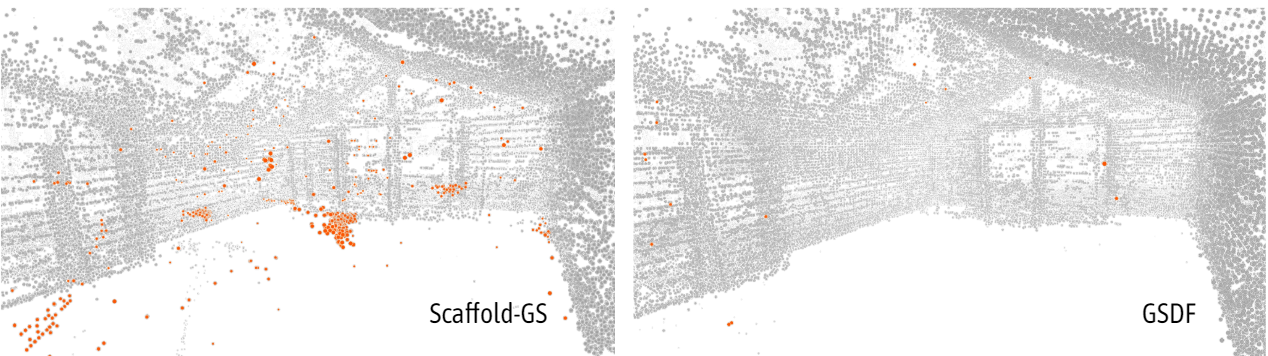
다음은 앵커 분포를 비교한 것이다.

다음은 메쉬 재구성 결과를 비교한 것이다.

2. Ablation Studies

다음은 GSDF의 각 구성 요소에 대한 ablation study 결과이다.

Limitations

많은 SDF 기반 재구성 방법과 마찬가지로 학습 속도는 빠른 rasterization을 사용하는 3D-GS만큼 효율적이지 않다. 결과적으로 SDF-branch를 포함하면 GS-branch의 학습 속도가 감소하며 이는 즉각적인 모델 학습이 필수적인 경우 단점이 될 수 있다. 더욱이 SDF는 투명/반투명 물체를 재구성하는 데 어려움을 겪고 있어 이러한 영역에서 geometry guidance의 효율성을 제한한다.