[논문리뷰] GS-ID: Illumination Decomposition on Gaussian Splatting via Adaptive Light Aggregation and Diffusion-Guided Material Priors

ICCV 2025. [Paper]
Kang Du, Zhihao Liang, Yulin Shen, Zeyu Wang
The Hong Kong University of Science and Technology | South China University of Technology | The Hong Kong University of Science and Technology
16 Aug 2024

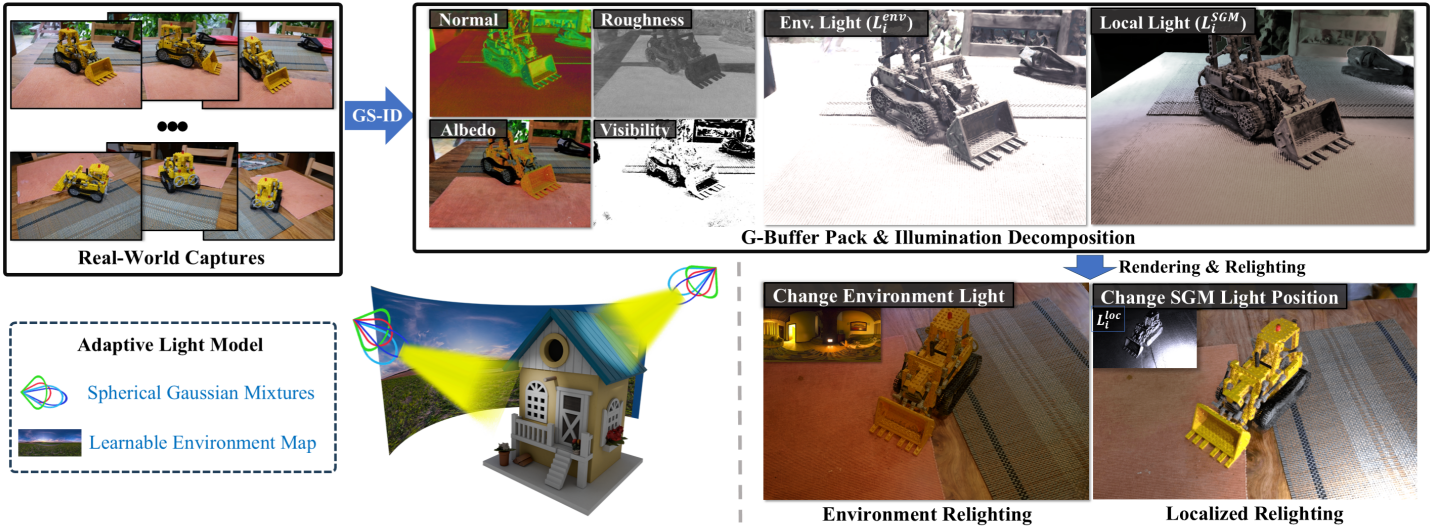
Introduction

3DGS에서 효과적인 조명 분해를 달성하는 데는 세 가지 중요한 과제가 있다.

1. 불충분한 조명 모델링: 기존 방법은 복잡한 조명 환경을 표현하는 데 어려움을 겪고 있으며, 종종 글로벌한 주변광과 로컬한 고주파 효과의 균형을 맞추지 못한다.
2. 분리되지 않은 그림자: 복잡한 조명과 geometry의 상호 작용으로 발생하는 그림자는 material 추정을 어렵게 만들고 분리하기 어렵다.
3. 잘못 설정된 intrinsic 추정: Prior가 없으면 3DGS의 결합된 출력을 geometry, material, 조명으로 분해하는 것이 매우 모호하다.

이러한 과제들을 해결하기 위해, 본 논문에서는 3DGS 기반 조명 분해를 위한 새로운 end-to-end 프레임워크인 GS-ID를 제안하였다. GS-ID는 적응형 조명 모델, deshadowing 모듈, 그리고 geometry와 material에 대한 사전 학습된 diffusion 기반 prior를 통합하였다. Deferred rendering을 활용한 맞춤형 CUDA 기반 최적화는 분해 프로세스를 더욱 가속화한다.

GS-ID는 학습 가능한 environment map을 통해 주변광을 표현하고, 공간적으로 변화하는 SGM을 사용하여 고주파 로컬 조명을 모델링하였다. 이러한 SGM은 3D 그리드에서 초기화되고 최적화 과정에서 적응적으로 집계되어 복잡한 조명 효과를 포착한다. 그림자로 인한 material 추정 오류를 처리하기 위해, splat별 visibility 벡터를 학습하는 deshadowing 모듈을 도입하여 네트워크가 여러 개의 알려지지 않은 광원으로 인해 발생하는 그림자를 구분할 수 있도록 한다.

마지막으로, 조명과 material 결합 최적화의 모호성을 해결하기 위해 사전 학습된 diffusion prior를 도입하였다. Geometry의 경우, 재구성을 안정화하기 위해 normal prior를 통합하였다. Material의 경우, 사전 학습된 diffusion model의 albedo map과 roughness map을 사용하여 분해를 유도한다.

Method

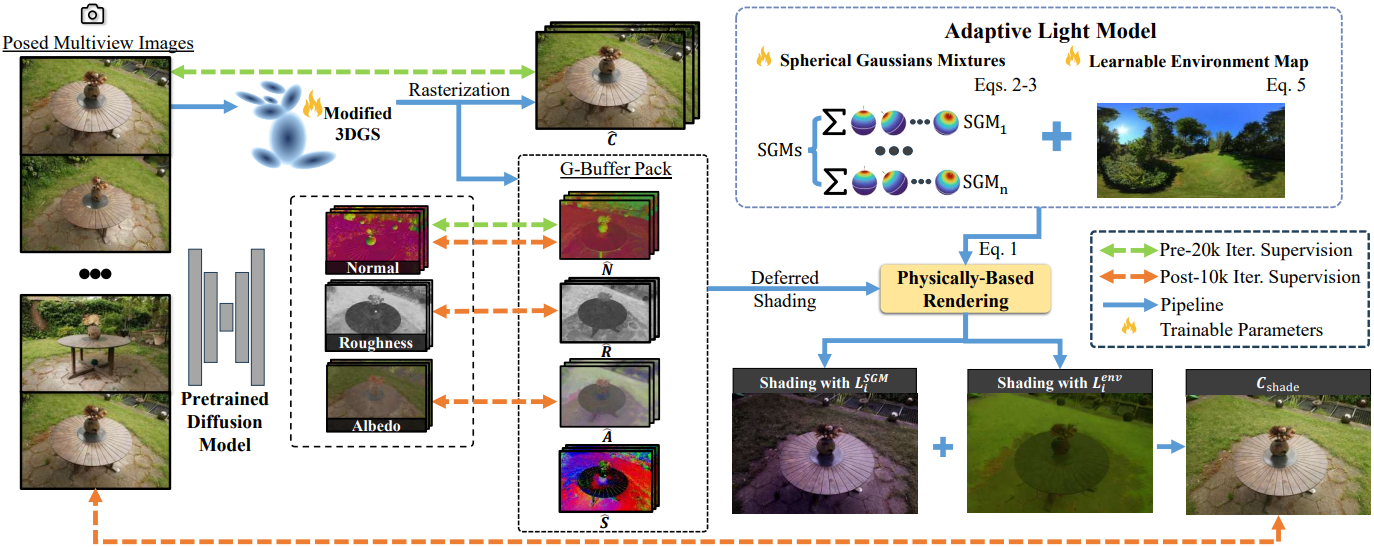
1. Adaptive Lighting Model

장면에서 복잡한 조명 조건을 효과적으로 모델링하는 것은 조명 분해를 위한 첫 단계이다. 본 논문에서는 로컬 emitter에서 발생하는 고주파 조명 성분을 모델링하기 위해 SGM 집합과 주변광을 모델링하기 위한 학습 가능한 environment map을 사용하는 적응형 조명 모델을 제안하였다. 초기 SGM은 $[-1, 1]^3$의 고정된 범위에 균일하게 배치된다. 본 논문에서는 이들을 통합하여 복잡한 로컬 조명을 적응적으로 모델링하는 최적화 프로세스를 수행한다.

이 적응형 조명 모델을 사용하여 들어오는 radiance를 다음과 같다.

\[\begin{equation} L_i = L_i^\textrm{SGM} + L_i^\textrm{env} \end{equation}\]

\(L_i^\textrm{SGM}\)는 여러 emitter에서 발생하는 고주파 효과를 나타내고, \(L_i^\textrm{env}\)는 멀리 떨어진 광원에서 발생하는 주변광이다. 렌더링 방정식은 다음과 같다.

\[\begin{aligned} L_o (x, \omega_o) &= \int_\Omega L_i^\textrm{env} (x, \omega_i) f_r (\omega_i, \omega_o) (\omega_i \cdot n) \textrm{d} \omega_i \\ &+ \int_\Omega L_i^\textrm{SGM} (x, \omega_i) f_r (\omega_i, \omega_o) (\omega_i \cdot n) \textrm{d} \omega_i \\ &\approx L_o^\textrm{env} (x, \omega_o) + L_o^\textrm{SGM} (x, \omega_o) \cdot V \end{aligned}\]

($x$는 3D 공간의 한 점, $n$은 표면 normal, $f_r$은 BRDF, \(\omega_i\)는 들어오는 빛의 방향, \(\omega_o\)는 나가는 빛의 방향, $V$는 그림자로 인한 변조 가중치)

SGM-Based Local Lighting

로컬 광원은 종종 하이라이트와 같은 다양한 조명 효과를 담당한다. 각 SGM이 $n_\textrm{SG}$의 개별 SG로 구성된 SGM을 사용하여 복잡한 로컬 조명을 모델링한다. SGM의 $k$번째 SG는 주 방출 방향 \(b_k \in \mathbb{S}^2\), 선명도 \(\lambda_k \in \mathbb{R}^{+}\), 진폭 \(\mu_k \in \mathbb{R}^{+}\), RGB 색도를 제어하는 혼합 가중치 \(w_k \in \mathbb{R}^3\)으로 parameterize된다. 여러 SGM을 3D 공간에 적응적으로 배치하고 집계하여 불규칙한 하이라이트를 유발하는 복잡한 광원을 모델링할 수 있다. SGM은 미분 가능한 파라미터로 인해 공동으로 최적화할 수 있다.

\[\begin{equation} \textrm{SGM}(\omega_o; b, \lambda, \mu) = \sum_{k=1}^{n_\textrm{SG}} \mu_k e^{\lambda_k (\omega_o \cdot b_k - 1)} \cdot w_k \end{equation}\]

표면 위의 $x$에서의 나가는 radiance $L_o^\textrm{SGM}$은 Cook-Torrance BRDF $f_r$을 통해 입사 조명을 통합한다.

\[\begin{aligned} L_o^\textrm{SGM} (x, \omega_o) &= \int_\Omega f_r (\omega_i, \omega_o) L_i^\textrm{SGM} (x, \omega_i) (n \cdot \omega_i) \textrm{d} \omega_i \\ &\approx \sum_j^{N_\textrm{light}} \frac{f_r^{(j)} \cdot \textrm{SGM} (\omega_o^{(j)}) (n \cdot \omega_i^{(j)}) \cdot V_j}{\vert p_j - \textbf{x} \vert^2} \end{aligned}\]

\(N_\textrm{light}\)개의 SGM은 3D 그리드에서 초기화되고 전략적으로 최적화된다. SGM 내의 모든 SG는 각각 SG 파라미터 \((b_k, \lambda_k, \mu_k)\)를 유지하면서 동일한 공간 위치 $p_j$를 사용한다. $\vert p_j - x \vert$는 표면과 $j$번째 광원 사이의 거리이며, 거리에 따른 조명 감쇠를 모델링한다. 계산 효율을 높이기 위해 $\vert w_k \vert < \tau$인 저에너지 SGM에 점진적 pruning을 적용한다.

\[\begin{equation} \tau^{(t)} = \max_{i,j,k} w_{ijk}^{(t)} + \ln(\delta) \end{equation}\]

SGM 최적화가 주변광이 아닌 로컬 조명의 정확한 모델로 이어지도록 하기 위해 각 SGM 광원의 위치와 값을 고려하는 두 가지 정규화 항을 도입하였다.

\[\begin{equation} \mathcal{L}_\textrm{pos} = \sum_j^{N_\textrm{light}} \max (d_\textrm{min}^{(j)} - d_\textrm{max}, 0), \quad \mathcal{L}_\textrm{val} \sum_j^{N_\textrm{light}} \sum_k^{n_\textrm{SG}} \| w_{jk} \|_2 \\ \mathcal{L}_\textrm{light} = \lambda_\textrm{pos} \mathcal{L}_\textrm{pos} + \lambda_\textrm{val} \mathcal{L}_\textrm{val} \end{equation}\]

여기서 \(d_\textrm{min}^{(j)} = \min_x \vert p_j - x \vert\)는 $j$번째 조명 위치 $p_j$와 표면 위치 $x$ 사이의 최소 거리를 나타낸다. 월드 좌표의 3D 위치 $x$는 depth buffer에서 깊이 값 $\hat{D}$를 back-projection하여 계산된다. \(d_\textrm{max}\)는 기본값이 3인 hyperparameter이다. 가중치 $w_{jk}$는 $j$번째 SGM에서 $k$번째 SG의 기여도를 제어하는 역할을 한다. 이 두 가지 정규화 항은 SGM이 표면을 향하도록 유도하여 SGM이 복잡한 로컬 조명을 더 잘 모델링할 수 있도록 한다.

본 논문의 SGM 기반 조명 모델은 적응형 메커니즘을 통해 공간적으로 변화하는 조명을 표현할 수 있다. 기존 방법들과 비교하여 본 논문의 접근법은 로컬한 하이라이트 영역과 같은 조명 효과를 생성하고 조명 편집을 쉽게 지원할 수 있다.

Ambient Lighting

로컬 조명 외에도, 주변광 \(L_o^\textrm{env}\)는 diffuse 성분 \(L_{o-\textrm{diff}}^\textrm{env}\)와 specular 성분 \(L_{o-\textrm{spec}}^\textrm{env}\)로 재구성될 수 있다. 적분을 처리하기 위해 이미지 기반 조명 모델과 split-sum approximation을 채택하였다. \(L_o^\textrm{env}\)는 다음과 같이 나타낼 수 있다.

\[\begin{equation} L_o^\textrm{env} (x, \omega_o) = L_{o-\textrm{diff}}^\textrm{env} + L_{o-\textrm{spec}}^\textrm{env}, \\ L_{o-\textrm{diff}}^\textrm{env} \approx K_\textrm{diff}^\textrm{env} L_\textrm{diff}^\textrm{env}, \quad K_\textrm{diff}^\textrm{env} = (1 - M) \frac{A}{\pi}, \\ L_{o-\textrm{spec}}^\textrm{env} \approx \underbrace{\int_\Omega \frac{DFG}{4(n \cdot \omega_o)} \textrm{d}l}_{\textrm{Environment BRDF} \; (K_\textrm{spec}^\textrm{env})} \cdot \underbrace{\int_\Omega D L_i (l) (l \cdot n) \textrm{d}l}_{\textrm{Pre-Fil. Env. Map} \; (I_\textrm{spec}^\textrm{env})} \end{equation}\]

\(K_\textrm{spec}^\textrm{env}\)은 미리 계산된 look-up table에서 빠르게 엑세스할 수 있다. \(I_\textrm{diff}^\textrm{env}\)와 \(I_\textrm{spec}^\textrm{env}\)는 학습 가능한 environment map에 내장되어 있다.

2. Deshadowing Model

재구성 과정에서 그림자가 albedo에 베이킹되어 부정확한 material 추정을 초래하는 경우가 많다. Ray tracing이나 오프라인 베이킹과 같은 기존 방법은 미분 불가능하고 계산 비용이 높아 확장성이 제한된다.

본 논문에서는 이 문제를 해결하기 위해 각 3D Gaussian에 여러 조명 아래에서 지배적인 그림자 방향을 포착하는 학습 가능한 단위 벡터 \(s \in \mathbb{S}^2\)를 할당하였다. 이 벡터들은 화면 공간 그림자 필드에 알파 블렌딩되어 G-buffer에 통합되므로 명시적인 ray tracing 없이도 효율적이고 미분 가능한 그림자 예측이 가능하다. 이러한 deshadowing 메커니즘은 학습 중에만 사용된다. Inference 단계에서는 표준 그림자 매핑 기법을 사용하여 relighting을 적용한다.

방향 \(\omega_i^{(j)}\)에서 입사되는 빛의 visibility는 다음과 같이 추정된다.

\[\begin{equation} V_j = \sigma (\alpha \cdot \hat{S} \cdot \omega_i^{(j)} + \beta) \end{equation}\]

($\hat{S}$는 G-buffer에서 $s$를 알파 블렌딩하여 도출된 그림자 벡터장, $\sigma (\cdot)$는 시그모이드, hyperparameter $α$와 $β$는 각각 그림자 효과의 선명도와 기준을 조절)

이 미분 가능한 공식은 학습 중 그림자와 material의 분리를 용이하게 한다.

3. Diffusion-Guided Priors

3DGS Reconstruction with Normal Priors

3DGS 재구성에서는 광택이 나는 영역을 홀로 잘못 해석하는 경우가 있음이 관찰된다. 이 문제를 해결하기 위해 monocular geometry 추정 모델의 prior를 통합하여 출력 geometry를 개선했다. 구체적으로, 사전 학습된 diffusion model RGB↔X를 활용하여 normal을 제공한다. Loss \(\mathcal{L}_\textrm{base}\)는 다음과 같이 정의된다.

\[\begin{aligned} \mathcal{L}_\textrm{base} &= \mathcal{L}_\textrm{color} + \lambda_n \mathcal{L}_n \\ \mathcal{L}_n &= \sum_{\hat{n} \subset \hat{N}} \unicode{x1D7D9} (1 - \hat{n}^\top n) \end{aligned}\]

(\(\mathcal{L}_\textrm{color}\)는 3DGS의 RGB loss, $n$은 pseudo-GT normal, $\hat{n}$은 렌더링된 normal)

저자들은 원거리 영역의 신뢰할 수 없는 prior를 피하기 위해 깊이 마스크 가중치 체계를 제안하였다. 깊이 값이 기본 threshold인 0.8을 초과하는 픽셀에는 가중치 0을 할당하고, 그렇지 않은 픽셀에는 가중치 1을 할당한다 (위 식에서 $\unicode{x1D7D9}$). Normal prior를 통합함으로써 normal 추정의 정확도를 높이고 텍스처가 없는 영역에서 geometry 재구성 문제를 해결하여 강력한 normal 추정을 제공한다.

Light Optimization with Material Priors

공동 조명 최적화의 내재적 모호성을 줄이기 위해 RGB↔X에서 얻을 수 있는 pseudo-GT material 속성을 활용한다.

\[\begin{equation} \mathcal{L}_\textrm{material} = \lambda_R L_2 (R, \hat{R}) + \lambda_A L_2 (A, \hat{A}) \end{equation}\]

($\hat{R}$과 $\hat{A}$는 렌더링된 roughness와 RGB albedo map, $R$과 $A$는 pseudo-GT roughness와 albedo map)

Metallic 항은 조명 효과에 미치는 영향이 미미하므로 생략되었다. 총 loss는 다음과 같다.

\[\begin{equation} \mathcal{L}_\textrm{total} = \mathcal{L}_\textrm{base} + \mathcal{L}_\textrm{light} + \mathcal{L}_\textrm{material} \end{equation}\]

초기 장면이 재구성된 후 10,000 iteration 이후에 \(\mathcal{L}_\textrm{light}\)와 \(\mathcal{L}_\textrm{material}\)이 적용된다.

Experiments

• 데이터셋: TensoIR Synthetic, Aria Digital Twin (ADT), Mip-NeRF 360
• 구현 디테일
  • \(\delta = 10^{-3}\)  
  • \(\lambda_\textrm{pos} = \lambda_\textrm{val} = 1 \times 10^{-6}\)  
  • $\alpha = 8$, $\beta = 10^{-3}$
  • \(\lambda_n = 0.05\), \(\lambda_R = 0.1\), \(\lambda_A = 1.0\)
  • \(n_\textrm{SG} = 16\)  
  • SGM은 해상도가 $M^3$인 grid에 위치 ($M = 3$)

\[\begin{equation} p_j = c_\textrm{min} + \left( \frac{j_x}{M-1}, \frac{j_y}{M-1}, \frac{j_z}{M-1} \right) \odot (c_\textrm{max} - c_\textrm{min}) \end{equation}\]

(\(c_\textrm{min}\)과 \(c_\textrm{max}\)는 AABB bound (default는 [-3, 3]), $j_x, j_y, j_z$는 grid 인덱스)

1. Comparative Analysis

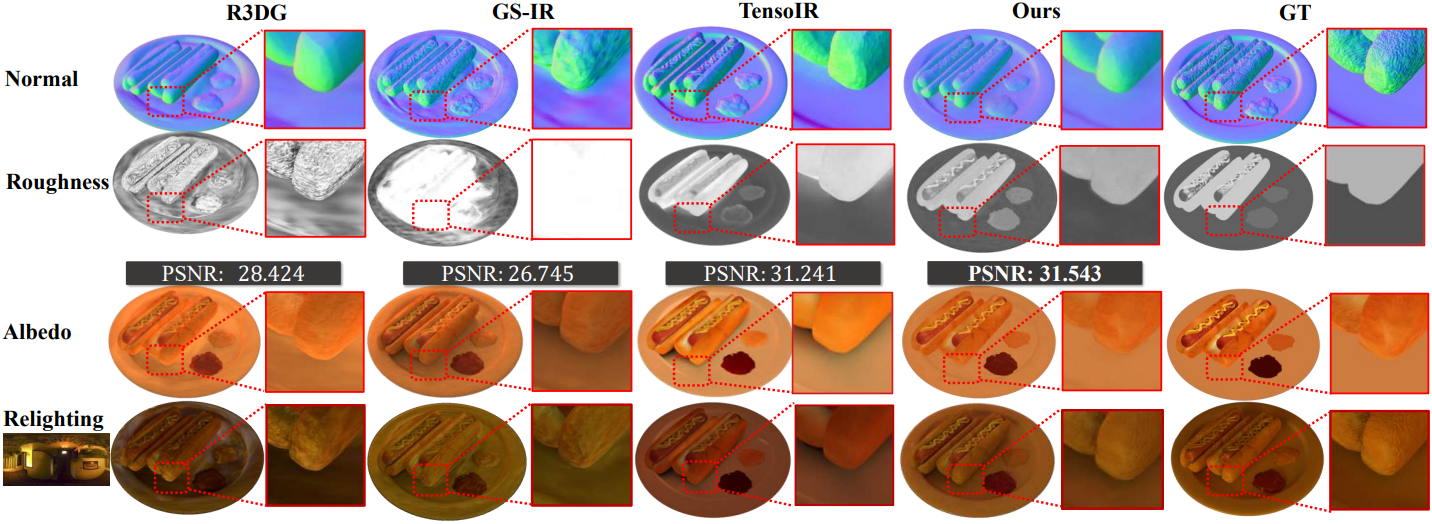
다음은 TensoIR Synthetic 데이터셋에서의 비교 결과이다.

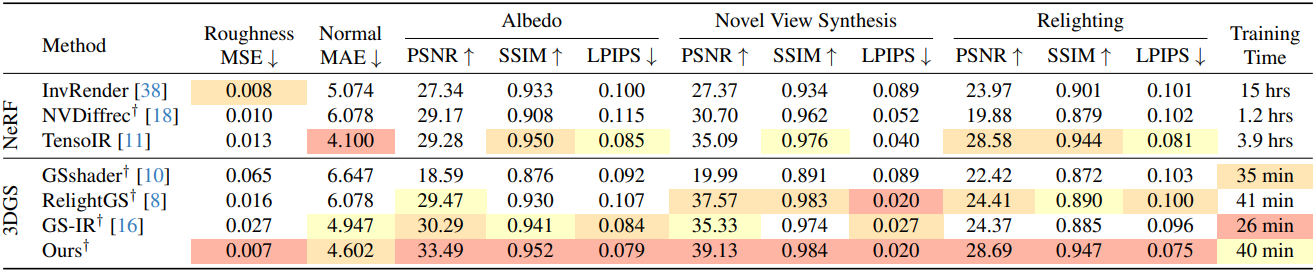
다음은 ADT 데이터셋에서의 비교 결과이다.

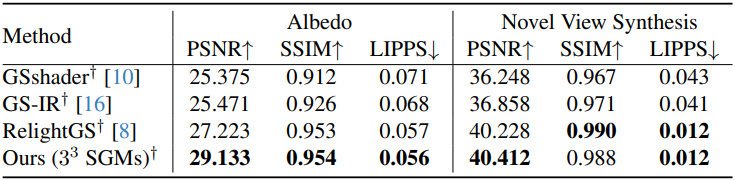
다음은 Mip-NeRF 360 데이터셋에서의 relighting 결과이다.

2. Ablation Study

다음은 ablation study 결과이다. (TensoIR)

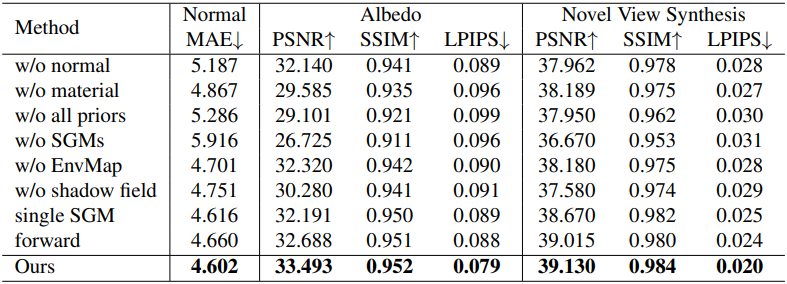
다음은 normal prior에 대한 효과를 나타낸 예시이다.

다음은 조명 성분에 대한 효과를 나타낸 예시이다.

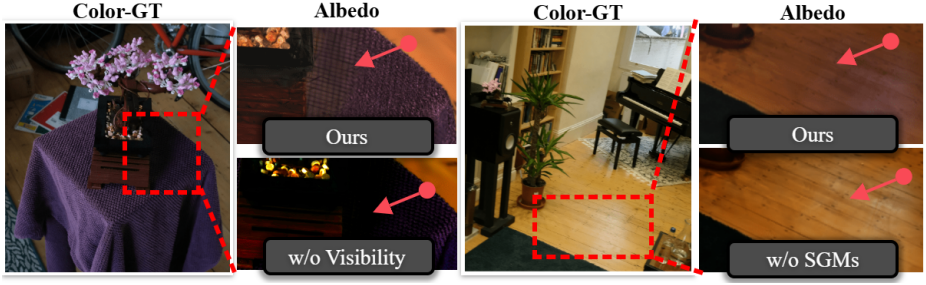
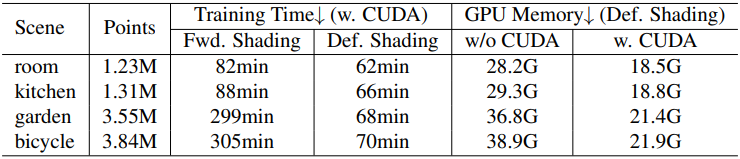
다음은 셰이딩 방식에 대한 비교 결과이다. (Mip-NeRF 360)