[논문리뷰] Learning to Simulate Complex Physics with Graph Networks (GNS)

ICML 2020. [Paper] [Github]
Alvaro Sanchez-Gonzalez, Jonathan Godwin, Tobias Pfaff, Rex Ying, Jure Leskovec, Peter W. Battaglia
DeepMind | Department of Computer Science, Stanford University
21 Feb 2020

Introduction

복잡한 물리학의 사실적인 시뮬레이터는 많은 과학 및 엔지니어링 분야에 매우 중요하지만 기존 시뮬레이터는 만들고 사용하는 데 비용이 많이 들 수 있다. 시뮬레이터 구축에는 수년간의 엔지니어링 노력이 수반될 수 있으며 종종 좁은 범위의 설정에서 정확성을 위해 일반성을 포기해야 한다. 고품질 시뮬레이터에는 상당한 계산 리소스가 필요하므로 확장이 불가능하다. 기본 물리학 및 파라미터에 대한 지식이 불충분하거나 근사화하기 어렵기 때문에 최고의 시뮬레이터라 할지라도 부정확한 경우가 많다. 기존 시뮬레이터에 대한 매력적인 대안은 머신 러닝을 사용하여 관찰된 데이터에서 직접 시뮬레이터를 학습시키는 것이지만, 표준 end-to-end 학습 접근 방식으로는 큰 state space와 복잡한 역학을 극복하기 어려웠다.

여기서 저자들은 Graph Network-based Simulators (GNS)라는 데이터로부터 복잡한 시스템을 시뮬레이션하는 방법을 배우기 위한 강력한 기계 학습 프레임워크를 제시한다. 본 논문의 프레임워크는 풍부한 물리적 state가 상호 작용하는 입자의 그래프로 표현되고 복잡한 역학이 node 간의 학습된 메시지 전달에 의해 근사화되는 강력한 inductive bias를 부과한다.

본 논문은 단일 딥 러닝 아키텍처에서 GNS 프레임워크를 구현했으며 유체, 단단한 고체, 변형 가능한 재료가 서로 상호 작용하는 광범위한 물리적 시스템을 정확하게 시뮬레이션하는 방법을 학습할 수 있음을 발견했다. 또한 본 논문의 모델은 학습된 것보다 훨씬 더 큰 시스템과 더 긴 시간 스케일로 잘 일반화되었다. 이전의 학습 시뮬레이션 접근 방식은 특정 task에 대해 고도로 전문화되었지만 단일 GNS 모델이 수십 번의 실험에서 잘 수행되었으며 일반적으로 Hyperparameter 선택에 강력했다. 저자들의 분석에 따르면 장거리 상호 작용을 계산하는 능력, 공간적 불변성에 대한 inductive bias, 긴 시뮬레이션 궤적에 대한 오류 누적을 완화하는 학습 절차 등 몇 가지 핵심 요소에 의해 성능이 결정되는 것으로 나타났다.

GNS Model Framework

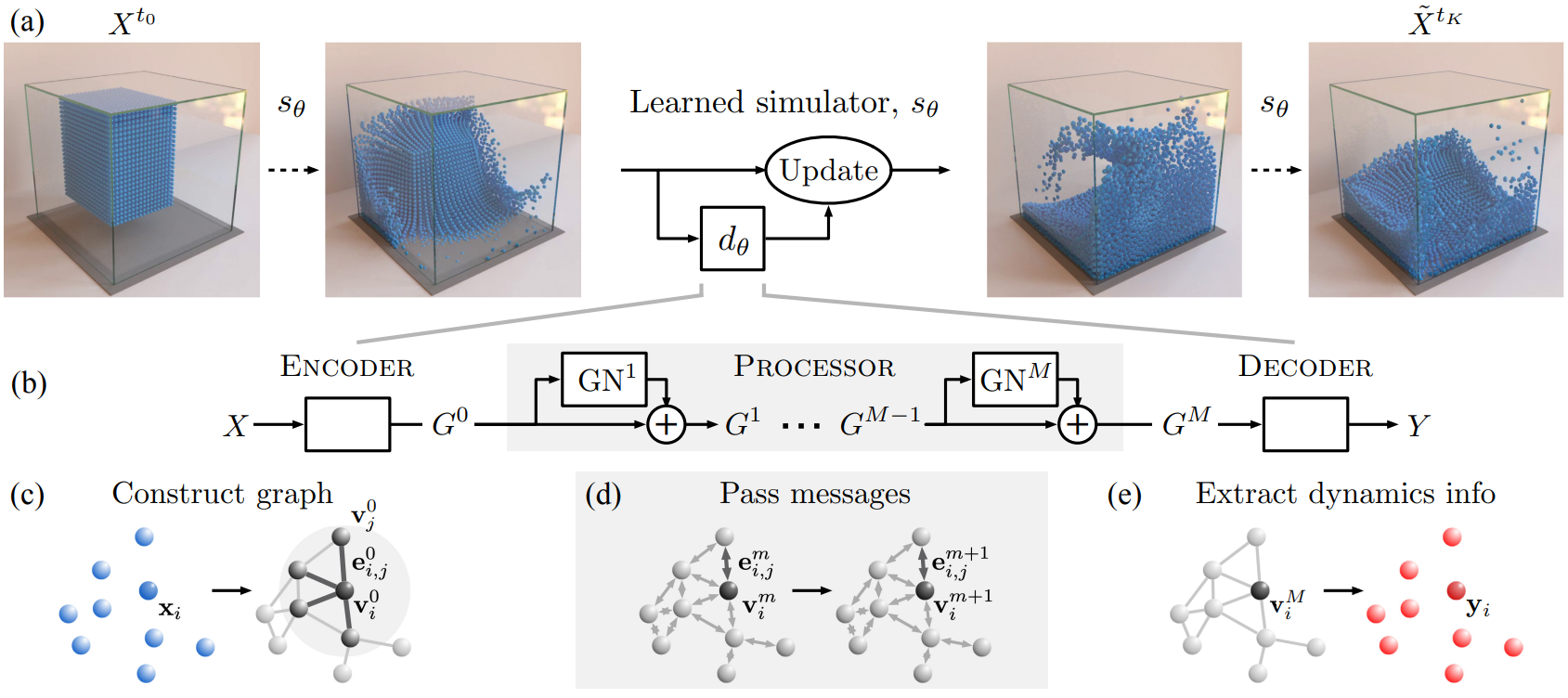
1. General Learnable Simulation

$X_t \in \mathcal{X}$가 시간 $t$에서의 world의 state라고 가정한다. $K$ timestep에 물리적 역학을 적용하면 state의 궤적 $X^{t_{0:K}} = (X^{t_0}, \cdots, X^{t_K})$가 생성된다. 시뮬레이터 $s : \mathcal{X} \rightarrow \mathcal{X}$는 이전 state를 인과적으로 이어지는 미래 state에 매핑하여 역학을 모델링한다. 시뮬레이션된 “rollout” 궤적을 $\tilde{X}^{t_{0:K}} = (X^{t_0}, \tilde{X}^{t_1}, \cdots, \tilde{X}^{t_K})$로 표시하고 $\tilde{X}^{t_{k+1}} = s (\tilde{X}^{t_k})$에 의해 각 timestep마다 반복적으로 계산된다. 시뮬레이터는 현재 state가 어떻게 변하고 있는지를 반영하는 역학 정보를 계산하고 이를 사용하여 현재 state를 예측된 미래 state로 업데이트한다. 예를 들어 수치적 미분 방정식 솔버가 있으며, 방정식은 역학 정보, 즉 시간 도함수를 계산하고 적분기가 업데이트 메커니즘이다.

학습 가능한 시뮬레이터 $s_\theta$는 parameterize된 function approximator $d_\theta : \mathcal{X} \rightarrow \mathcal{Y}$를 사용하여 역학 정보를 계산한다. 해당 파라미터 $\theta$는 일부 목적 함수에 대해 최적화될 수 있다. $Y \in \mathcal{Y}$는 업데이트 메커니즘에 의해 semantics가 결정되는 역학 정보를 나타낸다. 업데이트 메커니즘은 $\tilde{X}^{t_k}$를 취하고 $d_\theta$를 사용하여 다음 state인 $\tilde{X}^{t_{k+1}} = \textrm{Update} (\tilde{X}^{t_k}, d_\theta)$를 예측하는 함수로 볼 수 있다. 여기서는 간단한 업데이트 메커니즘(Euler integrator)과 가속도를 나타내는 $\mathcal{Y}$를 가정한다. 그러나 고차 적분기와 같이 $d_\theta$를 두 번 이상 호출하는 보다 정교한 업데이트 절차도 사용할 수 있다.

2. Simulation as Message-Passing on a Graph

본 논문의 학습 가능한 시뮬레이션 접근 방식은 물리적 시스템의 입자 기반 표현, 즉 $X = (x_0, \cdots, x_N)$을 사용하며, 각 $N$ 개의 입자의 $x_i$는 해당 state를 나타낸다. 물리적 역학은 이웃 간의 에너지 및 운동량 교환과 같은 입자 간의 상호 작용에 의해 근사화된다. 입자-입자 상호 작용이 모델링되는 방식은 시뮬레이션 방법의 품질과 일반성을 결정한다. 즉, 시뮬레이션할 수 있는 효과 및 재료의 유형, 방법이 잘 수행되거나 제대로 수행되지 않는 시나리오 등이 있다. 원칙적으로 입자 역학으로 표현될 수 있는 모든 시스템의 역학을 학습할 수 있어야 하는 이러한 상호 작용을 학습하는 데 관심이 있다. 따라서 서로 다른 $\theta$ 값을 통해 $d_\theta$가 광범위한 입자-입자 상호 작용 함수에 걸쳐 있도록 하는 것이 중요하다.

입자 기반 시뮬레이션은 그래프에서 메시지 전달로 볼 수 있다. node는 입자에 해당하고 edge는 상호 작용이 계산되는 입자 간의 쌍별 관계에 해당한다. 이 프레임워크에서 SPH와 같은 방법을 이해할 수 있다. Node 간에 전달되는 메시지는 예를 들어 밀도 커널을 사용하여 압력을 평가하는 것에 해당할 수 있다.

입자 기반 시뮬레이터와 그래프의 메시지 전달 간의 대응 관계를 활용하여 GN을 기반으로 범용 $d_\theta$를 정의한다. $d_\theta$에는 Encoder, Processor, Decoder의 세 단계가 있다.

Encoder definition

$\textrm{Encoder}: \mathcal{X} \rightarrow \mathcal{G}$는 입자 기반 state 표현 $X$를 latent graph

\[\begin{equation} G^0 = \textrm{Encoder}(X) \end{equation}\]

로 임베딩한다. $G = (V, E, u)$이며 $v_i \in V$이고 $e_{i,j} \in E$이다. Node embedding $v_i = \epsilon^v (x_i)$는 입자 state의 학습된 함수이다. 일부 잠재적인 상호 작용이 있는 입자 node 사이에 경로를 생성하기 위해 directed edge가 추가되었다. Edge embedding $e_{i,j} = \epsilon^e (r_{i,j})$는 해당 입자 $r_{i,j}$의 쌍 속성 (ex. 위치 간 변위, 용수철 상수 등)의 학습된 함수이다. Graph-level embedding $u$는 중력 및 자기장과 같은 글로벌 속성을 나타낼 수 있다.

Processor definition

$\textrm{Processor}: \mathcal{G} \rightarrow \mathcal{G}$는 학습된 메시지 전달의 $M$ step을 통해 node 간의 상호 작용을 계산하여 일련의 업데이트된 잠재 그래프 $G = (G^1, \cdots, G^M)$을 생성하며,

\[\begin{equation} G^{m+1} = \textrm{GN}^{m+1}(G^m) \end{equation}\]

이다. 최종적으로 최종 그래프 $G^M = \textrm{Processor}(G^0)$를 return한다. 메시지 전달을 통해 정보를 전파하고 제약 조건을 준수할 수 있다. 필요한 메시지 전달 step의 수는 상호 작용의 복잡성에 따라 확장될 수 있다.

Decoder definition

$\textrm{Decoder}: \mathcal{G} \rightarrow \mathcal{Y}$는 최종 latent graph의 node들에서 역학 정보를 추출한다.

\[\begin{equation} y_i = \delta^v (v_i^M) \end{equation}\]

$\delta^v$ 학습은 업데이트 절차에 의미론적으로 의미를 부여하기 위해 $\mathcal{Y}$ 표현이 가속도와 같은 관련 역학 정보를 반영하도록 해야 한다.

Experimental Methods

1. Physical Domains

저자들은 세 가지 다양하고 복잡한 물리적 재료가 포함된 데이터 세트에서 GNS가 어떻게 시뮬레이션을 학습하는지 살펴보았다.

1. 물 (겨우 감쇠되는 유체)
2. 모래 (복잡한 마찰 거동을 가진 입상 물질)
3. goop (점성이 있고 소성 변형 가능한 재료)

이러한 재료들은 동작이 매우 다르며 대부분의 시뮬레이터에서는 별도의 재료 모델 또는 완전히 다른 시뮬레이션 알고리즘을 구현해야 한다.

하나의 도메인에 대해 PBD 엔진 FleX를 사용하여 모두 입자로 표현되는 물이 담긴 용기와 내부에 떠 있는 입방체를 시뮬레이션하는 BOXBATH를 사용한다.

또한 저자들은 임의의 물 위치, 초기 속도 및 부피가 있는 고해상도 3D 물 시나리오인 WATER-3D를 만들었다. 엄격한 볼륨 보존 기능을 갖춘 SPH 기반 유체 시뮬레이터인 SPlisHSPlasH를 사용하여 이 데이터셋을 생성했다.

대부분의 도메인에서 Taichi-MPM 엔진을 사용하여 다양하고 까다로운 2D 및 3D 시나리오를 시뮬레이션한다. MPM은 매우 광범위한 재료를 시뮬레이션할 수 있고 PBD 및 SPH와 다른 속성(ex. 입자가 시간이 지남에 따라 압축될 수 있음)을 갖기 때문에 시뮬레이터용으로 MPM을 선택했다.

본 논문의 데이터셋에는 일반적으로 1000개의 train 궤적, 100개의 validation 궤적, 100개의 test 궤적이 포함되어 있으며, 각각은 300-2000 timestep (다양한 재료가 안정적인 평형 상태에 도달하기 위한 평균 지속 시간에 맞게 조정됨)에 대해 시뮬레이션되었다.

2. GNS Implementation Details

Input and output representations

각 입자의 입력 state 벡터는 위치, $C = 5$개의 이전 속도의 시퀀스 및 정적 재료 속성을 캡처하는 feature를 나타낸다.

\[\begin{equation} x_i^{t_k} = [p_i^{t_k}, \dot{p}_i^{t_k −C+1}, \cdots, \dot{p}_i^{t_k}, f_i] \end{equation}\]

시스템의 글로벌 속성 $g$에는 적용 가능한 경우 외력과 글로벌 재료 속성이 포함된다. 지도 학습의 예측 목표는 입자당 평균 가속도 $\ddot{p}_i$이다. 데이터셋에서는 $p_i$ 벡터만 필요하다. $\dot{p}_i$와 $\ddot{p}_i$는 유한 차분을 사용하여 $p_i$에서 계산된다.

Encoder details

$\textrm{Encoder}$는 각 입자에 node를 할당하고 입자의 로컬 상호 작용을 반영하고 동일한 해상도의 모든 시뮬레이션에 대해 일정하게 유지되는 “연결 반경” $R$ 내에서 입자 사이에 edge를 추가하여 그래프 구조 $G^0$를 구성한다. Rollout을 생성하기 위해 각 timestep에서 현재 입자 위치를 반영하기 위해 그래프의 edge가 nearest neighbor algorithm에 의해 다시 계산된다.

$\textrm{Encoder}$는 $\epsilon^v$와 $\epsilon^e$를 MLP로 구현하며, 각 node feature와 edge feature를 크기가 128인 latent vector $v_i$와 $e_{i,j}$로 인코딩한다.

저자들은 절대 위치 정보를 사용하는 $\textrm{Encoder}$와 상대 위치 정보를 사용하는 $\textrm{Encoder}$를 각각 테스트하였다. 절대 위치 정보를 사용하는 $\textrm{Encoder}$의 경우 $\epsilon^v$의 입력은 $x_i$에 글로벌한 feature를 concat한 것이다. $\epsilon^e$의 입력 $r_{i,j}$은 실제로 어떠한 정보도 가지고 있지 않으며 $G^0$의 $e_i^0$가 학습가능한 고정 bias 벡터로 설정된다.

상대 위치 정보를 사용하는 $\textrm{Encoder}$의 경우 절대적 공간 위치의 불변성에 대한 inductive bias를 포함하도록 디자인되었다. $\epsilon^v$는 $x_i$내의 $p_i$ 정보를 마스킹하여 무시하도록 강제된다. $\epsilon^e$는 상대적 위치 변위와 그 크기 $r_{i,j} = [(p_i - p_j), || p_i - p_j ||]$를 입력으로 받는다. 두 $\textrm{Encoder}$ 모두 각 $x_i$에 글로벌 속성 $g$를 concat한 뒤 $\epsilon^v$에 전달된다.

Processor details

본 논문의 프로세서는 동일한 구조를 가진 M개의 GN의 스택을 사용하며, 내부 edge 및 node 업데이트 함수는 MLP이고, 파라미터가 공유되거나 공유되지 않을 수 있다. 글로벌한 feature 또는 글로벌한 업데이트 (상호작용 네트워크와 유사) 없이 GN을 사용하고 입력 및 출력 latent node와 edge 속성 사이의 residual connection이 있다.

Decoder details

$\textrm{Decoder}$의 학습 함수 $\delta^v$는 MLP이다. $\textrm{Decoder}$ 후에 미래의 위치와 속도는 Euler integrator를 사용하여 업데이트되므로 $y_i$는 물리적 도메인에 따라 2D 또는 3D 차원의 가속도 $\ddot{p}_i$에 해당한다.

Neural network parameterizations

모든 NLP는 ReLU activation과 함께 2개의 hidden layer를 가지며 뒤에 non-linear activated output layer가 온다. 각 layer의 크기는 128이다. 출력 decoder를 제외한 모든 MLP는 학습 안정성을 개선하는 것으로 알려진 LayerNorm layer 뒤에 온다.

3. Training

Training noise

복잡하고 혼란스러운 시뮬레이션 시스템을 모델링하려면 모델이 긴 rollout에서 오차 누적을 완화해야 한다. Ground-truth one-step 데이터로 모델을 학습시키기 때문에 이러한 종류의 누적된 noise로 인해 손상된 입력 데이터가 표시되지 않는다. 이것은 noisy한 이전 예측을 입력으로 모델에 공급하여 rollout을 생성할 때 입력이 학습 분포 외부에 있다는 사실로 인해 더 많은 오차가 발생하여 더 많은 오차가 빠르게 누적될 수 있음을 의미한다. 저자들은 간단한 접근 방식을 사용하여 noisy한 입력에 대해 모델을 보다 견고하게 만든다. 학습 시 모델의 입력 속도를 random-walk noise $\mathcal{N} (0, \sigma v = 0.0003)$으로 모델의 입력 속도를 손상시키므로 학습 분포가 rollout 중에 생성된 분포에 더 가깝다.

Normalization

학습 중에 online으로 계산된 통계를 사용하여 모든 입력 및 대상 벡터를 요소별로 zero mean과 unit variance로 정규화한다. 예비 실험에 따르면 수렴된 성능이 눈에 띄게 향상되지는 않았지만 정규화가 더 빠른 학습으로 이어졌다고 한다.

Loss function and optimization procedures

학습 궤적에서 입자 state 쌍 $(x_i^{t_k}, x_i^{t_{k+1}})$을 랜덤하게 샘플링하고 타겟 가속도 $\ddot{p}_i^{t_k}$를 계산하고 예측된 입자당 가속도의 $L_2$ loss를 계산한다.

\[\begin{equation} L(x_i^{t_k}, x_i^{t_{k+1}}; \theta) = \| d_\theta (x_i^{t_k}) - \ddot{p}_i^{t_k} \|^2 \end{equation}\]

모델의 파라미터는 Adam optimizer로 최적화된다. $10^{-4}$에서 $10^{-6}$까지의 exponential learning rate decay를 사용하여 최대 2천만 기울기 업데이트 step을 수행한다. 모델은 훨씬 더 적은 step으로 학습될 수 있지만 공격적인 learning rate를 피하여 데이터셋 간 분산을 줄이고 설정 간 비교를 보다 공정하게 만든다.

Results

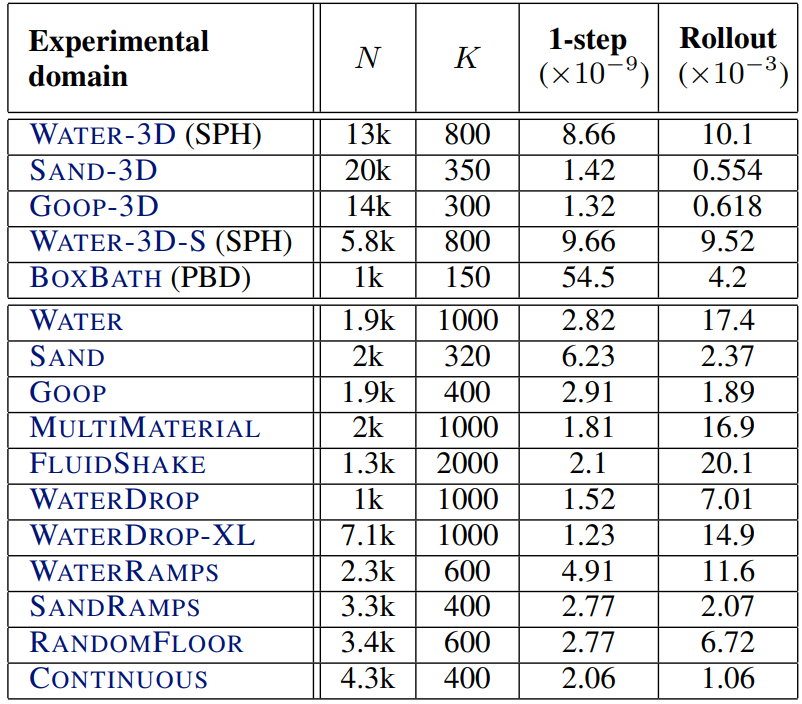
다음은 여러 실험 도메인에 대한 최대 입자 수 $N$, 시퀀스 길이 $K$, 모델 정확도 (MSE)를 나타낸 표이다.

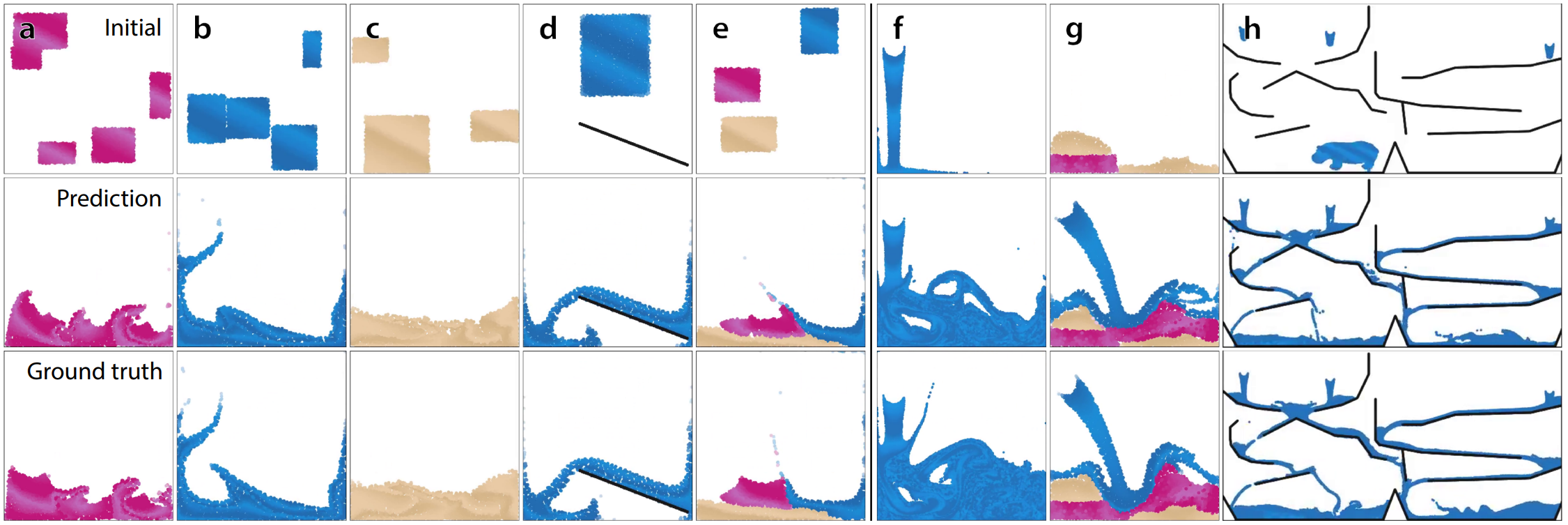
다음은 다양한 물질에 대한 시뮬레이션 결과이다. 아래 두 행은 각각 모델의 예측과 ground-truth의 마지막 프레임이다.

• (a): goop
• (b): 물
• (c): 모래
• (d): 다른 강체 장애물과의 상호작용 (WaterRamps)
• (e): 다양한 물질 사이의 상호작용 (MultiMaterial)
• (f): 고해상도 난기류 (WaterRamps로 학습)
• (g): 보지 못한 물체에 대한 상호작용 (MultiMaterial로 학습)
• (h): 상당히 더 넓은 도메인에 대한 일반화 (WaterRamps로 학습)

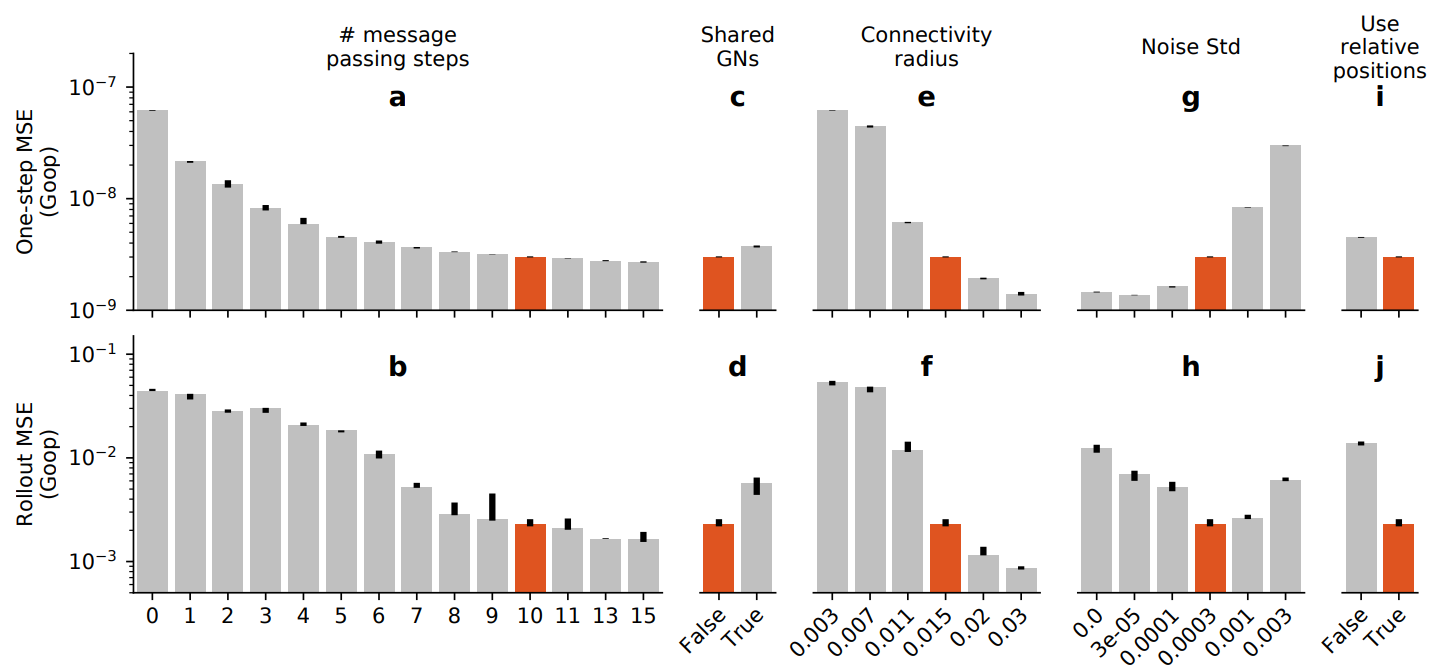
다음은 다양한 ablation의 효과를 나타낸 그래프로 본 논문의 모델은 빨간색으로 표시되었다.

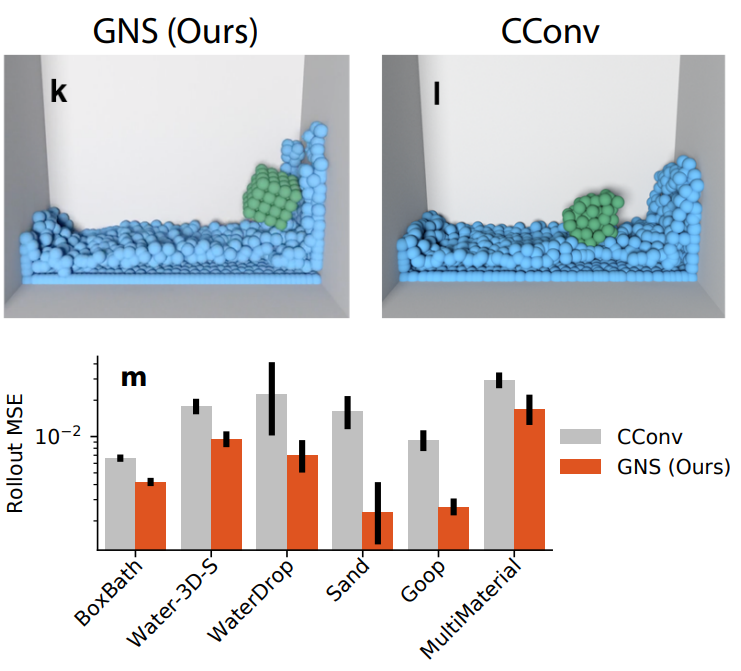
다음은 GNS 모델과 CConv의 평균 성능을 비교한 것이다.