[논문리뷰] Global Structure-from-Motion Revisited

ECCV 2024. [Paper] [Page] [Github]
Linfei Pan, Dániel Baráth, Marc Pollefeys, Johannes L. Schönberger
ETH Zurich | Microsoft
29 Jul 2024

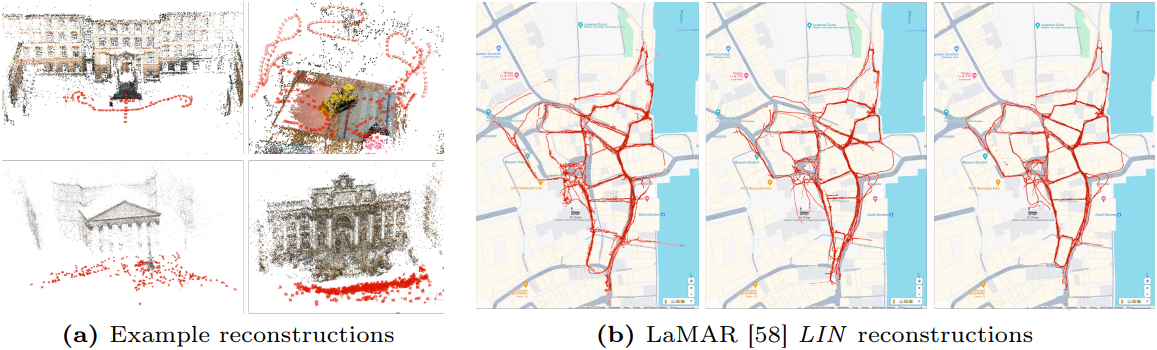
COLMAP의 후속 논문

Introduction

이미지 컬렉션에서 3D 구조와 카메라 모션을 복구하는 것을 일반적으로 Structure-from-Motion (SfM)이라 하며, 수년에 걸쳐 이를 해결하기 위한 두 가지 주요 패러다임, 즉 incremental SfM과 global SfM이 등장했다. 두 가지 모두 입력 이미지의 초기 뷰 그래프를 구성하기 위해 이미지 기반 feature 추출 및 매칭으로 시작하여 two-view geometry 추정이 이어진다. 그런 다음 incremental SfM은 두 뷰에서 재구성을 시작하여 추가 카메라 이미지와 관련 3D 구조를 순차적으로 확장한다. 이 순차적 프로세스는 카메라 포즈 추정, triangulation, bundle adjustment를 섞어서 높은 정확도와 견고성을 달성하지만, 비용이 많이 드는 반복적인 bundle adjustment로 인해 확장성이 제한된다.

대조적으로, global SfM은 뷰 그래프에서 모든 two-view geometry를 공동으로 고려하여 별도의 rotation averaging 단계와 translation averaging 단계에서 모든 입력 이미지에 대한 카메라 포즈를 한 번에 복구한다. 일반적으로 글로벌하게 추정된 카메라 포즈는 최종 global bundle adjustment 단계 전에 3D 구조의 triangulation을 위한 초기화로 사용된다.

SOTA incremental SfM은 더 정확하고 robust한 반면, global SfM의 재구성 프로세스는 더 확장 가능하고 실제로는 수십 배 더 빠르다. 본 논문에서는 global SfM의 문제점을 다시 살펴보고 SOTA incremental SfM과 유사한 수준의 정확도와 robustness를 달성하는 동시에 global SfM의 효율성과 확장성을 유지하는 포괄적인 시스템을 제안하였다.

Incremental SfM과 global SfM 사이의 정확도와 robustness 격차의 주된 이유는 global translation averaging 단계에 있다. Translation averaging은 이전에 rotation averaging으로 복구된 카메라 orientation으로 구성된 뷰 그래프의 relative pose 집합에서 글로벌한 카메라 위치를 추정한다. 이 프로세스는 실제로 세 가지 주요 과제에 직면한다.

스케일 모호성. 추정된 two-view geometry에서의 relative translation은 스케일까지만 결정될 수 있다. 따라서 글로벌한 카메라 위치를 정확하게 추정하려면 상대적 방향의 세 쌍이 필요하다. 그러나 이러한 세 쌍이 비뚤어진 삼각형을 형성할 때 추정된 스케일은 noise가 발생하기 쉽다.
상대적인 two-view geometry를 rotation과 translation으로 정확하게 분해하려면 정확한 카메라 intrinsic에 대한 사전 지식이 필요하다. 이 정보가 없으면 추정된 translation 방향에 큰 오차가 발생한다.
거의 co-linear인 모션에서 재구성 문제가 발생한다. 이러한 모션 패턴은 특히 순차적인 데이터셋에서 일반적이다. 이러한 문제는 카메라 위치 추정의 불안정성에 기여한다.

Translation averaging의 어려움으로 인해 이 문제에 대한 상당한 연구가 있었으며, 최근의 많은 접근 방식은 이미지 포인트들을 문제에 통합하기 때문에 incremental SfM과 공통적인 특성을 공유한다. 저자들은 이러한 통찰력을 바탕으로 global positioning 단계에서 카메라 위치와 3D 구조의 추정을 직접 결합하는 global SfM 시스템을 제안하였다.

본 논문은 GLOMAP이라는 범용 global SfM 시스템을 도입하였다. 이전 global SfM 시스템과의 핵심적인 차이점은 global positioning 단계에 있다. GLOMAP은 translation averaging을 먼저 수행한 다음 global triangulation을 수행하는 대신 카메라와 포인트 위치 추정을 공동으로 수행한다. GLOMAP은 global SfM 파이프라인의 효율성을 유지하면서 SOTA incremental SfM 시스템과 유사한 수준의 정확성과 robustness를 달성하였다. 대부분의 이전 global SfM 시스템과 달리, GLOMAP은 알려지지 않은 카메라 intrinsic을 처리할 수 있으며 순차적인 이미지 데이터를 robust하게 처리한다.

Global Structure-from-Motion

Global SfM 파이프라인은 일반적으로 세 가지 주요 단계로 구성된다.

Correspondence 검색
카메라 포즈 추정
카메라 및 포인트 공동 개선

1. Correspondence Search

Incremental SfM과 Global SfM은 모두 입력 이미지 $I = \{I_1, \ldots, I_N\}$에서의 이미지 feature 추출로 시작한다. 그 다음에는 이미지 쌍 $(I_i, I_j)$ 사이의 feature correspondence를 검색하는 과정이 이어진다. 매칭은 처음에 일반적으로 많은 outlier를 생성하지만 겹치는 쌍에 대한 two-view geometry를 robust하게 복구하여 검증한다. 계산된 two-view geometry는 global reconstruction 단계의 입력으로 사용되는 뷰 그래프 $G$를 정의한다.

본 논문에서는 RootSIFT feature와 bag-of-words 이미지 검색을 사용한 COLMAP의 correspondence 검색 구현에 의존한다.

2. Global Camera Pose Estimation

글로벌 카메라 포즈 추정은 global SfM과 incremental SfM을 구분하는 핵심 단계이다. 반복적인 triangulation과 bundle adjustment로 카메라 포즈를 순차적으로 추정하는 대신, global SfM은 뷰 그래프 $\mathcal{G}$를 입력으로 사용하여 모든 카메라 포즈 $\mathbf{P}_i = (\mathbf{R}_i, c_i) \in \mathbf{SE}(3)$을 한 번에 추정하려고 한다. 문제를 다루기 쉽게 만들기 위해 일반적으로 별도의 rotation averaging 단계와 translation averaging 단계로 분해하며, 일부 연구에서는 그 전에 뷰 그래프를 정제하기도 한다. 가장 큰 과제는 신중하게 모델링하고 최적화 문제를 풀어 뷰 그래프의 noise와 outlier를 처리하는 것이다.

Rotation Averaging

Rotation Averaging은 추정된 relative pose에서 global rotation의 편차에 페널티를 부여한다. 구체적으로, absolute rotation $\mathbf{R}_i$와 relative rotation $\mathbf{R}_{ij}$는 이상적으로 제약 조건 $\mathbf{R}_{ij} = R_j R_i^\top$를 충족해야 한다. 그러나 실제로는 noise와 outlier로 인해 이 조건이 정확히 성립하지 않는다. 따라서 일반적으로 robust한 least-metric objective로 모델링되며 다음과 같이 최적화된다.

\[\begin{equation} \underset{\mathbf{R}}{\arg \min} \sum_{i,j} \rho (d (\mathbf{R}_j^\top \mathbf{R}_{ij} \mathbf{R}_i, \mathbf{I})^p) \end{equation}\]

($\rho$: robustifier, $d$: distance metric)

본 논문에서는 Efficient and robust large-scale rotation averaging 논문의 방법을 확장 가능한 방식으로 구현하여 noise가 많고 outlier로 오염된 입력 rotation이 있는 경우에도 정확한 결과를 제공하는 방법을 사용했다.

Translation Averaging

Rotation averaging 후, 카메라 포즈에서 rotation $\mathbf{R}_i$를 얻을 수 있다. 결정해야 할 것은 카메라 위치 $\mathbf{c}_i$이다. Translation averaging은 제약 조건 $\mathbf{t}_{ij} = \frac{\mathbf{c}_j - \mathbf{c}_i}{\| \mathbf{c}_j - \mathbf{c}_i \|}$에 따라 쌍별 relative translation $\mathbf{t}_{ij}$와 최대로 일치하는 글로벌 카메라 위치를 추정한다. 그러나 noise와 outlier, relative translation의 스케일 모호성으로 인해 이 task는 특히 어렵다.

Translation averaging은 일반적으로 뷰 그래프가 잘 연결된 경우에만 안정적으로 작동한며, 카메라가 co-linear 모션에 근접할 때 noise에 민감하다. 또한, two-view geometry에서 relative translation을 추출하는 것은 카메라 intrinsic을 알고 있어야만 가능하다. 이러한 정보가 부정확하면 추출된 translation은 신뢰할 수 없다.

포인트 추적이 일반적으로 translation averaging에 도움이 된다는 관찰에서 영감을 받아 GLOMAP에서는 translation averaging 단계를 건너뛴다. 대신 카메라와 포인트 위치를 공동으로 직접 추정한다. 이 단계를 global positioning이라고 한다.

카메라를 복구한 후, triangulation을 통해 글로벌 3D 구조를 얻을 수 있다. 카메라 extrinsic 및 intrinsic과 함께 3D 구조는 일반적으로 global bundle adjustment를 사용하여 정제된다.

Global Triangulation

Two-view 매칭 쌍들이 주어지면 correspondence들의 transitivity를 활용하여 완전성과 정확성을 높일 수 있다. 본 논문에서는 공동 글로벌 최적화 방법을 통해 카메라 위치와 3D 포인트들을 직접 추정한다.

Global Bundle Adjustment

Global bundle adjustment는 정확한 최종 3D 구조 $\mathbf{X}_k \in \mathbb{R}^3$, 카메라 extrinsic $\mathbf{P}_i$, 카메라 intrinsic $\pi_i$를 얻는 데 필수적이다. Reprojection error를 최소화하여 공동으로 최적화한다.

\[\begin{equation} \underset{\pi, \mathbf{P}, \mathbf{X}}{\arg \min} \sum_{i,k} \rho (\| \pi_i (\mathbf{P}_i, \mathbf{X}_k) - x_{ik} \|_2) \end{equation}\]

Technical Contributions

1. Feature Track Construction

정확한 재구성을 위해 feature track을 신중하게 구성해야 한다. 먼저 two-view geometry 검증에서 생성된 inlier feature correspondence만 고려한다. Homography $\mathbf{H}$, essential matrix $\mathbf{E}$, fundamental matrix $F$ 중 two-view geometry를 가장 잘 설명하는 것을 inlier 검증에 사용한다. Cheirality test를 수행하여 outlier를 추가로 필터링한다. Epipole 중 하나에 가깝거나 triangulation 각도가 작은 correspondence도 큰 불확실성을 피하기 위해 제거된다. 모든 뷰 그래프 edge의 쌍별 필터링 후 나머지 모든 correspondence들을 연결하여 feature track을 형성한다.

2. Global Positioning of Cameras and Points

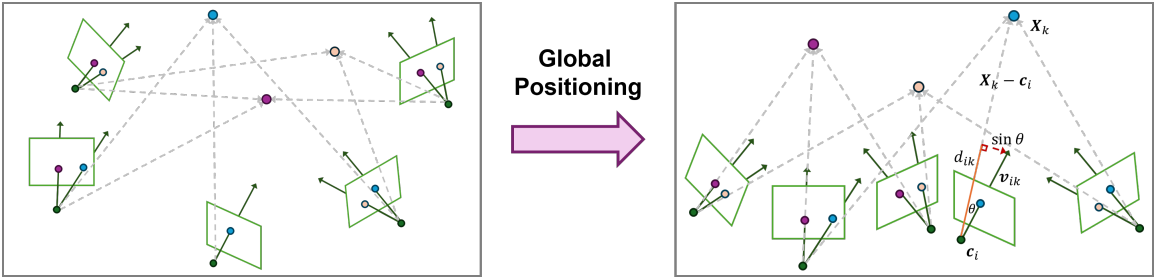
이 단계는 포인트와 카메라 위치를 공동으로 복구하는 것을 목표로 한다. Global triangulation을 하고 translation averaging을 수행하는 대신, global triangulation과 카메라 위치 추정을 직접 공동으로 수행한다.

기존 SfM 시스템에서 feature track은 reprojection error에 의해 검증되고 최적화되어 신뢰할 수 있고 정확한 triangulation이 보장된다. 그러나 여러 뷰에 걸친 reprojection error는 매우 non-convex하여 신중한 초기화가 필요하며, 오차에 제한이 없으므로 outlier에 강하지 않다.

이러한 과제를 극복하기 위해 Baseline Desensitizing In Translation Averaging 논문의 목적 함수를 기반으로 정규화된 방향 차이를 사용한다. 원래 공식은 relative translation 측면에서 제안되었지만, 본 논문에서는 relative translation 제약 조건을 무시하고 카메라 광선 제약 조건만 포함한다. 구체적으로, 다음과 같이 최적화된다.

\[\begin{equation} \underset{\mathbf{X}, \mathbf{c}, d}{\arg \min} = \sum_{i,k} \rho (\| \mathbf{v}_{ik} - d_{ik} (\mathbf{X}_k - \mathbf{c}_i) \|_2 ), \quad \textrm{subject to} \; d_{ik} \ge 0 \end{equation}\]

여기서 $\mathbf{v}_{ik}$는 카메라 $\mathbf{c}_i$에서 포인트 $\mathbf{X}_k$를 관찰하는 카메라 광선이고, $d_{ik}$는 normalizing factor이다. Robustifier $\rho$로 Huber loss를 사용하고, Ceres의 Levenberg–Marquardt를 optimizer로 사용한다. 모든 포인트와 카메라 변수는 $[-1, 1]$ 내의 균일한 랜덤 분포로 초기화되고, $d_{ik} = 1$로 초기화된다. 카메라 intrinsic을 모르는 경우 해당 카메라와 관련된 항의 가중치를 2배 낮추어 영향을 줄인다.

이 방법은 reprojection error와 비교하여 여러 가지 장점이 있다. 첫 번째는 robustness이다. $\theta$를 최적의 $d_{ik}$에 대한 $\mathbf{v}_{ik}$와 $\mathbf{X}_k - \mathbf{c}_i$ 사이의 각도라고 하면, 본 논문의 방법의 오차는

\[\begin{equation} \begin{cases} \sin \theta & \quad \textrm{if} \; \theta \in [0, \pi/2) \\ 1 & \quad \textrm{if} \; \theta \in [\pi/2, \pi] \end{cases} \end{equation}\]

와 동등하다. Reprojection error는 제한이 없지만, 이 오차는 $[0, 1]$에 엄격하게 제한된다. 따라서 outlier는 결과에 큰 편향을 주지 않는다. 둘째, 목적 함수는 bilinear 형태이기 때문에 랜덤하게 초기화해도 안정적으로 수렴한다.

고전적인 translation averaging과 비교했을 때 최적화 시 relative translation 항을 버리는 것은 두 가지 주요 이점이 있다.

부정확하거나 알려지지 않은 카메라 intrinsic과 pinhole 모델을 따르지 않는 카메라가 있는 데이터셋에 대하여 적용 가능해 진다.
쌍별 relative translation과 비교할 때, feature track은 여러 개의 겹치는 카메라를 제한한다. 따라서 일반적인 co-linear 모션 시나리오에서 더 안정적으로 처리할 수 있다.

3. Global Bundle Adjustment

Global positioning 단계는 카메라와 포인트에 대한 robust한 추정을 제공하지만, 특히 카메라 intrinsic을 모르는 경우 정확도가 제한된다. 추가 개선으로 Levenberg-Marquardt와 Huber loss를 사용하여 여러 라운드의 global bundle adjustment을 수행한다. 각 라운드 내에서 rotation을 먼저 고정한 다음 intrinsic과 포인트를 공동으로 최적화한다. 이러한 설계는 순차적 데이터를 재구성하는 데 특히 중요하다.

첫 번째 bundle adjustment 문제를 구성하기 전에 각도 오차를 기반으로 3D 포인트에 사전 필터링을 적용하며, calibration되지 않은 카메라에 대해 더 큰 오차를 허용한다. 그런 다음 이미지 공간의 reprojection error를 기반으로 track을 필터링한다. 필터링된 track의 비율이 0.1% 미만으로 떨어지면 반복이 중단된다.

4. Camera Clustering

인터넷에서 수집한 이미지의 경우 겹치지 않는 이미지가 잘못 매칭될 수 있으며, 결과적으로 서로 다른 재구성 결과가 하나로 붕괴된다. 이 문제를 해결하기 위해 카메라 클러스터링을 수행하여 재구성 결과를 후처리한다.

먼저, 각 이미지 쌍에 대해 보이는 포인트의 수를 세어 covisibility graph $\mathcal{G}$를 구성한다. 5개 미만의 카운트를 갖는 쌍은 relative pose를 신뢰할 수 없으므로 삭제하고 나머지 쌍의 median을 사용하여 inlier threshold $\tau$를 설정한다. 그런 다음 $\mathcal{G}$에서 강한 연결 요소 (strongly connected component)를 찾아 카메라의 클러스터를 찾는다. 강한 연결 요소는 $\tau$보다 많은 카운트를 갖는 쌍만 연결하여 정의한다. 그런 다음 $0.75 \tau$보다 많은 카운트를 갖는 edge가 두 개 이상 있는 경우 두 개의 강한 연결 요소를 병합한다. 더 이상 클러스터를 병합할 수 없을 때까지 이 절차를 재귀적으로 반복한다. 각 연결 요소는 별도의 재구성 결과로 출력된다.

5. Proposed Pipeline

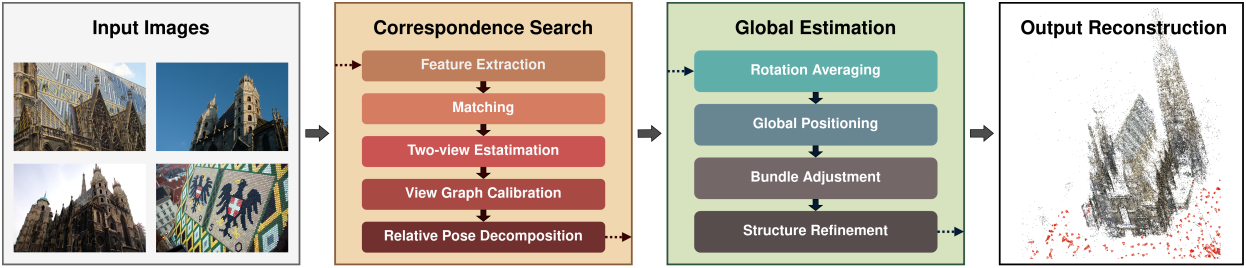
파이프라인은 위 그림에 요약되어 있으며, correspondence 검색과 글로벌 추정이라는 두 가지 주요 구성 요소로 구성된다.

Correspondence 검색의 경우 feature 추출 및 매칭으로 시작한다. Fundamental matrix, essential matrix, homography 포함한 two-view geometry는 매칭에서 추정된다. 기하학적으로 불가능한 매칭은 제외된다. 그런 다음 기하학적으로 검증된 이미지 쌍에 대해 view graph calibration을 수행한다. 업데이트된 카메라 intrinsic을 사용하여 relative pose를 추정한다.

글로벌 추정의 경우 rotation averaging을 통해 global rotation을 추정하고 $\mathbf{R}_{ij}$와 $\mathbf{R}_j \mathbf{R}_i^\top$사이의 각을 threshold로 설정하여 불일치하는 relative pose를 필터링한다. 그런 다음 global positioning을 통해 카메라와 포인트의 위치를 공동으로 추정한 다음 global bundle adjustment를 수행한다. 선택적으로 structure refinement를 통해 재구성의 정확도를 더욱 높일 수 있으며, 포인트는 추정된 카메라 포즈로 다시 triangulation되고 global bundle adjustment가 수행된다. 추가로 카메라 클러스터링을 사용하여 일관된 재구성을 달성할 수 있다.

Experiments

1. Calibrated Image Collections

ETH3D SLAM

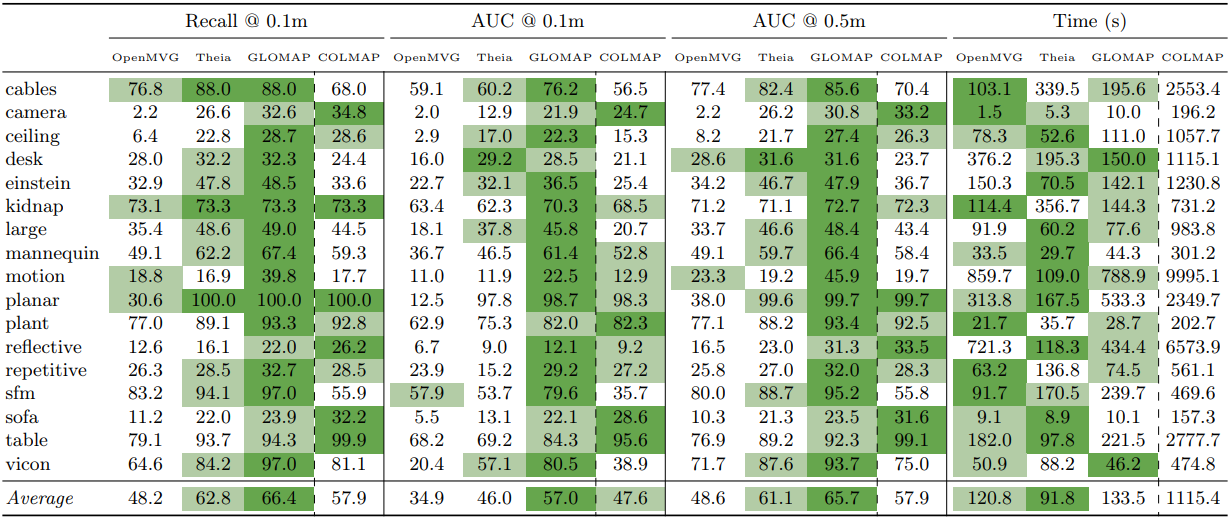
ETH3D MVS (rig)

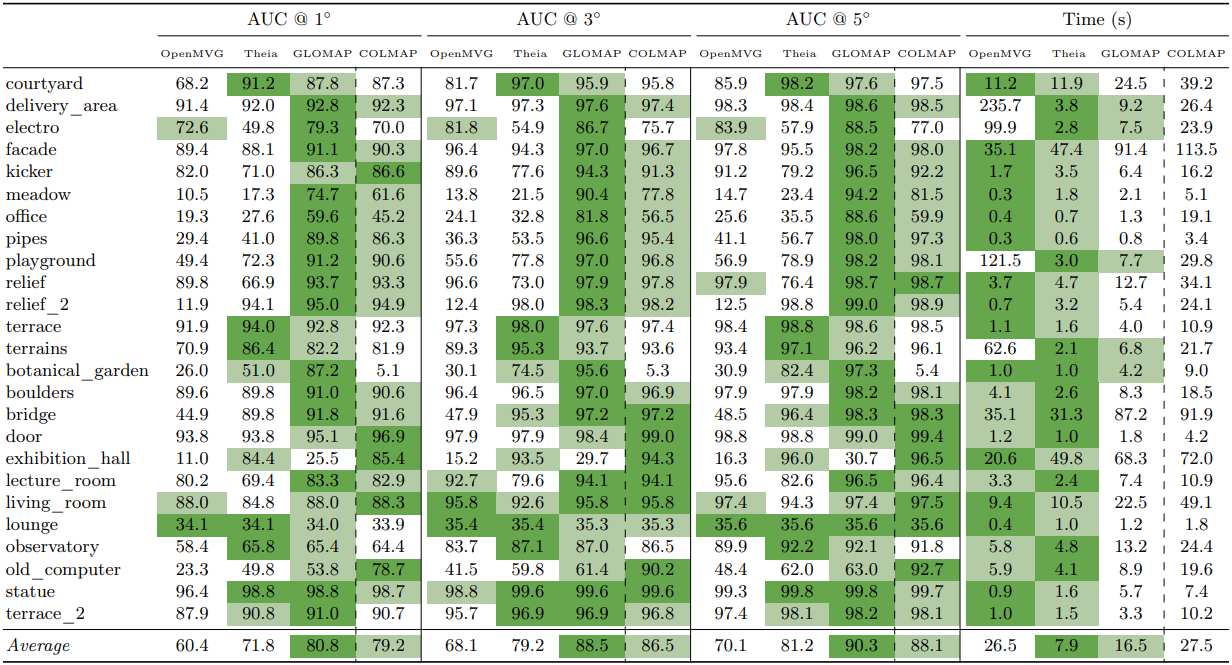
ETH3D MVS (DSLR)

LaMAR

2. Uncalibrated Images Collections

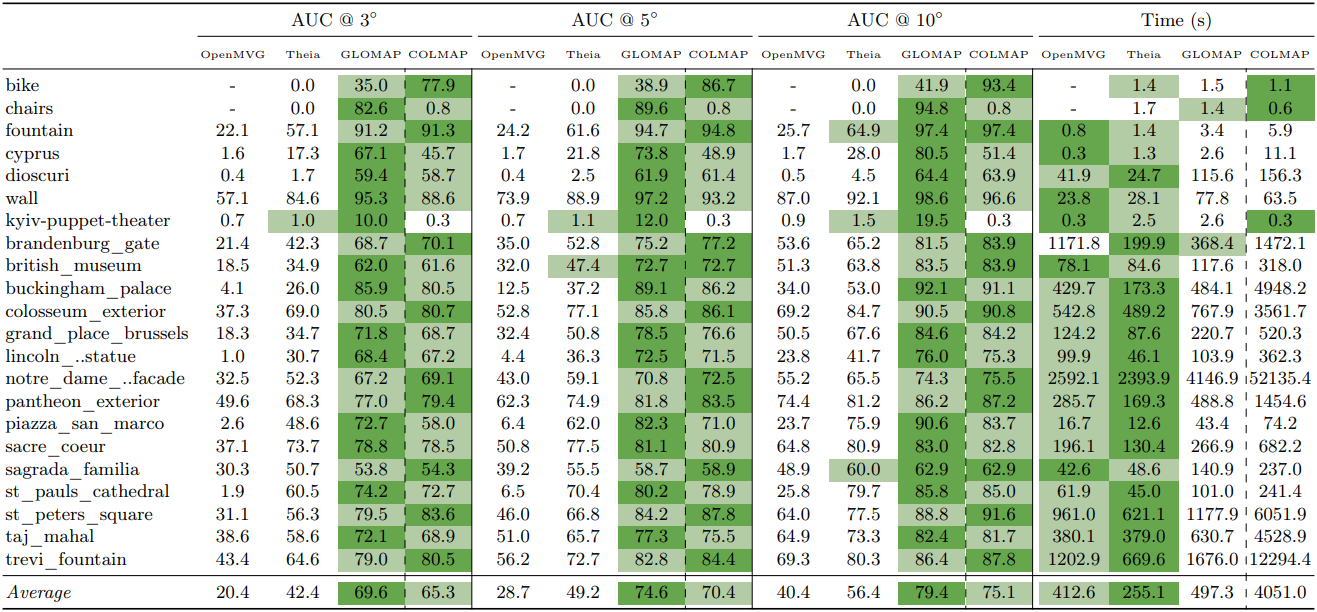
IMC 2023

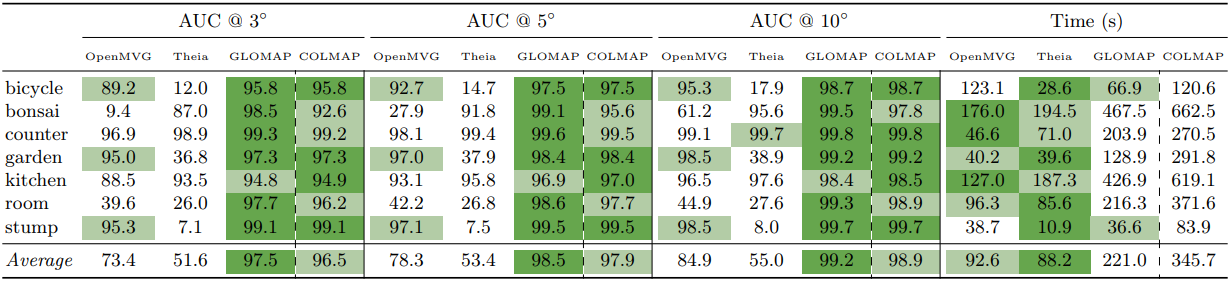
MIP360

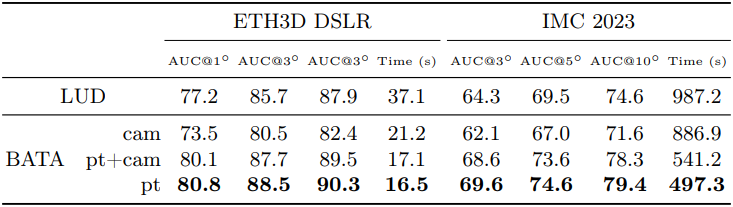
3. Ablation

Limitations

대칭 구조 등에 의해 rotation averaging이 실패하는 경우가 있다.
기존의 correspondence 검색에 의존하기 때문에 잘못 추정된 two-view geometry나 이미지 쌍을 완전히 매칭시킬 수 없는 경우 좋지 못한 결과로 이어진다.

JiYeop Kim