[논문리뷰] GeoSplatting: Towards Geometry Guided Gaussian Splatting for Physically-based Inverse Rendering
ICCV 2025. [Paper] [Page] [Github]
Kai Ye, Chong Gao, Guanbin Li, Wenzheng Chen, Baoquan Chen
Peking University | Sun Yat-sen University
31 Oct 2024
Introduction
3D Gaussian Splatting (3DGS)은 명확한 geometry 경계와 명확하게 정의된 표면 normal이 부족하여 light transport를 정확하게 모델링하지 못하고, 결과적으로 효과적인 material-조명 분리를 방해한다. 기존 방법은 geometry를 향상시키기 위해 3D Gaussian을 surfel로 압축하고, depth-normal regularization과 같은 implicit한 geometry 제약 조건을 통해 표면 normal을 근사하였다. 그럼에도 불구하고 light transport를 정확하게 모델링하려면 정확한 normal 방향과 불투명 표면이 모두 필요하며, 이는 각각 빛 전파 방향과 빛-표면 교차점을 정의한다. 결과적으로, 근사화된 normal과 Gaussian의 본질적으로 반투명한 특성에 의존하는 기존의 3DGS 기반 inverse Rendering 방법은 일반적으로 light transport 모델링에 어려움을 겪어 노이즈가 많은 material 분해와 잘못된 relighting으로 이어진다.
본 논문은 명시적인 geometry guidance를 통해 3DGS를 보완하는 GeoSplatting을 제안하였다. GeoSplatting은 implicit한 geometry 제약 조건에 의존하지 않고 최적화 가능한 명시적 메쉬로부터 표면에 정렬된 Gaussian들을 미분 가능하게 생성한다. 결과적으로, GeoSplatting은 명확하게 정의된 메쉬 normal과 불투명한 메쉬 표면을 활용하여 더욱 정확한 light transport 모델링을 구현하여, 뛰어난 material-조명 분리 및 향상된 relighting 품질을 제공한다.
특히, 저자들은 최적화 가능한 삼각형 메쉬를 geometry guidance로 활용하기 위해 isosurface 추출 기법을 통합했다. 메쉬 geometry를 기반으로 구조화된 Gaussian들을 미분 가능하게 구성하는 MGadapter를 도입함으로써, 명시적인 메쉬 normal과 불투명 메쉬 표면을 활용하여 정확한 light transport 모델링으로 3DGS를 향상시킬 수 있다. MGadapter의 완전 미분 가능 특성은 학습 과정에서 geometry guidance의 end-to-end 최적화를 가능하게 하여 메쉬와 3DGS 간의 일관성을 보장한다. 이러한 일관성은 효율적인 light transport 계산을 위한 메쉬 기반 ray tracing 기법의 사용을 더욱 용이하게 하며, 그림자 효과와 inter-reflection을 효과적으로 고려하는 동시에 탁월한 최적화 효율을 제공한다.
Method
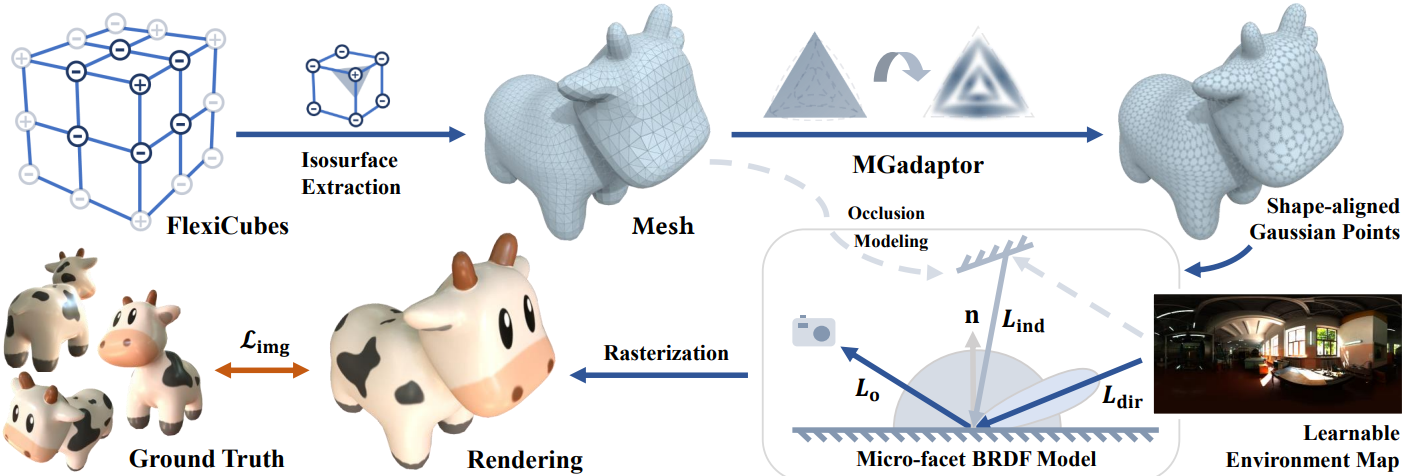
1. Geometry Guided Gaussian Points Generation
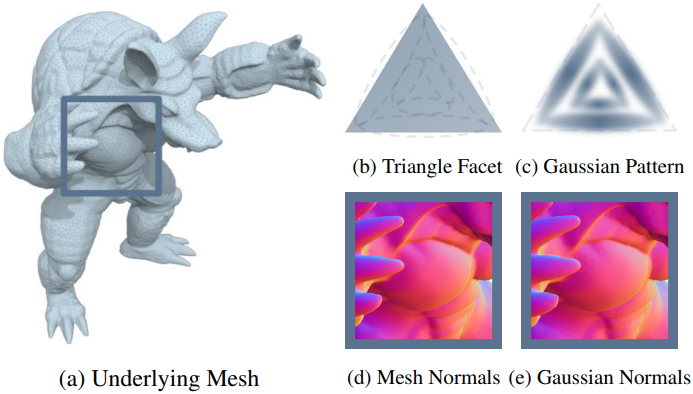
본 연구의 목표는 3D Gaussian Splatting에 명시적인 geometry guidance를 도입하는 것이다. 이를 위해 isosurface 테크닉인 FlexiCubes를 활용하고, 메쉬 geometry에 따라 가이드되는 Gaussian을 생성하는 MGadapter를 제안하였다. 공간적 위치를 스칼라 값으로 매핑하는 scalar field \(\zeta : \mathbb{R}^3 \rightarrow \mathbb{R}\)을 사용하여, isosurface는 $\zeta$를 grid vertex에 저장된 학습 가능한 값으로 discretize하여 표현할 수 있다. 그런 다음, 미분 가능한 isosurface 추출 기법인 FlexiCubes를 적용하여 $\zeta$로부터 삼각형 메쉬 $\textbf{M}$을 얻는다. MGadapter $\mathcal{T}$는 이 중간 메쉬 $\textbf{M}$을 명시적인 guidance로 사용하여, 각 삼각형 $\textbf{P}$에서 Gaussian 속성 \(\{(\boldsymbol{\mu}, \textbf{S}, \textbf{R}, \textbf{n})\}\)을 생성한다. 구체적으로, MGadapter는 각 삼각형 $\textbf{P}$에 대해 $K$개의 Gaussian을 생성한다.
(\(\boldsymbol{\mu}_i \in \mathbb{R}^3\)는 위치, \(\textbf{S}_i \in \mathbb{R}^3\)는 scale, \(\textbf{R}_i \in \mathbb{R}^{3 \times 3}\)는 rotation, \(\textbf{n}_i \in \mathbb{R}^3\)는 normal)
$\mathcal{T}$는 생성된 각 Gaussian의 모양 속성을 계산한다. Gaussian의 모양 파라미터는 각 삼각형 $\textbf{P}$에 의해 완전히 결정된다. 경험적으로 $K = 6$으로 설정하고 삼각형을 6개의 하위 영역으로 나누어 각 영역에 하나의 Gaussian을 배치한다. \(\boldsymbol{\mu}_i\)와 normal \(\textbf{n}_i\)는 barycentric interpolation을 통해 계산되고, \(\textbf{S}_i\)와 \(\textbf{R}_i\)는 삼각형 $\textbf{P}$의 방향과 모양에 의해 결정된다. 불투명도(opacity)는 1로 설정된다. 이 MGadapter 샘플링 프로세스는 완전히 미분 가능하므로 gradient가 isosurface $\zeta$로 효과적으로 전파될 수 있다.
근사화된 normal을 학습하고 normal-depth consistency loss를 사용하는 대신, 표면 기반 Gaussian은 잘 정의된 메쉬 normal을 활용하여 normal 정확도를 향상시킨다. 이는 근사화된 normal에 의존하는 기존 3DGS 기반 방식에 비해 inverse rendering 성능을 크게 향상시킨다. 또한, MGadapter는 삼각형 메쉬에 대한 geometry 일관성을 유지하는 고도로 구조화된 Gaussian들을 생성하도록 특별히 설계되었다. 이러한 geometry 정렬은 자연스럽게 중간 메쉬 $\textbf{M}$이 self-occlusion 평가를 할 수 있도록 하여 light transport 모델링을 용이하게 한다.
2. Physically-based Gaussian Rendering
본 논문의 목표는 PBR 속성을 Gaussian에 할당한 다음 렌더링 방정식을 평가하여 PBR 색상을 생성하는 것이다. 저자들은 PBR 속성 쿼리를 위해 multi-resolution hash grid \(\mathcal{E}_d\)와 \(\mathcal{E}_s\)를 도입하였다. 구체적으로, 위치가 \(\boldsymbol{\mu}_i\)인 Gaussian이 주어졌을 때, 해당 Gaussian의 PBR 속성은 다음과 같이 생성된다.
\[\begin{equation} \textbf{a}_i = \mathcal{E}_d (\boldsymbol{\mu}_i), \quad (\rho_i, m_i) = \mathcal{E}_s (\boldsymbol{\mu}_i) \end{equation}\]($\textbf{a} \in [0, 1]^3$은 albedo, $m_i \in [0, 1]$은 metallic, \(\rho_i \in [0, 1]\)은 roughness)
그런 다음, PBR 방정식을 통해 최종 이미지를 렌더링한다.
\[\begin{equation} \textbf{L}_o (\textbf{x}, \boldsymbol{\omega}_o) = \int_{\mathcal{H}^2} \textbf{f}_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) \textbf{L}_i (\textbf{x}, \boldsymbol{\omega}_i) \vert \textbf{n} \cdot \boldsymbol{\omega}_i \vert \textrm{d} \boldsymbol{\omega}_i \\ \textbf{f}_r (\textbf{x}, \boldsymbol{\omega}_i, \boldsymbol{\omega}_o) = (1-m) \frac{\textbf{a}}{\pi} + \frac{DFG}{4 \vert \textbf{n} \cdot \boldsymbol{\omega}_i \vert \vert \textbf{n} \cdot \boldsymbol{\omega}_o \vert} \end{equation}\]3. Light Transport Modeling
입사광 \(\textbf{L}_i (\textbf{x}, \boldsymbol{\omega}_i)\)를 정확하게 모델링하는 것은 여전히 어려운데, 이는 \(\textbf{L}_i (\textbf{x}, \boldsymbol{\omega}_i)\)가 환경 조명뿐만 아니라 inter-reflection에 의한 간접 조명까지 포함하기 때문이다. 그림자와 inter-reflection과 같은 효과를 포착하려면 효과적인 light transport 모델링이 필요하다. 기존 접근법은 1번 반사하는 모델로 조명을 근사하여 \(\textbf{L}_i (\textbf{x}, \boldsymbol{\omega}_i)\)를 두 가지 성분, 즉 환경 조명을 나타내는 직접 조명 항 \(\textbf{L}_\textrm{dir} (\boldsymbol{\omega})\)와 inter-reflection을 고려하는 간접 조명 항 \(\textbf{L}_\textrm{ind} (\textbf{x}, \boldsymbol{\omega}_i)\)로 분리한다. Self-occlusion을 모델링하기 위해 스칼라 \(O(\textbf{x}, \boldsymbol{\omega}_i)\)를 도입하여 이 두 조명 성분 간의 비율에 가중치를 부여한다.
\[\begin{equation} \textbf{L}_i (\textbf{x}, \boldsymbol{\omega}_i) = (1 - O (\textbf{x}, \boldsymbol{\omega}_i)) \textbf{L}_\textrm{dir} (\boldsymbol{\omega}_i) + O (\textbf{x}, \boldsymbol{\omega}_i) \textbf{L}_\textrm{ind} (\textbf{x}, \boldsymbol{\omega}_i) \end{equation}\]일반적으로 \(\textbf{L}_\textrm{dir} (\boldsymbol{\omega}_i)\)는 $H \times W \times 3$ environment map으로 표현되며, \(\textbf{L}_\textrm{ind} (\textbf{x}, \boldsymbol{\omega}_i)\)는 Spherical Harmonic (SH) 계수들로 표현된다.
본 논문의 목표는 효과적인 light transport 모델링을 달성하는 것이다. 이를 위한 핵심은 occlusion 항 \(O(\textbf{x}, \boldsymbol{\omega}_i)\)를 정확하고 효율적으로 추정하는 것이다. 기존의 3DGS 기반 inverse rendering 방식은 일반적으로 occlusion 항을 연속적인 값 \(O_\textrm{3dgs} (\textbf{x}, \boldsymbol{\omega}_i) \in [0, 1]\)로 모델링하고, 광선 $\textbf{r}(t) = \textbf{x} + t \boldsymbol{\omega}_i$$를 따라 Gaussian 불투명도를 누적하여 추정한다. 이는 계산량이 많고 효율성이 낮다.
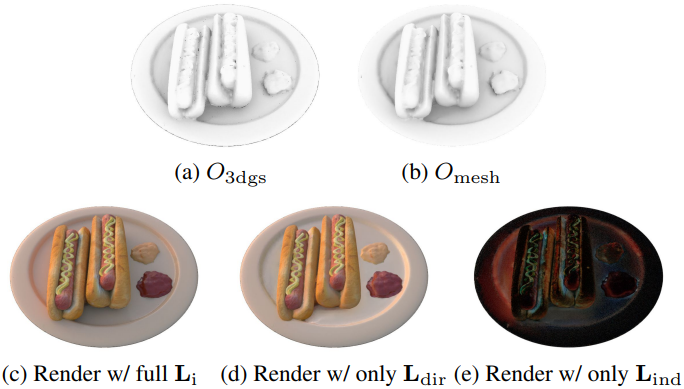
이와는 대조적으로, 본 논문에서는 명시적인 geometry guidance를 활용하여 deterministic한 메쉬 표면에서 추정되는 binary 항 \(O_\textrm{mesh} (\textbf{x}, \boldsymbol{\omega}_i) \in \{0, 1\}\)를 사용한다. 이 접근 방식은 효율적인 occlusion 평가를 위해 BVH로 가속화된 메쉬 기반 ray tracing을 가능하게 한다. 이러한 변경은 MGadapter가 3DGS와 메쉬 간의 모양 정렬을 보장하고, 이를 통해 근사화된 \(O_\textrm{mesh} (\textbf{x}, \boldsymbol{\omega}_i)\)와 실제 \(O_\textrm{3dgs} (\textbf{x}, \boldsymbol{\omega}_i)\) 간의 일관성을 유지하기 때문에 눈에 띄는 오차를 발생시키지 않는다.
4. Implementation Details
Loss Functions
GeoSplatting의 파이프라인은 완전히 미분 가능하며 photometric loss를 통해 end-to-end 학습이 가능하다. Geometry guidance 덕분에 정규화 항이 필요하지 않아 추가적인 geometry 제약 조건을 제공할 수 있다. 그러나 GeoSplatting은 명시적 표면을 최적화하는 것이 더 어렵기 때문에 object mask loss에도 의존한다. 구체적으로 photometric loss는 다음과 같이 계산된다.
\[\begin{equation} \mathcal{L}_\textrm{img} = \mathcal{L}_1 + \lambda_\textrm{SSIM} \mathcal{L}_\textrm{SSIM} + \lambda_\textrm{mask} \mathcal{L}_\textrm{mask} \end{equation}\](\(\mathcal{L}_\textrm{mask}\)는 렌더링된 alpha map과 GT object mask 사이의 MSE loss)
또한 DMTet과 FlexiCubes를 따라 entropy loss \(\mathcal{L}_\textrm{entropy}\)를 추가하여 모양을 제한한다. 더 나은 분해를 위해 NVdiffrecmc와 R3DG에 따라 조명 정규화 \(\mathcal{L}_\textrm{light}\)와 함께 \(\textbf{k}_d\)와 \(\textbf{k}_s\)에 smoothness 정규화 \(\mathcal{L}_\textrm{smooth}\)를 적용한다.
최종 loss $\mathcal{L}$은 photometric loss와 정규화 loss의 조합이다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{img} + \lambda_\textrm{entropy} \mathcal{L}_\textrm{entropy} + \lambda_\textrm{smooth} \mathcal{L}_\textrm{smooth} + \lambda_\textrm{light} \mathcal{L}_\textrm{light} \end{equation}\]Split-Sum Warm-up
PBR 방정식의 적분을 직접 계산하는 것은 비효율적이며, 특히 light transport 모델링에 사용된 geometry에 노이즈가 있는 학습 초기 단계에서 최적화 불안정성을 초래할 수 있다. 따라서 저자들은 기존 연구들을 참고하여 초기 학습 단계에서 split-sum approximation 기법을 적용했다. Split-sum approximation 기법은 self-occlusion을 가정하지 않으며, PBR 방정식을 다음과 같이 근사한다.
\[\begin{equation} \textbf{L}_o (\boldsymbol{\omega}_o) \approx \int_{\mathcal{H}^2} \textbf{f}_r (\boldsymbol{\omega}_i, \boldsymbol{\omega}_o) \vert \textbf{n} \cdot \boldsymbol{\omega}_i \vert \textrm{d} \boldsymbol{\omega}_i \cdot \int_{\mathcal{H}^2} \textbf{L}_\textrm{dir} (\boldsymbol{\omega}_i) D \vert \textbf{n} \cdot \boldsymbol{\omega}_i \vert \textrm{d} \boldsymbol{\omega}_i \end{equation}\]Split-sum approximation은 빠른 사전 계산을 가능하게 하여 평가 속도를 크게 향상시키지만, self-occlusion 모델링이 부족하여 최적이 아닌 분해 결과(ex. 그림자를 albedo에 baking)가 발생할 수 있다. 따라서 이 warm-up 단계 후, 그림자 효과와 inter-reflection을 통합하여 PBR 방정식을 더욱 정확하게 평가하기 위해 몬테카를로 샘플링 프로세스로 전환한다.
Appearance Refinement
GeoSplatting은 Gaussian별 shading을 수행한다. 즉, 먼저 Gaussian에 대해 PBR 색상을 계산한 다음, Gaussian별 색상을 픽셀로 rasterization한다. 각 Gaussian은 하나의 PBR 색상만 제공하기 때문에 표면 영역의 렌더링 디테일은 Gaussian 밀도에 의해 제한되어, 강한 반사와 같은 외형의 고주파 변화를 정확하게 모델링하기 어렵다. 이 문제는 특히 고도로 구조화된 Gaussian에서 두드러진다.

이 문제를 해결하기 위해, 저자들은 pixel-wise PBR을 수행하는 deferred shading 기법을 고려하였다. 학습 종료 시 deferred shading으로 전환하고 Gaussian의 변위를 약간 조정하도록 하였다.
Experiments
- 데이터셋: Synthetic4Relight, TensoIR Synthetic, Shiny Blender, Stanford-ORB
- NVIDIA 4090 1개에서 10~15분 소요
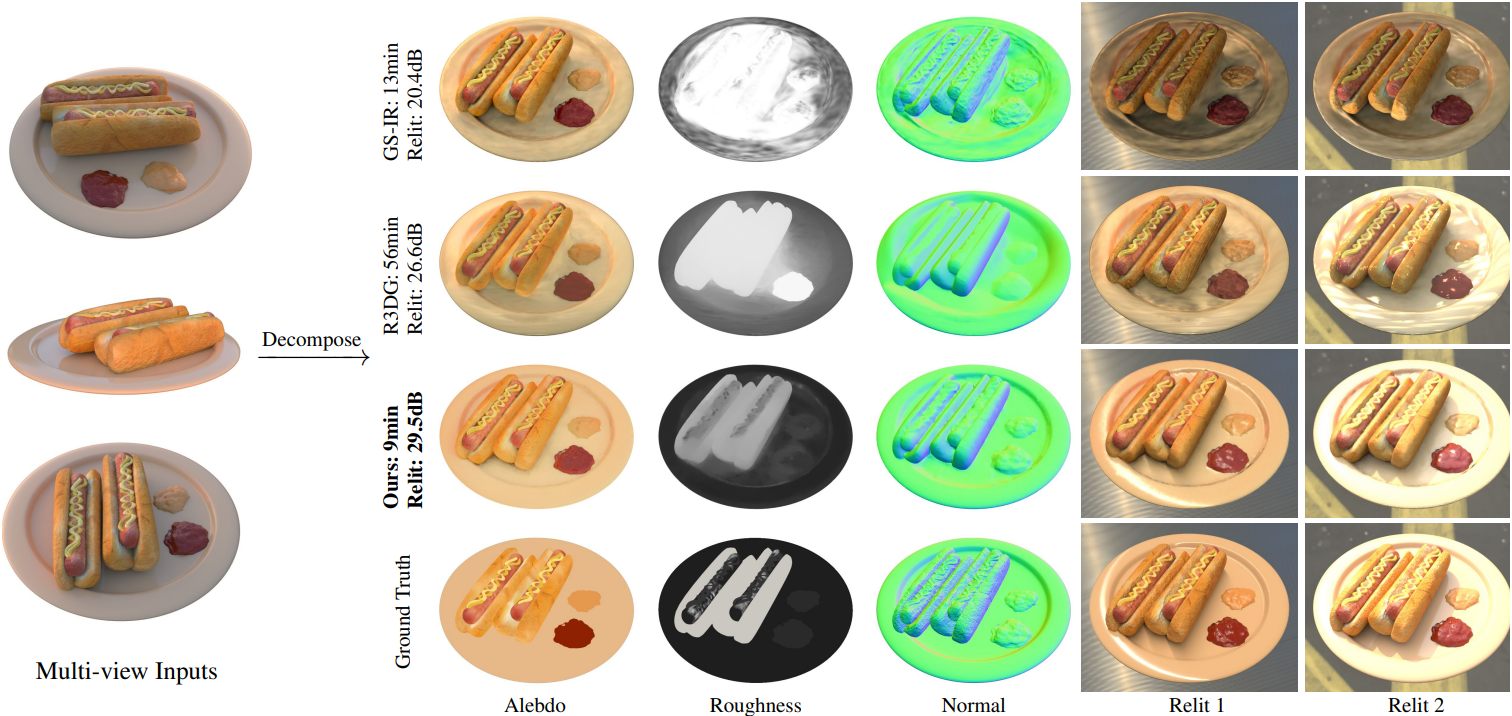
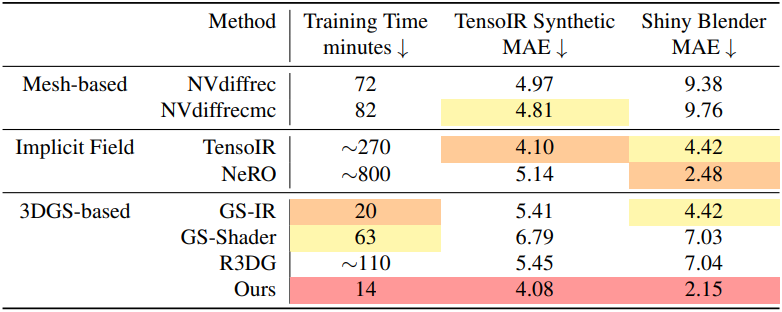
1. Inverse Rendering Performance


2. Normal Quality

3. Real-World Results

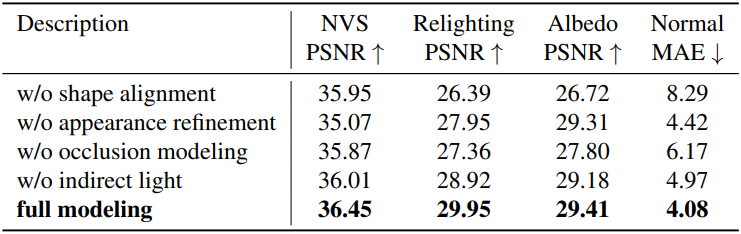
4. Ablation Studies