[논문리뷰] GaussianShader: 3D Gaussian Splatting with Shading Functions for Reflective Surfaces
CVPR 2024. [Paper] [Page] [Github]
Yingwenqi Jiang, Jiadong Tu, Yuan Liu, Xifeng Gao, Xiaoxiao Long, Wenping Wang, Yuexin Ma
ShanghaiTech University | The University of Hong Kong | Tencent America | Texas A&M University
29 Nov 2023

Introduction
3D Gaussian Splatting은 3D Gaussian 표현과 타일 기반 splatting 기술을 결합하여 고품질 3D 장면 모델링과 실시간 렌더링을 달성함으로써 실제 애플리케이션에서 뉴럴 렌더링 기술을 사용할 수 있게 되었다. 그러나 반사면이 있는 장면에서는 성능 저하가 발생한다. 이는 3D Gaussian Splatting이 모양 속성을 명시적으로 모델링하지 않아 중요한 뷰에 따른 변경 사항, 특히 specular highlight를 캡처하지 못하기 때문이다. 이러한 제약은 특히 눈에 띄는 반사 특성을 특징으로 하는 다양한 재료에 대하여 사실적인 렌더링을 달성하는 데 상당한 장애가 된다.
반사 표면을 정확하게 모델링하는 것은 어려운 task이다. Ref-NeRF와 ENVIDR은 암시적 표현에 shading function을 결합하고 반사 표면에 유망한 품질을 제공하였다. 그러나 시간이 많이 걸리는 최적화와 느린 렌더링 속도로 인해 어려움을 겪는다. SDF의 제한된 유연성으로 인해 ENVIDR은 복잡한 장면을 모델링하는 데 실패하고 일반 객체에 상당한 성능 저하를 나타낸다. 3D Gaussian Splatting 프레임워크에서 shading function을 결합하여 학습 및 렌더링의 효율성을 유지하면서 반사를 처리하는 능력을 향상시키는 방법은 아직 탐구되지 않은 문제이다.
본 논문에서는 3D Gaussian에 shading function을 통합하여 반사 표면이 포함된 장면 내에서 3D Gaussian의 뉴럴 렌더링을 향상시키는 새로운 방법인 GaussianShader를 제시하였다. GaussianShader의 효율성을 보장하려면 반사 모델링 능력을 유지하면서 shading function을 평가하는 데 비용이 많이 들 수 없다. 이에 비추어 저자들은 모든 복잡한 반사를 residual color 항에 포함시키면서 diffuse color와 direct reflection을 고려하는 새롭고 단순화된 shading function을 제안하였다. Direct reflection만 고려할 수 있는 Ref-NeRF의 shading function과 비교할 때, 이 residual color를 활용하면 GaussianShader가 보다 복잡한 반사 모양을 효율적으로 렌더링할 수 있다.
Shading function 계산의 또 다른 과제는 개별 3D Gaussian sphere에서 정확한 법선을 예측하는 방법이다. 첫째, 표면 법선을 계산하기 위해 3D Gaussian에서 국부적으로 연속적인 표면을 얻는 것이 어렵다. 둘째, 일반 계산을 위해 여러 3D Gaussian을 연결하는 것은 neighborhood searching을 사용하여 비용이 많이 든다. GaussianShader에서는 Gaussian sphere의 가장 짧은 축 방향을 기반으로 하고 이 축 방향의 normal residual을 학습하는 새로운 법선 표현을 도입하여 이 문제를 해결하였다. 그런 다음 추정된 법선과 Gaussian sphere로 공식화된 형상 사이의 일관성을 강화하기 위해 예측된 법선과 렌더링된 깊이에서 파생된 법선 사이에 효율적인 제약 조건을 도입한다. 법선 표현과 제약 조건 모두 Gaussian sphere의 정확한 법선 추정으로 이어지며, 이는 shading function을 계산하는 데 도움이 된다.
3D Gaussian Splatting을 기반으로 구축된 GaussianShader는 반사 표면과 같은 다양한 재질을 수용하면서 실시간 렌더링 속도를 유지한다. 이전 연구들과 비교하여 GaussianShader는 일반 장면과 반사 표면 모두에서 효율성과 강력한 성능 사이의 균형을 잘 유지한다.
Method

방법의 개요는 위 그림에 나와 있다. 본 논문의 접근 방식은 공분산 $\Sigma$, 불투명도 $\alpha$, 위치 $p$를 포함한 모양 속성을 포함하는 3D Gaussian sphere를 채택하는 것으로 시작된다. 반사에 대한 표현 능력을 향상시키기 위해 diffuse color, roughness(거칠기), specular tint, normal, residual color을 포함한 일련의 shading 속성이 필요한 shading function을 사용하여 이러한 Gaussian sphere의 모양을 계산한다. 이어서, 직접 조명(direct lighting)을 모델링하기 위해 미분 가능한 환경 조명 맵을 사용한다. Shading 프로세스는 정확한 법선 추정에 크게 의존한다.
1. Shading on 3D Gaussians
Gaussian Splatting은 빛-표면 상호 작용을 고려하지 않고 단순한 spherical harmonic (SH) 함수를 사용하여 Gaussian의 모양을 모델링한다. 따라서 Gaussian Splatting은 강한 반사 표면을 정확하게 표현하지 못한다. 그러나 빛-표면 상호 작용을 정확하게 고려하려면 렌더링 방정식의 정확한 평가가 필요하며, 이는 광범위한 계산 시간과 복잡한 BRDF 파라미터가 필요하다. 저자들은 훨씬 더 짧은 시간에 반사 표면에 대한 고품질 렌더링 결과를 얻을 수 있는 렌더링 방정식의 단순화된 근사치를 채택했다.
특히, Gaussian sphere의 경우 뷰 방향 $\omega_o$에 대해 렌더링된 색상 $c$는 다음과 같이 계산된다.
\[\begin{equation} \mathbf{c} (\omega_o) = \gamma (\mathbf{c}_d + \mathbf{s} \odot L_s (\omega_o, \mathbf{n}, \rho) + \mathbf{c}_r (\omega_o)) \end{equation}\]여기서 $\gamma$는 gamma tone 매핑 함수, \(\mathbf{c}_d \in [0, 1]^3\)은 이 Gaussian sphere의 diffuse color, $s \in [0, 1]^3$은 이 sphere에 정의된 specular tint, $L_s (\omega_o, \mathbf{n}, \rho)$는 이 방향에서 이 sphere에 대한 직접 반사광이다. $\mathbf{n}$은 이 Gaussian sphere의 법선이고, $\rho \in [0, 1]$는 sphere의 거칠기이며, \(\mathbf{c}_r : \mathbb{R}^3 \rightarrow \mathbb{R}^3\)은 residual color이고, $\odot$는 element-wise multiplication이다.
Diffuse color \(\mathbf{c}_d\)는 보는 방향에 따라 변하지 않는 이 Gaussian sphere의 일관된 색상이다. $\mathbf{s} \odot L_s (\omega_o, \mathbf{n}, \rho)$는 표면 고유 색상 $s$와 직접 반사광 $L_s$ 사이의 상호 작용을 설명한다. 이 항을 사용하면 렌더링 시 대부분의 반사를 표현할 수 있다. 간접광의 산란 및 반사와 같이 위의 직접광 반사로 설명할 수 없는 일부 반사가 여전히 있기 때문에 이러한 복잡한 반사를 설명하기 위해 residual color 항 \(\mathbf{c}_r (\omega_o)\)을 추가한다. 이와 달리 Ref-NeRF는 residual color 항 없이 shading function을 채택하므로 복잡한 반사를 처리하는 데 어려움을 겪는다. \(\mathbf{c}_r (\omega_o)\)는 SH 함수로 parameterize된다. \(\mathbf{c}_d\), $\mathbf{s}$, $\rho$, \(\mathbf{c}_r (\omega_o)\)의 SH 계수는 모두 이 Gaussian sphere와 관련된 학습 가능한 파라미터이다.
2. Specular Light
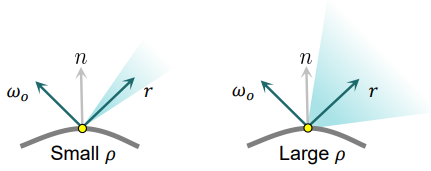
위 그림과 같이 specular GGX Normal Distribution Function $D$와 들어오는 radiance를 통합하여 반사광 $L_s$를 계산한다.
여기서 $\Omega$는 상부 반구 전체이고, $\Omega_i$는 입력 radiance의 방향이고, $D$는 specular lobe의 특성을 나타낸다. 표면이 거칠면 반사 방향 $\mathbf{r}$을 중심으로 specular lobe가 커지고, 표면이 매끄러우면 specular lobe가 작아진다. 반사 방향 $\mathbf{r}$은
\[\begin{equation} \mathbf{r} = 2(\omega_o \cdot \mathbf{n}) \mathbf{n} − \omega_o \end{equation}\]를 사용하여 뷰 방향 $\omega_o$와 법선 $\mathbf{n}$으로 계산된다. 환경 조명 $L(\omega_i)$은 학습 가능한 $6 \times 64 \times 64$ 큐브 맵으로 표현된다.
이 조명 적분은 여러 mipmap으로 사전 필터링되며, 각 mipmap에는 서로 다른 반사 방향과 서로 다른 거칠기의 조명 적분이 포함된다. 특정 거칠기와 특정 반사 방향에 대한 조명 적분을 계산하려면 mipmap에서 해당 값을 보간하기만 하면 된다. Integrated directional encoding으로 조명 적분을 계산하는 Ref-NeRF와 비교하여 여기서는 mipmap 기반의 조명 표현이 학습에 더 효율적이기 때문에 mipmap을 사용한다. 관찰 방향 $\omega_o$에 대한 반사 방향 $\mathbf{r}$을 얻으려면 Gaussian sphere에서 법선 $\mathbf{n}$을 추정해야 한다.
3. Normal Estimation
Gaussian sphere에 대한 법선 추정은 어렵다. Gaussian sphere는 개별 엔터티의 모음으로, 각각은 연속적인 표면이나 정의된 가장자리 없이 공간의 로컬한 점을 나타낸다. 이러한 이산적인 구조로 인해 일반적으로 연속적인 표면이 필요한 법선을 직접 계산하는 것이 본질적으로 어렵다. 저자들은 Gaussian의 가장 짧은 축 방향이 근사 법선 역할을 할 수 있다는 것을 관찰했으며 여기에 예측된 normal residual을 추가로 연관시켰다.
Shortest axis direction
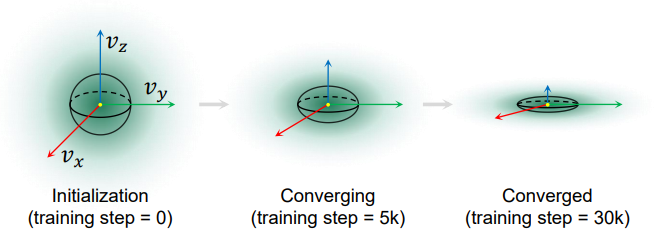
저자들은 실험에서 위 그림과 같이 최적화 과정에서 3D Gaussian sphere의 종횡비, 특히 가장 긴 축, 중간 축, 가장 짧은 축의 비율이 점차 증가한다는 흥미로운 관찰을 했다. 즉, Gaussian sphere가 점점 납작해지고 평면에 가까워진다. 이러한 관찰은 $\mathbf{v}$로 표시되는 이 평탄화된 Gaussian sphere의 법선으로 가장 짧은 축을 선택하도록 영감을 주었다.
Predicted normal residual
가장 짧은 축 $\mathbf{v}$는 대략적인 법선 역할만 한다. 정규 계산을 보다 정확하게 하기 위해 모든 Gaussian sphere에 학습 가능한 normal residual $\Delta \mathbf{n}$을 추가로 도입한다. 그러나 가장 짧은 축 $\mathbf{v}$의 방향은 가장 짧은 축의 방향이 표면에서 바깥쪽을 향할 수도 있고 안쪽을 향할 수도 있기 때문에 모호하다. 이러한 모호성을 처리하기 위해 두 시나리오를 모두 수용할 수 있도록 두 개의 normal residual을 최적화한다. 특정 뷰 방향 $\omega_o$가 주어지면 먼저 이 뷰 방향에 대한 법선 방향으로 뷰 방향 $\omega_o$와 정렬된 방향을 선택한 다음 해당 normal residual을 법선에 적용한다. 이 프로세스는 다음과 같이 설명된다.
\[\begin{equation} \mathbf{n} = \begin{cases} \mathbf{v} + \Delta \mathbf{n}_1 & \quad \textrm{if} \; \omega_o \cdot \mathbf{v} > 0 \\ -(\mathbf{v} + \Delta \mathbf{n}_2) & \quad \textrm{otherwise} \end{cases} \end{equation}\]Normal residual이 가장 짧은 축에서 너무 많이 벗어나는 것을 방지하기 위해 normal residual에 페널티를 추가하여 충분히 작은지 확인한다.
\[\begin{equation} \mathcal{L}_\textrm{reg} = \| \Delta \mathbf{n} \|^2 \end{equation}\]Normal-geometry consistency
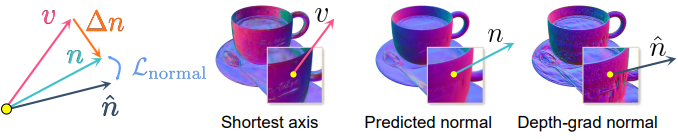
위의 가장 짧은 축 방향과 normal residual은 각 Gaussian sphere에 별도로 정의된다. 그러나 눈에 띄는 문제는 법선이 로컬 영역의 모든 Gaussian sphere와 연관되어 있다고 가정되는 로컬 형상의 기울기를 드러낸다는 것이다. 앞서 언급한 normal residual을 학습시키기 위해 단순히 color loss를 적용하면 로컬 형상과 추정된 법선 사이에 불일치가 발생한다. 주된 이유는 모든 Gaussian sphere가 이웃 Gaussian sphere에 의한 로컬한 형상을 알지 못한 채 개별적으로 normal residual을 학습하기 때문이다. 따라서 법선-형상 일관성을 보장하기 위해 로컬 영역의 여러 Gaussian sphere를 해당 법선과 연관시켜야 한다. 간단한 해결책은 공간에서 $K$개의 이웃을 검색하고 모든 이웃 sphere로부터 대략적인 법선을 추정하는 것이다. 그러나 이러한 KNN 검색은 모든 Gaussian sphere가 최적화 프로세스에서 동적으로 움직이기 때문에 학습 중에 비용이 매우 많이 든다. 대신, 저자들은 다음과 같이 법선-형상 일관성을 보장하는 간단하면서도 효과적인 방법을 제안하였다.
렌더링된 깊이 맵에서 파생된 grad normal과 예측 법선을 사용하여 렌더링된 법선 맵 간의 차이를 최소화하여 로컬 형상을 예측 법선과 연관시킨다.
\[\begin{equation} \mathcal{L}_\textrm{normal} = \| \bar{\mathbf{n}} - \hat{\mathbf{n}} \|^2 \end{equation}\]여기서 \(\bar{\mathbf{n}}\)는 렌더링된 normal map이고 \(\hat{\mathbf{n}}\)는 렌더링된 깊이 맵에 Sobel-like 연산자를 적용하여 계산된다. \(\hat{\mathbf{n}}\)는 렌더링된 깊이 맵에서 계산되기 때문에 여러 Gaussian sphere로 공식화된 로컬 형상을 나타낸다. \(\bar{\mathbf{n}}\)에는 각 Gaussian sphere에 별도로 정의된 법선의 정보가 포함되어 있다. 차이를 최소화함으로써 로컬 형상과 추정된 법선 간의 일관성을 강화한다.
4. Losses
\(\mathcal{L}_\textrm{color}\), \(\mathcal{L}_\textrm{normal}\), \(\mathcal{L}_\textrm{reg}\) 외에도 sparsity loss를 사용하여 Gaussian sphere의 불투명도 값 $\alpha$가 0 또는 1에 근접하도록 장려한다.
\[\begin{equation} \mathcal{L}_\textrm{sparse} = \frac{1}{\vert \alpha \vert} \sum_{\alpha_i} [\log (\alpha_i) + \log (1 - \alpha_i)] \end{equation}\]이러한 sparsity loss는 Gaussian sphere의 형상이 하나의 얇은 판으로 수렴되는 데 도움이 되며 렌더링 품질을 향상시킨다. 요약하면, 총 학습 loss $\mathcal{L}$은 다음과 같다.
\[\begin{equation} \mathcal{L} = \mathcal{L}_\textrm{color} + \lambda_n \mathcal{L}_\textrm{normal} + \lambda_s \mathcal{L}_\textrm{sparse} + \lambda_r \mathcal{L}_\textrm{reg} \end{equation}\]여기서 \(\lambda_n = 0.01\), \(\lambda_s = 0.001\), \(\lambda_r = 0.001\)이다.
Experiments
- 데이터셋: NeRF Synthetic, Shiny Blender, Glossy Synthetic, Tanks and Temples
- 구현 디테일
- optimizer: Adam
- iteration: 30,000
- GPU: NVIDIA RTX 3090
1. Comparisons
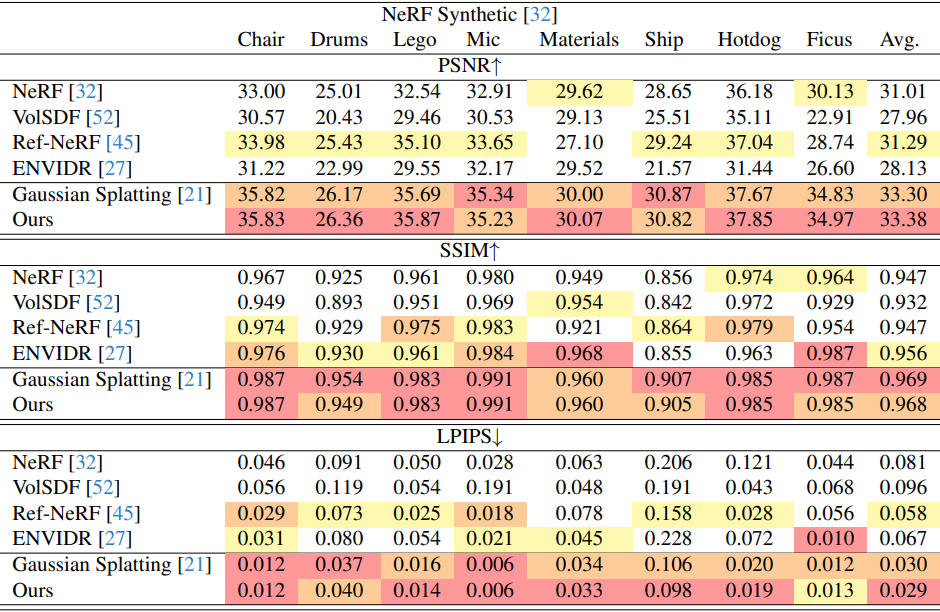
NeRF Synthetic dataset

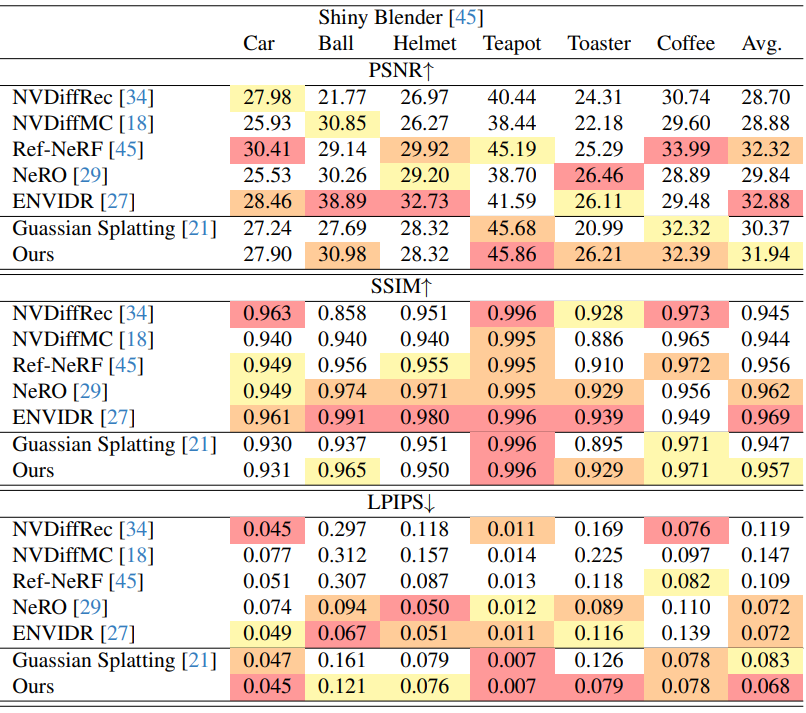
Shiny Blender dataset
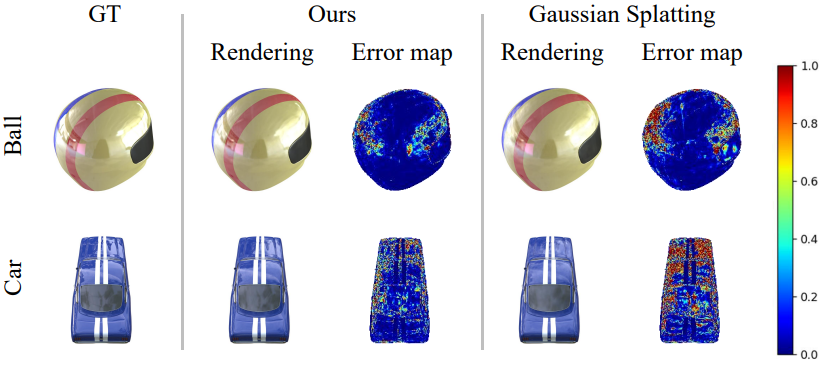
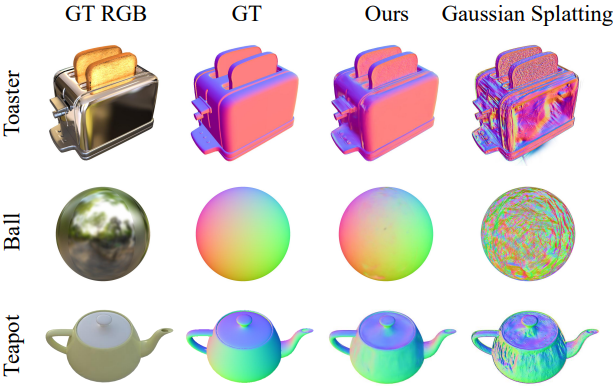
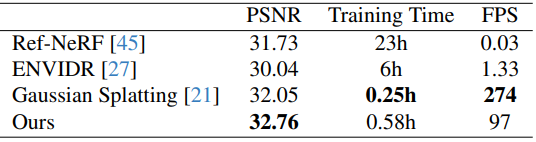
Tanks and Temples dataset

Glossy Synthetic dataset

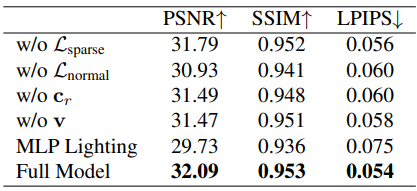
2. Ablation Study