Diffusion은 신이고 GPT는 무적이다

ICCV 2025. [Paper] [Page]
Andrew Bond, Jui-Hsien Wang, Long Mai, Erkut Erdem, Aykut Erdem
Koc University | Adobe Research | Hacettepe University
8 Jan 2025

Introduction

본 논문에서는 Gaussian을 사용하여 동영상을 모델링하기 위한 가벼운 프레임워크를 소개한다. 본 논문의 목표는 고품질의 효율적인 동영상 재구성을 달성하고, 프레임 보간, 공간적 리샘플링, 편집 등과 같은 다운스트림 애플리케이션을 지원하는 것이다. 이러한 애플리케이션을 구현하려면 Gaussian의 dynamics가 매우 semantic하고 일관성이 있어야 한다. 본 논문에서는 Gaussian의 이러한 semantic 이동이 보조 supervision 신호에 의해 강제되는 것이 아니라, 새로운 행동으로 나타나는 접근 방식을 모색하였다. 이는 이러한 supervision 신호 자체가 계산 비용이 높고 정확하게 추출하기 어려울 수 있기 때문이다. 또한, 표현 자체에서 선택된 디자인 선택의 부정적인 영향을 감출 수 있다. 이를 위해 본 논문에서는 동영상을 모델링하고 Gaussian의 움직임을 정규화하는 몇 가지 새로운 기법을 제안하였다.

본 논문에서는 장면 요소의 부드러운 궤적을 모델링하는 B-spline 기반 모션 표현을 도입하였으며, 모션의 로컬한 변화를 허용하면서 시간적 일관성을 보장한다. Gaussian 표현의 공간적 및 시간적 feature를 개선하여 기존 방법에 비해 재구성 품질이 향상되고 수렴 속도가 빠른 새로운 계층적 학습 전략을 제안하였다. 또한 neural ODE를 사용하여 연속적인 카메라 모션을 학습하는 접근 방식을 개발하여 미리 계산된 카메라 파라미터에 대한 의존성을 제거하고 다양한 캡처 설정에 대한 적응성을 향상시켰다.

본 논문의 방법은 메모리 사용량과 학습 시간을 크게 줄여 기존 접근 방식에 비해 더 낮은 계산 리소스로 표준 동영상 데이터셋에서 SOTA 성능을 달성하였다.

Method

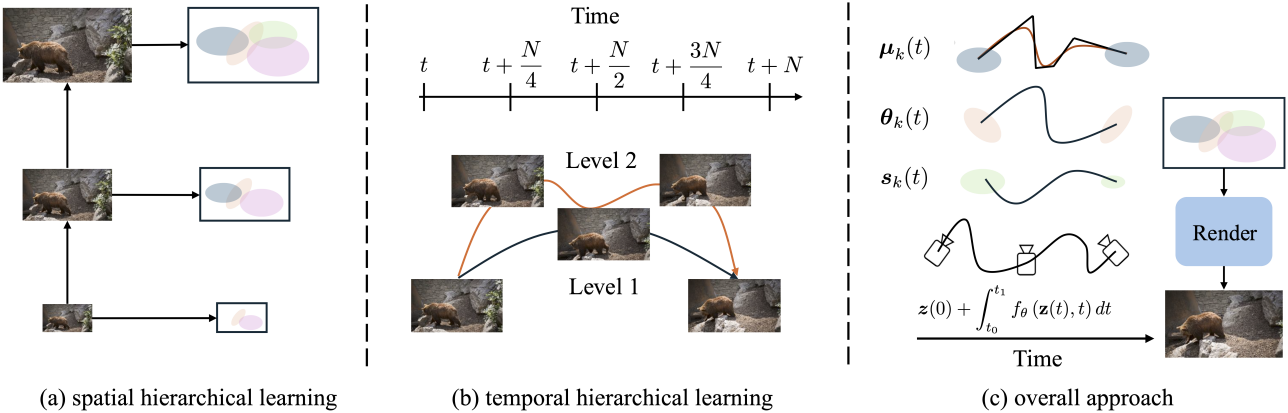
1. Adding Dynamics to the Gaussians

동영상에는 중복된 정보가 많이 포함되어 있다. 시간적 측면을 모델링하기 위해 Gaussian의 파라미터를 temporal basis function들로 보강한다.

위치 변화 모델링에 사용되는 것과 같은 기존 다항식 basis는 U자형과 같은 단순한 궤적에도 overfitting 및 재구성 오차를 유발할 수 있다. 이는 저차 다항식 하나로는 복잡한 궤적, 특히 장시간 또는 많이 동적인 영상의 궤적을 잘 근사할 수 없기 때문이다. 고차 다항식은 불안정하고 noise에 민감한 것으로 알려져 있다. 기본적인 cubic B-spline들을 간단히 적용하면 이 문제를 크게 완화할 수 있음을 보인다. 구체적으로, $n$번째 Gaussian의 위치를 ​​시간 의존적인 함수로 모델링한다.

\[\begin{equation} \mu_n (t) = \sum_{t=0}^n N_{i,p}(t) \textbf{P}_{n,i} \end{equation}\]

(\(\textbf{P}_{n,i} \in \mathbb{R}^d\)는 $i$번째 control point, \(N_{i,p}(t)\)는 basis function, $p = 3$, $N$은 control point 개수)

본 논문에서는 clamped B-spline을 사용하므로 처음 $p+1$개의 knot은 0으로 고정되고 마지막 $p+1$개의 knot은 1로 고정된다. 나머지 knot들은 균등한 간격으로 배치된다.

대조적으로, 공분산, 색상, 불투명도와 같은 다른 자유도의 경우 의도적으로 표현력이 낮은 모델을 사용한다. 이는 불투명도와 scaling이 극적으로 변하도록 허용하면 재구성 loss로 인해 Gaussian이 무의미해지는 경향이 있기 때문이다. 따라서 불투명도가 시간에 따라 변하는 것을 항상 허용하지 않아 불투명도가 낮은 Gaussian이 훨씬 줄어든다. 공분산의 경우, scaling과 rotation을 모델링하기 위해 3차 다항식을 사용한다.

Gaussian의 색상을 모델링하는 데 널리 사용되는 방법은 학습된 MLP를 사용하는 것이다. 그러나 약한 MLP일지라도 Gaussian이 동영상의 개체를 따라 움직이기보다는 색상을 변화시키는 경향이 있다. 따라서 시간에 따른 색상 변화도 허용하지 않는다.

요약하면, $n$번째 Gaussian의 dynamics는 다음과 같이 parametrize되어 동영상의 모션을 적절하게 포착하면서도 모델링 효율성과 표현의 semantic을 유지한다.

\[\begin{equation} \tilde{\mathcal{G}}_n (t) = \mathcal{G}_n \left( \underbrace{\mu_n (t)}_{\textrm{B-splines}}, \underbrace{\Sigma_n (t)}_{\textrm{3rd-order polynomials}}, \underbrace{c_n}_{\textrm{constant}}, \underbrace{o_n}_{\textrm{constant}} \right) \end{equation}\]

2. Hierarchical Representations of the Gaussians

본 논문에서는 최적화를 각기 다른 세부 수준을 목표로 하는 discrete한 단계로 분해하는 방안을 제안하였다. Coarse한 단계부터 fine한 단계까지 다양한 공간적 및 시간적 스케일에서 점진적으로 표현을 구축함으로써, 글로벌한 구조와 로컬한 디테일을 모두 포착하는 동시에 시간에 따른 부드럽고 자연스러운 모션을 보여주는 Gaussian 동영상 모델을 구성할 수 있다.

Spatial Hierarchical Learning

공간에 대한 계층적 학습을 위해 Gaussian 피라미드를 사용한다. Gaussian 피라미드는 동일한 이미지의 여러 레벨을 포함하고 있으며, 각 레벨은 Gaussian 커널을 사용하여 점진적으로 다운샘플링된 버전을 가지고 있다. 직관적으로 피라미드의 하위 레벨(더 높은 해상도)에 있는 점은 커널 선택으로 인해 상위 레벨(더 낮은 해상도)에서 하나의 Gaussian으로 완벽하게 표현될 수 있기 때문에 이는 Gaussian splatting 프레임워크에 자연스럽게 들어맞는다.

상위 레벨이 하위 레벨로 다시 projection될 때, 변경해야 할 유일한 것은 이 Gaussian의 스칼라 scale이다. 이러한 근거를 사용하여 가장 높은 레벨에서 학습을 시작하여 수렴할 때까지 학습시킨다. 그런 다음 한 레벨 아래로 이동하여 더 많은 Gaussian을 도입하고 다시 수렴할 때까지 학습시킨다. 피라미드의 모든 $N_p$개의 레벨이 학습될 때까지 이 프로세스를 반복한다.

Temporal Hierarchical Learning

프레임 보간과 같은 다운스트림 애플리케이션에 유용한 부드러운 모션을 촉진하기 위해, B-spline 기반 점진적 프레임 샘플링 방식을 채택하였다. 먼저 모든 N번째 프레임에서 학습을 시작한 후, 시간 해상도를 점진적으로 높이고, 선택적으로 B-spline knot을 개선하여 학습된 Gaussian 모션을 방해하지 않으면서 추가적인 유연성을 제공한다.

3. Modeling Camera Motion

지금까지 설명한 접근 방식은 카메라 모션이 없는 동영상에서는 잘 작동하지만, 약간의 카메라 이동에도 민감하게 반응한다. 기존 접근 방식은 일반적으로 COLMAP과 같은 SfM 알고리즘을 사용하여 카메라 파라미터를 추정하였다. 그러나 동영상에서는 제한된 시점으로 인해 카메라 모션을 정확하게 재구성하기 어렵기 때문에 이 알고리즘의 신뢰성이 떨어질 수 있다. 더욱이, COLMAP은 속도가 느려 학습 효율에 병목 현상을 일으킨다.

이러한 문제를 해결하기 위해, 동영상 재구성 파이프라인 내에서 카메라 파라미터를 직접 학습하는 간단하면서도 효과적인 접근법을 제안하였다. 프레임워크의 forward pass는 이미 전체 렌더링 프로세스를 포괄하고 있으므로, 핵심 통찰력은 intrinsic 파라미터와 extrinsic 파라미터를 모두 명시적으로 학습하여 Gaussian 렌더링에 사용할 수 있다는 것이다. 구체적으로, intrinsic 파라미터는 동영상 전체에 걸쳐 상수를 유지한 채 모델링하고, extrinsic 파라미터는 neural ODE를 사용하여 모델링한다.

Experiments

  • 데이터셋: DL3DV, DAVIS Tap-Vid benchmark
  • 구현 디테일
    • 총 iteration: 50,000
    • Gaussian 수: 40만
    • learning rate: 0.01 (weight decay = 0.99995)
    • optimizer: Adam
    • Gaussian은 카메라 너비와 높이의 3배 radius로 랜덤 초기화
    • 15,000 iteration에 계층적 학습을 1번 사용
      • 10만 개의 새로운 Gaussian을 추가
    • 5,000 iteration마다 어떠한 프레임에도 나타나지 않는 Gaussian을 첫 번쨰 프레임으로 보내 spline의 평균을 조정 (30,000 iteration까지)

1. Experimental Results

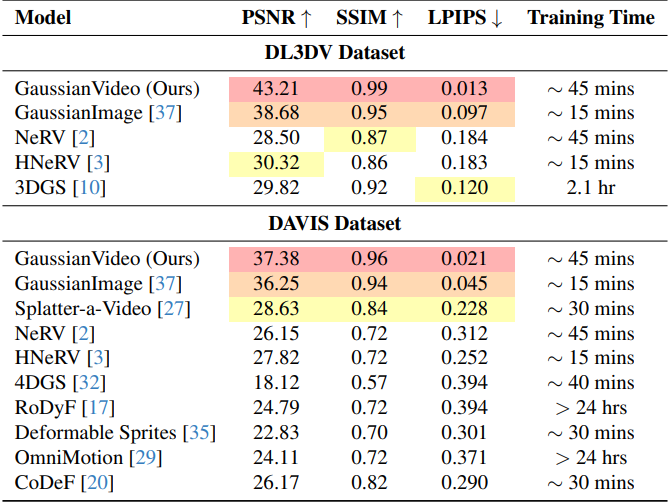
다음은 다른 방법들과 비교한 결과이다.

2. Analysis

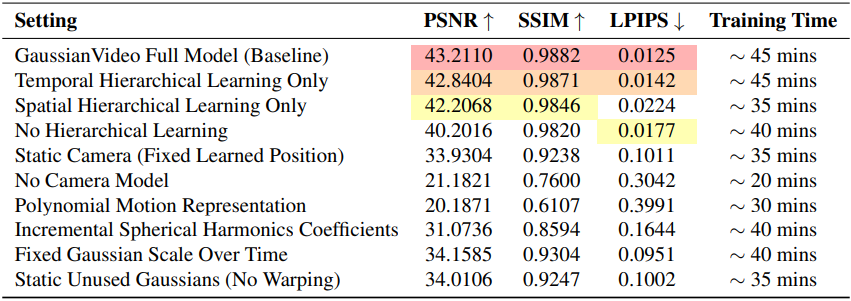
다음은 DL3DV에서의 ablation study 결과이다.


다음은 Gaussian 수에 따른 성능을 비교한 그래프이다.


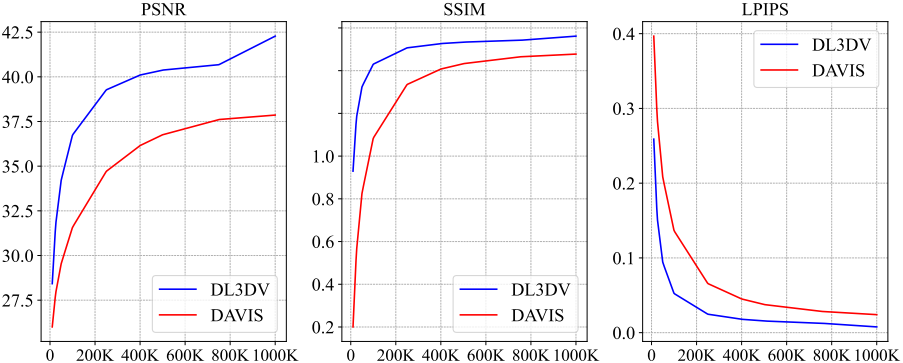
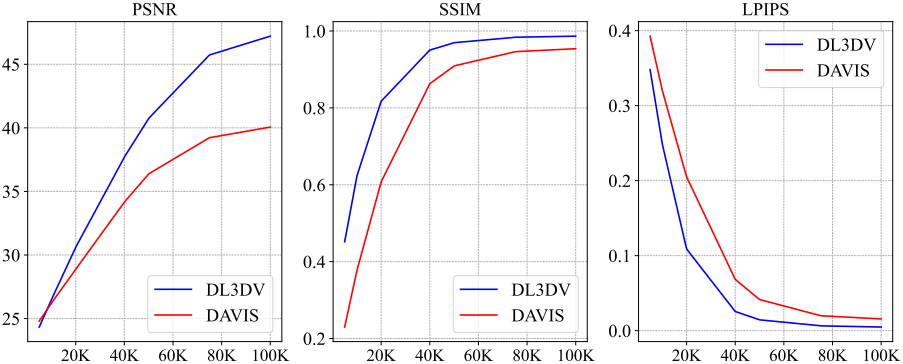
다음은 학습 길이에 따른 성능을 비교한 그래프이다.

3. Applications

다음은 연속적인 모션에 대한 프레임 보간 예시이다.


다음은 학습된 동영상에 대한 공간적 리샘플링 예시이다.


다음은 동영상 stylization 예시이다.

You may also enjoy