[논문리뷰] GaussianPro: 3D Gaussian Splatting with Progressive Propagation
arXiv 2024. [Paper] [Page] [Github]
Kai Cheng, Xiaoxiao Long, Kaizhi Yang, Yao Yao, Wei Yin, Yuexin Ma, Wenping Wang, Xuejin Chen
University of Science and Technology of China | The University of Hong Kong | Nanjing University | The University of Adelaide | ShanghaiTech University | Texas A&M University
22 Feb 2024

Introduction
Novel view synthesis는 캡처된 장면에서 새로운 시점의 이미지를 생성하는 것을 목표로 하는 컴퓨터 비전 및 컴퓨터 그래픽스에서 중요하지만 어려운 작업이다. 최근 NeRF는 이 task를 크게 향상시켜 3D 장면, 텍스처 및 조명을 명시적으로 모델링하지 않고도 충실도가 높은 렌더링을 달성했다. 그러나 다양한 노력이 있었음에도 불구하고 무거운 볼륨 렌더링 방식으로 인해 NeRF는 여전히 렌더링 속도가 느린 문제를 겪고 있다.
실시간 뉴럴 렌더링을 달성하기 위해 3DGS가 개발되었다. 학습 가능한 속성을 갖춘 3D Gaussian으로 명시적으로 장면을 모델링하고 Gaussian의 rasterization을 수행하여 렌더링을 생성한다. Splatting 전략은 시간이 많이 소요되는 광선 샘플링을 방지하고 병렬로 계산되므로 효율성이 높고 렌더링 속도가 빠르다. 3DGS는 Gaussian의 위치, 색상, 모양을 초기화하기 위해 Structure-from-Motion (SfM) 기술로 생성된 sparse한 포인트 클라우드에 크게 의존한다. 또한 장면을 완벽하게 커버하기 위해 더 많은 새로운 Gaussian을 생성하는 복제(clone) 및 분할(split) 전략이 있다.
그러나 3D Gaussian을 생성하기 위한 densification 전략에는 두 가지 주요 제한 사항이 있다.
- Gaussian 초기화에 민감하다. SfM 기술은 항상 3D 포인트를 생성하지 못하고 텍스처가 없는 영역을 비워 두므로 densification 전략은 잘못된 초기화로 장면을 덮을 수 있는 신뢰할 수 있는 Gaussian을 생성하는 데 어려움을 겪는다.
- 기존 재구성된 geometric prior를 무시한다. 새로운 Gaussian은 이전 Gaussian과 동일하게 복제되거나 임의의 위치와 방향으로 초기화된다. 덜 제한된 densification은 3D Gaussian 최적화에 어려움을 초래하며, 텍스처가 없는 영역에서는 Gaussian이 거의 없어 결국 렌더링 품질이 저하된다.
3DGS의 결과에는 잡음이 많은 Gaussian이 포함되어 있으며 일부 영역은 충분한 Gaussian으로 덮이지 않는다.
본 논문에서는 보다 작고 정확한 3D Gaussian을 생성하여 특히 텍스처가 없는 표면에서 렌더링 품질을 향상시킬 수 있는 새로운 progressive propagation 전략을 제안하였다. 핵심 아이디어는 재구성된 장면 형상을 prior로 완전히 활용하고 고전적인 패치 매칭 기술로 정확한 위치와 방향을 가진 새로운 Gaussian을 점진적으로 생성하는 것이다.
구체적으로 3D 공간과 2D 이미지 공간 모두에서 Gaussian 밀도를 고려한다. 각 입력 이미지에 대해 알파 블렌딩을 통해 3D Gaussian의 위치와 방향을 누적하여 depth map과 normal map을 렌더링한다. 이웃 픽셀이 비슷한 깊이와 normal 값을 공유할 가능성이 있다는 관찰에 기반으로, 픽셀에 대해 이웃 픽셀의 깊이와 법선 값을 이 픽셀에 반복적으로 전파(propagate)하여 후보들의 집합을 공식화한다. 고전적인 패치 매칭 기술을 활용하여 멀티뷰 photometric consistency 제약 조건을 충족하는 최상의 후보를 선택하여 각 픽셀에 대한 새로운 깊이와 법선(전파된 깊이/법선이라고 함)을 생성한다. 전파된 깊이가 렌더링된 깊이와 크게 다른 픽셀을 선택한다. 큰 차이는 기존 3D Gaussian이 실제 형상을 정확하게 캡처하지 못할 수 있음을 의미하기 때문이다. 결과적으로 전파된 깊이를 사용하여 선택한 픽셀을 3D 공간으로 명시적으로 역투영(back-project)하고 새 Gaussian으로 초기화한다. 또한 전파된 법선을 활용하여 3D Gaussian의 방향을 정규화하여 재구성된 3D 지오메트리 및 렌더링 품질을 더욱 향상시킨다.
본 논문이 제안한 progressive propagation 전략은 잘 모델링된 영역에서 덜 모델링된 영역으로 정확한 기하학적 정보를 전송하여 보다 작고 정확한 3D Gaussian을 생성할 수 있다. 본 논문의 방법은 3DGS와 비교하여 더 정확하고 컴팩트한 Gaussian을 생성하므로 3D 장면의 더 나은 커버리지를 달성한다. 또한 Waymo 및 MipNeRF360과 같은 공개 데이터셋에서 3DGS의 성능을 크게 향상시키는 것으로 확인되었다.
Method
1. Overview
본 논문에서는 정확한 위치와 방향을 갖는 3D Gaussian을 명시적으로 생성하여 렌더링 품질과 컴팩트성을 향상시키는 새로운 progressive propagation 전략을 제안하였다. 저자들은 3D 공간과만 결합하는 대신 3D 공간과 2D 이미지 공간 모두에서 이 문제를 해결할 것을 제안하였다. 3D Gaussian을 2D 공간에 투영하여 Gaussian의 성장을 가이드하는 데 사용되는 depth map과 normal map을 생성한다. 그런 다음 이웃 픽셀에서 전파된 값을 기반으로 각 픽셀의 깊이와 normal을 반복적으로 업데이트한다. 새로운 깊이가 초기 깊이와 크게 다른 픽셀은 3D 점으로 3D 공간에 다시 투영되고 이러한 점은 새로운 Gaussian으로 추가로 초기화된다. 또한 planar loss도 통합되어 Gaussian의 형상을 더욱 정규화하여 보다 정확한 형상을 생성한다.
2. Hybrid Geometric Representation
본 논문은 3D Gaussian을 뷰에 따른 2D depth map 및 normal map과 결합한 하이브리드 기하학적 표현을 제안하였다. 여기서 2D 표현은 Gaussian의 densification을 지원하는 데 활용된다.
3D Gaussian의 discrete하고 불규칙한 토폴로지로 인해 로컬한 표면에서 인접한 Gaussian을 검색하는 것과 같이 형상의 연결성을 인식하는 것이 어렵다. 결과적으로 Gaussian densification을 가이드하는 현재의 형상을 인식하기가 어렵다. 저자들은 고전적인 multi-view stereo(MVS) 방법에서 영감을 받아 3D Gaussian을 구조화된 2D 이미지 공간에 매핑하여 이 문제를 해결할 것을 제안하였다. 이 매핑을 통해 Gaussian의 이웃을 효율적으로 결정하고 그들 사이에 기하학적 정보를 전파할 수 있다. 특히, Gaussian이 3D 공간에서 동일한 로컬 평면에 위치하는 경우 2D projection도 인접한 영역에 있어야 하며 유사한 기하학적 특성(ex. 깊이, normal)을 나타내야 한다.
Gaussian의 깊이 값
Camera extrinsics이 $[\mathbf{W}, \mathbf{t}] \in \mathbb{R}^{3 \times 4}$인 각 시점에 대해 Gaussian $G_i$의 중심 \(\boldsymbol{\mu}_i\)는 카메라 좌표계에 \(\boldsymbol{\mu}_i^\prime\)로 projection될 수 있다.
\[\begin{equation} \boldsymbol{\mu}_i^\prime = \begin{bmatrix} x_i \\ y_i \\ z_i \end{bmatrix} = \mathbf{W} \boldsymbol{\mu}_i + \mathbf{t} \end{equation}\]여기서 $z_i$는 현재 시점에서 Gaussian의 깊이를 나타낸다.
Gaussian의 normal 값
Gaussian $G_i$에서 공분산 행렬은 \(\boldsymbol{\Sigma}_i = \mathbf{R}_i \mathbf{S}_i \mathbf{S}_i^\top \mathbf{R}_i^\top\)이다. Rotation matrix \(\mathbf{R}_i\)는 세 개의 orthogonal eigenvector를 결정하며, scaling matrix \(\mathbf{S}_i \in \mathbb{R}^{3 \times 3}\)는 eigenvector의 각 방향에 대한 scale을 결정한다. 3D Gaussian의 \(\boldsymbol{\Sigma}_i\)는 타원체의 모양 표현과 비교할 수 있다. 여기서 eigenvector는 타원체의 축에 해당하고 scale은 축의 길이를 나타낸다. GaussianShader에 따르면 Gaussian은 최적화 과정에서 점차적으로 평탄화되어 평면에 가까워진다. 따라서 가장 짧은 축의 방향은 Gaussian의 normal 방향 \(\mathbf{n}_i\)를 근사할 수 있다.
\[\begin{equation} \mathbf{n}_i = \mathbf{R}_i [r, :], \quad r = \arg \min ([s_1, s_2, s_3]) \\ \textrm{where} \quad \textrm{diag} (s_1, s_2, s_3) = \mathbf{S}_i \end{equation}\]현재 시점에서의 2D depth map과 normal map은 알파 블렌딩을 기반으로 렌더링되며, 속성 색상 \(\mathbf{c}_i\)를 Gaussian의 깊이 $z_i$와 normal $\mathbf{n}_i$로 대체하여 계산한다.
3. Progressive Gaussian Propagation
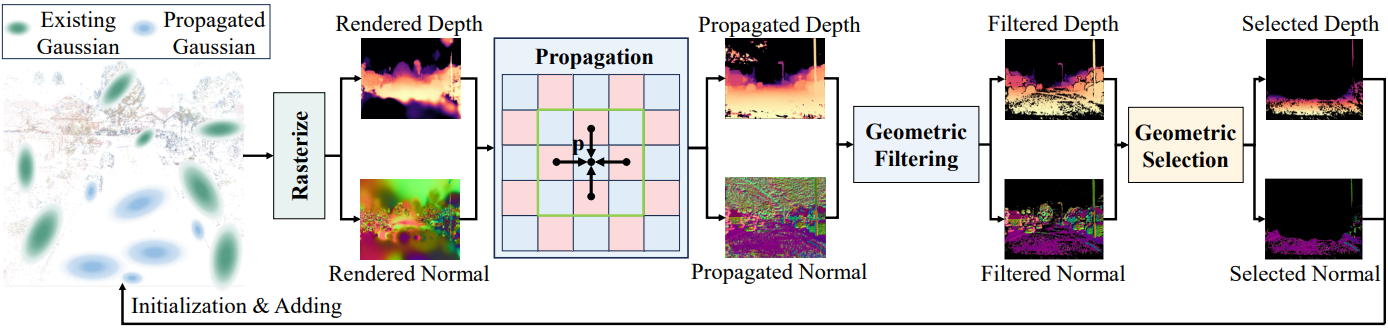
본 논문은 잘 모델링된 영역에서 덜 모델링된 영역으로 정확한 형상을 전파하여 새로운 Gaussian을 생성할 수 있는 progressive gaussian propagation 전략을 도입하였다. 위 그림에서 볼 수 있듯이 렌더링된 depth map과 normal map을 사용하여 패치 매칭으로 이웃 픽셀의 깊이와 normal 정보를 현재 픽셀로 전파한다. 이는 새로운 깊이와 normal을 생성하며, 이를 propagated depth와 proopagated normal이라 부른다. 더 많은 Gaussian이 필요한 픽셀을 선택하고 propagated depth와 propagated norma을 활용하여 새로운 Gaussian을 초기화하기 위해 기하학적 필터링 및 선택 연산을 추가로 수행한다.
Plane Definition
Propagation을 위해서 먼저 각 픽셀의 깊이와 normal을 3D 로컬 평면으로 변환해야 한다. 좌표가 $\mathbf{p}$인 각 픽셀에 대해 3D 로컬 평면은 $d, \mathbf{n})$으로 parameterize된다. 여기서 $\mathbf{n}$은 픽셀의 렌더링된 normal이고 $d$는 카메라 좌표의 원점에서 로컬 평면까지의 거리로 다음과 같이 계산된다.
\[\begin{equation} d = z \mathbf{n}^\top \mathbf{K}^{-1} \tilde{\mathbf{p}} \end{equation}\]여기서 $\tilde{\mathbf{p}}$는 $\mathbf{p}$의 homogeneous coordinate이고, $z$는 픽셀의 렌더링된 깊이, $\mathbf{K}$는 camera intrinsic이다.
Candidate Selection
3D 로컬 평면을 정의한 후 propagation을 위해 각 픽셀의 이웃을 선택해야 한다. ACMH에 정의된 체커보드 패턴을 따라 인접 픽셀을 선택한다. 픽셀의 propagation의 설명을 위해 가장 가까운 4개의 픽셀을 사용한다고 하자. 각 픽셀에 대해 평면 후보들의 집합 \(\{(d_{k_l}, \mathbf{n}_{k_l}) \, \vert \, l \in \{0, 1, 2, 3, 4\}\}\)는 propagation을 통해 획득된다. 여기서 $k_l$은 픽셀 $p$와 그에 인접한 4개의 픽셀의 인덱스이다.
Patch Matching
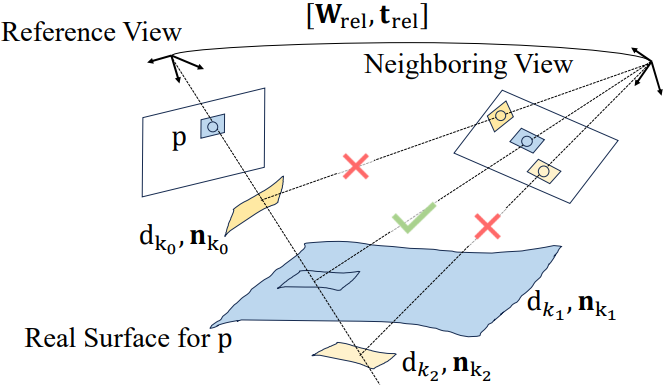
평면 후보를 얻은 후, 패치 매칭을 통해 각 픽셀에 대한 최적의 평면을 결정한다. 좌표가 $\mathbf{p}$인 픽셀 $p$의 경우 각 평면 후보 $(d_{k_l}, \mathbf{n}_{k_l})$를 기반으로 homography transformation $\mathbf{H}$가 수행되며, 이는 다음과 같이 이웃 프레임에서 $\mathbf{p}$를 $\mathbf{p}^\prime$으로 워프시킨다.
여기서 \(\tilde{\mathbf{p}}^\prime\)는 \(\tilde{\mathbf{p}}\)의 homogeneous coordinate이고 $\mathbf{H}$는 다음 식으로 얻을 수 있다.
\[\begin{equation} \mathbf{H} = \mathbf{K} \bigg( \mathbf{W}_\textrm{rel} - \frac{\mathbf{t}_\textrm{rel} \mathbf{n}_{k_l}^\top}{d_{k_l}} \bigg) \mathbf{K}^{-1} \end{equation}\]여기서 \([\mathbf{W}_\textrm{rel}, \mathbf{t}_\textrm{rel}]\)는 레퍼런스 뷰에서 인접 뷰까지의 상대적 변환이다. 마지막으로 $p$와 $p^\prime$의 색상 일관성은 NCC(Normalized Cross Correlation)를 기반으로 평가된다. $p$의 로컬 평면은 색상 일관성이 가장 좋은 평면 후보로 업데이트된다. 위 그림은 이 프로세스의 직관적인 시각화이다. 평면 후보에 대한 propagation은 넓은 지역에 걸쳐 효과적인 기하학적 정보를 전송하기 위해 $u$번 반복된다. 그런 다음 픽셀의 깊이와 normal이 전파된 평면에서 업데이트되어 궁극적으로 propagated depth map과 propagated normal map이 생성된다.
Geometric Filtering and Selection
전파된 결과의 불가피한 오차로 인해 COLMAP의 multi-view geometric consistency check를 통해 부정확한 깊이와 normal을 필터링하고 필터링된 depth map과 normal map을 얻는다. 마지막으로 필터링된 깊이와 렌더링된 깊이 사이의 상대적 차이를 계산한다. Threshold $\sigma$보다 큰 차이가 있는 영역의 경우 기존 Gaussian이 이러한 영역을 정확하게 모델링하지 못하는 것으로 간주한다. 따라서 이 영역의 픽셀을 3D 공간으로 다시 projection하고 3DGS와 동일한 초기화를 사용하여 3D Gaussian으로 초기화한다. 그런 다음 이러한 Gaussian은 추가 최적화를 위해 기존 Gaussian에 추가된다.
Plane Constraint Optimization

원래 3DGS에서 최적화는 기하학적 제약 조건을 통합하지 않고 이미지 재구성 loss에만 의존한다. 결과적으로 최적화된 Gaussian 모양은 실제 표면 형상에서 크게 벗어날 수 있다. 이러한 편차는 새로운 시점에서 볼 때 렌더링 품질 저하로 이어지며, 특히 시야가 제한된 대규모 장면의 경우 더욱 그렇다. 위 그림에서 볼 수 있듯이 3DGS의 Gaussian 모양은 도로의 기하학적 구조와 크게 다르므로 새로운 시점에서 볼 때 심각한 렌더링 아티팩트가 발생한다. 저자들은 Gaussian의 모양이 실제 표면과 매우 유사하도록 장려하는 평면 제약 조건을 제안하였다. 특히 앞서 구한 propagated 2D normal map은 장면의 평면 방향을 나타낸다. L1 loss와 angular loss를 사용하여 Gaussian의 렌더링된 normal과 propagated normal 간의 일관성을 명시적으로 적용한다.
여기서 $\hat{N}$은 렌더링된 normal map, $\tilde{N}$은 propagated normal map, $Q$는 기하학적 필터링 후의 유효한 픽셀 집합이다.
또한 Gaussian의 가장 짧은 축이 normal 방향을 나타낼 수 있도록 NeuSG의 스케일 정규화 loss \(\mathcal{L}_\textrm{scale}\)을 통합했다.
\[\begin{equation} \mathcal{L}_\textrm{scale} = \| \min (s_1, s_2, s_3) \|_1 \end{equation}\]이 loss는 Gaussian의 최소 scale을 0에 가깝게 제한하여 Gaussian을 효과적으로 평면 모양으로 만든다. 마지막으로 평면 제약 조건은 두 loss의 가중 합으로 표현될 수 있다.
\[\begin{equation} \mathcal{L}_\textrm{planar} = \beta \mathcal{L}_\textrm{normal} + \gamma \mathcal{L}_\textrm{scale} \end{equation}\]Training Strategy
$m = 50$ iteration마다 progressive propagation 전략을 사용하여 3DGS에 이 전략을 통합한다. Propagated normal map은 평면 제약 loss를 계산하기 위해 저장된다. 최종 loss $\mathcal{L}$은 평면 제약 loss와 3DGS의 이미지 재구성 loss \(\mathcal{L}_1\) 및 \(\mathcal{L}_\textrm{D-SSIM}\)으로 구성된다.
\[\begin{equation} \mathcal{L} = (1 - \lambda) \mathcal{L}_1 + \lambda \mathcal{L}_\textrm{D-SSIM} + \mathcal{L}_\textrm{planar} \end{equation}\]여기서 가중치 $\lambda$는 3DGS와 동일하게 0.2로 설정된다.
Experiment
- 데이터셋: Waymo, MipNeRF360
- 구현 디테일
- iteration: 30,000
- 3DGS의 학습 스케줄과 hyperparameter를 따름
- 3DGS의 densification (clone & split) 대신 progressive propagation을 사용
- $m = 50$ iteration마다 propagation이 3번씩 수행됨
- $\sigma = 0.8$, $\beta = 0.001$, $\gamma = 100$
- GPU: RTX 3090 1개
1. Quantative and Qualitative Results
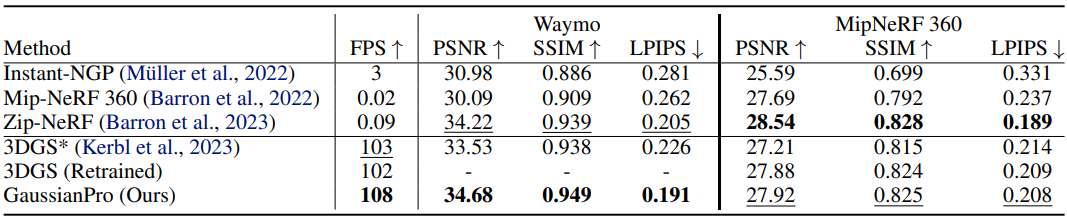
다음은 Waymo와 MipNeRF360 데이터셋에서의 결과를 기존 방법들과 비교한 것이다.

2. Ablation Study
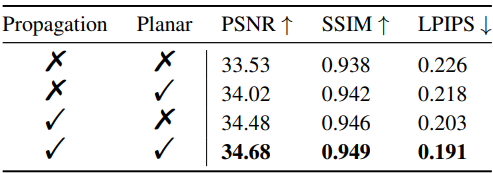
다음은 progressive propagation 전략과 평면 제약 조건에 대한 ablation 결과이다.

다음은 여러 학습 뷰 비율에 따른 결과를 3DGS와 비교한 표이다.

다음은 MipNeRF360 데이터셋의 Room scene의 Gaussian을 시각화한 것으로, GaussianPro가 noisy한 Gaussian을 덜 포함하고 더 컴팩트한 것을 볼 수 있다.

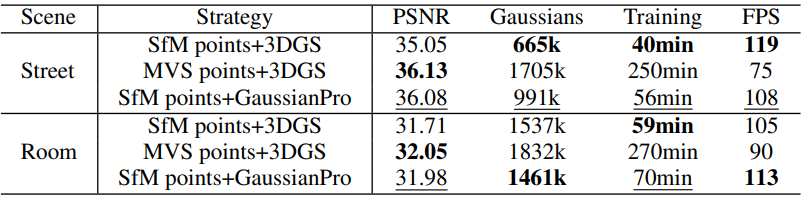
다음은 초기화 전략에 따른 성능과 효율성을 비교한 표이다.