[논문리뷰] Repurposing 2D Diffusion Models with Gaussian Atlas for 3D Generation
ICCV 2025. [Paper] [Page]
Tiange Xiang, Kai Li, Chengjiang Long, Christian Häne, Peihong Guo, Scott Delp, Ehsan Adeli, Li Fei-Fei
Stanford University | Meta Reality Labs
20 Mar 2025
Introduction
본 논문에서는 다양한 object에 대한 고품질 3D Gaussian fitting으로 구성된 대규모 데이터셋인 GaussianVerse를 구축했다. 3D Gaussian 레퍼런스를 미리 계산하는 기존 연구들과 달리, GaussianVerse는 새로운 pruning 전략과 더욱 효율적이지만 계산 집약적인 fitting 프로세스를 통해 최소한의 Gaussian 개수로 더 높은 품질의 fitting 결과를 제공한다.
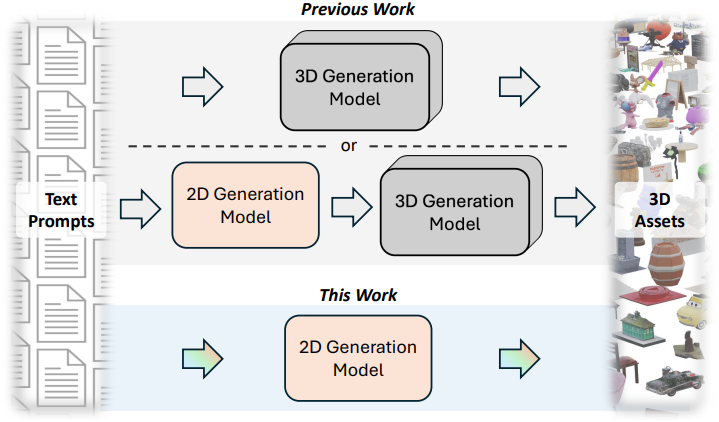
3D 생성을 위한 독립형 diffusion model 설계는 비교적 간단하다. 그러나 이러한 모델은 특히 3D 데이터만으로 학습할 경우 상당한 한계를 지니는데, 이는 고품질 3D 데이터가 2D 이미지에 비해 상대적으로 부족하기 때문이다. 3D 생성에서 더 높은 렌더링 품질을 달성하기 위해서는 잘 사전 학습된 2D diffusion model에서 얻은 prior를 활용하는 것이 바람직하다. 기존 방법들은 복잡한 설계를 통해 가중치가 고정된 사전 학습된 2D diffusion model을 3D 생성 파이프라인에 통합하였다.
본 논문에서는 2D diffusion model을 직접 fine-tuning을 통해 3D 생성에 활용하는 새로운 관점을 제시하였다. 2D diffusion model의 잠재력을 최대한 활용하기 위해, 3D Gaussian을 2D로 표현하는 새로운 방식인 Gaussian Atlas를 도입하였다. 이 표현 방식은 먼저 3D Gaussian을 표준 3D 구면으로 변환한 다음, equirectangular projection을 적용하여 정사각형 2D 그리드로 매핑함으로써 직접 fine-tuning을 가능하게 한다. 이렇게 생성된 Gaussian Atlas는 2D diffusion model에 저장된 prior를 3D 생성에 효과적으로 전달할 수 있다.
GaussianVerse

Diffusion model 학습을 위해서는 다양한 형식의 3D object에 대해 고품질의 3D Gaussian GT를 미리 fitting해야 한다. 본 논문에서는 Scaffold-GS를 기반으로 몇 가지를 수정하여 fitting 모델을 구축했다.
- 뷰 속성 쿼리를 위한 MLP에서 뷰 속성을 제외하여 뷰에 덜 민감한 애플리케이션을 구현할 수 있도록 했다.
- Fitting당 Gaussian 개수를 제한하는 방식을 사용하였다.
다양한 3D object는 각기 다른 geometry와 외형을 가질 수 있으며, 이로 인해 3DGS fitting 결과가 매우 가변적이다. 일반적인 접근 방식은 fitting당 일정한 수의 Gaussian을 사용하는 것인데, 이는 모든 3D object는에 걸쳐 Gaussian 개수가 균일하게 분포되도록 한다. 결과적으로, 폴리곤 수가 적고 단순한 object는 과도하게 parameterize되어, scale과 opacity 값이 낮지만 0은 아닌 값을 가질 수 있다. 본 논문에서는 Gaussian 개수를 일정하게 제한하는 대신, fitting되는 Gaussian 개수를 파라미터 $\tau$로 제한하는 visibility ranking 전략을 도입하였다.
구체적으로, 3DGS fitting 과정에서 각 Gaussian의 opacity를 추적하여 무작위로 선택된 카메라 시점에서의 visibility를 평가한다. Densification 후 Gaussian 개수가 $\tau$를 초과하면, opacity를 기준으로 정렬하고 가장 낮은 값을 가진 Gaussian들을 제거한다. 이 pruning 전략은 완전히 보이지 않는 Gaussian만 제거하는 기존 방식과 다르다. 또한, Scaffold-GS의 디자인과 일관성을 유지하기 위해 앵커의 visibility를 기반으로 동일한 ranking 및 pruning 방식을 적용하였다. 최종적으로 두 가지 visibility의 순위를 평균하여 선택한다.
여러 시점의 RGB 렌더링에 대한 photometric loss들을 최소화함으로써 object별 3D Gaussian을 최적화한다.
\[\begin{equation} \lambda_\textrm{rgb}^\prime \mathcal{L}_\textrm{rgb} + \lambda_\textrm{ssim}^\prime \mathcal{L}_\textrm{ssim} + \lambda_\textrm{lpips}^\prime \mathcal{L}_\textrm{lpips} + \lambda_\textrm{reg}^\prime \mathcal{R} \end{equation}\](\(\mathcal{L}_\textrm{rgb}\)는 color space L1 loss, \(\mathcal{L}_\textrm{ssim}\)은 SSIM loss, \(\mathcal{L}_\textrm{lpips}\)는 perceptual loss, $\mathcal{R}$은 Scaffold-GS의 scale regularization)
Perceptual loss를 추가하면 학습 시간이 거의 두 배로 늘어나지만, 더 적은 Gaussian으로 높은 렌더링 품질을 얻기 위해서는 필수적이다.
데이터셋 디테일
- 총 object 수: 205,737
- 최대 Gaussian 개수: $\tau = 192^2 = 36864$
- 학습 step 수: 20,000
- 각 object당 10분 소요
- 총 3.8 A100 GPU year 소요
Formulating 3D Gaussians as 2D Atlas
Latent Diffusion (LD)은 수십억 쌍의 텍스트-이미지 데이터가 풍부하게 존재하기 때문에 복잡한 자연어를 이해하고 일관성 있는 2D 이미지를 생성할 수 있다. 그러나 텍스트를 3D로 생성하는 데에는 두 가지 주요 이유로 인해 더 큰 어려움이 있다.
- 고품질의 텍스처가 적용된 3D 모델을 생성하고 주석을 다는 작업이 여전히 많은 자원과 시간을 소모하기 때문에 2D 모델과 유사한 수준의 3D 모델을 포함하는 대규모 데이터셋이 부족하다.
- 3D object 표현은 본질적으로 고차원적이므로 복잡한 기하학적 제약 조건을 수반하여 diffusion model이 해석하기 어렵다.
2D와 3D 간의 데이터 가용성 및 표현 복잡성의 이러한 차이는 사전 학습된 2D diffusion model에서 얻은 prior를 3D Gaussian 생성에 활용하는 접근 방식을 제시하도록 하였다.
그러나 3D 공간의 Gaussian은 2D 모델에 직접 전달할 수 없다. 2D 모델은 입력값 $X$가 2차원의 공간 크기만 가져야 하고, dense한 2D 그리드의 각 vertex에 유효한 “픽셀”이 있어야 하며, VAE는 $\textbf{X} \in [-1, 1]$를 만족해야 하고 denoiser는 \(\textbf{X} \sim \mathcal{N}(0, 1)\)를 따르는 값을 가져야 한다는 조건을 요구한다. 3D Gaussian을 2D diffusion model과 호환시키기 위해, 본 논문에서는 3D Gaussian을 2D로 표현한 Gaussian Atlas를 제안하였다.
2D 변환의 간단한 아이디어 중 하나는 3D geometry를 3D 좌표와 주어진 카메라 파라미터를 사용하여 이미지 평면에 projection하는 것이다. 그러나 이러한 방식은 깊이 정보를 완전히 손실하고 원래 3D 구조의 위상 구조를 왜곡한다. 3D 생성은 3D 연속성의 정확한 표현에 의존하기 때문에 위상 구조는 필수적이다. 따라서 3D Gaussian을 2D 평면에 매핑할 뿐만 아니라 3D 연속성을 어느 정도 보존하는 방법이 필요하다.
이러한 요구 사항을 고려할 때, 3D geometry의 표면을 2D 평면에 펼치는 UV texture unwrapping과 유사한 방법이 더 적합하다. 그러나 UV map은 다양한 3D geometry에 대해 신중한 설계가 필요하기 때문에 일반적으로 보편적으로 적용할 수 없다. 따라서 저자들은 3D geometry와 2D UV 사이의 정확한 매핑 대신, UV unwrapping의 한 가지 특징인 geometry flattening에 초점을 맞추었다.
구체적으로, 본 논문의 목표는 3D Gaussian의 3D 위치 \(\{\textbf{x} \in \mathbb{R}^3\}\)를 2D 평면 좌표 \(\{\hat{\textbf{x}} \in \mathbb{R}^2\}\)로 변환하는 매핑 함수 $\mathcal{M}(\cdot)$을 찾는 것이다. 이러한 함수 $\mathcal{M}$을 신경망으로 parameterize하여 최적화하는 방식은 서로 다른 object에 대해 $\mathcal{M}$을 반복적으로 학습시켜야 하므로 시간이 많이 소요될 뿐만 아니라, 2D flattening에 대한 휴리스틱이 object마다 다를 수 있어 매핑 과정의 일관성이 떨어진다. 결과적으로 diffusion model은 불규칙한 패턴을 포착하지 못하고 의미 있는 콘텐츠를 생성하지 못한다. 따라서 본 논문에서는 간단하고 deterministic한 매핑 함수를 사용하여 3D와 2D 간의 보다 일관된 변환을 추구하였다.
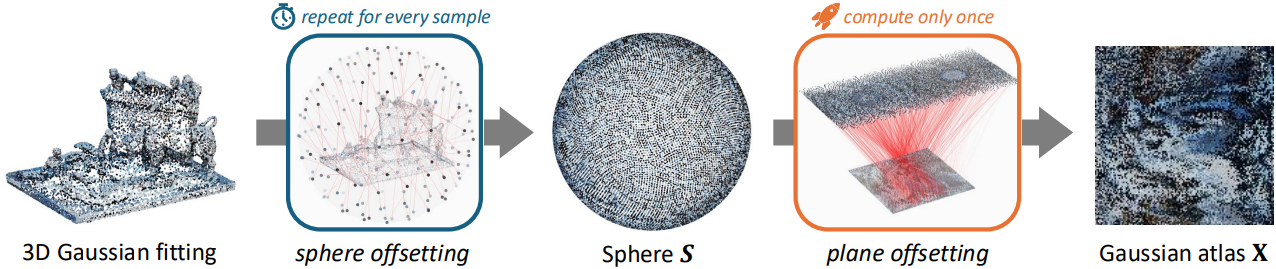
변환 과정은 세 단계로 구성된다. 첫 번째 단계에서는 3D 축의 원점을 중심으로 하고 반지름이 1인 단위 구 $\mathcal{S}$를 가정하고, 그 표면에 균일하게 분포된 $N$개의 3D 점 \(\{\textbf{s}_i \in \mathbb{R}^3\}\)으로 표현한다. 구는 2D projection에 대한 다양한 표준을 제공하는 잘 연구된 구조이므로 flattening 과정에 적합하다. 그런 다음, Optimal Transport (OT)를 사용하여 3D Gaussian들을 구 $\mathcal{S}$의 표면 점 \(\{s_i \in \mathbb{R}^3\}\)으로 이동시킨다. 이 과정을 sphere offsetting이라고 부른다.
3D Gaussian을 단위 구의 표면에 배치한 후, equirectangular projection을 매핑 함수 $\mathcal{M}$으로 사용하여 3D Gaussian의 flattening된 2D 좌표 \(\{p_i \in \mathbb{R}^2\}\)를 얻는다. 마지막으로, plane offsetting 단계에서 또 다른 OT를 적용하여 \(\{p_i\}\)를 공간 크기가 $\sqrt{N} \times \sqrt{N}$인 정사각형 2D 그리드의 꼭짓점 \(\{q_i \in \mathbb{R}^2\}\)에 매핑함으로써 sparsity를 더욱 줄인다. 특히, $\mathcal{M}$이 deterministic한 함수이므로 \(\{p_i\}\)와 \(\{q_i\}\) 사이의 매핑은 모든 object에 대해 동일하게 유지된다. 이러한 일관성 덕분에 마지막 단계에서 변환을 한 번만 수행하고 계산된 인덱스를 모든 object에 재사용할 수 있다.
3D Gaussian의 최종 격자형 2D 표현을 Gaussian Atlas라고 부르며, 각 atlas $\textbf{X}$는
\[\begin{equation} \sqrt{N} \times \sqrt{N} \times (\| \textbf{x} - \textbf{x} \| + \| \textbf{c} \| + \| \textbf{o} \| + \| \textbf{s} \| + \| \textbf{r} \|) \end{equation}\]의 shape으로 3D Gaussian의 모든 속성을 포함한다.
2D Diffusion for 3D Gaussian Generation
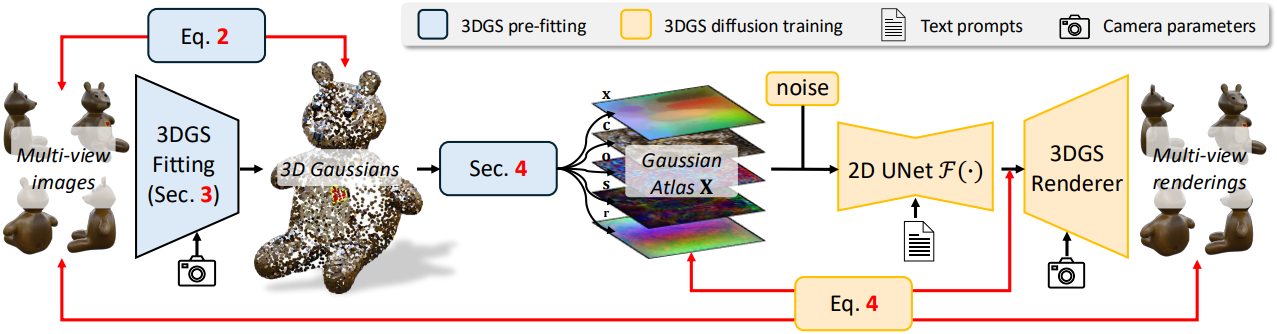
3D Gaussian을 2D 평면으로 변환한 후, 사전 학습된 Latent Diffusion 모델을 Gaussian Atlas를 사용하여 fine-tuning할 수 있다.
LD의 표준 fine-tuning 방식은 VAE 기반 인코딩 및 디코딩을 포함한다. 그러나 Gaussian 속성은 LD 학습에 사용된 이미지의 속성과 다르기 때문에 이러한 오토인코딩이 Gaussian Atlas에는 적합하지 않다. 2D atlas를 사용하여 LD UNet을 fine-tuning하는 것은 atlas의 분포가 VAE로 인코딩된 latent의 분포와 일치하는 경우에만 가능하다.
따라서 저자들은 전체 GaussianVerse에서 계산된 픽셀별 평균과 표준 편차를 사용하여 2D atlas를 표준화하였다. 이러한 정규화는 극단적으로 높거나 낮은 주파수의 픽셀 값을 방지하는 동시에 원래 VAE로 인코딩된 이미지 latent의 특성을 보존하여 궁극적으로 fine-tuning 프로세스를 가속화한다.
3D Gaussian은 3D 위치 $\textbf{x} \in \mathbb{R}^3$, albedo $\textbf{c} \in \mathbb{R}^3$, scale $\textbf{s} \in \mathbb{R}^3$, opacity $\textbf{o} \in \mathbb{R}$, $\textbf{r} \in \mathbb{R}^4$의 다섯 가지 속성으로 특징지어진다. LD UNet은 원래 4채널 latent를 사용하여 학습되었으므로, 각 3채널 속성에 1채널 opacity를 추가하고 UNet의 입력 레이어를 네 번 반복하여 모든 속성을 입력으로 사용한다. UNet의 fine-tuning에 사용되는 최종 Gaussian Atlas는 크기가 128$\times$128$\times$16이다. 렌더링 과정에서 각 속성을 적절히 unpack하고 세 opacity 값을 평균화한다.
Denoising된 Gaussian의 렌더링 결과와 레퍼런스 이미지 간의 diffusion loss와 perceptual loss를 조합하여 LD UNet $F$를 fine-tuning한다.
\[\begin{equation} \lambda_\textrm{diff} \mathcal{L}_\textrm{diff} + \lambda_\textrm{rgb} \mathcal{L}_\textrm{rgb} + \lambda_\textrm{mask} \mathcal{L}_\textrm{mask} + \lambda_\textrm{lpips} \mathcal{L}_\textrm{lpips} \\ \mathcal{L}_\textrm{diff} = \mathbb{E}_{l_0, \textbf{z}, t} \left[ \| \nabla_{l_t} \textbf{z} - \nabla_{l_t} \mathcal{F} (l_t, t) \|^2 \right] \end{equation}\](\(\mathcal{L}_\textrm{mask}\)는 렌더링된 opacity map에 대하 L1 loss)
Experiments
- 구현 디테일
- $\tau$ = 36,864
- $N$ = 16,384 = 128$\times$128
- classifier-free guidance 적용 (20% 확률로 텍스트 인코딩을 0으로)
- optimizer: AdamW
- learning rate: $5 \times 10^{-5}$
- batch size: 64
- step: 100만
- 학습에 EMA, mixed precision 적용
- GPU: A100 8개
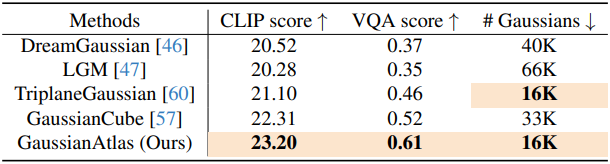
다음은 여러 3D 생성 모델과의 비교 결과이다.

다음은 Gaussian Atlas의 생성 예시들이다.

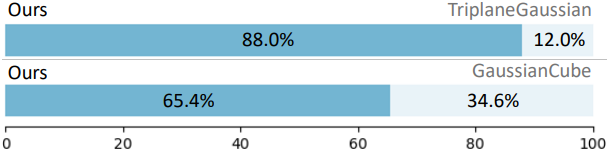
다음은 user study 결과이다.
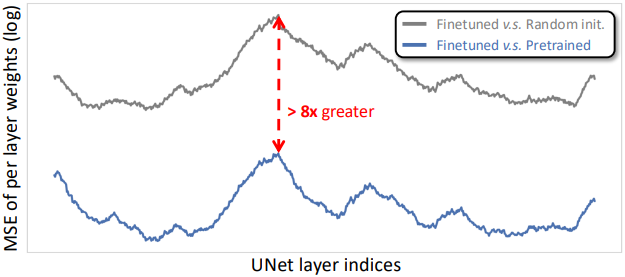
다음은 사전 학습된 diffusion model에서 fine-tuning할 때와 처음부터 학습할 때의 결과를 비교한 것이다.

다음은 두 object(a)에 대하여 본 논문의 flattening 방식(b)과 최적화 기반 방식(c)으로 얻은 atlas (3D 위치 $\textbf{x}$)이다. (d)와 (e)는 각각 최적화 기반 방식으로 학습된 모델이 생성한 Gaussian과 atlas이다.

다음은 fine-tuning된 UNet과 랜덤 초기화된 UNet, 그리고 사전 학습된 UNet 간의 가중치 차이를 그래프로 나타낸 것이다.