[논문리뷰] FSGS: Real-Time Few-shot View Synthesis using Gaussian Splatting

ECCV 2024. [Paper] [Page] [Github]
Zehao Zhu, Zhiwen Fan, Yifan Jiang, Zhangyang Wang
University of Texas at Austin
1 Dec 2023

Introduction

3D Gaussian Splatter (3D-GS)는 최근 밀집된 카메라 시점 모음에서 3D 장면을 모델링하는 효율적인 표현으로 등장했다. 복잡한 모양과 외관을 모델링하기 위한 속성을 갖춘 3D Gaussian의 조합으로 장면을 표현하고, splatting 기반 rasterization을 통해 2D 이미지를 렌더링한다. 볼륨 렌더링을 효율적인 미분 가능한 splatting으로 대체함으로써 3D Gaussian Splatting은 새로운 시점에서 사실적인 이미지를 렌더링하는 능력을 유지하면서 실시간 렌더링 속도를 달성하였다. 그러나 3D-GS는 Structure-fromMotion (SfM) 포인트에서 초기화되며 성능은 초기화된 포인트의 수량과 정확성에 크게 좌우된다. 이후의 Gaussian densification은 under-reconstruction된 영역과 over-reconstruction된 영역 모두에서 Gaussian 수를 증가시킬 수 있지만 이 간단한 전략은 few-shot 설정에서는 부족하다. 초기화가 부족하여 결과가 oversmoothing되고 학습 뷰에 과적합(overfit)되는 경향이 있다.

본 논문의 목표는 제한된 관찰로부터 시각적 충실도를 유지하면서 간결하고 효율적인 표현을 구성하는 것이다. 이를 위해 저자들은 3D Gaussian을 표현으로 사용하여 sparse한 시점 입력에서 대규모 장면을 모델링하는 FSGS를 제시하였다.

Sparse한 입력과 dense한 coverage의 격차를 완화하는 문제를 해결하기 위한 첫 번째 과제는 3D 장면을 덮고 표현하기 위해 Gaussian의 위치를 효과적으로 이동하는 방법이다. 따라서 저자들은 기존 Gaussian과 이웃의 근접성(proximity)을 측정하여 새로운 Gaussian을 성장시키는 Proximity-guided Gaussian Unpooling을 제안하였다. 새로운 Gaussian을 가장 대표적인 위치에 배치하고 기존 Gaussian의 정보로 초기화함으로써 포괄적인 장면 적용을 위해 Gaussian 수를 효과적으로 늘린다.

다음 과제는 멀티뷰 큐가 충분하지 않은 경우에도 성장한 Gaussian이 장면의 기하학적 구조를 올바르게 표현하도록 하는 방법이다. 따라서 새로운 Gaussian의 최적화를 제어하고 정규화하려면 추가 prior를 활용하는 것이 필수적이다. 구체적으로, 저자들은 사전 학습된 monocular depth estimator를 학습 뷰와 증강된 pseudo-view 모두에서 사용하여 풍부한 depth prior를 활용하는 것을 제안하였다. 이는 Gaussian Unpooling이 합리적인 해로 수렴하고 장면의 기하학적 매끄러움을 보장하도록 가이드한다. 통합된 depth prior의 역전파는 미분 가능한 depth rasterizer를 구현하여 달성된다.

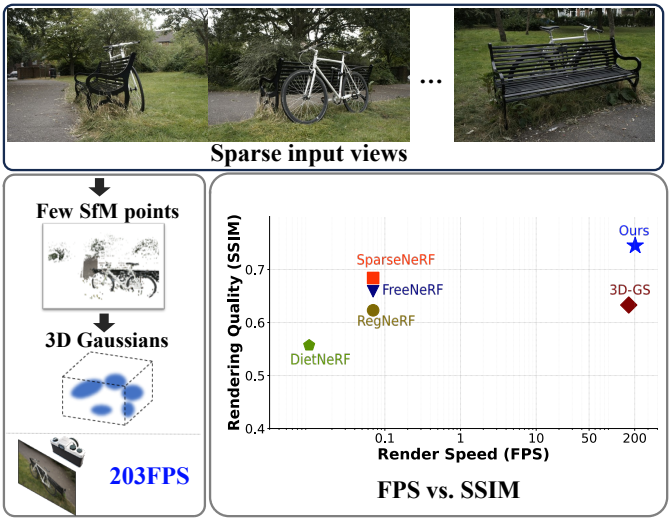
FSGS는 SOTA 렌더링 품질을 달성하는 동시에 실제 렌더링에 실용적인 속도인 203FPS에서 실행될 수 있다.

Method

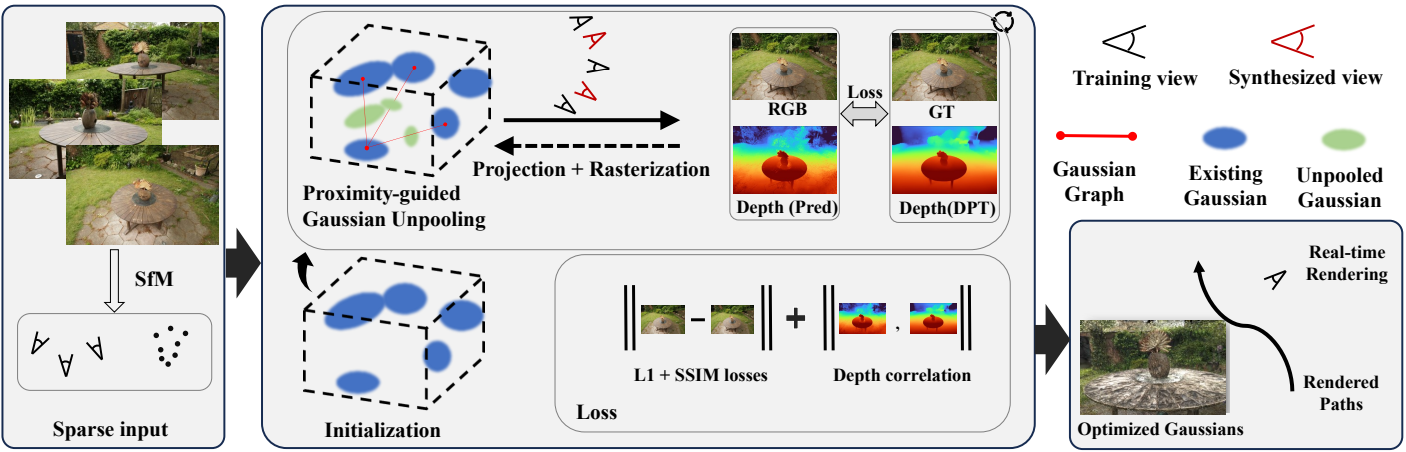
FSGS 프레임워크의 개요는 위 그림에 나와 있다. FSGS는 정적인 장면 내에서 캡처된 제한된 수의 이미지를 입력받는다. 카메라 포즈와 sparse한 포인트 클라우드는 Structure-from-Motion(SfM)에서 계산된다. 추가 학습에 사용되는 초기 3D Gaussian은 색상, 위치, 모양 속성을 사용하여 SfM 포인트에서 초기화된다. 극도로 sparse한 SfM 포인트와 불충분한 관측 문제는 Proximity-guided Gaussian Unpooling을 채택하여 Gaussian의 밀도를 높이고 기존 Gaussian 간의 근접성(proximity)을 측정하고 새 Gaussian을 가장 대표적인 위치에 전략적으로 배치하여 빈 공간을 채워 디테일 처리 용량을 증가시킴으로써 해결된다. Densify된 Gaussian이 올바른 장면 형상에 맞게 최적화될 수 있도록 보장하기 위해 2D depth estimator의 prior를 활용한다.

1. Preliminary and Problem Formulation

3D Gaussian Splatting(3D-GS)은 위치 벡터 $\boldsymbol{\mu} \in \mathbb{R}^3$과 공분산 행렬 $\Sigma \in \mathbb{R}^{3 \times 3}$을 사용하여 3D Gaussian 컬렉션을 통해 명시적으로 3D 장면을 나타낸다. 각 Gaussian은 3D Gaussian 분포에 따라 3D 공간의 점 $\mathbf{x}$에 영향을 미친다.

\[\begin{equation} G(\mathbf{x}) = \frac{1}{(2\pi)^{3/2} \vert \Sigma \vert^{1/2}} e^{-\frac{1}{2} (\mathbf{x} - \boldsymbol{\mu})^\top \Sigma^{-1} (\mathbf{x} - \boldsymbol{\mu})} \end{equation}\]

Σ가 positive semi-definite이고 실질적인 물리적 중요성을 유지하는지 확인하기 위해 $\Sigma$는 $\Sigma = RSS^\top R^\top$에 의해 두 개의 학습 가능한 성분으로 분해된다. 여기서 $R$은 회전을 나타내는 quaternion matrix이고 $S$는 scaling matrix이다.

또한, 각 가우시안은 불투명도(opacity) logit $o \in \mathbb{R}$과 $n$개의 spherical harmonic(SH) 계수 \(\{c_i \in \mathbb{R}^3 \vert i = 1, 2, \ldots, n\}\)으로 표시되는 외형 feature를 저장한다. 여기서 $n = D^2$은 degree가 $D$인 SH의 계수의 개수이다. 2D 이미지를 렌더링하기 위해 3D-GS는 픽셀에 기여하는 모든 Gaussian을 정렬하고 다음 함수를 사용하여 픽셀과 겹치는 정렬된 Gaussian을 혼합한다.

\[\begin{equation} c = \sum_{i=1} c_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]

여기서 $c_i$는 $i$번째 Gaussian의 SH 계수에서 계산된 색상이다. $\alpha_i$는 공분산 $\Sigma^\prime \in \mathbb{R}^{2 \times 2}$에 불투명도를 곱한 2D Gaussian을 평가하여 제공된다. 2D 공분산 행렬 $\Sigma^\prime$는 $\Sigma^\prime = JW \Sigma W^\top J^\top$로 계산되며 3D 공분산 $\Sigma$를 카메라 좌표에 투영한다. 여기서 $J$는 projection transformation의 affine 근사의 Jacobian을 나타내고, $W$는 view transformation 행렬이다.

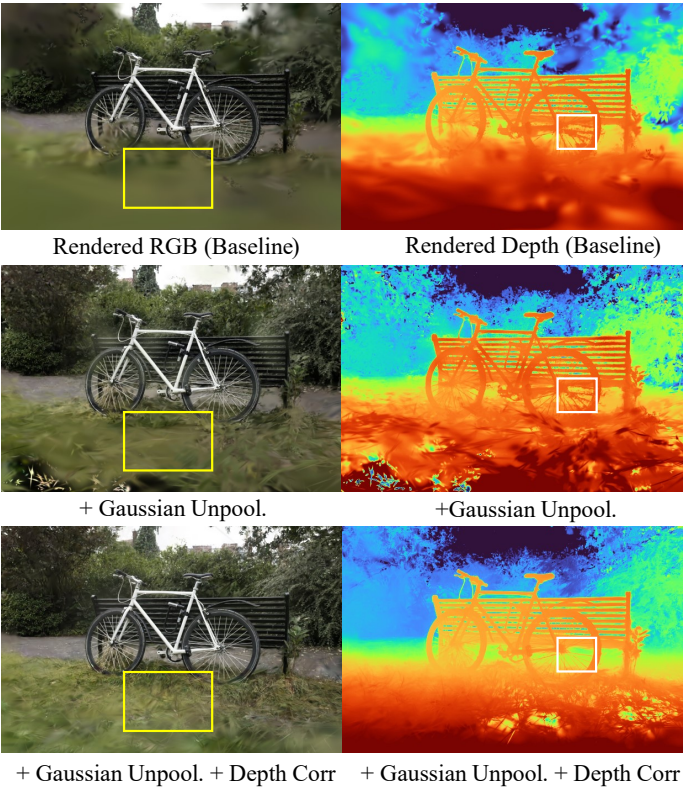
3D-GS에는 휴리스틱한 Gaussian densification 체계가 도입되었다. 여기서 Gaussian은 임계값을 초과하는 view-space 위치 기울기의 평균 크기를 기반으로 densify된다. 이 방법은 포괄적인 SfM 포인트로 초기화할 때 효과적이지만 sparse한 뷰 입력 이미지에서 극도로 sparse한 포인트 클라우드로 전체 장면을 완전히 덮는 데는 충분하지 않다. 또한 일부 Gaussian은 극도로 큰 볼륨으로 성장하는 경향이 있어 학습 뷰에 overfit되고 새로운 뷰에 잘못 일반화되는 결과로 이어진다. (아래 그림 참조)

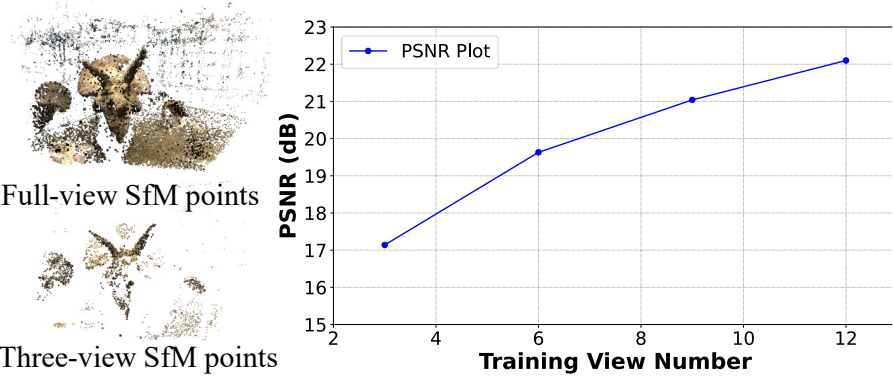
2. Proximity-guided Gaussian Unpooling

모델링된 장면의 세분성은 장면을 나타내는 3D Gaussian의 품질에 크게 좌우된다. 따라서 제한된 3D 장면 범위를 해결하는 것은 효과적인 sparse 뷰 모델링에 중요하다.

Proximity Score and Graph Construction

Gaussian 최적화 동안 유클리드 거리를 계산하여 기존의 각 Gaussian을 $K$개의 nearest neighbors와 연결하기 위해 근접 그래프(proximity graph)라고 하는 방향 그래프를 구성한다. 머리에 있는 Gaussian을 “source” Gaussian으로 표시하고, 꼬리에 있는 Gaussian을 source의 $K$ neighbors 중 하나인 “destination” Gaussian으로 표시한다. 각 Gaussian에 할당된 근접성(proximity) 점수는 $K$개의 nearest neighbors까지의 평균 거리로 계산된다. 근접 그래프는 최적화 중 densification 또는 pruning 프로세스에 따라 업데이트된다. 실제로 저자들은 $K$를 3으로 설정했다.

Gaussian Unpooling

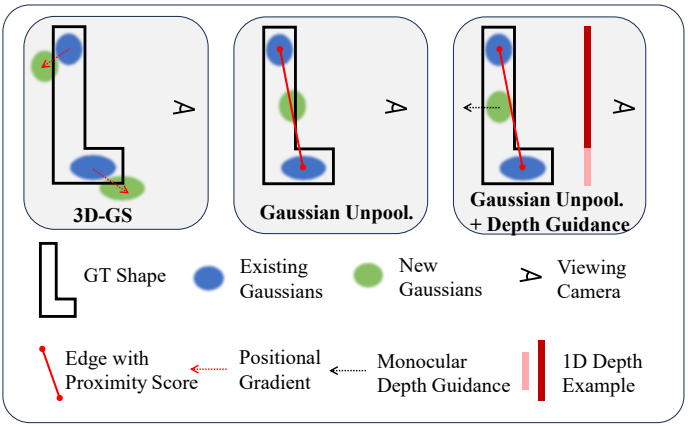
저자들은 컴퓨터 그래픽에서 널리 사용되는 메시 분할 알고리즘의 vertex-adding 전략에서 영감을 받아 근접 그래프와 각 Gaussian의 근접 점수를 기반으로 Gaussian Unpooling을 제안하였다. 구체적으로, Gaussian의 근접성 점수가 threshold $t_\textrm{prox}$를 초과하는 경우, 위 그림과 같이 “source” Gaussian과 “destination” Gaussian을 연결하여 각 정점의 중심에 새로운 Gaussian을 성장시킨다. 새로 생성된 Gaussian의 불투명도는 “destination” Gaussian의 불투명도와 일치하도록 설정된다. 한편, rotation과 SH 계수와 같은 다른 속성은 0으로 초기화된다. Gaussian Unpooling 전략은 새로 densify된 Gaussian이 가장 대표적인 위치 주위에 분산되도록 장려하고 최적화 중에 관측 공백을 점진적으로 메운다.

3. Geometry Guidance for Gaussian Optimization

Gaussian Unpooling으로 dense한 coverage를 달성한 후 멀티뷰 단서가 있는 photometric loss가 Gaussian 최적화에 적용된다. 그러나 sparse 뷰 설정에서 관찰이 충분하지 않으면 일관된 형상을 학습하는 능력이 제한되어 학습 뷰에 overfit이 발생할 위험이 높고 새로운 뷰에 대한 일반화가 좋지 않다. 이를 위해서는 Gaussian 최적화를 가이드하기 위해 추가 정규화나 prior를 통합해야 한다. 특히, Gaussian의 형상을 합리적인 해로 가이드하기 위해 잘 학습된 monocular depth estimator에 의해 생성된 depth prior로부터 도움을 구한다.

Injecting Geometry Coherence from Monocular Depth

저자들은 140만 개의 이미지-깊이 쌍으로 사전 학습된 Dense Prediction Transformer(DPT)를 사용하여 학습 뷰에서 깊이 맵 $D_\textrm{est}$를 생성하였다. 실제 장면 스케일과 추정된 깊이 사이의 스케일 모호성을 완화하기 위해 추정된 깊이 맵과 렌더링된 깊이 맵에 Pearson correlation을 도입하였다. Pearson correlation은 2D 깊이 맵 사이의 분포 차이를 측정하고 아래 함수를 따른다.

\[\begin{equation} \textrm{Corr} (\mathbf{D}_\textrm{ras}, \mathbf{D}_\textrm{est}) = \frac{\textrm{Cov}(\mathbf{D}_\textrm{ras}, \mathbf{D}_\textrm{est})}{\sqrt{\textrm{Var}(\mathbf{D}_\textrm{ras}) \textrm{Var}(\mathbf{D}_\textrm{est})}} \end{equation}\]

이 소프트한 제약 조건을 사용하면 절대적인 깊이 값의 불일치에 방해받지 않고 깊이 구조를 정렬할 수 있다.

Differentiable Depth Rasterization

Gaussian 학습을 가이드하기 전에 깊이로부터의 역전파를 가능하게 하기 위해 저자들은 미분 가능한 depth rasterizer를 구현하여 렌더링된 깊이 $D_\textrm{ras}$와 추정된 깊이 $D_\textrm{est}$ 사이의 오차 신호를 수신할 수 있도록 하였다. 특히 depth rasterization을 위해 3D-GS의 알파 블렌딩 렌더링을 활용하였다. 여기서 픽셀에 기여하는 정렬된 Gaussian의 $z$-버퍼가 깊이 값을 생성하기 위해 누적된다.

\[\begin{equation} d = \sum_{i=1}^n d_i \alpha_i \prod_{j=1}^{i-1} (1 - \alpha_j) \end{equation}\]

여기서 $d_i$는 $i$번째 Gaussian의 $z$-버퍼를 나타낸다. 완전 미분 가능한 구현을 통해 깊이 correlation loss가 가능해 렌더링된 깊이와 추정된 깊이 간의 유사성이 더욱 향상된다.

Synthesize Pseudo Views

Sparse한 학습 뷰에 대한 overfitting의 고유한 문제를 해결하기 위해 저자들은 관찰되지 않은 뷰(pseudo-view)에 대한 augmentation을 사용하여 2D prior 모델에서 파생된 장면 내에 더 많은 prior를 통합한다. 합성된 뷰는 유클리드 공간에서 가장 가까운 두 학습 뷰에서 샘플링되어 평균 카메라 방향을 계산하고 그 사이에 가상 방향을 보간한다. 3DoF 카메라 위치에는 다음 식과 같이 랜덤한 노이즈가 적용되며, 그런 다음 이미지가 렌더링된다.

\[\begin{equation} \mathbf{P}^\prime = (\mathbf{t} + \epsilon, \mathbf{q}), \quad \epsilon \sim \mathcal{N}(0, \delta) \end{equation}\]

여기서 $\mathbf{t} \in \mathbf{P}$는 카메라 위치를 나타내고, $q$는 두 카메라의 평균 회전을 나타내는 quaternion이다. 온라인 pseudo-view들을 합성하는 이러한 접근 방식은 3D Gaussian이 점진적으로 업데이트되므로 동적인 형상 업데이트를 가능하게 하여 overfitting 위험을 줄인다.

4. Optimization

전부 결합하면 학습 loss \(\mathcal{L}(\mathbf{G}, \mathbf{C})\)는 다음과 같다.

\[\begin{aligned} \mathcal{L}(\mathbf{G}, \mathbf{C}) &= \lambda_1 \mathcal{L}_1 + \lambda_2 \mathcal{L}_\textrm{ssim} + \lambda_3 \mathcal{L}_\textrm{prior} \\ \mathcal{L}_1 &= \| \mathbf{C} - \hat{\mathbf{C}} \|_1 \\ \mathcal{L}_\textrm{ssim} &= \textrm{D-SSIM}(\mathbf{C}, \hat{\mathbf{C}}) \\ \mathcal{L}_\textrm{prior} &= \textrm{Corr}(\mathbf{D}_\textrm{ras}, \mathbf{D}_\textrm{est}) \end{aligned}\]

여기서 \(\mathcal{L}_1\)과 \(\mathcal{L}_\textrm{ssim}\)은 예측 이미지 $\hat{\mathbf{C}}$와 실제 이미지 $\mathbf{C}$ 사이의 photometric loss 항이다. \(\mathcal{L}_\textrm{prior}\)는 학습 뷰와 합성된 pseudo-view에 대한 기하학적 정규화 항이다. 저자들은 grid search를 통해 \(\lambda_1\), \(\lambda_2\), \(\lambda_3\)을 각각 0.8, 0.2, 0.05로 설정했다. Pseudo-view 샘플링은 2,000번의 iteration 후에 활성화되어 Gaussian이 장면을 대략적으로 표현할 수 있도록 한다.

FSGS의 학습 알고리즘은 Algorithm 1과 같다.

Experiments

• 데이터셋
  • LLFF: 학습 뷰 3개 사용
  • Mip-NeRF360: 학습 뷰 24개 사용
  • Blender: 학습 뷰 8개 사용 (테스트 시 25개)
• 구현 디테일
  • SfM으로 초기 카메라 포즈와 포인트 클라우드 계산
  • 100 iteration마다 Gaussian을 densify (500 iteration 이후에)
  • 전체 최적화 step: 10,000
  • $t_\textrm{prox} = 10$
  • 2,000 iteration 이후에 pseudo-view가 샘플링됨 ($\sigma = 0.1$)
  • GPU: NVIDIA A6000

1. Comparisons to other Few-shot Methods

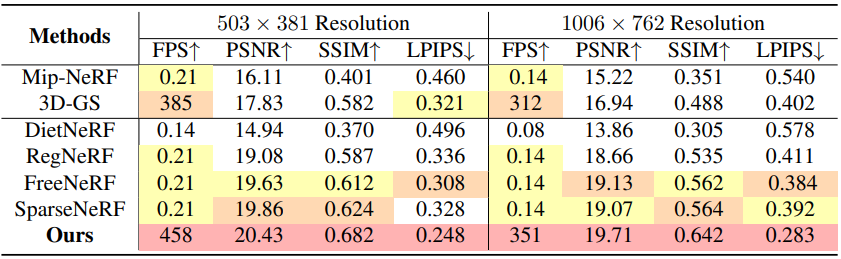
다음은 LLFF 데이터셋에서의 결과를 비교한 것이다.

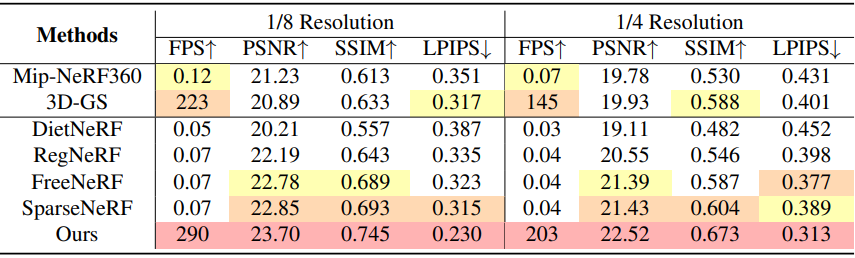
다음은 Mip-NeRF360 데이터셋에서의 결과를 비교한 것이다.

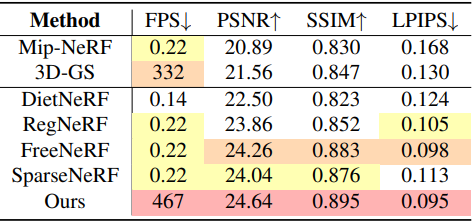
다음은 Blender 데이터셋에서의 결과를 비교한 것이다.

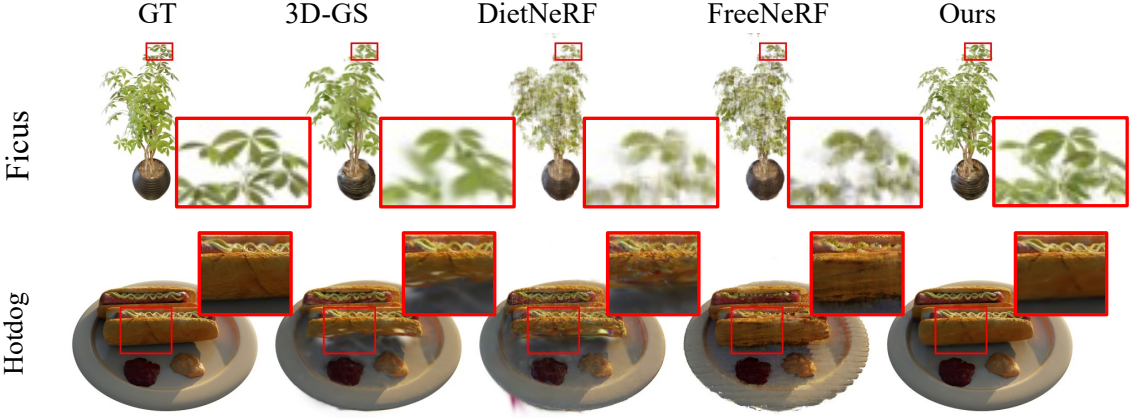
2. Ablation Studies

다음은 ablation study 결과이다.

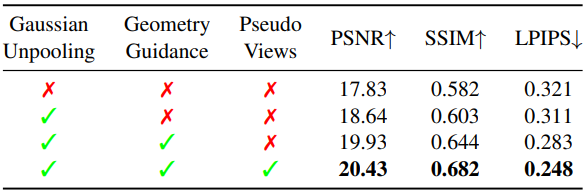
다음은 ablation study 결과를 시각화 한 것이다.