[논문리뷰] Few-Shot Diffusion Models
arXiv 2022. [Paper]
Giorgio Giannone, Didrik Nielsen, Ole Winther
Technical University of Denmark | Norwegian Computing Center | University of Copenhagen
30 May 2022
Introduction
인간은 한 번도 본 적이 없는 사물의 개념과 기능을 파악할 수 있는 예외적인 few-shot 학습자이다. 이는 우리가 세계의 내부 모델을 구축하여 물체의 모양과 기능에 대한 사전 지식을 결합하여 아주 적은 데이터에서 잘 학습된 추론을 할 수 있기 때문이다. 대조적으로, 전통적인 기계 학습 시스템은 백지 상태에서 학습되어야 하므로 훨씬 더 많은 데이터가 필요하다.
특히 생성 모델의 few-shot adaptation은 어려운 문제다. Few-shot 생성은 손으로 만든 aggregation 및 컨디셔닝 메커니즘을 사용하여 간단한 데이터셋과 얕은 task로 제한되었다.
이미지와 같은 고차원의 복잡한 데이터 양식을 위한 생성 모델은 기계 학습의 과제였다. 대형 비전 모델과 대형 언어 모델은 구조화되지 않은 데이터를 처리하는 능력을 크게 향상시켜 multimodal하고 의미론적인 생성의 문을 열었다.
최근 diffusion model은 다양한 분야에서 인상적인 생성 성능을 보여 일반적이고 안정적인 순수 생성 모델을 향한 중요한 발전을 이루었다. Unconditional diffusion model은 샘플의 품질이 높고 표현력 있는 likelihood 기반 밀도 추정기이다. 이러한 표현력은 forward process의 특수한 구조 (각 step의 posterior를 closed form으로 파라미터 없이 계산 가능) 덕분에 학습 중에 수행할 수 있는 Monte Carlo 샘플링에서 발생한다.
그러나 이러한 효과는 posterior의 유연성과 latent space 구조의 부재를 일으킨다. 이러한 이유로 diffusion model의 few-shot capacity는 대부분 탐구되지 않았으며 조건부 적응이 어렵다.
컨디셔닝 메커니즘은 테스트 적응, low-shot 속성 생성, 클래스 정보를 위해 제안되었지만 복잡하고 새로운 클래스 또는 학습 중에 결코 만나지 않는 객체를 생성하지 않는다. 복잡하고 새로운 객체를 다룰 때 간단한 컨디셔닝 메커니즘이 실패하므로 few-shot 생성을 위한 보다 표현적인 접근 방식이 필요하다.
본 논문에서 적응 메커니즘을 연구하고 현실적이고 복잡한 시각적 데이터에 대한 few-shot 생성을 개선하는 것을 목표로 한다.

저자들이 고려한 것은 대량의 동종 세트에서 학습하는 것이며, 각 세트가 하나의 클래스의 샘플들이 정렬되지 않은 모음이다. 테스트 시 모델은 학습 중에 접하지 않은 클래스들의 세트를 제공받는다. 저자들은 전역 변수가 주어진 세트에 대한 정보를 전달하는 계층적으로 이루어진 컨디셔닝을 고려하였다. 조건부 계층 모델은 각각 다른 컨디셔닝 세트 레벨의 변수로 지정된 생성 모델을 자연스럽게 나타낼 수 있다. FSDM은 ViT와 diffusion model을 사용한다. 패치에서 입력 세트를 처리하고 입력 세트에 대해 토큰화된 표현을 사용하여 학습 가능한 attention 메커니즘으로 생성 모델을 컨디셔닝할 것을 제안한다.
본 논문의 기여는 다음과 같다.
- DDPM 프레임워크에서 사실적인 이미지 세트에 대해 few-shot 생성을 수행하는 새로운 프레임워크
- Learnable Attentive Conditioning (LAC): 입력 세트가 패치 모음으로 처리되고 샘플 레벨의 변수와 세트 레벨의 변수 간의 attention을 통해 DDPM을 조절하는 데 사용되는 컨디셔닝 메커니즘
- 모델이 관련 unconditional 및 conditional DDPM 기반의 baseline과 비교하여 학습 속도를 높이고 샘플 품질과 다양성을 높이며 조건부 및 few-shot 생성을 위한 transfer를 개선한다는 실험적 증거
Few-Shot Diffusion Models
본 논문의 목표는 빠르게 적응하는 새로운 생성 task를 학습하는 것이다. 즉, 보지 못한 샘플들을 포함하는 세트 $X$를 조건으로 하는 few-shot 생성을 수행하고자 한다. 저자들은 이를 위해 diffusion model $p_\theta(x \vert X)$를 학습시킨다. 이 접근법을 Few-Shot Diffusion Models (FSDM)이라 부른다.
모델은 아래 그림과 같이 2개의 주요 부분으로 나눌 수 있다.

- $X$의 컨텍스트 표현 $c = h_\phi (X)$를 생성하는 신경망 $h_\phi$
- 새로운 샘플을 $c$를 조건으로 생성하는 conditional diffusion model
Generative Model
생성 모델은 context net $h_\phi$로 생성된 컨텍스트 $c$로 $X$를 컨디셔닝한 conditional diffusion model이다.
\[\begin{equation} p_\theta (x_{0:T} \vert X) = p_\theta (x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t, c), \quad c = h_\phi (X) \end{equation}\]본 논문에서는 $h_\phi$로 Vision Transformer (ViT)를 사용하며, UNet 인코더도 실험한다. Diffusion model $p_\theta (x_{t-1} \vert x_t, c)$는 일반적으로 사용하는 UNet을 사용한다. 추가 컨텍스트 $c$가 있기 때문에 $x_t$의 정보와 $c$를 융합하여 $x_{t-1}$을 사용하는 UNet이어야 한다. 이를 위해 2가지 주요 메커니즘을 사용한다.
- FiLM 기반의 메커니즘
- Learnable Attentive Conditioning (LAC)
Prior도 $c$로 컨디셔닝할 수 있지만 ($p_\theta (x_T \vert c)$), 단순화를 위해 표준 unconditional Gaussian $p_\theta (x_T) = \mathcal{N} (0,I)$을 사용한다.
Inference Model
DDPM의 특별한 구조와 FSDM이 주어지면, inference 모델은 파라미터가 필요 없고 $c$로 컨디셔닝할 필요도 없다. FSDM은 각 step에서 noise를 더해 정보를 손상시키는 diffusion parameter-free posterior를 사용한다.
Loss and Training
Negative ELBO는 conditional 버전으로 표현될 수 있다.
\[\begin{equation} L_\textrm{FSDM} = L_0^c + \sum_{t=2}^T L_{t-1}^c + L_T^c \end{equation}\]일반적인 DDPM들과 마찬가지로 loss는 독립적으로 계산할 수 있는 layer당 하나의 항의 합으로 분해할 수 있다. 따라서 학습은 몬테카를로 샘플링 항으로 목적 함수의 효율적인 확률적 추정을 얻을 수 있는 동일한 이점을 가지고 있다. Conditional per-layer loss $L_{t-1}^c$는 다음과 같다.
\[\begin{equation} L_{t-1, \epsilon}^c = \mathbb{E}_{q(\epsilon)} [\| \epsilon_\theta (x_t, c) - \epsilon \|_2^2], \quad x_t (x_0, \epsilon) = \sqrt{\vphantom{1} \bar{\alpha}_t} x_0 + \sqrt{1 - \bar{\alpha}_t} \epsilon \end{equation}\]$L_T^c$는 unconditional하고 고정된며, $L_0^c$는 negated conditional discretized normal likelihood이다.
\[\begin{equation} L_0^c = \mathbb{E}_q(x_1 \vert x_0) [-\log p_\theta (x_0 \vert x_1, c)] \end{equation}\]Context net은 입력 샘플 $x$와 레이블을 공유하는 작은 세트 $X$에서 정보를 추출한다. 일반적으로 학습 중에 컨텍스트는 입력에 의존하거나 ($x \in X$) 입력에 독립적일 수 있다 ($x \notin X$). 입력에 의존하는 경우 $X$가 주어질 때 각각의 새로운 입력 $x$에 대해 다른 컨텍스트 aggregation을 배울 수 있다. 입력에 독립적인 경우 $X$가 주어질 때 모든 $x$에 대해 컨텍스트 aggregation이 같다.
저자들은 두 경우 모두에 대하여 학습에 사용해 보았으며, 입력에 독립적인 경우가 in-distribution에서 조금 더 성능이 좋고 out-distribution에서 성능이 떨어진다고 한다. 이는 컨디셔닝 메커니즘이 테스트에 잘못된 정보를 사용한다는 것을 의미한다. 반대로 입력에 의존하는 경우, out-distribution에서 컨디셔닝 품질이 좋았으며 in-distribution에서 샘플의 다양성이 나빠진다고 한다. 이러한 발견을 바탕으로 저자들은 입력에 의존하는 방법을 사용하였으며 aggregation 메커니즘이 bottleneck에서 작동한다. 테스트 시 conditional 및 few-shot 샘플링은 일반적인 in-distribution 또는 out-distribution의 세트에서 수행된다.
1. ViT as Set Encoder
Transformer는 사실상 NLP와 텍스트 생성의 표준 모델이다. 최근 ViT가 vision task에서 attention의 놀라운 힘을 보여주었다. 하지만 생성을 위한 잠재 변수 모델에 transformer를 사용하는 것은 여전히 한계가 있다. ViT는 패치 레벨에서 이미지를 처리하는 유연한 방법을 제공한다.
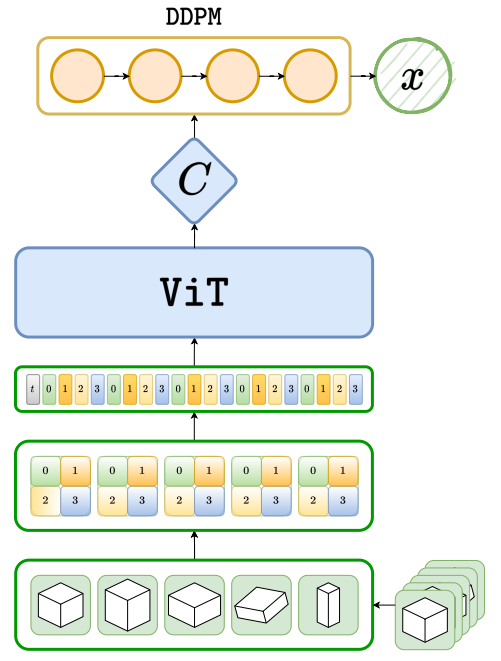
본 논문은 이미지들의 세트를 다루기 위한 ViT인 sViT를 사용한다. 기본적인 아이디어는 세트의 전역적인 정보를 추출하고 각 패치는 이미지의 특정 영역에 대한 전역적인 정보를 가지고 있어야 한다는 것이다. Layer embedding $t$에서의 ViT encoder를 $\textrm{ViT}(X, t; \phi)$로 컨디셔닝할 수 있다. 이를 통해 per layer에 의존하는 컨텍스트를 쉽게 학습할 수 있으며, 큰 $t$에서는 coarse한 컨텍스트를 학습하고 작은 $t$에서는 더 정제된 컨텍스트를 학습한다.
토큰을 입력으로 사용하면 일반적인 도메인에 구애받지 않는 few-shot generator를 사용할 수 있다. 본 논문의 접근 방식은 단순히 입력 세트를 토큰화하고 patch embedding layer를 finetuning하여 모든 양식(텍스트, 음성, 비전)으로 few-shot 및 조건부 생성에 쉽게 사용할 수 있다. Finetuning은 set encoder, 컨디셔닝 메커니즘, 생성 프로세스를 수정할 필요가 없다.
2. Conditioning the Generative Process
패치들로부터 $c$를 얻고나면 DDPM을 컨디셔닝하는 방법을 찾아야 한다. 저자들은 2가지 형태의 $c$로 컨디셔닝을 하였다. 하나는 벡터 $c \in \mathbb{R}^d$를 사용하는 방법이고 다른 하나는 $N$개의 토큰들의 컬렉션 $c \in \mathbb{R}^{N \times d}$을 사용하는 방법이다. 각각 FiLM과 Learnable Attentive Conditioning (LAC)을 사용하였다.
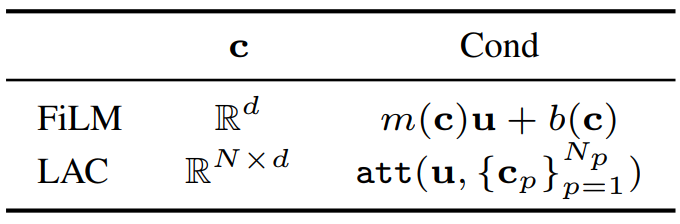
Vector (V)
접근법 중 하나는 FiLM과 같은 메커니즘으로 DDPM UNet의 중간 feature map $u$를 $c$로 컨디셔닝 하는 것이다. FiLM은
\[\begin{equation} u = m(c) u + b(c) \end{equation}\]로 표현할 수 있으며 $m$과 $b$는 학습 가능하고 컨텍스트에 의존한다. Diffusion model의 모든 layer들은 파라미터 $\theta$를 공유하며 step $t$의 embedding에 대해서만 다르다. 따라서 컨디셔닝 메커니즘은
\[\begin{equation} u = f(u, c, t) = f(u_t, c_t) \end{equation}\]로 쓸 수 있다. $c$를 step embedding과 병합하여 각 layer를 컨디셔닝할 수 있으며, 이는 일반적인 per-step 컨디셔닝 메커니즘이다. 실험을 통해 $u(c,t) = m(c)u(t) + b(c)$의 형태가 가장 성능이 좋고 유연함을 확인하였다고 한다.
Tokens (T)
$c$가 변수들의 컬렉션
\[\begin{equation} c = \{c_{sp}\}_{s=1,p=1}^{N_s, N_p} \end{equation}\]일 수 있다. 여기서 $N_p$는 샘플 당 패치의 개수이며 $N_s$는 세트의 샘플 수이다. 이 경우 attention을 사용하여 컨텍스트 $c$와 feature map $u$의 정보를 융합할 수 있다. 원칙적으로 패치를
\[\begin{equation} u = \textrm{attn} (u, \{c_{sp}\}_{s=1,p=1}^{N_s, N_p}) \end{equation}\]와 같이 직접 사용할 수 있다. 하지만 이 방법은 $N_s$에 따라 크게 확장되지 않는다. 다른 방법으로는 per-patch aggregation을 사용하여 세트 차원에서 평균하여 $N_p$개의 토큰 \(\{c_p\}_{p=1}^{N_p}\)를 얻고 ViT에 입력하는 것이다.
\[\begin{equation} c_p = \frac{1}{N_s} \sum_{s=1}^{N_s} c_{sp} \end{equation}\]그런 다음 패치당 평균 토큰
\[\begin{equation} u = \textrm{attn} (u, \{c_p\}_{p=1}^{N_p}) \end{equation}\]에서 cross-attention을 사용하여 DDPM을 컨디셔닝한다. Per-patch aggregation을 사용하면 토큰 수를 증가시키지 않고 어떤 샘플 수에 대해서도 DDPM을 컨디셔닝힐 수 있다. 또한 더 중요한 점은 $c$에서 서로 다른 샘플의 정보를 집계할 수 있다는 것이다.
3. Variational FSDM
FSDM 공식에 대한 대안으로 컨텍스트 $c$가 잠재 변수이고 세트 $X$가 $c$에 따라 생성되는 잠재 변수 모델을 지정할 수 있다. 이 모델을 Variational FSDM (VFSDM)이라 부르며 다음과 같이 쓸 수 있다.
\[\begin{equation} p_\theta (X_{0:T}, c) = p_\theta (c) \bigg[ \prod_{s=1}^S p_\theta (x_{0:T}^{(s)} \vert c) \bigg], \quad p_\theta (x_{0:T} \vert c) = p_\theta (x_T) \prod_{t=1}^T p_\theta (x_{t-1} \vert x_t, c) \end{equation}\]이 경우 inferece 모델은 parameter-free diffusion posterior와 $c$에 대하여 parameterize된 인코더의 결합이다.
\[\begin{equation} q_\phi (X_{1:T}, c \vert X_0) = \underbrace{q_\phi (c \vert X_0)}_{\textrm{Set Encoder}} \; \underbrace{\bigg[ \prod_{s=1}^S q (x_{1:T}^{(s)} \vert x_0^{(s)}, c) \bigg]}_{\textrm{Diffusion}}, \quad q (x_{1:T} \vert x_0, c) = \prod_{t=1}^T q (x_t \vert x_{t-1}, c) \end{equation}\]Negative ELBO는 인코더 $q_\phi (c \vert X_0)$와 prior $p(c)$ 사이의 추가 KL 항을 포함한다.
\[\begin{equation} L_\textrm{VFSDM} = \mathbb{E}_{q_\phi (c \vert X_0)} [L_\textrm{FSDM}] + \mathbb{KL} [q_\phi (c \vert x_0) \| p_\theta (c)] \end{equation}\]저자들은 원래 이 모델로 실험을 진행하였지만, 학습이 더 어려워서 성능이 저하되거나 컨디셔닝 속성이 좋지 않다는 것을 발견했다고 한다.
Experiments
- 데이터셋: Omniglot (28$\times$28), FS-CIFAR100 (32$\times$32), miniImageNet (32$\times$32), CelebA (64$\times$64)
- Setup
- Backbone: 표준 DDPM 모델 ($T = 1000$, linear $\beta$ schedule), 채널 수를 64로 줄임 (25M)
- 샘플 품질과 학습 안정성 사이의 균형을 위해 Improved DDPM의 $L = L_\epsilon + \lambda L_\textrm{vlb}$로 학습 ($\lambda = 0.001$)
- Set encoder: Unet (10M), ViT (5M)
1. Few-Shot Generation
다음은 여러 데이터셋과 여러 metric에 대한 few-shot 생성 평가 결과이다.
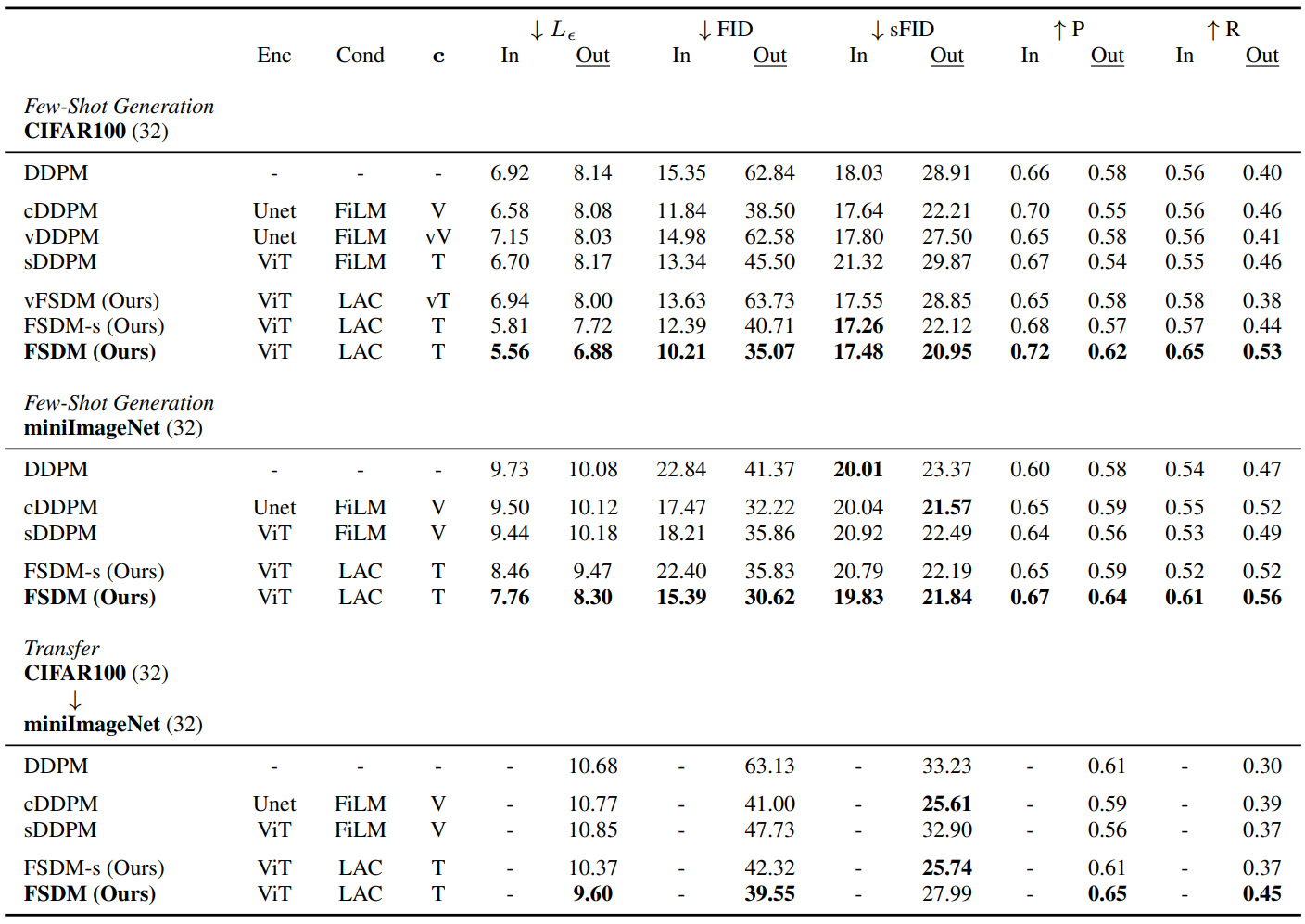
CIFAR100과 miniImageNet에서의 few-shot 생성과 CIFAR100에서 miniImageNet으로의 transfer를 테스트하였다. CIFAR100의 경우 오리지널 split을 사용했으며 모든 테스트 클래스는 새로운 카테고리이다.
“In”은 In-distribution, 즉 알고 있는 클래스들에 대하여 모델을 평가한 것이고, 반대로 “Out”은 Out-distribution, 즉 모르는 클래스들에 대하여 모델을 평가한 것이다 (few-shot task). $c$는 V (deterministic vector), T (deterministic tokens). vV (variational vector), vT (variationaltokens) 중 하나이다.
평가 지표는 $L_\epsilon$ (denoising loss), FID, sFID (spatial FID), P (precision), R (recall)을 사용하였다. 모델들을 학습하는 데 augmentation을 사용하지 않았다. 평가 지표 계산에는 1만 개의 샘플이 사용되었으며 250 step으로 생성되었다.
위 표에서 볼 수 있듯이 FSDM은 unconditional 및 conditional baseline과 비교했을 때 성능이 우수하였으며, cross-attention 컨디셔닝과 함께 사용하는 토큰 기반의 표현이 few-shot 생성을 위한 효과적인 메커니즘이라는 것을 보여준다.
다음은 CIFRA100에서 학습할 때의 layer당 $L_\epsilon$의 변화이다.
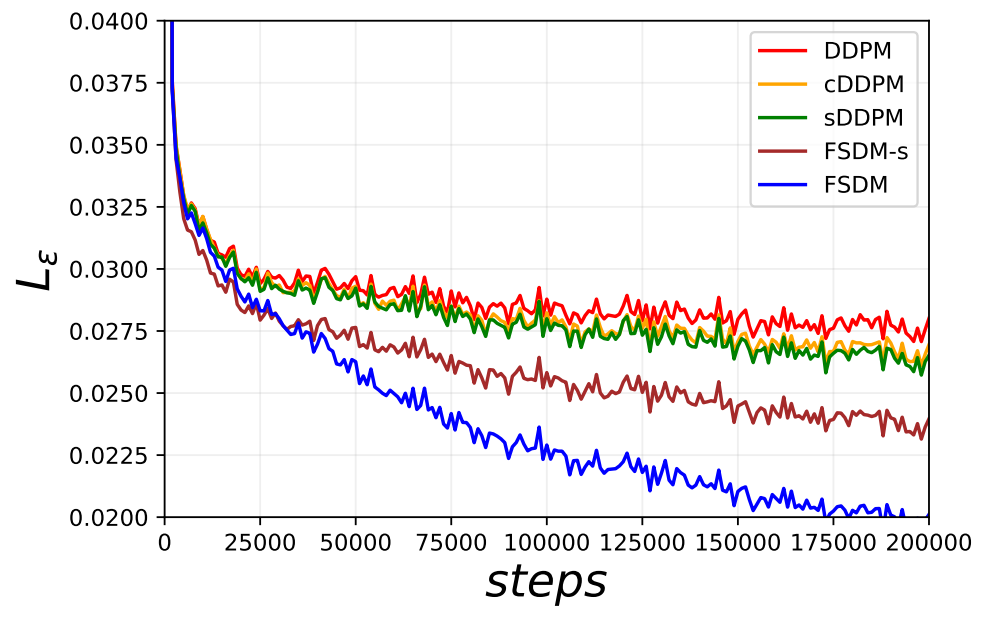
위 그래프에서 볼 수 있듯이 FSDM은 효율적으로 학습하며, 적은 데이터에서 더 많은 정보를 추출할 수 있고 더 빠르게 수렴한다.
2. Transfer
FSDM의 목표는 학습 중에 보지 못한 물체에 대한 few-shot 생성을 수행하는 것이다. 하지만 새로운 클래스들을 다룰 때 다양한 문제를 겪으며, 특히 새로운 클래스들이 새로운 카테고리나 새로운 데이터셋의 클래스인 경우 더 그렇다.
모델을 고양이와 사자에 대하여 학습한 후 호랑이를 테스트한다고 생각해보자. 인코더는 유사한 동물의 클래스를 활용하여 호랑이 세트에서 정보를 추출할 수 있다. 모델은 주어진 세트와 비슷한 클래스 사이를 “interpolate”할 수 있다.
하지만 만일 사과와 오렌지에 대하여 학습한 후 호랑이를 테스트한다고 하면 모델은 보다 근본적인 방식으로 문제를 겪게 된다. 알고 있는 클래스로 interpolate할 방법이 없으며 모델은 대부분 컨디셔닝 세트에 의존해야 한다.
이 두 경우 사이에는 few-shot 생성에서 겪는 문제의 정도가 다르다. 따라서 저자들은 모델이 얼마나 새로운 정보까지 적응할 수 있는지를 확인해 보았다. 이를 위해 다른 데이터셋에서 few-shot transfer을 테스트하였다. CIFAR100에서 학습한 모델을 miniImageNet에서 테스트하였다. 위 결과 표의 아래 부분에서 transfer 결과를 확인할 수 있다.
3. Sampling
다음은 FSDM을 이용하여 CIFAR100에서 few-shot으로 conditional하게 샘플링한 결과이다.

왼쪽은 in-distribution class의 컨디셔닝 세트와 샘플이다. 오른쪽은 out-distribution class의 컨디셔닝 세트와 샘플이다.
모르는 클래스의 시각적 품질은 알고 있는 클래스보다 분명히 나쁘다. 그러나 모델은 소수의 샘플과 복잡한 사실적 클래스에서 효과적인 방법으로 콘텐츠 정보를 추출할 수 있다.
4. Test-time conditioning
본 논문에서는 학습 중에 명시적으로 적응하는 것이 diffusion model을 조정하는 강력한 방법이라고 주장한다. 하지만 inferece에서 적응하는 것도 diffusion model을 새로운 분포에 적응시키는 효과적인 메커니즘인 것으로 나타났으며 모델이나 인코더를 재학습시킬 필요도 없다.
아래 표는 샘플링 시 사용하는 강력한 컨디셔닝 메커니즘인 ILVR을 학습 중에 모델을 컨디셔닝하는 FSDM과 비교한 결과이다.
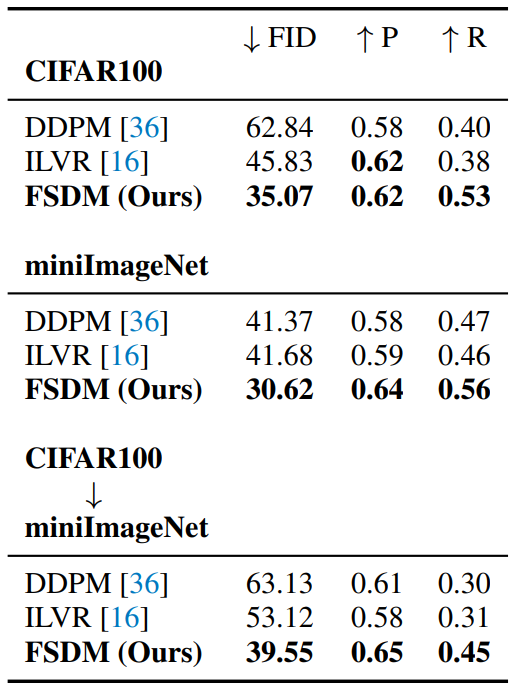
ILVR이 few-shot 생성에서 표준 unconditional DDPM 보다 개선된 결과를 보여준다. 하지만 필요한 적응이 새로운 속성이 아닌 새로운 클래스에 대한 것이다. FSDM은 ILVR보다 새로운 클래스에 대한 few-shot 성능이 좋았으며, 이는 학습 중에 컨디셔닝하는 것이 사실적이고 복잡한 물체에 대한 few-shot 생성에 꼭 필요하다는 증거이다.