[논문리뷰] FreeSplat: Generalizable 3D Gaussian Splatting Towards Free-View Synthesis of Indoor Scenes
NeurIPS 2024. [Paper] [Page] [Github]
Yunsong Wang, Tianxin Huang, Hanlin Chen, Gim Hee Lee
National University of Singapore
28 May 2024

Introduction
최근 3D Gaussian Splatting (3DGS)은 여러 시점에서 3D 장면을 사실적으로 재구성하기 위한 효율적인 표현으로 제안되었다. 3D Gaussian의 명시적 표현은 텍스처가 많은 영역에서 밀도가 높아지도록 최적화되며, rasterization 기반 볼륨 렌더링은 비용이 많이 드는 ray marching 방식을 피한다. 결과적으로 3DGS는 새로운 시점에서 고품질 이미지를 실시간으로 렌더링할 수 있었다. 그럼에도 불구하고 3DGS는 일반화가 부족하고 장면별 최적화가 필요하다.
3D Gaussian Splatting 일반화 능력을 제공하려는 시도가 여러 차례 있었다. 유망한 성능을 보여주었음에도 불구하고 이러한 방법은 장면 수준의 뷰 보간이나 물체 중심 합성에 국한된다. 주된 이유는 이러한 기존 방법이 Gaussian을 예측하기 위해 Transformer를 사용한 멀티뷰 이미지에서의 dense한 뷰 매칭에 의존하기 때문이다. 결과적으로 더 긴 시퀀스에서는 계산적으로 다루기 어려워지고 좁은 뷰 범위의 보간된 뷰들로 학습이 제한된다.
좁은 범위의 보간된 뷰들에 의한 학습은 종종 외삽(extrapolation)된 뷰에서 렌더링할 때 floater가 될 수 있는 localize가 잘못된 3D Gaussian을 생성한다. 또한 이 문제는 일반적으로 간단한 concatenation을 통해 멀티뷰 3D Gaussian을 병합하는 기존 방법으로 인해 더욱 악화되어 불가피하게 겹치는 영역에서 눈에 띄는 중복이 발생한다. 위에서 언급한 문제를 고려할 때, 임의의 포즈에서 실시간 렌더링을 지원할 수 있는 상당한 잠재력을 가진 글로벌한 3D Gaussian의 긴 시퀀스 재구성이 가능한 방법을 설계하는 것이 필수적이다.
본 논문에서는 실내 장면의 긴 시퀀스에 대한 자유 시점 합성에 맞춰진 FreeSplat을 제안하였다. 좁은 뷰 범위에서 뷰 보간에 국한된 기존 방법과 달리, FreeSplat은 넓은 뷰 범위에서 새로운 뷰 합성을 위해 글로벌한 Gaussian을 효과적으로 재구성할 수 있다. 전체 파이프라인은 Low-cost Cross-View Aggregation과 Pixel-wise Triplet Fusion (PTF)으로 구성된다.
Low-cost Cross-View Aggregation에서는 저비용 feature 추출 및 매칭을 위해 근처 뷰 간에 효율적인 CNN 기반 backbone과 적응적 cost volume을 도입한 다음, 멀티스케일 feature를 집계하여 cost volume의 receptive field를 넓히고 깊이와 Gaussian triplet을 예측한다.
그런 다음, PTF는 점진적 Gaussian 퓨전을 사용한 픽셀별 정렬을 통해 멀티뷰에서 local Gaussian triplet을 적응적으로 퓨전하고 겹치는 영역에서 Gaussian 중복성을 방지한다. 추가로, 효율적인 feature 추출 및 매칭을 통해 특정 개수의 뷰를 가진 일반화 가능한 3DGS를 풀어내고 긴 시퀀스에 대해 모델을 학습시키는 Free-View Training (FVT) 전략을 제안하였다.
Method
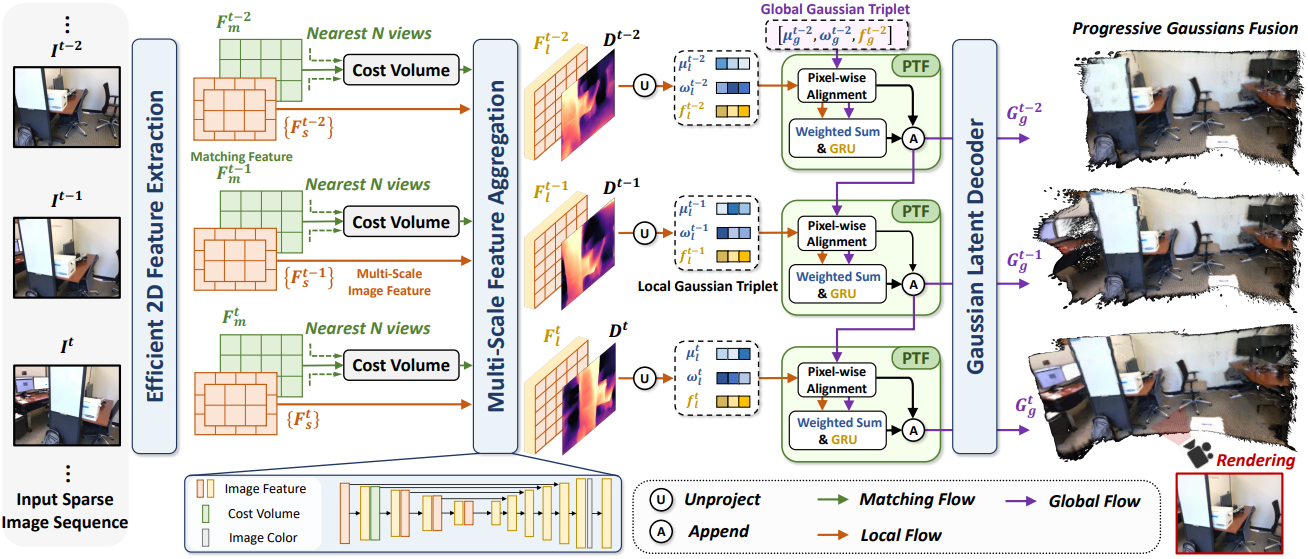
1. Overview
RGB 이미지 시퀀스가 주어지면, 근처 뷰 간에 cost volume을 적응적으로 구축하고, depth map을 예측하여 2D feature map을 3D Gaussian triplet으로 unprojection한다. 그런 다음 Pixel-wise Triplet Fusion (PTF) 모듈로 global Gaussian triplet을 local Gaussian triplet과 점진적으로 정렬하여 latent feature space에서 중복된 3D Gaussian을 융합하고 디코딩하기 전에 cross-view Gaussian feature를 집계할 수 있다. FreeSplat은 cost volume을 통해 cross-view feature를 효율적으로 교환하고, cross-view alignment와 adaptive fusion을 통해 뷰별 3D Gaussian을 점진적으로 집계할 수 있다.
2. Low-cost Cross-View Aggregation
효율적인 2D feature 추출
카메라 포즈를 아는 이미지 시퀀스 \(\{I^t\}_{t=1}^T\)가 주어지면, 먼저 이를 공유 2D backbone에 공급하여 멀티스케일 임베딩 $F_e^t$를 추출한다. Plane sweeping의 계산 비용을 줄이기 위해, 저차원 matching feature $F_m^t$을 임베딩하기 위한 ResNet을 학습시킨다. 계산 비용이 비싼 Transformer 기반 backbone에 의존하는 것과 달리, 저자들은 더 높은 해상도 입력에서 효율적인 성능을 위해 2D feature 추출에 순수 CNN 기반 backbone을 활용하였다.
Cost Volume
임의의 길이의 입력 이미지가 주어진 경우 카메라 포즈 정보를 명시적으로 통합하기 위해 근처 뷰 간에 cost volume을 적응적으로 구축한다. 포즈가 $P^t$고 matching feature가 $F_m^t \in \mathbb{R}^{C_m \times \frac{H}{4} \times \frac{W}{4}}$인 현재 뷰 $I^t$에 대해 포즈 근접성을 기반으로 포즈 \(\{P^{t_n}\}_{n=1}^N\)을 갖는 $N$개의 근처 뷰 \(\{I^{t_n}\}_{n=1}^N\)을 적응적으로 선택하고 plane sweep stereo를 통해 cost volume을 구성한다.
구체적으로, 내부에 균일한 간격으로 $K$개의 가상 깊이 평면 \(\{d_k\}_{k=1}^K\)를 정의하고 근처 뷰 feature를 현재 뷰의 각 깊이 평면 $d_k$로 워핑한다.
\[\begin{equation} \tilde{F}_m^{t_n, k} = \textrm{Trans} (P^{t_n}, P^t) F_m^{t_n} \end{equation}\]\(\textrm{Trans} (P^{t_n}, P^t)\)는 뷰 $t_n$에서 $t$로의 transformation matrix이다. Cost volume \(F_\textrm{cv}^t$ \in \mathbb{R}^{K \times \frac{H}{4} \times \frac{W}{4}}\)는 다음과 같이 정의된다.
\[\begin{equation} F_\textrm{cv}^t [k] = f_\theta \bigg( (\frac{1}{N} \sum_{n=1}^N \cos (F_m^t, \tilde{F}_m^{t_n, k})) \oplus (\frac{1}{N} \sum_{n=1}^N \tilde{F}_m^{t_n, k}) \bigg) \end{equation}\](\(F_\textrm{cv}^t [k]\)는 \(F_\textrm{cv}^t\)의 $k$번째 차원, $f_\theta$는 1$\times$1 CNN, $\cos$는 cosine similarity, $\oplus$는 feature-wise concatenation)
멀티스케일 feature 집계
Cost volume의 임베딩은 3D Gaussian을 정확하게 localize하는 데 중요한 역할을 한다. 이를 위해 멀티스케일 인코더-디코더 구조를 설계하여 멀티스케일 이미지 feature를 cost volume과 융합하고 cost volume 정보를 더 넓은 receptive field로 전파한다.
구체적으로, 멀티스케일 인코더는 \(F_\textrm{cv}^t\)를 입력하고 출력은 {F t s }와 연결된 다음 UNet++ 유사 디코더로 보내 전체 해상도로 업샘플링하고 depth candidates map $D_c^t \in \mathbb{R}^{K \times H \times W}$와 Gaussian triplet map $F_l^t \in \mathbb{R}^{C \times H \times W}$를 예측한다. 그런 다음 soft-argmax을 통해 depth map을 예측한다.
\[\begin{equation} D^t = \sum_{k=1}^K \textrm{softmax} (D_c^t)_k \cdot d_k \end{equation}\]마지막으로, Gaussian triplet map \(F_l^t\)은 3D Gaussian triplet \(\{\mu_l^t, \omega_l^t, f_l^t\}\)로 unprojection된다. 여기서 \(\mu_l^t \in \mathbb{R}^{3 \times HW}\)는 Gaussian 중심이고, \(\omega_l^t \in \mathbb{R}^{1 \times HW}\)는 $(0, 1)$ 사이의 가중치이며, \(f_l^t \in \mathbb{R}^{(C-1) \times HW}\)는 Gaussian triplet feature이다.
3. Pixel-wise Triplet Fusion
이전 generalizable 3DGS 방법의 한 가지 한계는 Gaussian의 중복성이다. 실내 장면에서 정확하게 localize된 3D Gaussian을 예측하려면 멀티뷰 관찰이 필요하기 때문에 픽셀 정렬된 Gaussian은 자주 관찰되는 영역에서 중복된다. 더욱이 이전 방법은 불투명도를 통해 동일한 영역의 멀티뷰 Gaussian을 통합하여 사후 집계가 부족하여 최적이 아닌 성능을 초래한다.
저자들은 겹치는 영역에서 중복 Gaussian을 상당히 제거하고 latent space에서 멀티뷰 feature를 명시적으로 집계할 수 있는 Pixel-wise Triplet Fusion (PTF) 모듈을 제안하였다. Pixel-wise Alignment를 사용하여 뷰별 local Gaussian을 global Gaussian과 정렬하여 중복 3D Gaussian Triplet을 선택하고 local Gaussian을 점진적으로 global Gaussian으로 융합한다.
Pixel-wise Alignment
Gaussian triplet \(\{\mu_l^t, \omega_l^t, f_l^t\}_{t=1}^T\)이 주어지면, global Gaussian latent가 비어 있는 $t = 1$에서 시작한다. $t$번째 step에서, 먼저 global Gaussian triplet의 중심 \(\mu_g^{t-1} \in \mathbb{R}^{3 \times M}\)을 $t$번째 뷰에 project한다.
\[\begin{equation} p_g^t := \{ x_g^t, y_g^t, d_g^t \} = P^t \mu_g^{t-1} \in \mathbb{R}^{3 \times M} \end{equation}\]그런 다음 local Gaussian triplet을 threshold 내의 픽셀별로 가장 가까운 projection과 대응시킨다. 구체적으로, $i$번째 local Gaussian의 2D 좌표 $[x_l^t (i), y_l^t (l)]$와 깊이 $d_l^t (j)$의 경우, 먼저 픽셀 내 global projection set \(\mathcal{S}_i\)를 찾는다. ($[\cdot]$은 반올림)
\[\begin{equation} \mathcal{S}_i^t = \{j \; \vert \; [x_g^t (j)] = x_l^t (i), \, [y_g^t (j)] = y_l^t (i)\} \end{equation}\]그 후, threshold 내에서 깊이 차이가 최소인 유효한 correspondence를 검색한다.
\[\begin{equation} m_i = \begin{cases} \underset{j \in \mathcal{S}_i^t}{\arg \min} \; d_g^t (j) & \quad \textrm{if} \; \vert d_l^t (j) - \min_{j \in \mathcal{S}_i^t} d_g^t (j) \vert < \delta \cdot d_l^t (j) \\ \varnothing & \quad \textrm{otherwise} \end{cases} \end{equation}\]유효한 correspondence의 집합을 다음과 같이 정의한다.
\[\begin{equation} \mathcal{F}^t := \{ (i, m_i) \; \vert \; i = 1, \ldots, HW; \, m_i \ne \varnothing \} \end{equation}\]Gaussian Triplet Fusion
Pixel-wise Alignment 후, 유효하게 정렬된 triplet 쌍을 병합하여 중복된 3D Gaussian을 제거한다. Triplet 쌍 $(i, m_i) \in \mathcal{F}^t$가 주어지면, 3D Gaussian 중심이 triplet 쌍 사이에 있도록 제한하기 위해, 중심 좌표를 가중 합산하고 가중치를 합산한다.
\[\begin{equation} \mu_g^t (m_i) = \frac{\omega_l^t (i) \mu_l^t (i) + \omega_g^{t-1} (m_i) \mu_g^{t-1} (m_i)}{\omega_l^t (i) + \omega_g^t (m_i)} \\ \omega_g^t (m_i) = \omega_l^t (i) + \omega_g^{t-1} (m_i) \end{equation}\]Local Gaussian latent feature와 global Gaussian latent feature를 집계하기 위해 가벼운 GRU 네트워크를 통해 global Gaussian latent feature를 업데이트한다.
\[\begin{equation} f_g^t (m_i) = \textrm{GRU} (f_l^t (i), f_g^{t-1} (m_i)) \end{equation}\]그런 다음 다른 local Gaussian triplet은 global Gaussian triplet에 추가된다.
Gaussian primitives decoding
PTF 후에 global Gaussian triplet을 Gaussian으로 디코딩할 수 있다.
\[\begin{equation} \mu = \mu_g^T, \quad \Sigma, \alpha, s = \textrm{MLP}_d (f_g^T) \end{equation}\]제안된 융합 방식은 기하학적 제약 조건과 학습 가능한 GRU 네트워크를 사용해 Gaussian을 점진적으로 통합해 feature를 업데이트할 수 있으며, 이를 통해 중복된 Gaussian을 상당히 제거하고 여러 시점에서 feature 집계를 수행할 수 있으며, 적절한 계산 오버헤드로 다른 프레임워크 구성 요소와 함께 end-to-end 학습이 가능하다.
4. Training
Loss Functions
3D Gaussian을 예측한 후 새로운 뷰에서 렌더링한다. MVSplat이나 pixelSplat과 유사하게, MSE loss와 LPIPS loss을 사용하며, 가중치는 각각 1과 0.05이다.
Free-View Training
저자들은 3D Gaussian의 localization에 더 많은 기하학적 제약을 추가하고 특정 수의 입력 뷰를 가진 generalizable 3DGS의 성능을 풀어내기 위해 Free-View Training (FVT) 전략을 제안하였다. 이를 위해 무작위로 $T$개의 컨텍스트 뷰를 샘플링하고 (2 ~ 8) 더 넓은 뷰 보간에서 학습시킨다. 긴 시퀀스 학습은 효율적인 feature 추출 및 집계로 인해 실현 가능하다. FVT는 새로운 뷰에서 깊이 추정에 상당히 기여한다.
Experiments
- 데이터셋: ScanNet, Replica
- 구현 디테일
- optimizer: Adam
- learning rate: $1 \times 10^{-4}$
- iteration: 30만
- batch size: 1
- 이미지 해상도: 512$\times$384
1. Results on ScanNet
다음은 ScanNet에서의 뷰 보간 결과이다.
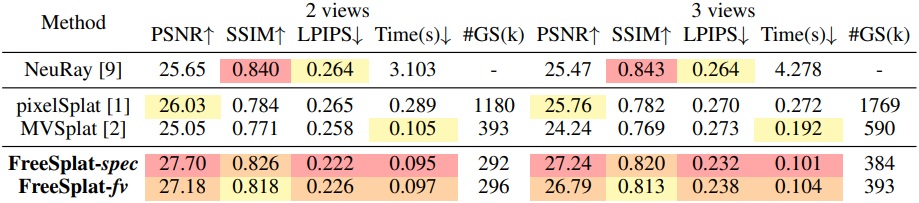
다음은 긴 시퀀스에서의 재구성 결과이다.


다음은 ScanNet에서의 깊이 렌더링 결과이다.
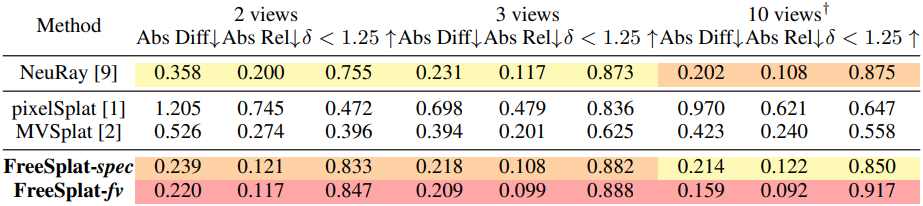
2. Zero-Shot Transfer Results on Replica
다음은 Replica에서의 zero-shot transfer 결과이다.

3. Ablation Study
다음은 ScanNet에서의 ablation 결과이다.

