[논문리뷰] FreGS: 3D Gaussian Splatting with Progressive Frequency Regularization
CVPR 2024. [Paper]
Jiahui Zhang, Fangneng Zhan, Muyu Xu, Shijian Lu, Eric Xing
Nanyang Technological University | Max Planck Institute for Informatics | Carnegie Mellon University | MBZUAI
11 Mar 2024

Introduction
NeRF의 강력한 대안인 3D Gaussian splatting (3D-GS)은 경쟁력 있는 렌더링 품질을 유지하면서 뛰어난 학습 및 inference 속도를 제공함으로써 점점 더 많은 주목을 받고 있다. Gaussian 속성의 적응형 밀도 제어와 함께 3D Gaussian을 도입함으로써 3D-GS는 novel view synthesis (NVS)를 위한 탁월하고 명확한 장면 표현을 학습할 수 있다. NeRF의 번거로운 볼륨 렌더링을 효율적인 스플래팅으로 대체하여 3D Gaussian을 2D 평면에 직접 projection하고 실시간 렌더링을 보장한다. 그러나 3D-GS는 종종 Gaussian densification 중에 over-reconstruction으로 인해 어려움을 겪는다. 여기서 고분산 이미지 영역은 몇 개의 큰 Gaussian으로만 덮혀 학습된 표현에 명확한 결함이 발생한다. Over-reconstruction은 렌더링된 2D 이미지의 blur 및 아티팩트뿐만 아니라 렌더링된 이미지와 ground-truth의 주파수 스펙트럼 불일치를 통해 명확하게 관찰된다.
본 논문은 over-reconstruction이 주파수 스펙트럼의 불일치로 인해 명확하게 나타난다는 관찰을 바탕으로 푸리에 공간에서 주파수 신호를 정규화하여 over-reconstruction을 해결하는 3D-GS 기술인 FreGS를 설계했다. FreGS는 점진적인 주파수 정규화를 위해 새로운 주파수 어닐링 기술을 도입하였다. 특히 저주파 신호와 고주파 신호가 각각 전체 패턴 및 구조와 로컬 디테일을 인코딩한다는 근거를 기반으로 저주파 신호에서 고주파 신호로 정규화를 점진적으로 어닐링하여 coarse-to-fine Gaussian densification을 수행한다. 점진적인 정규화는 렌더링된 이미지와 ground-truth의 주파수 스펙트럼 불일치를 최소화하기 위해 노력하며, 이는 주파수 공간에서 충실한 guidance를 제공하고 픽셀 레벨 L1 loss를 효과적으로 보완한다. FreGS는 over-reconstruction을 완화하고 Gaussian densification과 novel view synthesis를 크게 향상시킨다.
Method

위 그림은 FreGS의 개요이다. 저자들은 먼저 over-reconstruction 문제를 해결하고 Gaussian densification을 개선하는 데 있어 주파수 정규화가 효과적인 이유를 밝혔다. 그런 다음 푸리에 공간 내에서 주파수 정규화에 사용되는 진폭 및 위상 불일치를 설명하였다. 이를 바탕으로 Gaussian densification의 어려움을 줄이기 위해 점진적인 주파수 정규화를 위한 주파수 어닐링 기술을 설계하였다. 이는 주파수 성분으로 점진적으로 활용하여 coarse-to-fine Gaussian densification을 수행할 수 있다.
1. Frequency Regularization
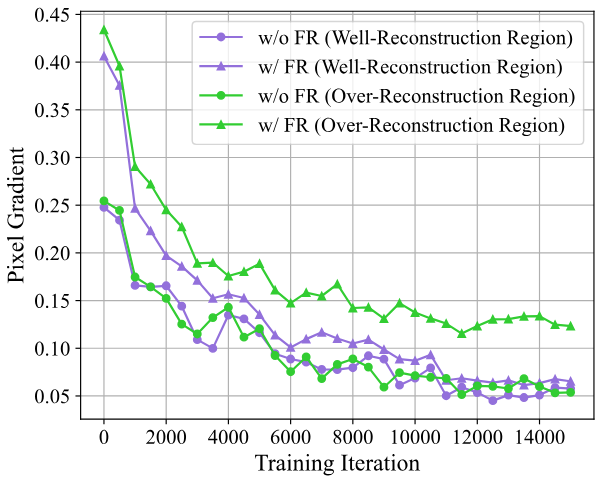
먼저 3D-GS가 over-reconstruction으로 이어지는 이유를 살펴보자. 저자들은 학습이 진행됨에 따라 변화를 추적하면서 over-reconstruction 영역 내 픽셀의 평균 기울기를 계산하였다. 위 그림에서 볼 수 있듯이 naive한 픽셀별 L1 loss를 사용하면 영역이 잘 재구성되지 않더라도 평균 기울기가 매우 작을 수 있으며 이는 Gaussian densification을 잘못 유도한다. 특히 작은 픽셀 기울기는 이 픽셀과 해당 3D Gaussian에 대한 2D splat으로 역전파된다. 작은 기울기를 갖는 Gaussian에는 Gaussian densification이 적용되지 않으므로 이러한 Gaussian은 더 작은 Gaussian으로 분할하여 densify할 수 없으므로 over-reconstruction이 발생한다.
Over-reconstruction의 결과로 영역 표현이 불충분해져 전체 구조(저주파 정보)와 디테일(고주파 정보) 모두에서 결함이 발생한다. 픽셀 공간과 비교하여 over-reconstruction 영역은 서로 다른 주파수 성분을 명시적으로 분리하여 주파수 공간에서 더 잘 드러날 수 있다. 따라서 주파수 도메인에서 densification을 명시적으로 적용하여 Gaussian densification을 가이드하는 것이 직관적이다. 위 그림은 주파수 정규화에 따라 평균 픽셀 기울기가 크게 증가하여 효율성을 입증한다. 따라서 저자들은 주파수 정규화를 통해 over-reconstruction 영역에서 Gaussian이 적응적으로 densify될 수 있다는 결론을 내렸다. 대조적으로, L1 loss는 over-reconstruction된 영역과 잘 재구성된 영역을 구별할 수 없으므로 잘 재구성된 영역에 중복된 Gaussian이 많이 생성된다.
위의 분석을 바탕으로 저자들은 주파수 관점에서 3D-GS를 향상시키는 것을 목표로 하는 FreGS를 설계하였다. 특히, 렌더링된 이미지와 ground-truth의 주파수 스펙트럼 사이의 불일치를 최소화하여 over-reconstruction을 완화하고 Gaussian densification을 향상시킨다. 주파수의 두 가지 주요 요소인 진폭과 위상은 이미지의 다양한 정보를 캡처할 수 있다. 따라서 푸리에 공간 내에서 렌더링된 이미지 $\hat{I} \in \mathbb{R}^{H \times W \times C}$와 ground-truth $I \in \mathbb{R}^{H \times W \times C}$ 사이의 진폭 및 위상 불일치를 정규화하여 주파수를 정규화한다.
먼저 2D 이산 푸리에 변환을 통해 $\hat{I}$와 $I$를 각각의 주파수 표현 $\hat{F}$와 $F$로 변환한다. $I$를 예로 들면 다음과 같다.
\[\begin{equation} F(u, v) = \sum_{x=0}^{H-1} \sum_{y=0}^{W-1} I (x,y) \cdot \exp (-i 2 \pi (u \frac{x}{H} + v \frac{y}{W})) \end{equation}\]여기서 $(x, y)$와 $(u, v)$는 각각 이미지와 주파수 스펙트럼의 좌표이다. 그러면 각 푸리에 표현은 진폭과 $\vert F(u, v) \vert$와 위상 $\angle F(u, v)$로 표현될 수 있다.
\[\begin{aligned} \vert F (u, v) \vert &= \sqrt{\textrm{Re} (u, v)^2 + \textrm{Im} (u, v)^2} \\ \angle F (u, v) &= \textrm{arctan} (\frac{\textrm{Im} (u, v)}{\textrm{Re} (u, v)}) \end{aligned}\]여기서 $$\textrm{Re}(u, v)$와 $\textrm{Im}(u, v)$는 $F(u, v)$의 실수 부분과 허수 부분이다.
$\hat{I}$와 $I$ 사이의 진폭 및 위상 불일치 $d_a$와 $d_p$는 유클리드 메트릭을 사용하여 얻을 수 있다. 또한, 모든 주파수 성분의 진폭과 위상을 계산하여 차이를 정확하게 평가한 후 이를 평균하여 다음과 같이 최종 불일치를 도출한다.
\[\begin{aligned} d_a &= \frac{1}{\sqrt{HW}} \sum_{x=0}^{H-1} \sum_{y=0}^{W-1} \bigg\vert \vert F (u, v) \vert - \vert \hat{F} (u, v) \vert \bigg\vert \\ d_p &= \frac{1}{\sqrt{HW}} \sum_{x=0}^{H-1} \sum_{y=0}^{W-1} \bigg\vert \angle F (u, v) - \angle \hat{F} (u, v) \bigg\vert \end{aligned}\]3. Frequency Annealing

위 그림에서 볼 수 있듯이, 진폭 및 위상 불일치를 naive하게 채택하면 주파수 정규화가 낮은 주파수와 높은 주파수를 구분하지 않고 over-reconstruction을 어느 정도 완화할 수 있기는 하지만 여전히 제한된 Gaussian densification 문제를 겪고 있으며 3D-GS를 바람직하지 않은 아티팩트 쪽으로 크게 편향시킨다. 저주파와 고주파는 각각 대규모 feature(ex. 글로벌 패턴 및 구조)와 소규모 feature(ex. 로컬 디테일)과 관련되므로 저자들은 점진적인 주파수 정규화를 수행하는 주파수 어닐링 기술을 설계하여 coarse-to-fine Gaussian densification을 수행하였다. 주파수 어닐링 기술을 사용하면 위 그림과 같이 우수한 Gaussian densification을 달성될 수 있다.
구체적으로, low-pass filter $H_l$과 dynamic high-pass filter $H_h$를 푸리에 공간에 통합하여 각각 저주파 $\textrm{LF} (u, v)$와 고주파 $\textrm{HF} (u, v)$를 추출한다.
\[\begin{aligned} \textrm{LF} (u,v) &= F(u, v) H_l (u, v) \\ \textrm{HF} (u,v) &= F(u, v) H_h (u, v) \end{aligned}\]저주파와 고주파에 해당하는 진폭과 위상 불일치는 다음과 같다. (l은 저주파, h는 고주파, a는 진폭, p는 위상)
\[\begin{aligned} d_{la} &= \frac{1}{\sqrt{HW}} \sum_{x=0}^{H-1} \sum_{y=0}^{W-1} \bigg\vert \vert \textrm{LF} (u, v) \vert - \vert \hat{\textrm{LF}} (u, v) \vert \bigg\vert \\ d_{lp} &= \frac{1}{\sqrt{HW}} \sum_{x=0}^{H-1} \sum_{y=0}^{W-1} \bigg\vert \angle \textrm{LF} (u, v) - \angle \hat{\textrm{LF}} (u, v) \bigg\vert \\ d_{ha} &= \frac{1}{\sqrt{HW}} \sum_{x=0}^{H-1} \sum_{y=0}^{W-1} \bigg\vert \vert \textrm{HF} (u, v) \vert - \vert \hat{\textrm{HF}} (u, v) \vert \bigg\vert \\ d_{hp} &= \frac{1}{\sqrt{HW}} \sum_{x=0}^{H-1} \sum_{y=0}^{W-1} \bigg\vert \angle \textrm{HF} (u, v) - \angle \hat{\textrm{HF}} (u, v) \bigg\vert \end{aligned}\]먼저 저주파 불일치를 정규화하기 시작한 다음 학습이 진행됨에 따라 점차적으로 고주파 성분을 통합한다. 고주파의 점진적 통합은 dynamic high-pass filter $H_h$를 사용하여 달성할 수 있으며, 여기서 $t$번째 iteration에서 통과할 수 있는 주파수 대역 범위 $D_t$는 다음과 같이 표현될 수 있다.
\[\begin{equation} D_0 < D_t < \frac{(t - T_0) (D - D_0)}{T - T_0} + D_0 \end{equation}\]여기서 $D_0$와 $D$는 각각 low-pass filter가 허용하는 최대 범위와 주파수 스펙트럼의 최대 범위이다. 중심점 $(H/2, W/2)$을 좌표 원점으로 사용한다. $t$는 현재 iteration, $T_0$는 고주파 성분 사용 시작 iteration, $T$는 고주파 성분 사용 종료 iteration이다. 낮은 주파수에서 높은 주파수까지 정규화를 적용하면 coarse-to-fine Gaussian densification을 얻을 수 있다. 점진적 주파수 정규화 \(\mathcal{L}_f\)는 다음과 같다.
\[\begin{equation} \mathcal{L}_f = \begin{cases} w_l (d_{la} + d_{lp}) & \quad 0 < t \le T_0 \\ w_l (d_{la} + d_{lp}) + w_h (d_{ha} + d_{hp}) & \quad t > T_0 \end{cases} \end{equation}\]여기서 $w_l$과 $w_h$는 각각 저주파와 고주파에 대한 학습 가중치이다.
Experiments
- 데이터셋: Mip-NeRF360, Tanks&Temples, Deep Blending
- 구현 디테일
- Gaussian densification이 끝나면 주파수 정규화가 종료
- 안정적인 최적화를 위해 원본보다 4배 작은 이미지 해상도로 최적화를 시작
- 500 iteration 이후 이미지 해상도를 원본 해상도로 증가시킴
- optimizer: Adam
1. Comparisons with the State-of-the-Art


2. Ablation Studies
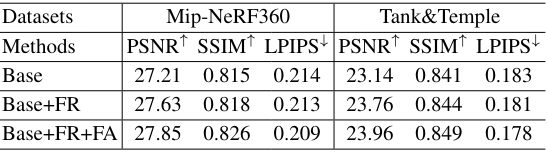
다음은 주파수 정규화 (FR)와 주파수 어닐링 (FA)에 대한 ablation 결과이다.
3. Visualizations
다음은 학습 프로세스에 따른 Gaussian densification과 렌더링된 이미지를 시각화한 것이다.

FreGS는 더 많은 Gaussian을 생성하고 over-reconstruction된 영역에 대하여 더 나은 Gaussian densification을 얻는다. 15,000 iteration 이후에는 Gaussian densification이 종료되어 Gaussian 수가 더 이상 변하지 않는다.