[논문리뷰] Focal Modulation Network (FocalNet)
NeurIPS 2022. [Paper] [Page]
Jianwei Yang, Chunyuan Li, Xiyang Dai, Lu Yuan, Jianfeng Gao
Microsoft Research | Microsoft Cloud + AI
22 Mar 2022

Introduction
원래 자연어 처리 (NLP)용으로 제안된 Transformer는 ViT 이후 컴퓨터 비전에서 널리 사용되는 아키텍처가 되었다. 이미지 분류, object detection, segmentation 등 다양한 비전 task에서 그 가능성이 입증되었다. Transformer에서 self-attention (SA)은 공유 커널이 있는 로컬 영역의 상호 작용을 제한하는 convolution 연산과 달리 입력에 의존하는 글로벌 상호 작용을 가능하게 하는 성공의 핵심이다. 이러한 장점에도 불구하고 SA의 효율성은 특히 고해상도 입력의 경우 시각적 토큰 수에 대한 2차 복잡도로 인해 우려되었다. 이를 해결하기 위해 많은 연구에서 token coarsening, window attention, dynamic token selection 또는 하이브리드를 통해 SA 변형들을 제안했다. 한편, 로컬 구조를 잘 인식하면서 장거리 의존성을 포착하기 위해 SA를 (depth-wise) convolution으로 강화하여 여러 모델이 제안되었다.

본 논문에서는 입력에 의존하는 장거리 상호 작용을 모델링하는 데 SA보다 더 좋은 방법이 있는가라는 근본적인 질문에 답하는 것을 목표로 한다. SA의 현재 고급 디자인에 대한 분석부터 시작한다. 위 그림의 왼쪽에서는 ViT와 Swin Transformer에서 제안된 빨간색 query 토큰과 주변 주황색 토큰 사이에 일반적으로 사용되는 (window-wise) attention을 보여준다. 출력을 생성하기 위해 SA에는 무거운 query-key 상호 작용 (빨간색 화살표)과 query와 다수의 공간적으로 분산된 토큰 (context feature) 간의 무거운 query-value 집계 (노란색 화살표)가 포함된다.
그런데 이렇게 무거운 상호작용과 집계를 수행할 필요가 있을까? 본 논문에서는 먼저 각 query를 중심으로 컨텍스트를 집계한 다음 집계된 컨텍스트로 쿼리를 적응적으로 변조하는 대체 방법을 사용한다. 위 그림의 오른쪽에 표시된 것처럼 query에 구애받지 않는 focal aggregation (ex. depth-wise convolution)을 간단히 적용하여 다양한 세분성 레벨에서 요약된 토큰을 생성할 수 있다. 그 후, 요약된 토큰은 modulator로 적응적으로 집계되어 최종적으로 query에 주된다.
이러한 변경은 여전히 입력에 의존하는 토큰 상호 작용을 가능하게 하지만 개별 query에서 집계를 분리하여 프로세스를 크게 단순화하여 단지 몇 가지 feature들만으로 상호 작용을 가볍게 만든다. 본 논문의 방법은 세밀하고 대략적인 시각적 컨텍스트를 포착하기 위해 여러 레벨의 집계를 수행하는 focal attention에서 영감을 받았다. 그러나 본 논문의 방법은 각 query 위치에서 modulator를 추출하고 query-modulator 상호 작용을 위해 훨씬 간단한 방법을 활용한다. 이 새로운 메커니즘을 Focal Modulation이라고 부르며, 이를 통해 SA를 대체하여 attention 없는 아키텍처인 Focal Modulation Network 또는 줄여서 FocalNet을 구축한다.
Focal Modulation Network
1. From Self-Attention to Focal Modulation
입력으로 시각적 feature map $X \in \mathbb{R}^{H \times W \times C}$가 주어지면 일반 인코딩 프로세스는 주변 $X$와의 상호 작용 $\mathcal{T}$와 컨텍스트에 대한 집계 $\mathcal{M}$을 통해 각 시각적 토큰 (query) $x_i \in \mathbb{R}^C$에 대한 feature 표현 $y_i \in \mathbb{R}^C$를 생성한다.
Self-attention
Self-attention 모듈은 다음과 같이 공식화된 늦은 집계 절차를 사용한다.
\[\begin{equation} y_i = \mathcal{M}_1 (\mathcal{T}_1 (x_i, X), X) \end{equation}\]여기서 컨텍스트 $X$에 대한 집계 \(\mathcal{M}_1\)은 query와 타겟 간의 attention 점수가 상호 작용 \(\mathcal{T}_1\)을 통해 계산된 후에 수행된다.
Focal modulation
대조적으로, focal modulation은 다음과 같이 공식화된 이른 집계 절차를 사용하여 정제된 표현 $y_i$를 생성한다.
\[\begin{equation} y_i = \mathcal{T}_2 (\mathcal{M}_2 (i, X), x_i) \end{equation}\]여기서 컨텍스트 feature는 먼저 각 위치 $i$에서 \(\mathcal{M}_2\)를 사용하여 집계된 다음 query는 \(\mathcal{T}_2\)를 기반으로 집계된 feature와 상호 작용하여 $y_i$를 형성한다.
위 두 식을 비교하면 다음을 확인할 수 있다.
- Focal modulation의 컨텍스트 집계 \(\mathcal{M}_2\)는 공유 연산자 (ex. depth-wise convolution)를 통해 컨텍스트 계산을 분할하는 반면, SA의 \(\mathcal{M}_1\)은 다양한 query에 대해 공유할 수 없는 attention 점수를 합산해야 하기 때문에 계산 비용이 더 많이 든다.
- 상호 작용 \(\mathcal{T}_2\)는 토큰과 해당 컨텍스트 간의 간단한 연산자인 반면, \(\mathcal{T}_1\)은 2차 복잡도를 갖는 토큰 간 attention 점수 계산을 포함한다.
Focal modulation 식을 기반으로 다음과 같이 focal modulation을 인스턴스화한다.
\[\begin{equation} y_i = q(x_i) \odot m (i, X) \end{equation}\]여기서 $q(\cdot)$는 query projection 함수이며 $\odot$는 element-wise 곱셈이다. $m(\cdot)$은 출력이 modulator라고 불리는 컨텍스트 집계 함수이다.
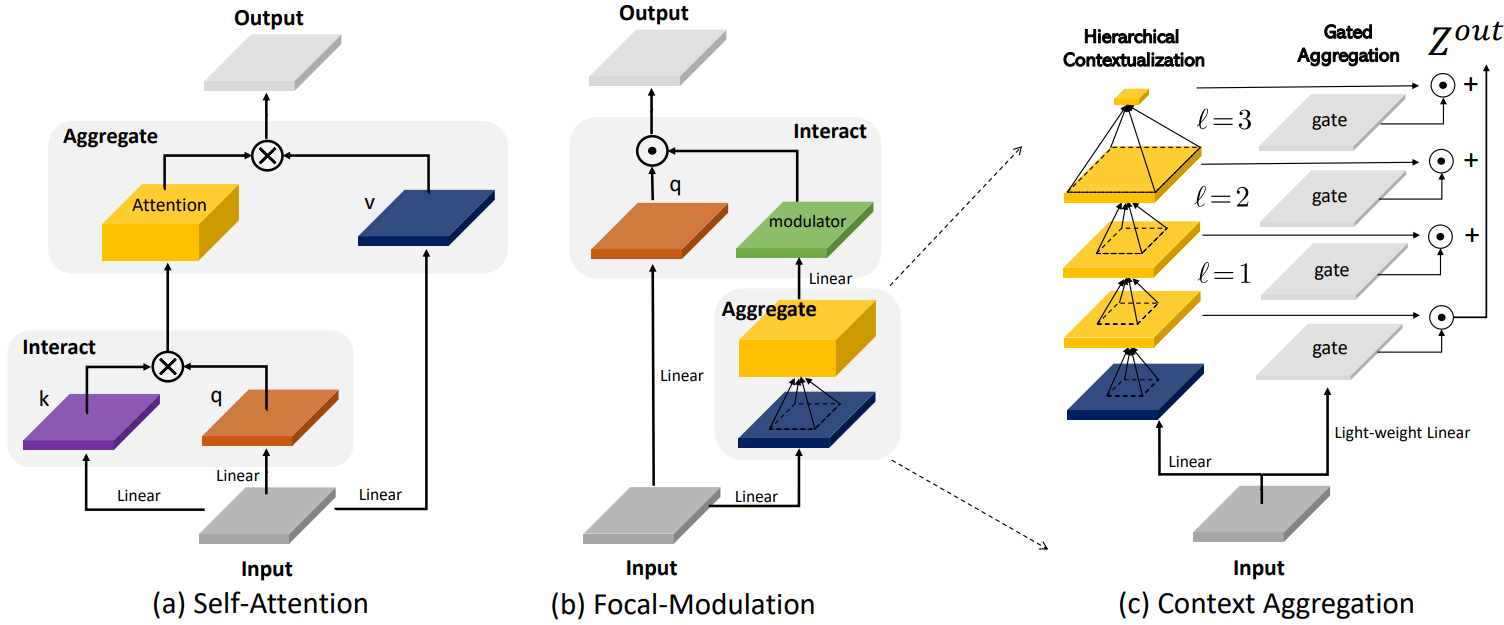
위 그림의 (a)와 (b)는 Self-Attention과 Focal Modulation을 비교한다. 제안된 focal modulation은 다음과 같은 유리한 특성을 갖는다.
- Translation invariance: $q(\cdot)$와 $m(\cdot)$은 항상 query 토큰 $i$의 중심에 있고 위치 임베딩이 사용되지 않으므로 modulation은 입력 feature map $X$의 평행 이동에 변하지 않는다.
- Explicit input-dependency: modulator는 타겟 위치 $i$ 주변의 로컬 feature를 집계하여 $m(\cdot)$을 통해 계산되므로 focal modulation은 명시적으로 입력에 의존한다.
- Spatial- and channel-specific: $m(\cdot)$에 대한 포인터인 타겟 위치 $i$는 공간별 modulation을 가능하게 한다. Element-wise 곱셈을 통해 채널별 modulation이 가능해진다.
- Decoupled feature granularity: $q(\cdot)$는 개별 토큰에 대한 가장 정밀한 정보를 보존하는 반면, $m(\cdot)$은 더 대략적인 컨텍스트를 추출한다. 이들은 분리되어 있지만 modulation을 통해 결합된다.
2. Context Aggregation via $m(\cdot)$
단거리 및 장거리 컨텍스트가 모두 시각적 모델링에 중요하다는 것이 입증되었다. 그러나 더 큰 receptive field를 가진 하나의 집계는 시간과 메모리 측면에서 계산 비용이 많이 들 뿐만 아니라 dense prediction task에 특히 유용한 세분화된 로컬 구조를 약화시킨다. 본 논문은 focal attention에서 영감을 받아 멀티스케일 계층적 컨텍스트 집계를 제안한다. 집계 절차는 두 단계로 구성된다. 즉, 서로 다른 세분성 레벨에서 로컬에서 글로벌 범위까지 컨텍스트를 추출하는 hierarchical contextualization와 서로 다른 세분성 레벨의 모든 컨텍스트 feature를 modulator로 압축하는 gated aggregation이다.
Step 1: Hierarchical Contextualization
입력 feature map $X$가 주어지면 먼저 이를 linear layer $Z^0 = f_z (X) \in \mathbb{R}^{H \times W \times C}$를 사용하여 새로운 feature space에 project한다. 그런 다음 $L$개의 depth-wise convolution 스택을 사용하여 컨텍스트의 계층적 표현을 얻는다. Focal level \(\ell \in \{1, \ldots, L\}\)에서의 출력 $Z^\ell$은 다음과 같다.
\[\begin{equation} Z^\ell = f_a^\ell (Z^{\ell - 1}) = \textrm{GeLU} (\textrm{DWConv} (Z^{\ell - 1})) \in \mathbb{R}^{H \times W \times C} \end{equation}\]여기서 $f_a^\ell$는 커널 크기가 $k^\ell$인 depth-wise convolution $\textrm{DWConv}$와 $\textrm{GeLU}$ activation function을 통해 구현된 $\ell$-번째 레벨의 contextualization function이다. Hierarchical contextualization를 위해 depth-wise convolution을 사용하는 것은 바람직한 속성에 의해 동기가 부여된다. Pooling과 비교하여 depth-wise convolution은 학습 가능하고 구조적이다.
Hierarchical contextualization은 $L$ 레벨의 feature map을 생성한다. $\ell$ 레벨에서 유효 receptive field는
\[\begin{equation} r^\ell = 1 + \sum_{i=1}^\ell (k^\ell − 1) \end{equation}\]이며 이는 커널 크기 $k^\ell$보다 훨씬 크다. 고해상도일 수 있는 전체 입력의 글로벌 컨텍스트를 캡처하기 위해 $L$번째 레벨의 feature map에 global average pooling을 적용한다.
\[\begin{equation} Z^{L+1} = \textrm{Avg-Pool} (Z^L) \end{equation}\]따라서 총 $(L + 1)$개의 feature map \(\{Z^\ell\}_{\ell = 1}^{L+1}\)를 얻는다. 이는 서로 다른 세분성 레벨에서 단거리 및 장거리 컨텍스트를 캡처한다.
Step 2: Gated Aggregation
이 단계에서는 hierarchical contextualization를 통해 얻은 $(L+1)$개의 feature map을 modulator로 압축한다. 이미지에서 시각적 토큰 (query)과 주변 컨텍스트 간의 관계는 콘텐츠 자체에 따라 달라지는 경우가 많다. 예를 들어, 모델은 두드러진 시각적 개체의 query를 인코딩하기 위해 세분화된 로컬 feature에 의존할 수 있지만 배경 장면의 query에는 주로 대략적인 글로벌 feature을 사용할 수 있다. 이러한 직관을 바탕으로 gating 메커니즘을 사용하여 각 query에 대해 다양한 레벨에서 집계할 양을 제어한다. 구체적으로, gating 가중치 \(G = f_g (X) \in \mathbb{R}^{H \times W \times (L+1)}\)을 얻기 위해 linear layer를 사용한다. 그런 다음 element-wise 곱셈을 통해 가중치 합을 수행하여 입력 $X$와 동일한 크기를 갖는 하나의 feature map $Z^\textrm{out}$을 얻는다.
\[\begin{equation} Z^\textrm{out} = \sum_{\ell = 1}^{L+1} G^\ell \odot Z^\ell \in \mathbb{R}^{H \times W \times C} \end{equation}\]여기서 $G^\ell \in \mathbb{R}^{H \times W \times 1}$은 $\ell$ 레벨에 대한 $G$의 슬라이스이다.
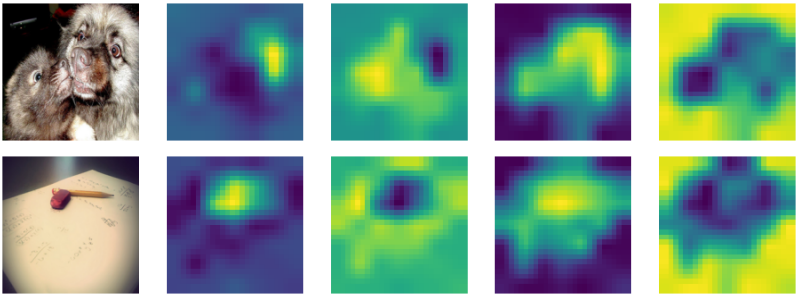
위 그림은 이러한 gating map을 시각화한 것이다. 놀랍게도 FocalNet은 예상대로 적응적으로 다양한 focal level에서 컨텍스트를 수집하는 것을 학습한다. 보다시피, 작은 개체에 대한 토큰의 경우 낮은 focal level에서 세분화된 로컬 구조에 더 중점을 두는 반면, 균일한 배경에 있는 토큰은 더 높은 focal level에서 훨씬 더 큰 컨텍스트를 인식해야 한다. 지금까지 모든 집계는 공간적이었다. 서로 다른 채널을 통한 통신을 활성화하기 위해 다른 linear layer $h(\cdot)$를 사용하여 modulator map $M = h(Z^\textrm{out}) \in \mathbb{R}^{H \times W \times C}$를 얻는다.

위 그림은 FocalNet의 마지막 레이어에서 modulator $M$의 크기를 시각화한 것이다. 흥미롭게도 modulator는 카테고리를 유도하는 객체에 자동으로 더 많은 attention을 기울인다. 이는 FocalNet을 해석하는 간단한 방법을 의미한다.
Focal Modulation
위에서 설명한 $m(\cdot)$의 구현을 고려하면 focal modulation은 토큰 수준에서 다음과 같이 다시 쓸 수 있다.
\[\begin{equation} y_i = q(x_i) \odot h (\sum_{\ell = 1}^{L+1} g_i^\ell \cdot z_i^\ell) \end{equation}\]여기서 $g_i^\ell$과 $z_i^\ell$는 각각 $G^\ell$과 $Z^\ell$의 $i$ 위치에 있는 gating 값과 시각적 feature이다. Algorithm 1은 몇 개의 depth-wise convolution과 linear layer로 focal modulation을 구현한 Pytorch 스타일 pseudo code이다.

3. Relation to Other Architecture Designs
Depth-wise Convolution
Depth-wise convolution은 SA에 대한 로컬 구조 모델링을 강화하거나 순전히 효율적인 장거리 상호 작용을 활성화하는 데 사용되었다. 또한 focal modulation은 depth-wise convolution을 구성 요소 중 하나로 사용한다. 그러나 응답을 출력으로 직접 사용하는 대신 focal modulation은 depth-wise convolution을 사용하여 계층적 컨텍스트를 캡처한 다음 modulaotr로 변환하여 각 query를 변조한다. 이 세 가지 구성 요소는 전체적으로 최종 성능에 기여한다.
Squeeze-and-Excitation (SE)
SE는 ViT가 등장하기 전에 제안되었다. Global average pooling을 활용하여 컨텍스트를 글로벌하게 압축한 다음 MLP와 sigmoid를 사용하여 각 채널에 대한 excitation 스칼라를 얻는다. SE는 focal modulation의 특별한 경우로 간주될 수 있다. $L = 0$으로 설정하면 focal modulation은 SE와 유사한
\[\begin{equation} q(x_i) \odot h(f_g (x_i) \cdot \textrm{Avg-Pool} (f_z (X))) \end{equation}\]로 저하된다. 저자들은 실험에서 이 변형을 연구하고 글로벌 컨텍스트가 시각적 모델링에 훨씬 불충분하다는 것을 발견했다.
PoolFormer
PoolFormer는 최근 소개되었으며, 단순성으로 인해 많은 주목을 받고 있다. Average pooling을 사용하여 sliding window에서 로컬로 컨텍스트를 추출한 다음 element-wise 뺄셈을 사용하여 query 토큰을 조정한다. SE-Net과 유사한 정신을 공유하지만 글로벌 컨텍스트 대신 로컬 컨텍스트를 사용하고 곱셈 대신 뺄셈을 사용한다. 이를 focal modulation과 나란히 놓으면 둘 다 로컬 컨텍스트를 추출하고 query-컨텍스트 상호 작용을 활성화하지만 방식이 다르다는 것을 알 수 있다.
4. Complexity
Focal modulation에는 $Z^0$에 대해 크게 세 가지 linear projection $q(\cdot)$, $h(\cdot)$, $f_z (\cdot)$가 있다. 또한, gating을 위한 경량 선형 함수 $f_g (\cdot)$와 hierarchical contextualization을 위한 $L$개의 depth-wise convolution \(f_a^{\{1, \ldots, L\}}\)가 필요하다. 따라서 학습 가능한 파라미터의 전체 개수는
\[\begin{equation} 3C^2 + C(L + 1) + C \sum_{\ell} (k^\ell)^2 \end{equation}\]이다. $L$과 $(k^\ell)^2$는 일반적으로 $C$보다 훨씬 작기 때문에 모델 크기는 주로 첫 번째 항에 의해 결정된다. 시간 복잡도와 관련하여 linear projection과 depth-wise convolution layer 외에도 element-wise 곱셈은 각 시각적 토큰에 대해 $\mathcal{O} (C(L + 2))$를 도입한다. 따라서 feature map의 전체 복잡도는
\[\begin{equation} \mathcal{O} (HW \times (3C^2 + C(2L + 3) + C \sum_{\ell} (k^\ell)^2)) \end{equation}\]이다. 비교를 해보면, window 크기가 $w$인 Swin Transformer의 window-wise attention은 $\mathcal{O} (HW \times (3C^2 + 2Cw^2))$이고 ViT의 바닐라 self-attention은 $\mathcal{O} ((HW)^2 C + HW \times (3C^2))$이다.
5. Network Architectures
본 논문은 Swin Transformer와 Focal Transformer와 동일한 단계 레이아웃과 hidden 차원을 사용하지만 SA 모듈을 Focal Modulation 모듈로 교체한다. 따라서 일련의 Focal Modulation Network (FocalNet) 변형들을 구성한다. FocalNet에서는 각 레벨의 focal level 수 ($L$)와 커널 크기 ($k^\ell$)만 지정하면 된다. 단순화를 위해 커널 크기를 낮은 focal level에서 높은 focal level로 점진적으로 2씩 늘린다 (ex. $k^{\ell} = k^{\ell - 1} + 2$). Swin Transformer와 Focal Transformer의 복잡도를 일치시키기 위해, 각각 2개와 3개의 focal level을 사용하여 4개의 레이아웃 각각에 대해 작은 receptive field (SRF)와 큰 receptive field (LRF) 버전을 설계하였다. 처음 (커널 크기 = 4$\times$4, stride = 4)과 두 단계들 사이 (커널 크기 = 2$\times$2, stride = 2)에서 패치 임베딩을 위해 non-overlapping convolution layer를 사용한다.
Experiment
1. Image Classification
다음은 ImageNet-1K에서 분류 성능을 비교한 표이다.
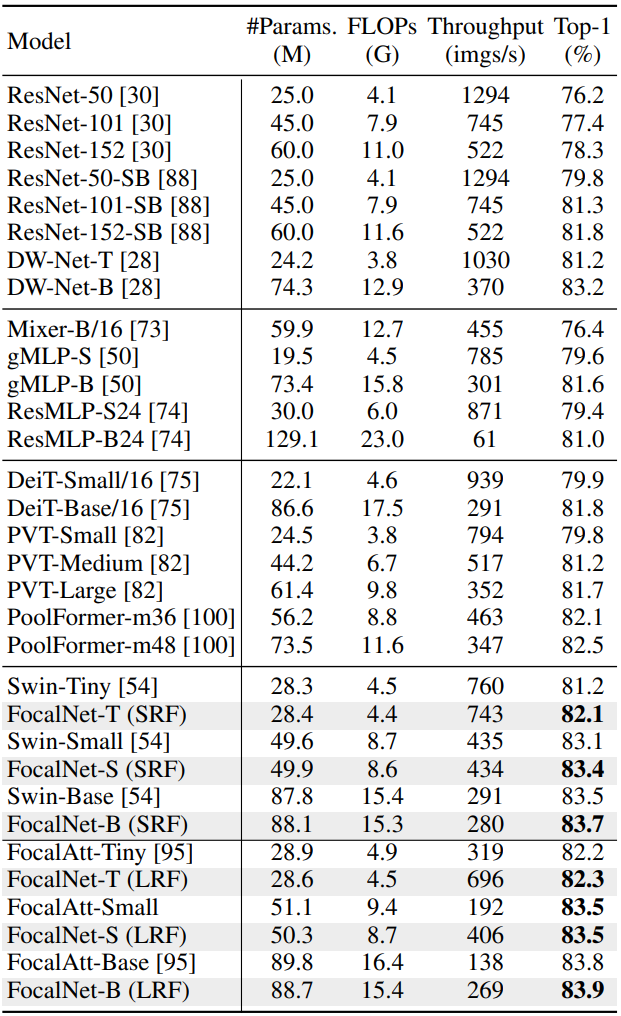
Model augmentation
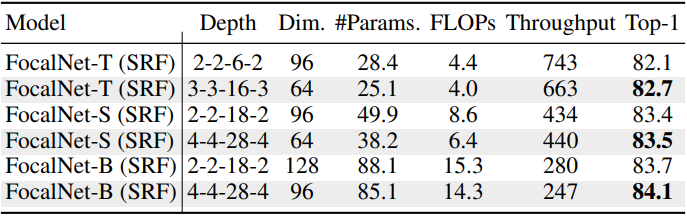
다음은 겹치는 패치 임베딩의 효과를 나타낸 표이다.
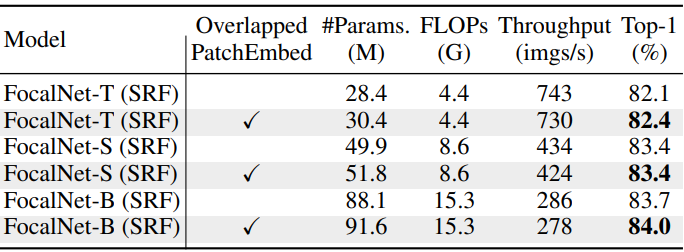
다음은 더 깊고 얇은 네트워크의 효과를 나타낸 표이다.
ImageNet-22K pretraining
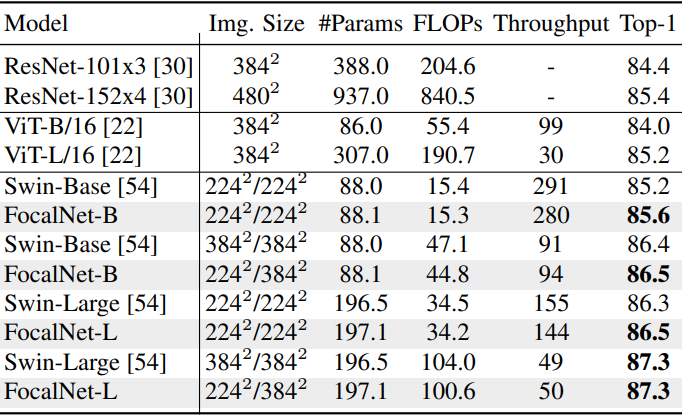
다음은 ImageNet-22K에서 사전 학습한 모델을 ImageNet-1K에서 finetuning한 결과이다.
2. Language-Image Contrast Learning
다음은 ELEVATER 벤치마크에서의 zero-shot 성능을 비교한 표이다.

3. Detection and Segmentation
Object detection and instance segmentation
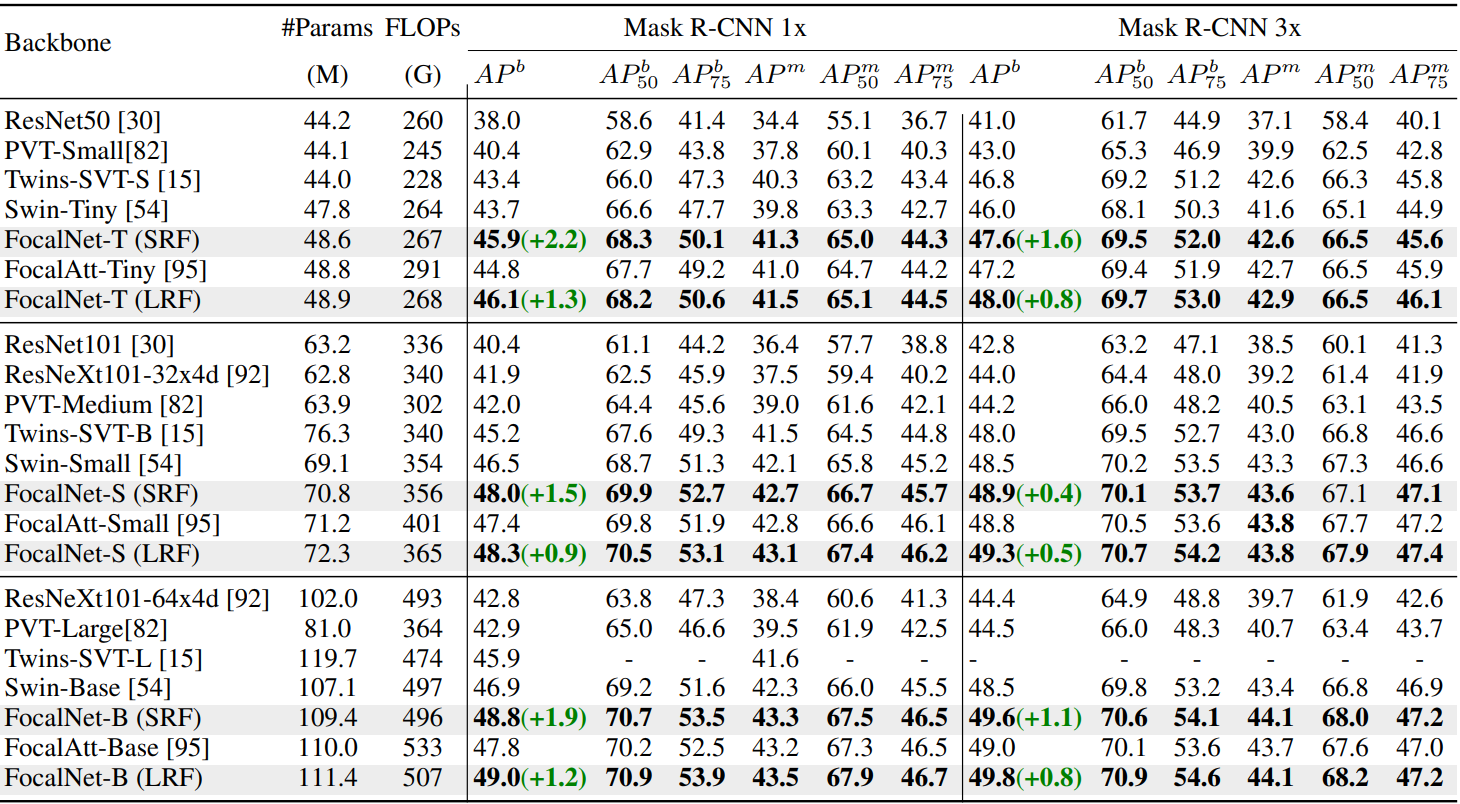
다음은 COCO object detection과 instance segmentation 결과이다.
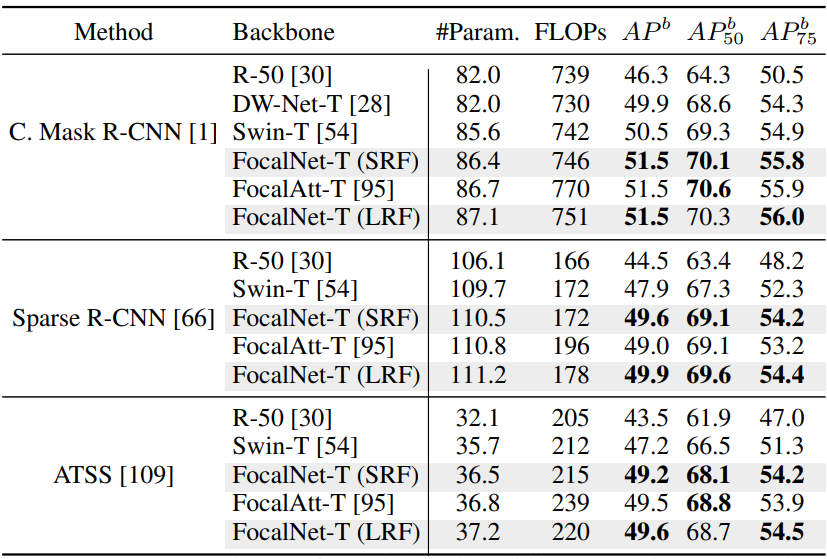
다음은 여러 object detection 방법들과 비교한 표이다.
Semantic Segmentation
다음은 ADE20K에서의 semantic segmentation을 비교한 표이다.
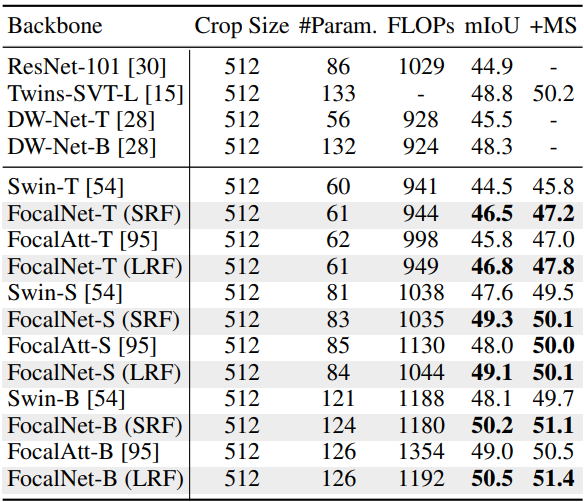
Scaling-up FocalNets
다음은 ADE20K validation set에서의 semantic segmentation을 비교한 표이다.
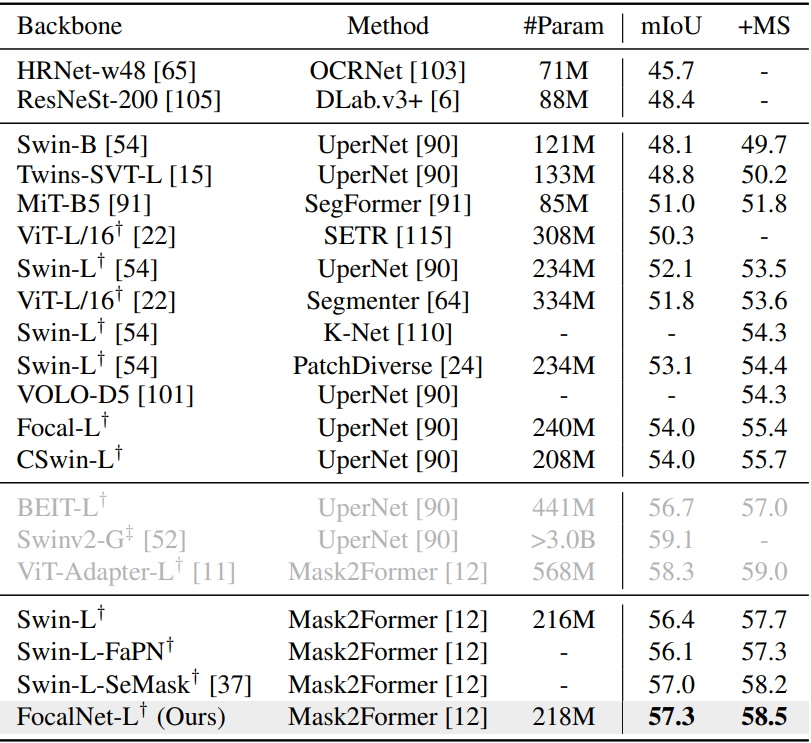
다음은 COCO에서의 panoptic segmentation을 비교한 표이다.
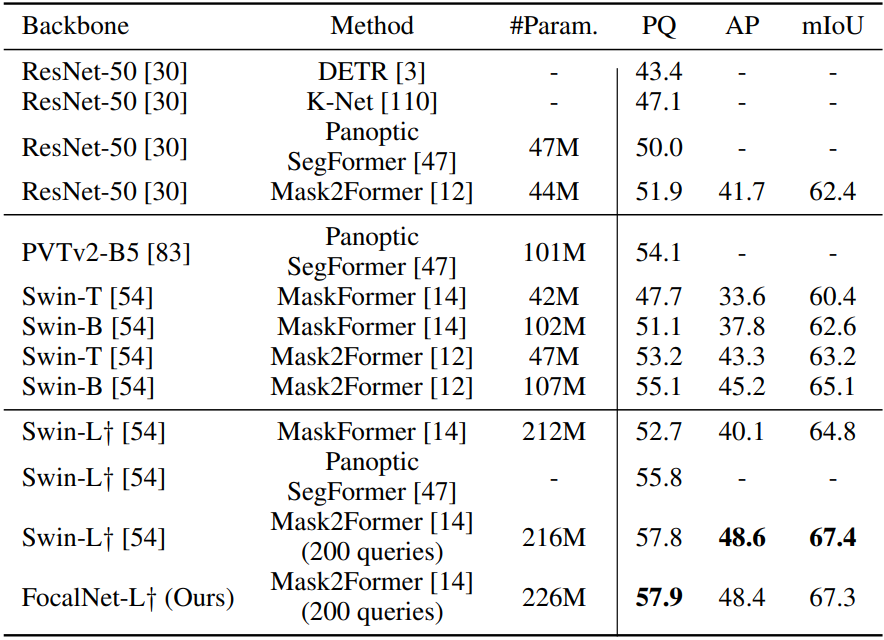
다음은 COCO에서의 최고의 detection model과 비교한 표이다.
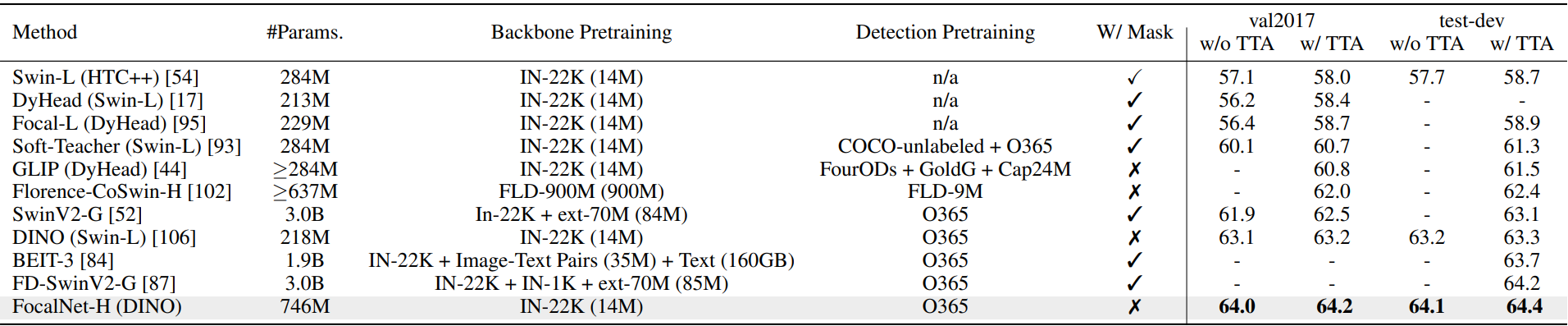
4. Network Inspection
Model Variants
다음은 여러 FocalNet 변형들의 성능을 비교한 표이다.

Component Analysis
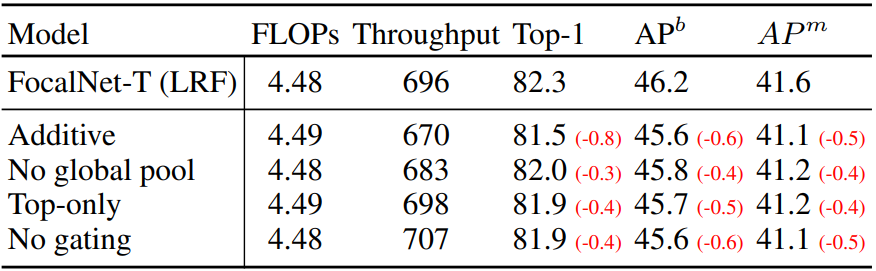
다음은 focal modulation의 구성 요소를 분석한 표이다.
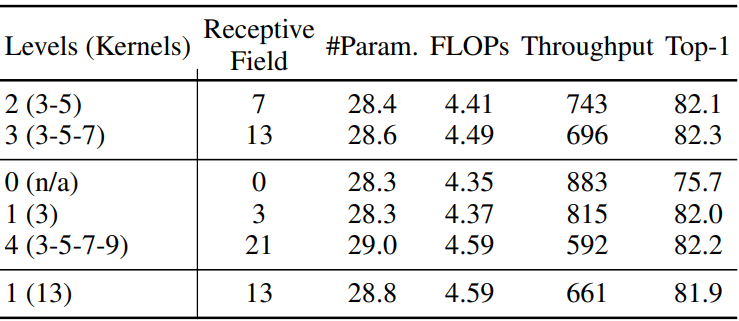
다음은 focal level의 수 $L$에 대한 성능을 비교한 표이다.
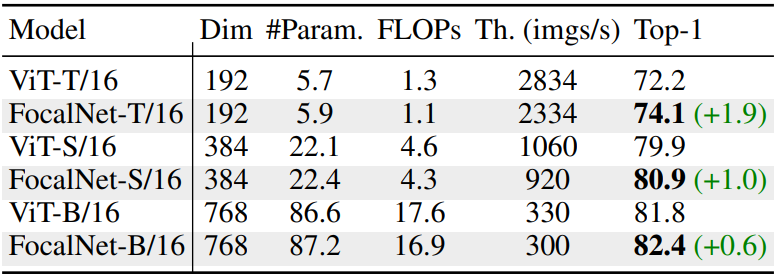
5. Comparisons with ViTs and ConvNeXts
다음은 FocalNet을 ViT와 비교한 표이다.
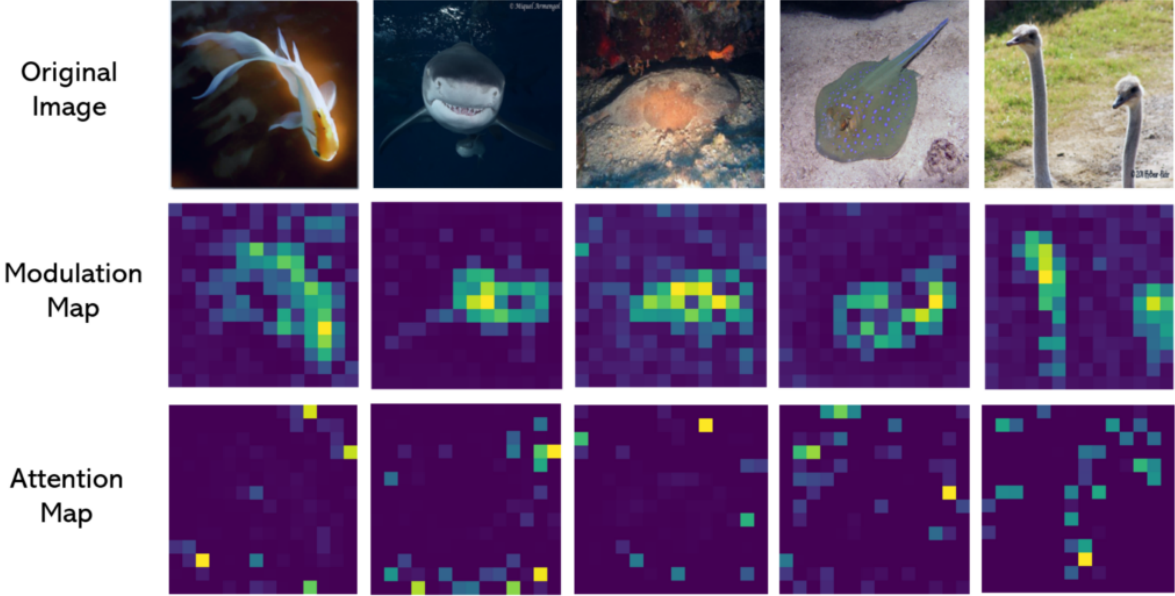
다음은 주어진 이미지에 대한 FocalNet-B/16의 modulation map과 ViT-B/16의 attention map을 비교한 것이다.
다음은 FocalNet을 ConvNeXt과 비교한 표이다.
