[논문리뷰] FlashSplat: 2D to 3D Gaussian Splatting Segmentation Solved Optimally
ECCV 2024. [Paper] [Github]
Qiuhong Shen, Xingyi Yang, Xinchao Wang
National University of Singapore
12 Sep 2024
Introduction
최근 3D Gaussian Splatting (3D-GS)은 3D 공간을 렌더링하고 재구성하는 SOTA 접근 방식으로 등장했다. 3D-GS의 잠재력에도 불구하고, 여전히 2D 마스크에서 3D Gaussian을 분할하는 데에 어려움을 겪고 있다. 이러한 문제에 대한 기존 접근 방식은 3D Gaussian을 레이블링하기 위해 반복적인 gradient descent에 크게 의존했다. 그러나 이러한 방법은 느린 수렴 속도와 최적이 아닌 해에 자주 갇히는 단점이 있어 실시간 성능이나 높은 정확도가 필요한 경우 비실용적이다.
이러한 격차를 해소하기 위해 본 논문은 명시적으로 설계된 간단하지만 전역적으로 최적인 해를 찾는 solver인 FlashSplat을 소개한다. FlashSplat은 재구성된 3D-GS에서 분할된 2D 이미지를 렌더링하는 프로세스가 각 Gaussian의 누적 기여도에 관한 선형 함수로 단순화될 수 있다는 통찰력을 활용한다. 이를 통해 문제를 closed form으로 해결할 수 있는 linear integer programming으로 구성할 수 있으며, splatting 프로세스에 내재된 알파 블렌딩 항에만 의존할 수 있다. 이 발견은 반복적 최적화의 필요성을 우회하고 최적의 레이블 할당으로 직접 이어져 segmentation task를 상당히 간소화한다.
또한, 목적 함수에 background bias를 통합함으로써 3D segmentation에서 2D 마스크 노이즈에 대한 robustness를 더욱 향상시킨다. 이러한 개선은 robustness를 강화할 뿐만 아니라 더 광범위한 장면과 조건에서의 적용성도 강화한다. FlashSplat은 정확도나 global optimality를 희생하지 않고도 약 30초 만에 최적화를 완료하며, 기존 방법보다 50배 더 빠르다.
Method
1. Binary Segmentation as Integer Linear Programming
\(\{G_i\}\)로 재구성된 3DGS 장면으로 시작하며, $L$개의 렌더링된 뷰에 대한 2D binary mask가 \(\{M^v\}\)가 주어진다. 각 마스크 $M \in \mathbb{R}^{H \times W}$은 0 또는 1로 구성되며, 여기서 0은 배경을 나타내고 1은 전경을 나타낸다. 본 논문의 목표는 2D 마스크를 3D 공간으로 projection하여 각 3D Gaussian $G_i$에 0 또는 1이 될 수 있는 3D 레이블 $P_i$를 할당하는 것이다.
이를 위해, 미분 가능한 렌더링 프로세스를 통해 $P_i$를 최적화한다. 목표는 렌더링된 마스크와 제공된 binary mask $M^v$ 사이의 불일치를 최소화하는 것이다. 다행히도 \(\{G_i\}\)가 재구성되면 $\alpha_i$와 $T_i$는 상수가 된다. 따라서 렌더링 함수는 블렌딩하는 속성에 대한 선형 방정식이 된다. 이를 통해 간단한 선형 최적화를 사용하여 최적의 마스크 할당을 풀 수 있는 큰 유연성을 얻을 수 있다.
Segmentation 문제는 다음과 같은 integer linear programming (ILP) 최적화로 공식화될 수 있다.
\[\begin{aligned} \underset{\{P_i\}}{\textrm{Min}} & \; \mathcal{F} = \sum_{v \in L} \sum_{M_{jk}^v \in M^v} \bigg\vert \sum_i P_i \alpha_i T_i - M_{jk}^v \bigg\vert \\ \textrm{subject to} & \; P_i \in \{0, 1\} \end{aligned}\]임의의 $i$에 대한 $\alpha_i \ge 0$와 $T_i \le 1$에 대하여 알파 블렌딩에서 주어진 빛만 흡수될 수 있고, 총 흡수된 빛은 1을 초과할 수 없다. 결과적으로 모든 샘플에서 흡수된 빛의 합은 0과 1 사이로 제한된다. 이를 통해 다음 식이 성립한다.
\[\begin{equation} 0 \le \sum_i P_i \alpha_i T_i \le \sum_i \alpha_i T_i \le 1 \end{equation}\]$M_{jk}^v$는 0 또는 1의 값을 가지므로 $\mathcal{F}$의 절댓값은 $M_{jk}^v$에 따라 달라진다.
\[\begin{equation} \bigg\vert \sum_i P_i \alpha_i T_i - M_{jk}^v \bigg\vert = \begin{cases} \sum_i P_i \alpha_i T_i & \; \textrm{where} \; M_{jk}^v = 0 \\ 1 - \sum_i P_i \alpha_i T_i & \; \textrm{where} \; M_{jk}^v = 1 \end{cases} \end{equation}\]이를 대입하여 $\mathcal{F}$를 정리하면 다음과 같다.
\[\begin{aligned} \mathcal{F} &= \sum_{v,i,j,k} M_{jk}^v + \sum_{v,i,j,k} P_i \alpha_i T_i \mathbb{I} (M_{jk}^v, 0) - \sum_{v,i,j,k} P_i \alpha_i T_i \mathbb{I} (M_{jk}^v, 1) \\ &= \sum_{v,i,j,k} M_{jk}^v + \sum_i P_i (\sum_{v,j,k} \alpha_i T_i \mathbb{I} (M_{jk}^v, 0) - \sum_{v,j,k} \alpha_i T_i \mathbb{I} (M_{jk}^v, 1)) \\ &= C + \sum_i P_i (A_0^i - A_1^i) \end{aligned}\]여기서 $C$, $A_0^i$, $A_1^i$는 상수이며, $\mathbb{I} (\cdot, 0)$과 $\mathbb{I} (\cdot, 0)$는 각각 배경과 전경을 나타내는 indicator function이다.
ILP를 다수결 투표로 해결
마스크 간에 모순이 있는 경우 가중 다수결 투표로 이를 해결한다. 즉, 마스크에서 가장 빈번한 레이블을 기준으로 각 Gaussian $G_i$의 값을 할당한다.
$A_0$와 $A_1$은 각각 배경과 전경을 나타내는 가중 마스크의 수이다. $(A_0 − A_1) > 0$인 경우 $\mathcal{F}$를 최소화하기 위해 $P_i = 0$이 할당되며, $(A_0 − A_1) < 0$인 경우 $P_i = 1$이 할당된다.
\[\begin{equation} P_i = \underset{n}{\arg \max} A_n, \quad n \in \{0, 1\} \\ \textrm{where} \; A_n = \sum_{v,j,k} \alpha_i T_i \mathbb{I} (M_{jk}^v, n) \end{equation}\]직관적으로, 이 최적 할당은 렌더링 중에 개별 3D Gaussian의 기여를 집계하도록 한다. 모든 주어진 마스크에서 전경에 상당히 기여하는 Gaussian은 $P_i = 1$로 전경에 할당되고, 반대로 배경에 주로 기여하는 Gaussian은 $P_i = 0$으로 배경에 할당된다. 또한, 목적 함수 $\mathcal{F}$의 간단한 선형 결합 형태 덕분에 각 3D Gaussian에 동시에 최적의 레이블을 할당할 수 있다.
노이즈 감소를 위한 정규화된 ILP

실제로, 주어진 2D 마스크 세트 \(\{M^v\}\)는 일반적으로 학습된 2D 비전 모델에 의해 예측되며, 이는 특정 영역에 노이즈를 도입할 가능성이 높다. 제공된 2D 마스크의 이러한 특성은 노이즈가 많은 3D segmentation 결과로 이어질 수 있다.
이를 해결하기 위해 위의 최적 할당을 개선한다. 먼저, L1 정규화를 통해 Gaussian의 전체 기여도를 처음에 정규화한다.
\[\begin{equation} \bar{A}_e = \frac{A_e}{\sum_t A_t} \end{equation}\]그런 다음 background bias $\gamma \in [-1, 1]$를 도입하여
\[\begin{equation} \hat{A}_0 = \bar{A}_0 + \gamma \end{equation}\]로 재보정하고, 이를 통해 최적 할당을
\[\begin{equation} P_i = \underset{n}{\arg \max} \{ \hat{A}_0, \bar{A}_1 \} \end{equation}\]로 조정한다. $\gamma > 0$을 사용하면 분할 결과에서 노이즈가 효과적으로 줄어든다. 반대로 $\gamma < 0$은 배경이 더 깨끗해진다. 이 완화된 형태의 최적 할당은 다양한 다운스트림 task에 대한 정확한 3D segmentation 결과를 생성하는 유연성을 제공한다.
2. From Binary to Scene Segmentation
3D 장면의 다양한 뷰에 걸쳐 수많은 인스턴스가 존재한다. 이러한 장면 내에서 여러 물체를 분할하려면 위의 방법에 따라 binary segmentation을 여러 번 실행해야 하며, 이는 본질적으로 장면 분할의 속도를 늦춘다. 따라서 보다 효율적으로 해결하기 위해 방법론을 장면 분할로 확장한다.
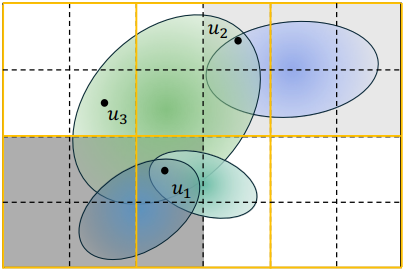
Multi-instance segmentation로의 이러한 전환은 두 가지 주요 고려 사항에서 비롯된다.
- 3D Gaussian이 하나의 물체에만 속하는 것이 아니다. 위 그림에서 볼 수 있듯이, 픽셀 $u_1$과 $u_2$는 서로 다른 물체에 속함에도 불구하고 동일한 3D Gaussian의 영향을 받는다.
- 여러 인스턴스를 도입하면 \(P_i \in \{0, \ldots, E − 1\}\)에 대한 $\mathcal{F}$의 제약 조건이 복잡해진다 ($E$는 장면의 총 인스턴스 수). 제공된 마스크의 집합 $M^v$도 \(M^v \in \{0, \ldots, E − 1\}\)이 된다. 이러한 제약 조건은 인스턴스 간 레이블이 교환될 수 있으므로 global optimum을 달성하지 못한다.
이러한 과제를 해결하기 위해 multi-instance segmentation을 binary segmentation의 조합으로 재해석하여 최적 할당 전략을 수정한다. 3D 장면에서 레이블이 $e$인 특정 인스턴스를 분리하기 위해 인스턴스 집합 내의 다른 모든 물체를 배경으로 재정의하여 \(A_\textrm{others}\)를 계산한다.
\[\begin{aligned} P_i &= \underset{n}{\arg \max} A_n, \quad n \in \{0, t\} \\ \textrm{where} \; A_t &= \sum_{v,j,k} \alpha_i T_i \mathbb{I} (M_{jk}^v, t), \\ A_0 &= A_\textrm{others} = \sum_{e \ne t} \sum_{v,j,k} \alpha_i T_i \mathbb{I} (M_{jk}^v, e) \end{aligned}\]이 공식을 사용하면 집합 \(\{A_e\}\)를 한 번만 누적한 다음 이 집합에 대해 argmax를 수행하여 각 물체 $e$에 대한 Gaussian 부분집합 \(\{G_i\}_e\)를 얻을 수 있다. 결과적으로 물체의 ID를 지정하여 3D Gaussian의 부분집합을 선택적으로 제거하거나 수정할 수 있다. 또한 $\gamma < 0$일 때 다른 인스턴스의 부분집합이 겹칠 수 있으며, 이는 3D-GS의 고유한 비배타적 특성을 반영한 것이다.
3. Depth-guided Novel View Mask Rendering

위의 공식은 dense한 최적화의 필요성을 회피하므로, 마스크된 2D 뷰의 약 10%만을 사용하여 robust한 분할 결과를 얻을 수 있다. 또한 FlashSplat은 이전에 보지 못한 뷰에 대한 2D 마스크 \(\hat{M}^v\)를 생성하는 기능을 제공한다. Binary segmentation에서 새로운 뷰 마스크 렌더링의 경우, 단순히 $P_i = 1$인 전경 Gaussian을 렌더링하여 각 픽셀에 대한 누적 알파 값 $\rho_{jk}$를 생성한 다음, 미리 정의된 threshold $\tau$를 사용하여 2D 마스크를 얻을 수 있다.
동일한 시점에서 각 물체의 연관된 3D Gaussian 부분집합 \(\{G_i\}_e\)를 렌더링하면 여러 물체가 조건 \(\rho_{jk}^e > \tau\)를 충족할 수 있다. 이 경우 최종 분할 결과를 결정하기 위해 깊이를 도입한다. 각 픽셀 위치 $(j, k)$의 깊이는 최종 2D 마스크 결과를 필터링하는 데 사용된다. 주어진 픽셀 $(j, k)$에서 깊이 값이 가장 작은 물체 $e$가 \(\hat{M}_{jk} = e\)로 선택된다.
Experiments
1. 3D segmentation results
다음은 3D segmentation의 예시이다.

2. Object Inpainting
다음은 물체 제거 후 inpainting한 예시이다.

3. Quantitative comparison
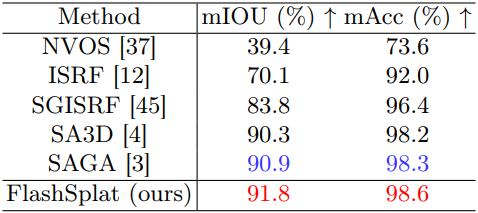
다음은 NVOS 데이터셋에서 정량적으로 비교한 표이다.
4. Computation cost
다음은 계산 비용을 비교한 표이다. (Figurines 장면)

5. Ablation study
다음은 SAM에서 예측한 2D 마스크와 이를 이용한 FlashSplat의 3D segmentation 결과를 비교한 것이다.

다음은 더 적은 마스크를 사용한 3D segmentation 결과를 비교한 것이다.
