[논문리뷰] eDiff-I: Text-to-Image Diffusion Models with an Ensemble of Expert Denoisers

arXiv 2022. [Paper] [Page]
Yogesh Balaji, Seungjun Nah, Xun Huang, Arash Vahdat, Jiaming Song, Karsten Kreis, Miika Aittala, Timo Aila, Samuli Laine, Bryan Catanzaro, Tero Karras, Ming-Yu Liu
NVIDIA Corporation
2 Nov 2022

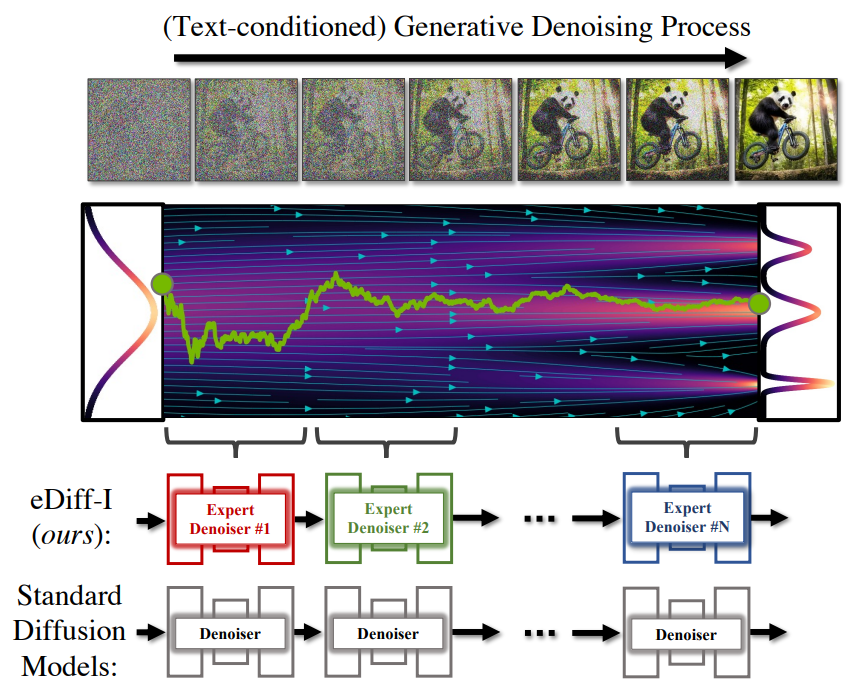
Introduction

반복적인 denoising을 통해 이미지를 생성하는 diffusion model은 이미지 생성 분야를 혁신하고 있다. 이들은 최근 text-to-image 모델의 핵심 building block으로, 보지 못한 새로운 개념에 대해서도 복잡한 텍스트 프롬프트를 사실적인 이미지로 바꾸는 놀라운 능력을 보여주었다. 틀림없이 이러한 성공은 주로 diffusion model의 뛰어난 확장성에 기인한다. 확장성은 더 큰 모델 용량, 컴퓨팅, 데이터셋을 더 나은 이미지 생성 품질로 변환할 수 있는 명확한 경로를 제공하기 때문이다. 이것은 장기간에 걸쳐 대규모 컴퓨팅 성능을 갖춘 방대한 데이터에 대해 학습된 확장 가능한 모델이 종종 수작업으로 제작된 전문 모델보다 성능이 우수하다는 씁쓸한 교훈을 상기시켜 준다.

저자들은 text-to-image 생성 task를 위한 모델 능력 측면에서 diffusion model을 확장하는 데 관심이 있다. 먼저 각 denoising step에 대해 더 깊거나 더 넓은 신경망을 사용하여 용량을 늘리면 샘플링의 테스트 시간 계산 복잡성에 부정적인 영향을 미친다. 이는 샘플링이 denoising network가 여러 번 호출되는 역 미분 방정식을 푸는 것과 같기 때문이다. 본 논문은 테스트 시간 계산 복잡성 오버헤드를 발생시키지 않고 확장 목표를 달성하는 것을 목표로 한다.

본 논문의 핵심 통찰력은 text-to-image diffusion model이 생성 중에 흥미로운 시간 역학을 나타낸다는 것이다. 초기 샘플링 단계에서 denoising network에 대한 입력 데이터가 random noise에 더 가까울 때 diffusion model은 주로 텍스트 프롬프트에 의존하여 샘플링 프로세스를 guide한다. 생성이 계속됨에 따라 모델은 시각적 feature로 점차 shift하여 이미지를 denoise하고 대부분 입력 텍스트 프롬프트를 무시한다.

저자들은 이 관찰로부터 동기를 부여받아 생성 프로세스의 특정 단계에 특화된 expert denoiser의 앙상블을 학습하여 diffusion model의 용량을 늘릴 것을 제안한다. 이것은 timestep당 샘플링의 계산 복잡성을 증가시키지 않지만, 여러 denoising model이 서로 다른 단계에 대해 학습되어야 하기 때문에 학습 복잡성을 증가시킨다. 이를 해결하기 위해 저자들은 모든 단계에 대해 공유 diffusion model을 사전 학습할 것을 제안한다. 그런 다음 이 사전 학습된 모델을 사용하여 특수 모델을 초기화하고 더 적은 수의 iteration을 위해 fine-tuning한다.

또한 사전 학습된 텍스트 인코더의 앙상블을 사용하여 text-to-image model에 입력을 제공하는 방법도 살펴본다. 텍스트 임베딩을 해당 이미지 임베딩에 맞도록 학습된 CLIP 텍스트 인코더와 언어 모델링 task를 위해 학습된 T5 텍스트 인코더를 모두 사용한다. 이전 연구에서는 이 두 인코더를 사용했지만 하나의 모델에서 함께 사용된 적은 없다. 이 두 인코더는 서로 다른 목적으로 학습되기 때문에 임베딩은 동일한 입력 텍스트로 서로 다른 이미지의 형성을 선호한다. CLIP 텍스트 임베딩은 생성된 이미지의 전체적인 모양을 결정하는 데 도움이 되지만 출력은 텍스트의 세밀한 디테일을 놓치는 경향이 있다. 대조적으로 T5 텍스트 임베딩만으로 생성된 이미지는 텍스트에 설명된 개별 개체를 더 잘 반영하지만 전체 모양은 덜 정확하다. 이들을 공동으로 사용하면 모델에서 최상의 이미지 생성 결과를 얻을 수 있다. 텍스트 임베딩 외에도 style transfer에 유용한 입력 이미지의 CLIP 이미지 임베딩을 활용하도록 모델을 학습한다. 이 전체 모델을 ensemble diffusion for images (eDiff-I)라고 부른다.

텍스트 프롬프트는 생성된 이미지에 포함할 개체를 지정하는 데 효과적이지만 텍스트를 사용하여 개체의 공간 위치를 제어하는 것은 번거롭다. 저자들은 사용자가 캔버스에 낙서를 함으로써 특정 객체와 개념의 위치를 지정할 있도록 하는 text-to-image model로 제어 가능한 생성 접근 방식인 paint-with-words를 위해 학습이 필요 없는 모델의 확장을 고안한다. 그 결과 텍스트와 semantic mask를 입력으로 사용하여 사용자가 완벽한 이미지를 만드는 데 더 나은 도움을 줄 수 있는 이미지 생성 모델이 탄생했다.

Background

Text-to-image 생성 모델에서 입력 텍스트는 종종 CLIP 또는 T5 텍스트 인코더와 같은 사전 학습된 모델에서 추출된 텍스트 임베딩으로 표현된다. 이 경우 텍스트 프롬프트가 주어진 이미지를 생성하는 문제는 텍스트 임베딩을 입력 조건으로 사용하고 조건에 맞는 이미지를 생성하는 조건부 생성 모델을 학습하는 것으로 귀결된다.

Text-to-image diffusion model은 noise 분포에서 이미지를 샘플링하고 denoising model $D(x; e, \sigma)$를 사용하여 반복적으로 denoise하여 데이터를 생성한다. 여기서 $x$는 현재 step의 noisy한 이미지를 나타내고 $e$는 입력 임베딩이다. $\sigma$는 현재 noise level을 나타내는 스칼라 입력이다.

Training

Denoising model은 다양한 스케일의 Gaussian noise를 추가하여 손상된 깨끗한 이미지를 복구하도록 학습되었다. EDM의 공식과 제안된 schedule에 따라 목적 함수를 다음과 같이 쓸 수 있다.

\[\begin{equation} \mathbb{E}_{p_\textrm{data} (x_\textrm{clean}, e), p(\epsilon), p(\sigma)} [\lambda (\sigma) \| D (x_\textrm{clean} + \sigma \epsilon; e, \sigma) - x_\textrm{clean} \|_2^2 ] \end{equation}\]

$p(\epsilon) = \mathcal{N}(0,1)$이고 $p(\sigma)$는 noise level이 샘플링될 분포, $\lambda(\sigma)$는 loss weighting factor이다.

Denoiser formulation

EDM 논문을 따라 denoiser를 다음과 같이 컨디셔닝할 수 있다.

\[\begin{equation} D(x; e, \sigma) := \bigg( \frac{\sigma_\textrm{data}}{\sigma^\ast} \bigg)^2 x + \frac{\sigma \cdot \sigma_\textrm{data}}{\sigma^\ast} F_\theta \bigg( \frac{x}{\sigma^\ast}; e, \frac{\ln (\sigma)}{4} \bigg), \\ \sigma^\ast = \sqrt{\sigma^2 + \sigma_\textrm{data}^2}, \quad \ln (\sigma) \sim \mathcal{N} (P_\textrm{mean}, P_\textrm{std}) \end{equation}\]

$F_\theta$는 학습된 신경망이며, $\sigma_\textrm{data} = 0.5$를 자연 이미지 픽셀 값의 표준 편차를 위한 근사값으로 사용한다. $P_\textrm{mean} = -1.2$과 $P_\textrm{std} = 1.2$로 둔다.

\[\begin{equation} \lambda(\sigma) = \bigg( \frac{\sigma^\ast}{\sigma \cdot \sigma_\textrm{data}} \bigg)^2 \end{equation}\]

로 두어 $F_\theta$의 출력 가중치를 상쇄시킨다.

Sampling

Diffusion model을 사용하여 이미지를 생성하기 위해 사전 확률 분포 $x \sim \mathcal{N} (0, \sigma_\textrm{max}^2 I)$에서 샘플링하여 초기 이미지를 생성한 후, 다음과 같은 생성 ODE를 $\sigma_\textrm{max}$부터 $\sigma_\textrm{min} \approx 0$까지 푼다.

\[\begin{equation} \frac{dx}{d \sigma} = - \sigma \nabla_x \log p (x \vert e, \sigma) = \frac{x - D(x; e, \sigma)}{\sigma} \end{equation}\]

위에서 $\nabla_x \log p (x \vert e, \sigma)$는 손상된 데이터의 score function이며 denoising model로부터 얻을 수 있다.

Super-resolution diffusion models

Text-conditioned super-resolution diffusion model의 학습은 위에서 설명한 text-conditioned diffusion model의 학습을 대체로 따른다. 주요 차이점은 super-resolution denoising model은 저해상도 이미지도 컨디셔닝 입력으로 사용한다는 것이다. 이전 연구에 이어 super-resolution model의 일반화 능력을 향상시키기 위해 학습 중에 저해상도 입력 이미지에 다양한 손상을 적용한다.

Ensemble of Expert Denoisers

앞서 설명했듯이, text-to-image diffusion model은 denoising model에 의존하여 가우시안 분포의 샘플을 입력 텍스트 프롬프트로 컨디셔닝된 이미지로 변환한다. 생성 ODE는 $D(x; e, \sigma)$를 사용하여 샘플을 입력 컨디셔닝에 맞는 이미지 쪽으로 점진적으로 guide한다.

각 noise level $\sigma$에서 denoising model $D$는 현재 noisy한 입력 이미지 $x$와 입력 텍스트 프롬프트 $e$에 의존한다. 저자들의 주요 관찰은 text-to-image diffusion model이 이 두 소스에 의존하면서 고유한 시간 역학을 나타낸다는 것이다. 생성 초기에 $\sigma$가 클 때 입력 이미지 $x$는 대부분 noise를 포함한다. 따라서 입력된 시각적 콘텐츠에서 직접 denoise하는 것은 어렵고 모호한 task이다. 이 단계에서 $D$는 주로 입력 텍스트 임베딩에 의존하여 텍스트에 맞는 이미지에 대한 방향을 추론한다. 그러나 생성이 끝날 무렵 $\sigma$가 작아짐에 따라 대부분의 거친 레벨의 콘텐츠는 denoising model에 의해 그려진다. 이 단계에서 $D$는 대부분 텍스트 임베딩을 무시하고 세분화된 디테일을 추가하기 위해 시각적 feature를 사용한다.

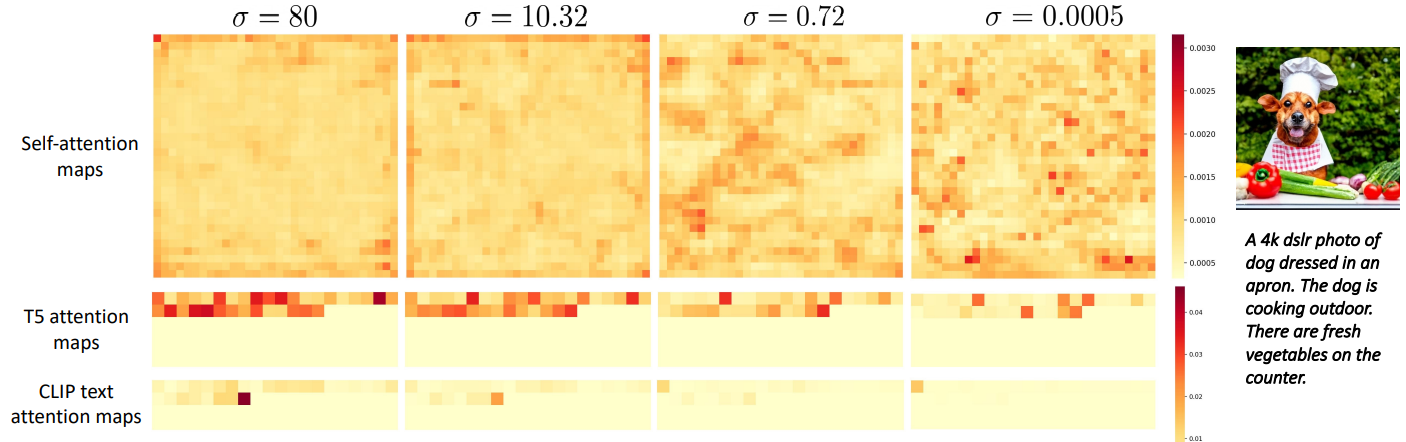
저자들은 위 그림에서 서로 다른 생성 단계의 시각적 feature에 대한 self-attention map과 비교하여 시각적 feature와 텍스트 feature 간의 cross-attention map을 시각화하여 이 관찰을 검증한다.

위 그림에서는 denoising process의 여러 단계에서 입력 캡션을 한 프롬프트에서 다른 프롬프트로 전환할 때 생성된 샘플이 어떻게 변경되는지 추가로 검사한다. Denoising의 마지막 7%에서 프롬프트가 바뀌면 생성 출력은 동일하게 유지된다. 반면에 학습의 처음 40%에서 프롬프트가 바뀌면 출력이 완전히 변경된다.

Diffusion model에 대한 대부분의 기존 연구에서 denoising model은 모든 noise level에서 공유되며 시간 역학은 MLP 네트워크를 통해 모델에 공급되는 간단한 time embedding을 사용하여 표현된다. 저자들은 제한된 용량의 공유 모델을 사용하여 데이터에서 denoising diffusion의 복잡한 시간 역학을 효과적으로 학습하지 못할 수 있다고 주장한다. 대신, expert denoiser의 앙상블을 도입하여 denoising model의 용량을 확장할 것을 제안한다. 각 expert denoiser는 특정 범위의 noise level에 특화된 denoising model이다. 이렇게 하면 각 noise level에서 $D$를 평가하는 계산 복잡성이 동일하게 유지되므로 샘플링 속도를 늦추지 않고 모델 용량을 늘릴 수 있다.

그러나 서로 다른 단계에 대해 별도의 denoising model을 naive하게 학습시키면 각 expert denoiser를 처음부터 학습시켜야 하므로 학습 비용이 크게 증가할 수 있다. 이를 해결하기 위해 먼저 모든 noise level에서 공유 모델을 학습한다. 그런 다음 이 모델을 사용하여 denoising expert를 초기화한다.

1. Efficient Training of Expert Denoisers

Expert denoiser를 효율적으로 학습시키기 위해 binary tree 구현을 기반으로 한 분기 전략을 제안한다. $p(\sigma)$로 표시되는 전체 noise level 분포를 사용하여 모든 noise level에서 공유되는 모델을 학습하는 것으로 시작한다. 그런 다음 이 기본 모델에서 두 expert를 초기화한다. 이 모델은 binary tree의 첫 번째 레벨에서 학습되었으므로 level 1 experts라고 부른다. 이 두 expert는 $p(\sigma)$를 면적별로 동일하게 분할하여 얻은 noise 분포 $p_0^1 (\sigma)$와 $p_1^1(\sigma)$에 대해 학습한다. 따라서 $p_0^1(\sigma)$에 대해 학습한 expert는 낮은 noise level에 특화되어 있고 $p_1^1(\sigma)$에 대해 학습한 expert는 높은 noise level에 특화되어 있다. 구현에서는 $p(\sigma)$가 로그 정규 분포를 따른다.

Level 1 expert model이 학습되면 위에서 설명한 것과 유사한 방식으로 각각의 해당 noise interval을 분할하고 각 interval에 대해 expert를 학습한다. 이 프로세스는 여러 레벨에 대해 재귀적으로 반복된다. 일반적으로 레벨 $l$에서 노이즈 분포 $p(\sigma)$를 \(\{p_i^l (\sigma)\}_{i=0}^{2^l−1}\)로 주어진 동일한 영역의 $2^l$ interval로 분할하고 모델 $i$는 분포 $p_i^l (\sigma)$에서 학습된다. Binary tree에서 이러한 모델 또는 노드를 $E_i^l$라고 부른다.

이상적으로는 각 레벨 $l$에서 $2^l$개의 모델을 학습해야 한다. 그러나 binary tree의 깊이에 따라 모델 크기가 기하급수적으로 증가하므로 이는 실용적이지 않다. 또한 저자들은 실제로 많은 중간 interval에서 학습된 모델이 최종 시스템의 성능에 크게 기여하지 않는다는 사실을 발견했다. 따라서 binary tree의 각 레벨에서 가장 왼쪽 노드 $E_0^l$와 가장 오른쪽 노드 $E_{2^l-1}^l$에서 트리를 성장시키는 데 주로 중점을 둔다. 가장 오른쪽 interval에는 noise level이 높은 샘플이 포함된다.

앞서 본 두 그림에서 볼 수 있듯이, 이 영역에서 핵심 이미지 형성이 발생하기 때문에 텍스트 컨디셔닝을 개선하려면 높은 noise level에서 우수한 denoising이 중요하다. 따라서 이 체제에서 전용 모델을 갖는 것이 바람직하다. 유사하게, denoising의 최종 step이 샘플링 중에 이 영역에서 발생하므로 더 낮은 noise level에서 모델을 학습시키는 데에도 중점을 둔다. 따라서 날카로운 결과를 얻으려면 좋은 모델이 필요하다. 마지막으로 두 개의 극단적인 interval 사이에 있는 모든 중간 noise interval에서 하나의 모델을 학습시킨다.

간단히 말해서, 최종 시스템은 3개의 expert denoiser로 구성된 앙상블을 갖게 된다.

1. 낮은 noise level에 초점을 맞춘 expert denoiser (binary tree의 가장 왼쪽 interval로 학습)
2. 높은 noise level에 초점을 맞춘 expert denoiser (binary tree의 가장 오른쪽 interval로 학습)
3. 모든 중간 noise interval을 학습하기 위한 단일 expert denoiser

2. Multiple Conditional Inputs

Text-to-image diffusion model을 학습시키기 위해 학습 중에 다음과 같은 조건부 임베딩을 사용한다.

1. T5-XXL 텍스트 임베딩
2. CLIP L/14 텍스트 임베딩
3. CLIP L/14 이미지 임베딩

실시간으로 계산하는 것은 비용이 많이 들기 때문에 전체 데이터셋에 대해 이러한 임베딩을 미리 계산해 둔다. 이전 연구와 유사하게 time embedding에 project된 조건부 임베딩을 추가하고 denoising model의 여러 해상도에서 추가로 cross-attention을 수행한다. 학습 중에 이러한 각 임베딩에 대해 독립적으로 random dropout을 사용하며, 임베딩이 drop되면 전체 임베딩 텐서를 0으로 만든다. 3개의 임베딩이 모두 drop되면 unconditional한 학습에 해당하므로 classifier-free guidance를 수행하는 데 유용하다. 아래 그림에서 입력 컨디셔닝 체계를 시각화한다.

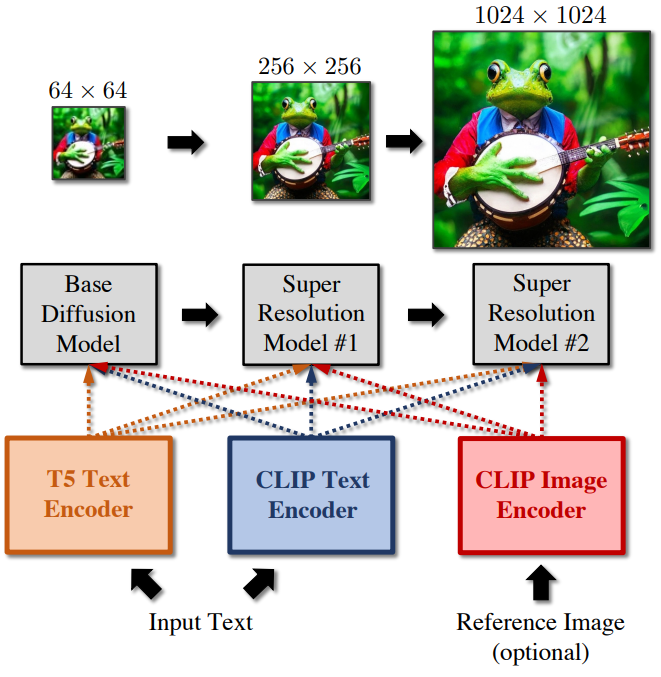
완전한 파이프라인은 일련의 diffusion model로 구성된다. 특히, 64$\times$64 해상도의 이미지를 생성할 수 있는 base model과 이미지를 각각 256$\times$256 및 1024$\times$1024 해상도로 점진적으로 upsampling할 수 있는 2개의 super-resolution diffusion model이 있다. Super-resolution model을 학습시키기 위해 random degradation로 손상된 ground-truth 저해상도 입력을 조건으로 한다. 학습 중에 degradation을 추가하면 모델이 base model에서 생성된 출력에 존재할 수 있는 아티팩트를 제거하기 위해 더 잘 일반화할 수 있다. Base model의 경우 Diffusion models beat GANs on image synthesis 논문에서 제안한 U-net 아키텍처의 수정된 버전을 사용한다. Super-resolution model 경우 Efficient U-net 아키텍처의 수정된 버전을 사용한다.

3. Paint-with-words

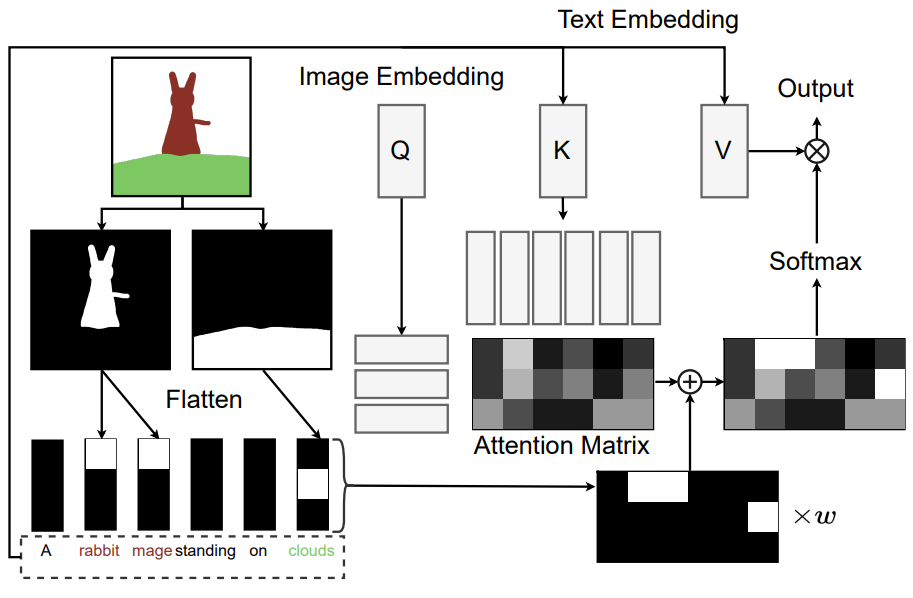
저자들은 사용자가 객체의 공간적 위치를 지정할 수 있는 paint-with-words라는 학습이 필요 없는 방법을 제안한다. 위 그림과 같이 사용자는 텍스트 프롬프트에서 임의의 문구를 선택하고 캔버스에 낙서하여 해당 문구에 해당하는 이진 마스크를 만들 수 있다. 마스크는 모든 cross-attention layer에 입력되며 각 layer의 해상도와 일치하도록 bilinearly downsampling된다.

이러한 마스크를 사용하여 입력 attention 행렬 $A \in \mathbb{R}^{N_i \times N_t}$를 생성한다. 여기서 $N_i$와 $N_t$는 각각 이미지와 텍스트 토큰의 수다. $A$의 각 열은 해당 열의 텍스트 토큰을 포함하는 구(phrase)에 해당하는 마스크를 flattening하여 생성된다. 해당 텍스트 토큰이 사용자가 선택한 문구에 포함되어 있지 않으면 열이 0으로 설정된다. $A$를 cross-attention layer의 원래 attention 행렬에 추가한다. 이제 출력을

\[\begin{equation} \textrm{softmax} \bigg( \frac{QK^\top + wA}{\sqrt{d_k}} \bigg) V \end{equation}\]

로 계산한다. 여기서 $Q$는 이미지 토큰의 query embedding이고, $K$와 $V$는 텍스트 토큰의 key embedding과 value embedding이다. $d_k$는 $Q$와 $K$의 차원이고 $w$는 사용자 입력 attention의 강도를 제어하는 스칼라 가중치다. 사용자가 어떤 영역에 구(phrase)를 그리면 해당 영역의 이미지 토큰이 해당 구(phrase)에 포함된 텍스트 토큰에 더 많이 참여하도록 권장된다. 결과적으로 해당 구문에 해당하는 의미 개념이 지정된 영역에 나타날 가능성이 더 높다.

저자들은 더 높은 noise level에서 더 큰 가중치를 사용하고 $A$의 영향을 $Q$와 $K$의 스케일과 무관하게 만드는 것이 유익하다는 것을 발견했다. 이는 경험적으로 잘 작동하는 다음과 같은 schedule로 작동한다.

\[\begin{equation} w = w' \cdot \log (1 + \sigma) \cdot \max (QK^\top) \end{equation}\]

$w’$는 사용가 정하는 스칼라이다.

Experiment

• Optimization: AdamW optimizer (learning rate = 0.0001), weight decay 0.01, batch size 2048
• Datasets
  • 사전 학습된 CLIP model로 CLIP score를 측정하여 임계값을 넘지 못하는 이미지-텍스트 쌍은 제거
  • Base model과 SR256 model은 resize-central crop 적용
  • SR1024 model은 256$\times$256 영역을 random crop

1. Main Results

다음은 COCO 2014 validation 데이터셋에서 최근 state-of-the-art 방법과 Zero-shot FID을 비교한 표이다.

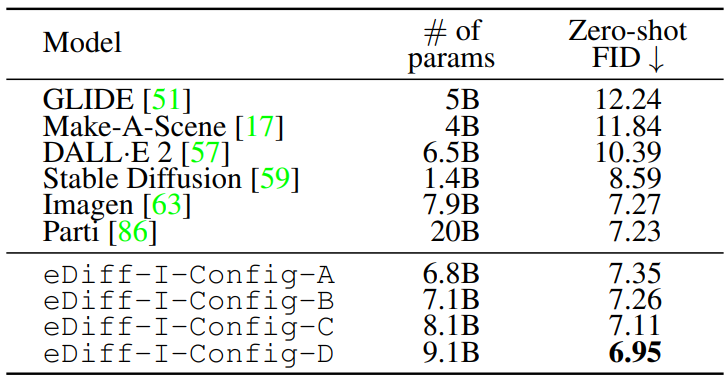
각 모델의 설정은 다음과 같다.

• eDiff-I-Config-A: Base model은 baseline model. Baseline SR256 model로 upsampling.
• eDiff-I-Config-B: Base model은 baseline model. 2개의 expert $E_0^1$과 $E_1^1$로 구성된 ensemble SR256 model로 upsampling.
• eDiff-I-Config-C: $E_511^9$로 학습된 expert와 $E_511^9$를 제외하고 학습된 expert로 구성된 2-expert ensemble base model. SR model은 B와 동일.
• eDiff-I-Config-D: $E_511^9$로 학습된 expert, $E_0^3$으로 학습된 expert, 나머지로 학습된 expert로 구성된 3-expert ensemble base model. SR model은 B와 동일.

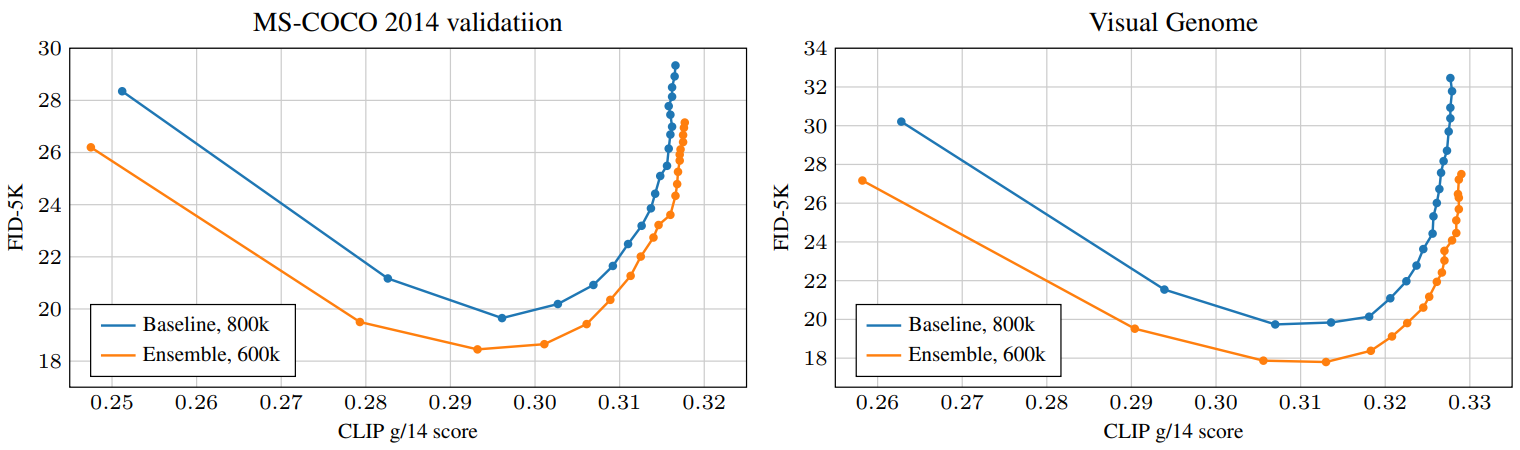
다음은 2-Expert-Ensemble model과 baseline model를 비교한 그래프이며, classifier-free guidance 강도를 0에서 10까지 0.5 간격으로 바꿔가며 plot한 것이다.

다음은 2-Expert-Ensemble model과 baseline model를 비교한 예시 샘플이다.

다음은 모델의 파라미터 수를 증가시킬 때 단일 feed-forward 시간을 비교한 그래프이다.

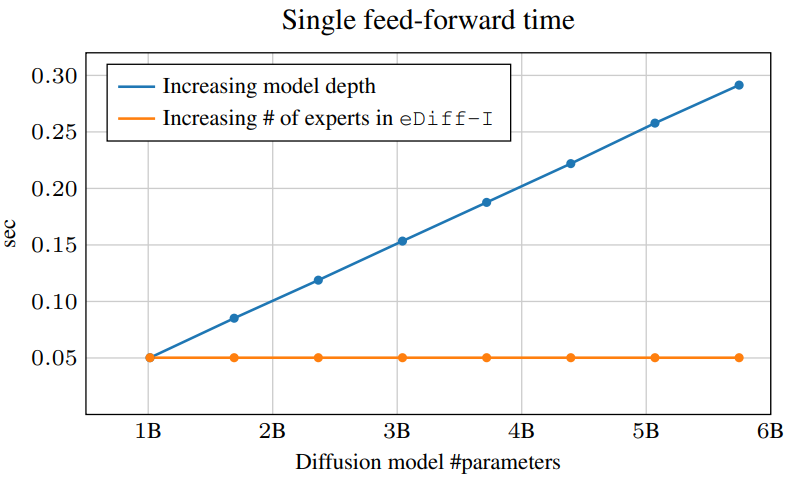
모델의 깊이를 증가시키는 경우 모델의 용량이 커지면 feed-forward 시간이 선형적으로 증가한다. 반면, eDiff-I의 경우 모델의 용량을 키워도 feed-forward 시간이 증가하지 않는다.

2. CLIP Text and T5 Text

다음은 텍스트 임베딩의 영향을 비교한 예시 샘플이다.

다음은 텍스트 임베딩의 영향을 비교한 그래프이다.

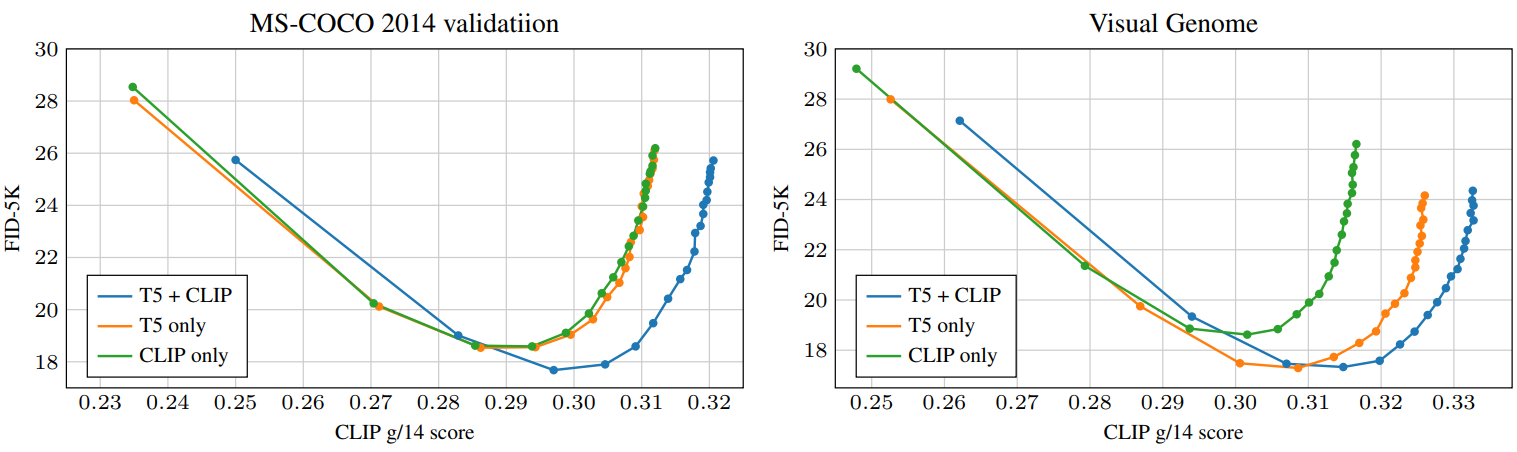
3. Style transfer

다음은 style transfer 결과들이다.

4. Paint-with-words

다음은 Paint-with-words로 생성한 결과들이다.