[논문리뷰] EdgeRunner: Auto-regressive Auto-encoder for Artistic Mesh Generation

arXiv 2024. [Paper] [Page]
Jiaxiang Tang, Zhaoshuo Li, Zekun Hao, Xian Liu, Gang Zeng, Ming-Yu Liu, Qinsheng Zhang
Peking University | NVIDIA Research
26 Sep 2024

Introduction

최근, 여러 접근 방식에서 메쉬를 1D 시퀀스로 토큰화하고 직접 메쉬 생성을 위해 auto-regressive model을 활용하려고 시도했다. 이러한 방법은 메쉬 vertex와 면에서 직접 학습하므로 토폴로지 정보를 보존하고 예술적인 메쉬를 생성할 수 있다. 그러나 이러한 auto-regressive한 메쉬 생성 방법은 여전히 ​​여러 가지 과제에 직면해 있다.

1. 많은 수의 면 생성: 비효율적인 면 토큰화 알고리즘으로 인해 대부분의 이전 방법은 1,600개 미만의 면이 있는 메쉬만 생성할 수 있으며, 이는 복잡한 물체를 표현하기에 충분하지 않다.
2. 고해상도 표면 생성: 이전 방법에서는 메쉬 vertex를 $128^3$ 해상도의 그리드로 quantize하여 상당한 정확도 손실과 매끄럽지 않은 표면이 발생한다.
3. 모델 일반화: 어려운 입력 모달리티를 가진 auto-regressive model을 학습시키는 것은 도전적인 일이다. 이전 방법은 단일 뷰 이미지를 조건으로 할 때 학습 도메인을 넘어 일반화하는 데 종종 어려움을 겪는다.

본 논문에서는 앞서 언급한 과제를 해결하기 위해 EdgeRunner라는 새로운 접근 방식을 제시하였다.

1. 시퀀스 길이를 50% 압축하고 토큰 간의 long-range dependency를 줄여 학습 효율성을 크게 개선하는 메쉬 토큰화 방법을 도입하였다.
2. 가변 길이의 삼각형 메쉬를 고정 길이의 latent code로 압축하는 Auto-regressive Auto-encoder (ArAE)를 제안하였다. 이 latent space는 다른 모달리티들로 컨디셔닝된 latent diffusion model을 학습시키는 데 사용할 수 있어 더 나은 일반화 능력을 제공한다.
3. 더 높은 quantization 해상도를 지원하기 위해 학습 파이프라인을 개선하였다.

이러한 개선 사항을 통해 EdgeRunner는 최대 4,000개의 면과 vertex를 $512^3$의 해상도로 discretize하여 다양하고 고품질의 메쉬를 생성할 수 있다. 이는 이전 방법에 비해 길이가 두 배, 해상도가 네 배 더 높은 시퀀스를 생성한다.

Method

1. Compact Mesh Tokenization

Auto-regressive model은 discrete한 토큰 시퀀스 형태로 정보를 처리한다. 따라서 컴팩트한 tokenization은 더 적은 토큰으로 정보를 정확하게 표현할 수 있기 때문에 매우 중요하다.

본 논문에서는 잘 확립된 삼각형 메쉬 압축 알고리즘인 EdgeBreaker를 기반으로 메쉬를 컴팩트하고 효율적으로 표현할 수 있는 tokenization 방식을 도입하였다. 메쉬 압축에 대한 핵심 통찰력은 인접한 삼각형 간의 edge 공유를 최대화하는 것이다. 이전 삼각형과 edge를 공유함으로써 다음 삼각형은 세 개의 vertex 대신 하나의 추가 vertex만 필요하다.

Half-edge

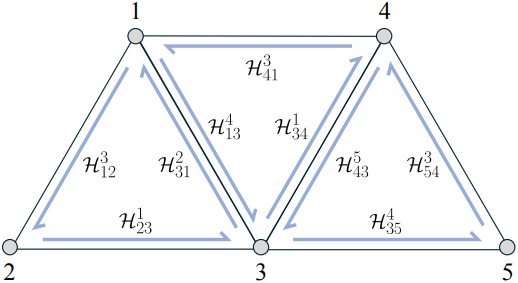
삼각형 면 순회를 위한 입력 메쉬를 표현하기 위해 half-edge 데이터 구조를 사용한다. Half-edge를 나타내기 위해 \(\mathcal{H}\)를 사용한다. 예를 들어, \(\mathcal{H}_{41}^3\)은 vertex 4에서 1을 가리키는 half-edge이며 면의 맞은편에는 vertex 3이 있다.

동일한 면 내에서 다음으로 이어지는 half-edge를 next half-edge라고 하며, 반대로 이전에 위치한 half-edge는 previous half-edge라고 한다. 또한, 동일한 edge를 공유한 half-edge는 twin half-edge라 부른다. 예를 들어, \(\mathcal{H}_{41}^3\)의 경우는 다음과 같다.

• next half-edge: \(\mathcal{H}_{13}^4\)
• next twin half-edge: \(\mathcal{H}_{31}^2\)
• previous half-edge: \(\mathcal{H}_{34}^1\)
• previous twin half-edge: \(\mathcal{H}_{43}^5\)

Vertex Tokenization

메쉬를 discrete한 시퀀스로 토큰화하려면 vertex 좌표에 discretization이 필요하다. MeshGPT를 따라 메쉬를 단위 큐브로 정규화하고 vertex 좌표를 quantization 해상도인 512에 따라 정수로 quantize한다. 따라서 각 vertex는 3개의 정수 좌표로 표현되고, 토큰으로 XYZ 순서로 flatten된다.

설명을 위해 개념을 약간 오용하여, 을 사용하여 XYZ 토큰을 하나의 vertex 토큰으로 표시하자.

Face Tokenization

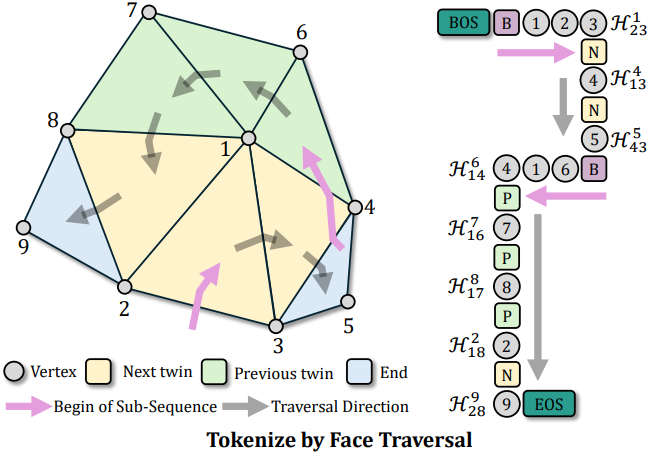
Half-edge를 따라 모든 면을 순회한다. 이 과정을 설명하기 위해 위 그림의 메쉬 예제를 사용하자. 이 과정은 하나의 half-edge에서 시작하며, 여기서 \(\mathcal{H}_{23}^1\)은 현재 순회의 시작으로 선택된다. 순회의 시작을 B로 표시하자. 그런 다음 half-edge 1에 vertex를 첫 번째 vertex 토큰으로 추가한다. 같은 삼각형 면 내에서 두 vertex 2 3도 \(\mathcal{H}_{23}^1\)의 방향을 따라 추가된다.

순회하는 동안 가능한 한 next twin half-edge를 방문하고 현재 순회에서 모든 삼각형을 소진했을 때만 half-edge 방향을 previous twin half-edge로 역전시킨다. 위의 예시로 돌아가면, \(\mathcal{H}_{23}^1\)을 따라가 \(\mathcal{H}_{13}^4\)에 도달한다. 따라서 다음 트윈 순회 방향을 나타내기 위해 N을 추가하고 1 3이 공유되므로 4만 추가하면 된다. 동일한 프로세스가 \(\mathcal{H}_{43}^5\)에 대해 반복되고 현재 sub-sequence에 N 5가 추가된다.

\(\mathcal{H}_{43}^5\)에 대해 인접한 면을 찾을 수 없으므로 현재 순회를 완료한다. 따라서 현재 순회의 sub-sequence는 B 1 2 3 N 4 N 5이다.

새로운 sub-sequence를 시작하기 위해, 마지막으로 추가된 half-edge를 역순으로 검색하여 반대 방향으로 순회한다. 마지막으로 추가된 half-edge \(\mathcal{H}_{43}^5\)에는 인접한 면이 없으므로, 그것을 건너뛰고 대신 \(\mathcal{H}_{13}^4\)을 고려한다. 따라서 \(\mathcal{H}_{13}^4\)의 previous twin half-edge인 \(\mathcal{H}_{14}^6\)로 이동한다. 이것은 새로운 sub-sequence이므로 B 6 1 4가 추가된다.

\(\mathcal{H}_{14}^6\) 근처에서 방문하지 않은 면을 계속 찾고 previous twin half-edge \(\mathcal{H}_{16}^7\)에 도착한다. 따라서 6 1이 공유되므로 현재 sub-sequence에 P 7을 추가한다. 프로세스가 반복되고 P 8 P 2 N 9가 추가된다. 모든 삼각형 면을 방문했으므로 메쉬의 face tokenization 프로세스가 완료된다.

보조 토큰

LLM과 마찬가지로, 메쉬 시퀀스의 앞에 BOS와 메쉬 시퀀스의 뒤에 EOS를 추가한다.

Detokenization

메쉬 토큰 시퀀스에서 원래 메쉬를 재구성하는 것은 간단하다. Sub-sequence의 각 B는 항상 세 개의 vertex 토큰이 뒤따른다. 각 N 또는 P는 하나의 vertex 토큰이 뒤따르고, 순회 방향을 기준으로 두 개의 이전 vertex 토큰을 검색하여 삼각형을 재구성한다. 마지막으로, 서로 다른 sub-sequence에서 여러 번 나타날 수 있으므로 중복된 vertex를 병합하고 재구성된 메쉬를 출력한다.

장점

본 논문의 tokenizer는 여러 가지 측면에서 모델 학습에 도움이 된다.

1. 각 면은 평균 4~5개의 토큰이 필요하여 이전 방법들에서 사용된 9개의 토큰과 비교하여 약 50%의 압축을 달성하였다. 이러한 향상된 효율성 덕분에 모델은 동일한 수의 토큰으로 더 많은 면을 생성할 수 있으며 더 많은 수의 면을 포함하는 데이터셋에 대한 학습이 용이해진다.
2. 순회는 토큰 간의 long-range dependency를 피하도록 설계되었다. 각 토큰이 이전 토큰의 짧은 컨텍스트에만 의존하도록 하여 학습의 어려움을 더욱 완화하였다.
3. 순회는 각 면의 방향이 각 하위 메쉬 내에서 일관되게 유지되도록 한다. 결과적으로 생성된 메쉬는 이전 방법에서는 일관되게 달성되지 않았던 back-face culling을 사용하여 정확하게 렌더링할 수 있다.

2. Auto-regressive Auto-encoder

비록 디코더가 auto-regressive하고 가변 길이의 토큰 시퀀스를 생성하지만, 생성 다양성과 컨디셔닝을 따르는 능력에 한계가 있다. 반면에, diffusion model은 이러한 한계를 해결하는 데 유망한 결과를 보여준다. Diffusion model을 적용하기 위한 핵심 과제는 고정 길이 데이터가 필요하다는 것이다. 메쉬 생성에는 가변 길이의 데이터 구조가 사용되고 삼각형 면의 수는 상당히 달라질 수 있다.

따라서 저자들은 가변 길이 메쉬를 고정 길이의 latent space로 인코딩하기 위한 Auto-regressive Auto-encoder (ArAE)를 제안하였다. 이는 latent diffusion model에서 VAE의 역할과 유사하다. ArAE 모델을 학습하기 위해 기하학적 정보에 대한 인코더 입력으로 포인트 클라우드가 선택되었고 출력으로 tokenize된 메쉬 시퀀스를 선택되었다. 따라서 ArAE 모델 자체도 포인트 클라우드를 조건으로 메쉬를 생성한다.

아키텍처

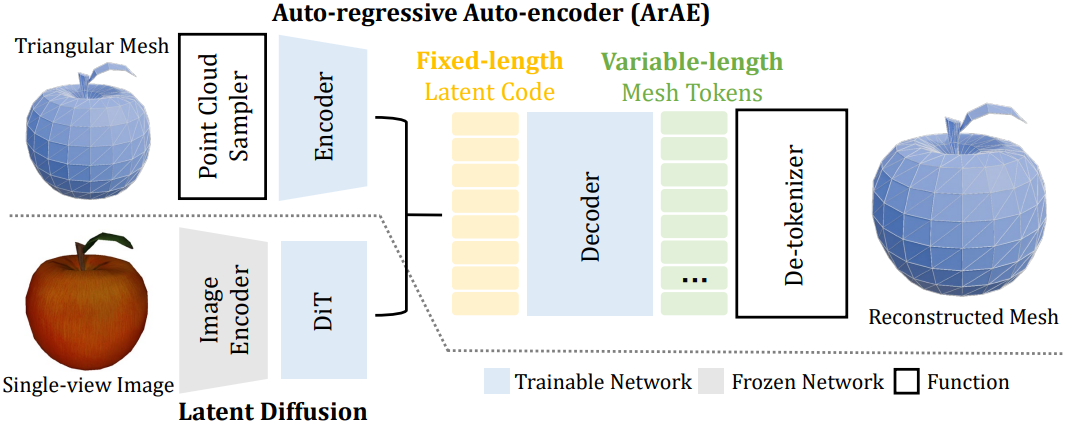
ArAE 모델의 아키텍처는 위 그림과 같다. ArAE는 가벼운 인코더와 auto-regressive 디코더로 구성되어 있다. 메쉬 표면에서 기하학적 정보를 추출하기 위해 포인트 클라우드를 샘플링하고 Transformer 인코더를 적용한다. 구체적으로, 입력 메쉬의 표면에서 $N$개의 랜덤 포인트 $\textbf{X} \in \mathbb{R}^{N \times 3}$을 샘플링하고 cross-attention layer를 사용하여 latent code를 추출한다.

\[\begin{equation} \textbf{Z} = \textrm{CrossAtt}(\textbf{Q}, \textrm{PosEmbed}(\textbf{X})) \end{equation}\]

여기서 $\textbf{Q} \in \mathbb{R}^{M \times C}$는 hidden dimension이 $C$인 학습 가능한 쿼리 임베딩, $\textrm{PosEmbed}(\cdot)$는 3D 포인트에 대한 frequency embedding function, $\textbf{Z} \in \mathbb{R}^{M \times L}$는 latent code이다. $M < N$은 latent 크기이고 $L < C$는 latent 차원이다.

디코더는 가변 길이의 메쉬 토큰 시퀀스를 생성하도록 설계된 auto-regressive Transformer이다. 단순화를 위해 OPT 아키텍처를 채택하였다. 학습 가능한 임베딩은 discrete한 토큰을 continuous한 feature로 변환하고 linear head는 예측된 feature를 classification logit으로 다시 매핑한다. 쌓여있는 causal self-attention layer들은 이전 토큰을 기반으로 다음 토큰을 예측하는 데 사용된다. Latent code $\textbf{Z}$는 입력 전에 BOS 토큰 앞에 추가되어 디코더가 latent code에 따라 메쉬 토큰 시퀀스를 생성하는 방법을 학습할 수 있도록 한다.

면 개수 조건

입력으로 포인트 클라우드 또는 단일 뷰 이미지가 주어지면 다양한 수의 면과 토폴로지를 가진 여러 개의 그럴듯한 메쉬를 생성할 수 있다. 면의 개수는 메쉬의 복잡성과 생성 속도에 직접적인 영향을 미치므로 특히 중요하다. 광범위한 면 개수를 가진 메쉬를 관리하기 위해 목표 면 개수에 대한 어느 정도의 명시적 제어를 제공해야 한다. 이 제어는 inference 중에 생성 시간과 생성된 메쉬의 복잡성을 추정하는 데 도움이 된다.

구체적으로, latent code 조건 토큰 뒤에 학습 가능한 면 개수 토큰을 추가한다. 면 개수를 다양한 범위로 구분하고, 각 범위에 서로 다른 토큰을 할당한다. 저자들은 1,000 이하, 1,000 ~ 2,000, 2,000 ~ 4,000, 4,000 초과에 각각 해당하는 4개의 개별 토큰을 사용하였다. 또한, 학습하는 동안 토큰을 무작위로 다섯 번째 unconditional 토큰으로 바꾼다. 이를 통해 모델이 목표 면 개수를 지정하지 않고도 메쉬를 생성하는 방법을 학습할 수 있도록 한다.

Loss Function

ArAE는 예측된 다음 토큰에 대한 cross-entropy loss를 사용하여 학습된다.

\[\begin{equation} \mathcal{L}_\textrm{ce} = \textrm{CrossEntropy} (\hat{\textbf{S}}[:-1], \textbf{S}[1:]) \end{equation}\]

여기서 $\textbf{S}$는 one-hot GT 토큰 시퀀스이고, \(\hat{\textbf{S}}\)는 예측된 분류 logit 시퀀스이다. 또한 latent space의 범위를 제한하여 diffusion model의 학습을 쉽게 만들기 위해 latent code에 L2 norm 페널티를 적용한다.

\[\begin{equation} \mathcal{L}_\textrm{reg} = \| \textbf{Z} \|_2^2 \end{equation}\]

최종 loss는 cross-entropy loss와 정규화 항의 조합이다.

3. Image-conditioned Latent Diffusion

ArAE 아키텍처가 제공하는 고정 길이의 latent space를 사용하면 2D 이미지 생성 모델이 학습되는 방식과 유사하게 다양한 입력으로 컨디셔닝된 메쉬 생성 모델을 학습시키는 것이 가능하다. 다양한 입력 모달리티 중에서 메쉬 생성에 가장 일반적으로 사용되는 조건 중 하나인 단일 뷰 이미지를 사용한다.

Backbone으로 diffusion transformer (DiT)를 활용한다. 구체적으로, CLIP의 이미지 인코더를 사용하여 컨디셔닝을 위한 이미지 feature를 추출한다. Cross-attention layer로 이미지 조건을 denoising feature에 통합하고, AdaLN 레이어로 timestep 정보를 통합한다.

저자들은 DDPM 프레임워크와 MSE loss를 사용하여 DiT 모델을 학습시켰다. 각 학습 step에서 timestep $t$와 Gaussian noise $\epsilon \in \mathbb{R}^{M \times L}$을 무작위로 샘플링한다. Loss는 예측된 noise와 $\epsilon$ 사이에서 계산된다.

Experiments

• Inference 속도
  • next-token prediction을 사용하므로 시퀀스의 길이에 따라 inference 시간이 달라짐
  • flash-attention과 KV cache를 적용
  • A100 GPU에서 초당 약 100 개의 토큰 생성
  • 면이 1,000개인 메쉬를 생성하는 데 45초 소요 (2,000개는 90초, 4,000개는 3분)

1. Qualitative Results

다음은 포인트 클라우드를 조건으로 생성한 메쉬를 비교한 것이다.

다음은 이미지를 조건으로 생성한 메쉬를 비교한 것이다.

다음은 면 개수를 대략적으로 조절하여 메쉬를 생성한 예시들이다.

2. Quantitative Results

다음은 tokenizer 알고리즘을 비교한 표이다.

3. Ablation Studies

다음은 (왼쪽) quantization 해상도와 (오른쪽) 이미지 컨디셔닝 전략에 대한 ablation 결과이다.