[논문리뷰] Easi3R: Estimating Disentangled Motion from DUSt3R Without Training

ICCV 2025. [Paper] [Page] [Github]
Xingyu Chen, Yue Chen, Yuliang Xiu, Andreas Geiger, Anpei Chen
Zhejiang University | Westlake University | Max Planck Institute for Intelligent Systems | University of Tübingen
31 Mar 2025

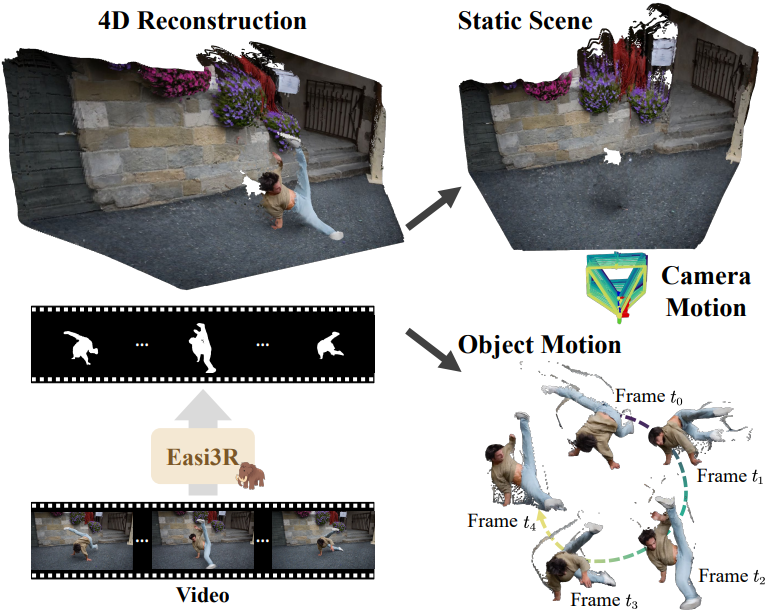
Introduction

정적 SfM과 동적 SfM 간의 정확도와 robustness 격차의 주요 원인은 실제 동영상에서 일반적인 물체의 움직임이다. 움직이는 물체는 기존 SfM 방법의 homography 및 epipolar 일관성의 기본 가정을 위반한다. 또한 카메라 모션과 물체 모션이 종종 얽히는 동적 동영상에서 이러한 방법은 두 모션을 분리하는 데 어려움을 겪으며, 종종 풍부한 텍스처를 가진 모션이 주로 카메라 포즈 추정에 잘못 기여하게 한다. MonST3R나 CUT3R와 같은 최근 방법들은 이러한 과제를 해결하기 위해 진전을 이루었지만, 이러한 성공은 광범위한 학습 데이터 또는 깊이, optical flow, object mask를 추정하는 task별 prior 모델에 기반한다.

인간은 신체 움직임과 장면의 구조를 인지하고, 동적인 물체를 식별하며, 뇌의 고유한 attention 메커니즘을 통해 자신의 움직임과 물체의 움직임을 구분할 수 있다. 그러나 학습 과정은 명시적인 동적 레이블에 의존하는 경우가 거의 없다.

저자들은 DUSt3R가 유사한 메커니즘을 암시적으로 학습했음을 관찰하였다. 이를 바탕으로 동적 동영상에서 동적 물체 segmentation, dense한 pointmap 재구성, robust한 카메라 포즈 추정을 달성하는 학습이 필요 없는 방법인 Easi3R를 소개한다. DUSt3R는 attention layer를 사용하여 두 개의 이미지 feature를 입력으로 받고 픽셀 정렬된 pointmap을 출력으로 생성한다. 이러한 attention layer는 레퍼런스 시점 좌표 공간에서 pointmap을 직접 예측하도록 학습되어 입력 시점 간의 이미지 feature를 암시적으로 매칭하고 feature space에서 시점 변환을 추정한다.

저자들이 transformer layer들의 attention map을 분석한 결과, 텍스처가 적고 관찰이 부족하며 동적 물체가 있는 영역은 낮은 attention 값을 생성할 수 있음을 발견했다. 따라서, 저자들은 구성 요소들을 분리하는 간단하면서도 효과적인 분해 전략을 제안하여 동적 물체 감지 및 segmentation을 가능하게 하였다. 이러한 segmentation을 통해 cross-attention layer에서 re-weighting을 적용하여 동적 데이터에 대한 fine-tuning 없이도 강력한 동적 4D 재구성 및 카메라 모션 복구가 가능하며, DUSt3R에 대한 추가 비용은 최소화된다.

Easi3R는 광범위한 데이터셋에서 놀라운 성능을 보이며, 동적 데이터셋에서 학습된 CUT3R, MonST3R, DAS3R보다 훨씬 뛰어나다.

Method

• 입력: 동영상 시퀀스 \(\{I^t \in \mathbb{R}^{W \times H \times 3}\}_{t=1}^T\)
• 출력: Segmentation \(\textbf{M}^t\), extrinsic \(\textbf{P}^t\), intrinsic \(\textbf{K}^t\), 포인트 클라우드 \(\mathcal{X}^\ast\)

1. DUSt3R with Dynamic Video

DUSt3R는 포즈가 필요 없는 재구성을 위해 설계되었으며, 두 개의 RGB 이미지 $I^a$와 $I^b$를 입력으로 받고 레퍼런스 뷰 좌표 공간에 있는 두 개의 pointmap을 출력한다.

\[\begin{equation} X^{a \rightarrow a}, X^{b \rightarrow a} = \textrm{DUSt3R} (I^a, I^b) \in \mathbb{R}^{W \times H \times 3} \end{equation}\]

(\(X^{b \rightarrow a}\)는 뷰 $a$의 좌표 공간에서 예측된 $I^b$의 pointmap)

멀티뷰 이미지가 주어지면, DUSt3R는 이미지를 쌍으로 처리하고, 모든 시점에 걸쳐 connectivity graph를 사용하여 쌍별 예측을 공동 좌표 공간에 글로벌하게 정렬한다. 그러나 이 접근법은 시점의 connectivity가 이미 알려져 있기 때문에 동영상 시퀀스에 대한 계산 중복성을 야기한다.

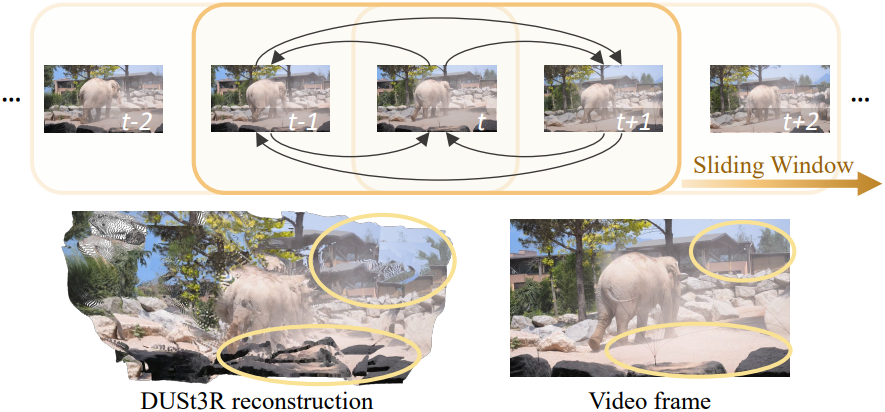
대신 저자들은 sliding temporal window를 사용하여 동영상을 처리하고, 시간 $t$를 중심으로 하는 크기 $n$의 대칭 window 내에서 쌍 집합

\[\begin{equation} \epsilon^t = \{(a, b) \, \vert \, a, b \in [t - \frac{n-1}{2}, \ldots, t + \frac{n-1}{2}], a \ne b\} \end{equation}\]

에 대하여 네트워크를 실행한다.

쌍별 예측을 통해 각 쌍의 좌표 공간에서 월드 좌표로의 변환 \(\textbf{P}_i^t \in \mathbb{R}^{3 \times 4}\)를 최적화하고 쌍 집합 \(\epsilon^t\) 내의 $i$번째 쌍에 대한 scale factor \(\textbf{s}_i^t\)를 사용하여 글로벌하게 정렬된 pointmap \(\{\mathcal{X}^t \in \mathbb{R}^{W \times H \times 3}\}_{t=1}^T\)을 복구한다.

\[\begin{equation} \mathcal{X}^\ast = \underset{\mathcal{X}, \textbf{P}, \textbf{s}}{\arg \min} \sum_{t \in T} \sum_{i \in \epsilon^t} \| \mathcal{X}^a - \textbf{s}_i^t \textbf{P}_i^t X^{a \rightarrow a} \|_1 + \| \mathcal{X}^b - \textbf{s}_i^t \textbf{P}_i^t X^{b \rightarrow a} \|_1 \end{equation}\]

위의 최적화 과정은 신뢰할 수 있는 쌍별 재구성을 가정하며, 위 식의 선형 방정식을 최소화함으로써 글로벌 콘텐츠를 정렬할 수 있다. 그러나 DUSt3R는 정적 장면의 RGB-D 이미지에서 학습되므로, 동적 물체는 학습된 epipolar matching 정책을 방해한다. 결과적으로 동적 콘텐츠가 픽셀의 상당 부분을 차지하면 정렬에 실패한다.

2. Secrets Behind DUSt3R

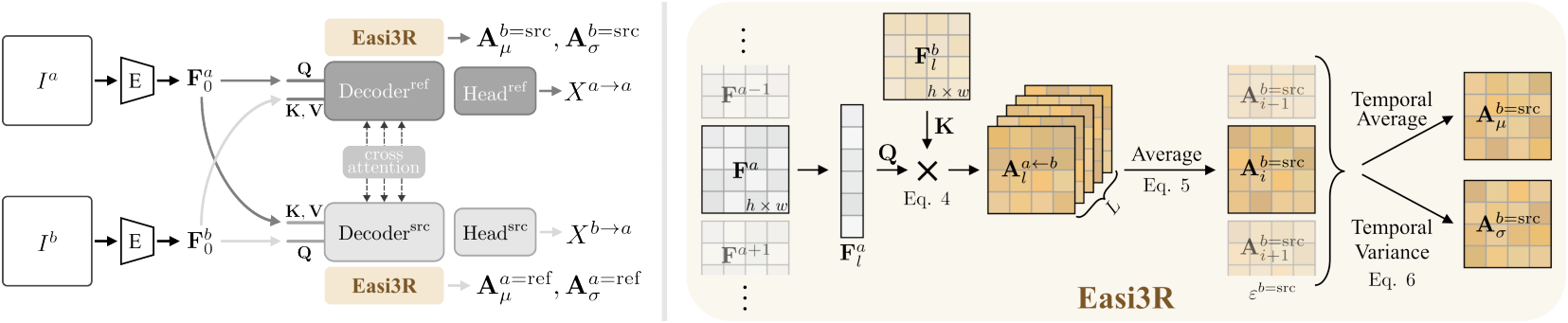
저자들은 동적 동영상 입력의 실패를 유발하는 구성 요소를 식별하기 위해 네트워크 아키텍처를 검토하였다. 위 그림에서 볼 수 있듯이, DUSt3R는 두 개의 branch로 구성된다. 위쪽 branch는 레퍼런스 이미지 $I^a$를 위한 것이고 아래쪽 branch는 소스 이미지 $I^b$를 위한 것이다. 두 입력 이미지는 먼저 공유 ViT 인코더에 의해 처리되어 토큰 표현 \(\textbf{F}_0^a\)와 \(\textbf{F}_0^b\)를 생성한다.

\[\begin{aligned} \textbf{F}_0^a &= \textrm{Encoder}(I^a) \\ \textbf{F}_0^b &= \textrm{Encoder}(I^b) \end{aligned}\]

다음으로, 디코더 블록 시퀀스로 구성된 두 개의 디코더는 뷰 내부 및 뷰 간에 정보를 교환한다. 각 블록에서 self-attention은 이전 블록의 토큰 출력에 적용되는 반면, cross-attention은 다른 branch의 해당 블록 출력을 사용하여 수행된다.

\[\begin{aligned} \textbf{F}_l^a &= \textrm{DecoderBlock}_l^\textrm{ref} (\textbf{F}_{l-1}^a, \textbf{F}_{l-1}^b) \\ \textbf{F}_l^b &= \textrm{DecoderBlock}_l^\textrm{src} (\textbf{F}_{l-1}^b, \textbf{F}_{l-1}^a) \end{aligned}\]

($l = 1, \ldots, L$은 블록 인덱스)

Feature 토큰을 사용하여 두 regression head는 pointmap 예측을 생성한다.

\[\begin{aligned} X^{a \rightarrow a} &= \textrm{Head}^\textrm{ref} (\textbf{F}_0^a, \ldots, \textbf{F}_L^a) \\ X^{b \rightarrow a} &= \textrm{Head}^\textrm{src} (\textbf{F}_0^b, \ldots, \textbf{F}_L^b) \\ \end{aligned}\]

블록은 예측된 pointmap과 GT pointmap 사이의 유클리드 거리를 최소화하여 학습된다.

Observation

저자들의 통찰력은 DUSt3R가 cross-attention layer를 통해 뷰 변환을 암시적으로 학습하여, 텍스처가 없는 영역, 관찰되지 않은 영역, 동적 영역과 같이 epipolar 제약 조건을 위반하는 토큰에 낮은 attention 값을 할당한다는 것이다. 저자들은 공간적 차원과 시간적 차원에 걸쳐 cross-attention 출력을 집계함으로써, attention layer에서의 동작을 추출하였다.

Spatial attention maps

이미지 feature $\textbf{F}$는 각각의 branch에 대한 query로 projection되며, 동시에 key와 value 역할도 한다.

\[\begin{equation} \textbf{Q} = \ell_\textbf{Q} (\textbf{F}) \in \mathbb{R}^{(h \times w) \times c}, \quad \textbf{K} = \ell_\textbf{K} (\textbf{F}) \in \mathbb{R}^{(h \times w) \times c}, \quad \textbf{V} = \ell_\textbf{V} (\textbf{F}) \in \mathbb{R}^{(h \times w) \times c} \end{equation}\]

($c$는 feature 차원)

이는 cross-attention map을 생성한다.

\[\begin{aligned} \textbf{A}_l^{a \leftarrow b} &= \frac{\textbf{Q}_l^a \textbf{K}_l^{b \top}}{\sqrt{c}} \in \mathbb{R}^{(h \times w) \times h \times w} \textbf{A}_l^{b \leftarrow a} &= \frac{\textbf{Q}_l^b \textbf{K}_l^{a \top}}{\sqrt{c}} \in \mathbb{R}^{(h \times w) \times h \times w} \end{aligned}\]

여기서 cross-attention map는 value $\textbf{V}$의 워핑을 가이드하는 데 사용되고, 레퍼런스 뷰 branch의 cross-attention 출력은 \(\textrm{softmax} (\textbf{A}_l^{a \leftarrow b}) \textbf{V}^b\)로 주어진다. 직관적으로, attention map \(\textbf{A}_l^{a \leftarrow b}\)은 $l$번째 디코더 블록에서 뷰 $b$에서 뷰 $a$로 정보가 어떻게 집계되는지를 결정한다.

뷰 $b$의 각 토큰이 뷰 $a$의 모든 토큰에 미치는 공간적 기여도를 평가하기 위해, query 차원과 layer 차원을 따라 서로 다른 토큰 간의 attention 값을 평균화한다.

\[\begin{aligned} \textbf{A}^{b = \textrm{src}} &= \sum_l \sum_x \textbf{A}_l^{a \leftarrow b} / (L \times h \times w) \in \mathbb{R}^{h \times w} \\ \textbf{A}^{a = \textrm{ref}} &= \sum_l \sum_x \textbf{A}_l^{b \leftarrow a} / (L \times h \times w) \in \mathbb{R}^{h \times w} \end{aligned}\]

평균화된 attention map \(\textbf{A}^{b = \textrm{src}}\)와 \(\textbf{A}^{a = \textrm{ref}}\)는 모든 디코더 layer에서 한 뷰에서 다른 뷰로의 토큰의 전반적인 영향을 포착한다. 즉, \(\textbf{A}^{b = \textrm{src}}\)는 소스 뷰로 사용될 때 뷰 $b$가 참조 뷰에 미치는 전반적인 기여도를 나타낸다.

Temporal attention maps

위의 단일 쌍 공식을 여러 쌍으로 확장하여 시간적인 attention 상관관계를 계산할 수 있다. 특정 프레임 $I^t$에 대해, 여러 프레임과 쌍을 이루어 프레임당 $2(n−1)$개의 attention map을 생성한다. 쌍별 cross-attention map을 시간적으로 집계하기 위해, 뷰가 소스와 레퍼런스로 사용하는 쌍에 대한 평균과 분산을 계산한다.

\[\begin{equation} \textbf{A}_\mu^{b = \textrm{src}} = \textrm{Mean} (\textbf{A}_i^{b = \textrm{src}}), \quad \textbf{A}_\sigma^{b = \textrm{src}} = \textrm{Std} (\textbf{A}_i^{b = \textrm{src}}) \\ \textrm{where} i \in \epsilon^{b = \textrm{src}} = \{(a, b) \, \vert \, \textrm{src} = b, a \in [t-n, \ldots, t+n], a \ne b\} \end{equation}\]

마찬가지로, 뷰 $a$가 소스 뷰 역할을 하는 쌍 집합

\[\begin{equation} \epsilon^{b = \textrm{ref}} = \{(b, a) \, \vert \, \textrm{ref} = b, a \in [t-n, \ldots, t+n], a \ne b\} \end{equation}\]

에 대해 \(\textbf{A}_\mu^{b = \textrm{ref}}\)와 \(\textbf{A}_\sigma^{b = \textrm{ref}}\)를 계산한다.

Secrets

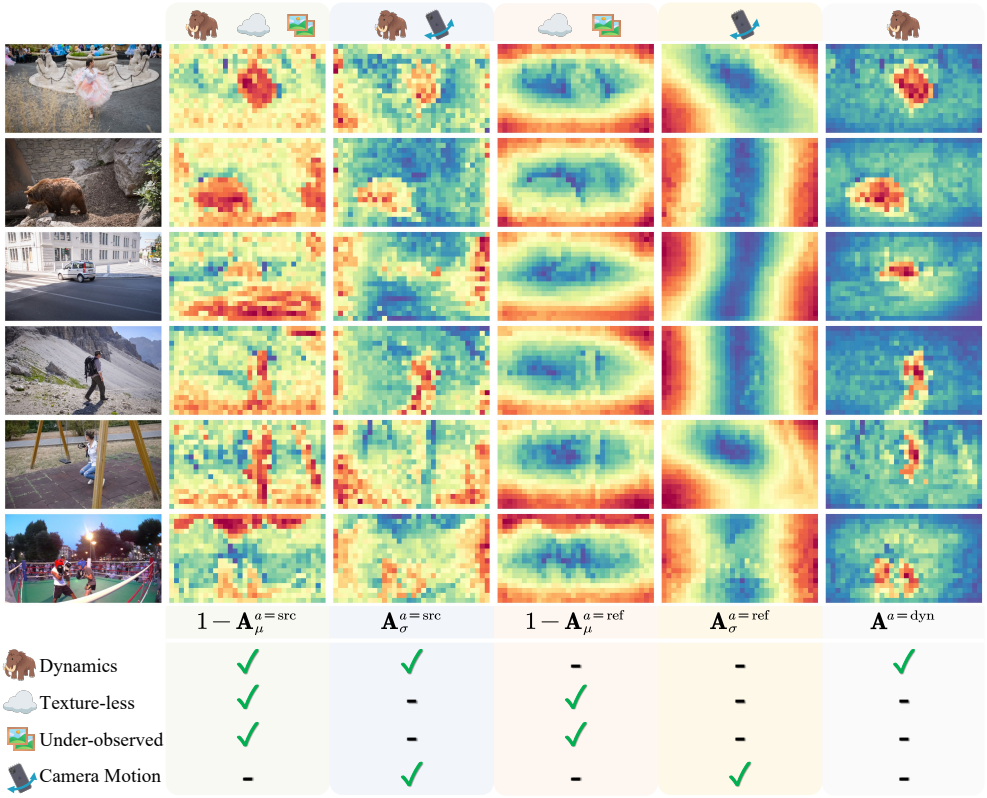
위 그림은 집계된 temporal cross-attention map을 시각화한 것이다. DUSt3R는 레퍼런스 뷰 좌표 프레임의 두 이미지에서 pointmap을 추론하여 소스 뷰에서 레퍼런스 뷰로 포인트를 암시적으로 정렬한다.

레퍼런스 뷰는 정렬 기준으로 사용되며 정적이라고 가정된다. 결과적으로 평균 attention map \(\textbf{A}_\mu^{a = \textrm{ref}}\)는 매끄러워지는 경향이 있으며, 텍스처가 없는 영역과 관찰되지 않은 영역은 자연스럽게 낮은 attention 값을 보이는데, 이는 DUSt3R가 이러한 영역이 정렬에 덜 유용하다고 판단하기 때문이다. 이러한 영역은 \((1 − \textbf{A}_\mu^{a = \textrm{ref}})\)를 사용하여 추출할 수 있다.

\(\textbf{A}_\sigma^{a = \textrm{ref}}\)를 계산하면 이미지 좌표 공간에서 토큰 기여도의 변화를 얻을 수 있다. 움직임 방향에 수직인 픽셀은 일반적으로 유사한 pixel flow 속도를 공유하여 일관된 편차를 발생시키고, 이를 통해 attention 패턴에서 카메라 움직임을 추론할 수 있다.

\((1 - \textbf{A}_\mu^{a = \textrm{src}})\)를 계산하면, 텍스처가 적고 적게 관찰된 영역을 나타낸다. 또한, 동적 물체는 DUSt3R가 3D 데이터셋에서 학습한 시점 변환 prior를 위반하기 때문에 \(\textbf{A}_\mu^{a = \textrm{src}}\)가 낮아 \((1 - \textbf{A}_\mu^{a = \textrm{src}})\)가 강조된다.

\(\textbf{A}_\sigma^{a = \textrm{src}}\)를 계산하면 카메라의 움직임과 물체의 움직임을 모두 강조하는데, 이 영역의 attention은 시간에 따라 지속적으로 변하기 때문에 이미지 공간에서 높은 편차가 발생하기 때문이다.

3. Dynamic Object Segmentation

저자들은 도출된 cross-attention map의 특성을 관찰함으로써, 동적 물체 segmentation을 추출하는 것을 제안하였다. 이를 위해 물체 움직임에 기인하는 attention activation을 식별하고 element-wise product를 사용하여 동적 attention map을 추론하였다.

\[\begin{equation} \textbf{A}^{a = \textrm{dyn}} = (1 - \textbf{A}_\mu^{a = \textrm{src}}) \cdot \textbf{A}_\sigma^{a = \textrm{src}} \cdot \textbf{A}_\mu^{a = \textrm{ref}} \cdot (1 - \textbf{A}_\sigma^{a = \textrm{ref}}) \end{equation}\]

그런 다음, 미리 정의된 attention threshold $\alpha$를 사용하여 프레임별 동적 물체 segmentation $\textbf{M}^t$를 얻는다.

\[\begin{equation} \textbf{M}^t = \unicode{x1D7D9} [\textbf{A}^{t = \textrm{dyn}} > \alpha] \end{equation}\]

Segmentation은 프레임별로 처리되며, 저자들은 시간적 일관성을 높이기 위해 모든 프레임의 정보를 융합하는 feature 클러스터링 방법을 적용하였다.

4. 4D Reconstruction

정적 모델을 동적 장면에 적응시키는 가장 직관적인 방법은 이미지와 토큰 레벨 모두에서 동적 물체를 마스킹하는 것이다. 이는 이미지에서 동적 영역을 검은색 픽셀로 대체하고, 해당 토큰을 마스크 토큰으로 대체함으로써 가능하다. 실제로 이러한 방식은 재구성 성능을 크게 저하시키는데, 이는 검은색 픽셀과 마스크 토큰이 분포 범위를 벗어난 입력을 생성하기 때문이다. 따라서 입력 이미지를 수정하는 대신 attention layer 내에서 직접 마스킹을 적용하는 것이 바람직하다.

Attention re-weighting

저자들은 동적 영역과 관련된 attention 값을 약화시켜 cross-attention map을 수정하는 방안을 제안하였다. 이를 위해 네트워크에 두 번째 inference pass를 수행하여 할당된 동적 영역에 대한 attention map을 마스킹한다. 이렇게 하면 해당 영역에 대한 attention은 0이 되고 나머지 attention map은 그대로 유지된다.

\[\begin{equation} \textrm{softmax}(\tilde{\textbf{A}}_l^{a \leftarrow b}) = \begin{cases} 0 & \textrm{if} \; \textbf{M}^{a \leftarrow b} \\ \textrm{softmax} (\textbf{A}_l^{a \leftarrow b}) & \textrm{otherwise} \end{cases} \\ \textrm{where} \quad \textbf{M}^{a \rightarrow b} = (1 - \textbf{M}^a) \otimes \textbf{M}^{b \top} \in \mathbb{R}^{(h \times w) \times (h \times w)} \end{equation}\]

($\otimes$는 외적)

이로 인해 뷰 $b$의 동적 영역에서 나온 토큰이 뷰 $a$의 정적 영역에는 영향을 미치지 않는다. 소스 뷰는 정적 레퍼런스 뷰를 필요로 하므로 re-weighting은 레퍼런스 뷰 디코더에만 적용된다. 이를 위해 소스 뷰 디코더는 레퍼런스 뷰의 모든 토큰에 대해 cross-attention을 수행해야 한다. 두 가지 branch 모두에 동적 attention을 re-weighting하면 정적인 표준이 손실되어 노이즈가 있는 출력이 생성될 수 있다.

Global alignment

Sliding window에서 예측된 pointmap을 글로벌 월드 좌표에 정렬한다. 또한 동적 영역 segmentation 덕분에 optical flow와 함께 segmentation 기반의 글로벌 정렬을 사용할 수 있다. 특히, projection된 point flow가 optical flow와 일관성을 유지하도록 reprojection loss를 통합한다.

구체적으로, 이미지 쌍 $(a, b)$가 주어지면 글로벌 pointmap \(\mathcal{X}^b\)를 카메라 $(\textbf{P}^a, \textbf{K}^a)$에서 카메라 $(\textbf{P}^b, \textbf{K}^b)$로 projection하여 프레임 $a$에서 프레임 $b$로의 카메라 모션 \(\hat{\mathcal{F}}^{a \rightarrow b}\)를 계산한다. 그런 다음, 계산된 flow와 추정된 optical flow \(\mathcal{F}^{a \rightarrow b}\) 간의 일관성을 정적 영역 $(1 - \textbf{M}^t)$에 대하여 적용한다.

\[\begin{equation} \mathcal{L}_\textrm{flow} = \sum_{t \in T} \sum_{i \in \epsilon^t} (1 - \textbf{M}^a) \cdot \| \hat{\mathcal{F}}_i^{a \rightarrow b} - \mathcal{F}_i^{a \rightarrow b} \|_1 + (1 - \mathbb{M}^b) \cdot \| \hat{\mathcal{F}}_i^{b \rightarrow a} - \mathcal{F}_i^{b \rightarrow a} \|_1 \end{equation}\]

최적화 과정에 flow 제약 조건을 포함함으로써 글로벌 pointmap \(\mathcal{X}^\ast\)와 포즈 시퀀스 \(\textbf{P}^t\), \(\textbf{K}^t\)에 대해 더욱 robust한 출력을 얻을 수 있다.

Experiments

1. Dynamic Object Motion

다음은 동적 물체 segmentation에 대한 성능을 비교한 결과이다.

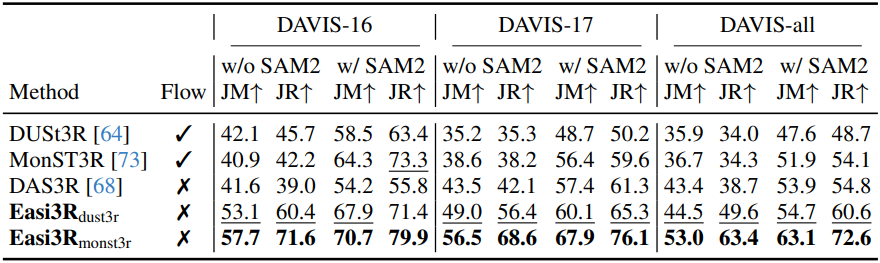
2. Camera Motion

다음은 카메라 포즈 추정 성능을 비교한 결과이다.

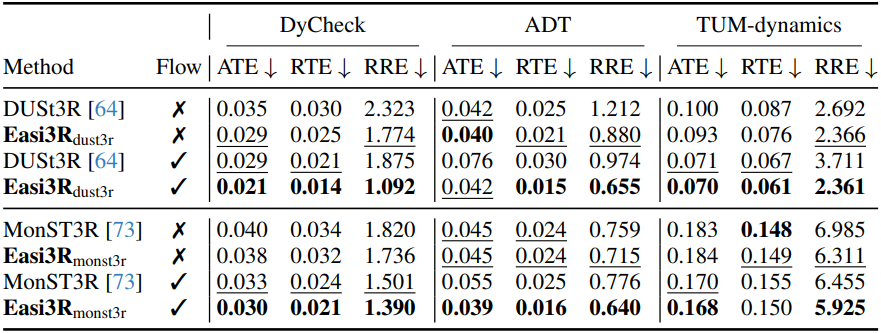
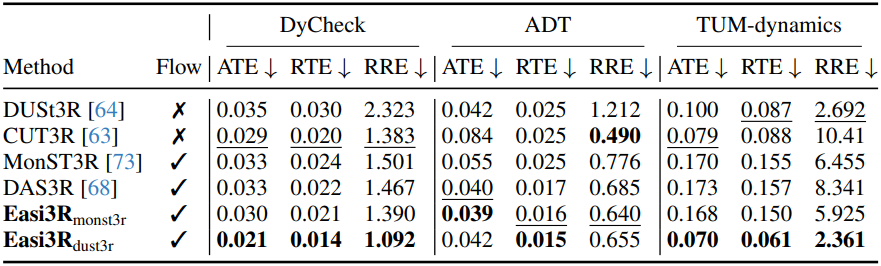
다음은 추정된 카메라 궤적을 시각화하여 비교한 예시이다.

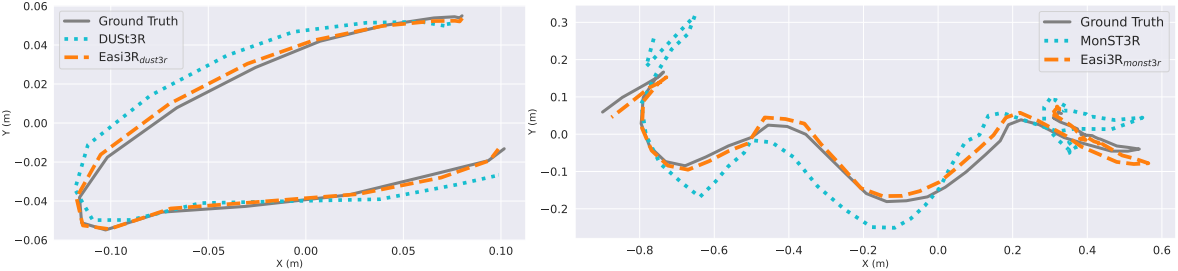
3. 4D Reconstruction

다음은 포인트 클라우드 재구성 성능을 비교한 결과이다.

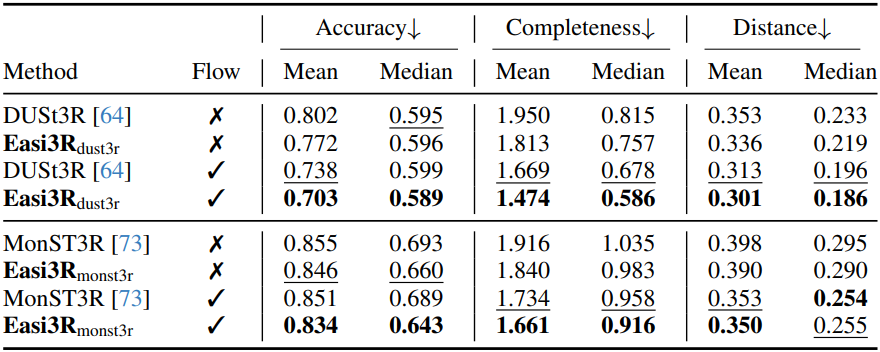
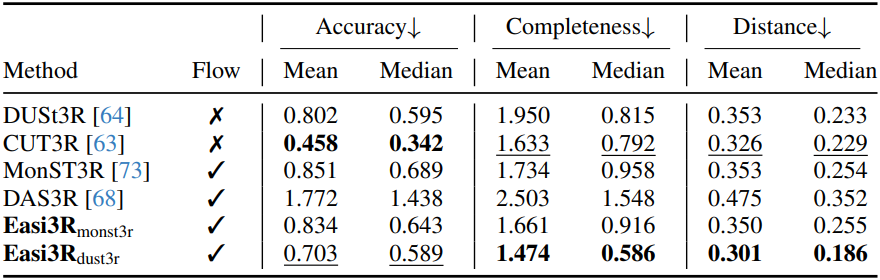
다음은 글로벌하게 정렬된 정적 장면과 특정 타임스탬프의 동적 포인트 클라우드를 동시에 시각화하여 비교한 예시이다.